Generalized heat diffusion equations with variable coefficients and their fractalization from the Black-Scholes equation
Rami Ahmad El-Nabulsi and Alireza Khalili Golmankhaneh
1 Biomedical Device Innovation Center,Shenzhen Technology University,3002 Lantian Road,Pingshan District,Shenzhen,518118,China
2 Research Center for Quantum Technology,Faculty of Science,Chiang Mai University,Chiang Mai,50200,Thailand
3 Athens Institute for Education and Research,Mathematics and Physics Divisions,8 Valaoritou Street,Kolonaki,10671,Athens,Greece
4 Department of Physics,Urmia Branch,Islamic Azad University,Urmia,Iran
Abstract In this study,we prove that modified diffusion equations,including the generalized Burgers’equation with variable coefficients,can be derived from the Black-Scholes equation with a timedependent parameter based on the propagator method known in quantum and statistical physics.The extension for the case of a local fractal derivative is also addressed and analyzed.
Keywords: Black-Scholes equation,heat kernels,modified diffusion equations,generalized Burger’s equation,fractal calculus
1.Introduction
The well-known Black-Scholes model (BSM) based on the diffusion process called geometric Brownian motion provides a closed form for the values of certain options such as the European put options [1].This model has a broad range of applications ranging from finance to statistical physics,mainly in the theory of anomalous diffusion processes(see[2]and references therein).The theoretical results predicted by the model are not ideal and do not completely agree with real-world applications.Given that the BSM is not satisfactory for calibrating market option data,time-dependent volatility has been conjectured by several studies.In addition,the BSM with time-varying parameters plays a crucial role in quantitative finance,since timedependent volatility influences investment expectations.Many attempts have been made to construct a viable BS model with a time-dependent volatility function,using the BS equation with variable volatility [2,3].Although the BSM has largely been used with constant volatility in physical systems exhibiting diffusion and anomalous diffusion behaviors,the implications of variable volatility are,to the best of our knowledge,absent from the theory of diffusion.This study aims to show that,under simple coordinate transformation,the generalized Burgers’equation which occurs in various areas of applied sciences such as fluid dynamics and gas dynamics may be derived from the Black-Scholes equation(BSE)with time-dependent coefficients.Moreover,due to the importance of fractals in diffusion processes,finance,and economics,where multifractality,heavytailed probability distributions,and volatility clustering play important roles[4-26],we will extend our approach to the case of fractal calculus which is an important investigation approach.Fractal calculus is a recent mathematical field of study.Due to its universality,this approach is not effectively used in the field of finance and partial differential equations.In general,fractals are non-differentiable irregular shapes used in several financial studies such as market prices [27-29].Recently,Fα-calculus,which is a particular branch of fractal calculus,was formulated in a seminal paper by A.D.Gangal and co-authors[38,30-37].The advantages of fractal calculus are that it is algorithmic,simple,local,and conjugate with ordinary calculus [30,31].
This study is organized as follows: in section 2,we introduce the basic setups of our approach; in section 3,the main results were discussed and analyzed; in section 4,a reformulation of the current approach using fractal calculus is introduced,analyzed,and discussed; finally conclusions are given in section 5.
2.Basic setup
In the framework of the BS model,given a continuous function f(t,S(t)) where(S,t) ∈ R+×[0 ,T),the following modified Taylor expansion holds:

Here,ε is a elementary time which the series expansion of f(t,S(t)) is performed around,as follows:

S(t) is the option of an underlying security which is assumed to be a stochastic variable and which is governed by the stochastic Langevin or Ito-Weiner equation:

Here,φ(t) is the expected return on the security S(t),σ(t) its volatility(assumed to be time-dependent),and Rtis the usual Gaussian white noise with a zero mean and which satisfies=δ(t-t′)(a delta function correlator) [3].If we discretize the time as t=nε,the probability distribution function of white noise is then given by:withand accordingly:

therefore,for ε →0,we can write equation (1) as:

This equation can be also obtained using Ito’s calculus.In the BS model,the delta-hedge (self-financing and riskless) portfolio is defined by:Sand subsequently,the rate of return is given by:

On the other hand,since the gain in the value of the portfolio π is deterministic,cannot be more or less than the gain in the value of the portfolio invested at the risk-free interest rate r(assumed to be time-dependent).Therefore=rπand after dropping the φ term (bearing in mind that the pricing of the security derivative is based on a risk-neutral process which is independent of the investor’s opinion),we can write:

This problem is,in general,associated with the initial conditions:

and the boundary conditions:

Here,f(S,t)→S as S →∞,where f(S,T) is defined over 0 <S <∞,0 <t <T.The call option gives the payoff max(ST-K,0)at a future time T.The accessible literature has largely treated the boundary conditions for the pricing equations(see [39] and references therein)
3.Main Results
By performing a change of variable R(t)=t-αr(t),α ∈R which is the time-dependent effective risk-free interest rate,equation (7) is effortlessly reduced to:
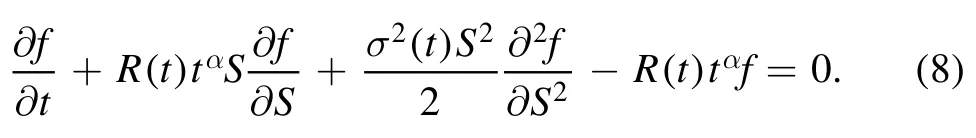
It is notable that the time-dependent parameters in financial dynamics have largely been addressed in the literature through different aspects and methodologies[40-49].Letting x=lnS and introducing the new variable τ=T-t (the time to expiry,such that τ=0 at T=t),it is easy to check that equation (8) turns into:

Setting
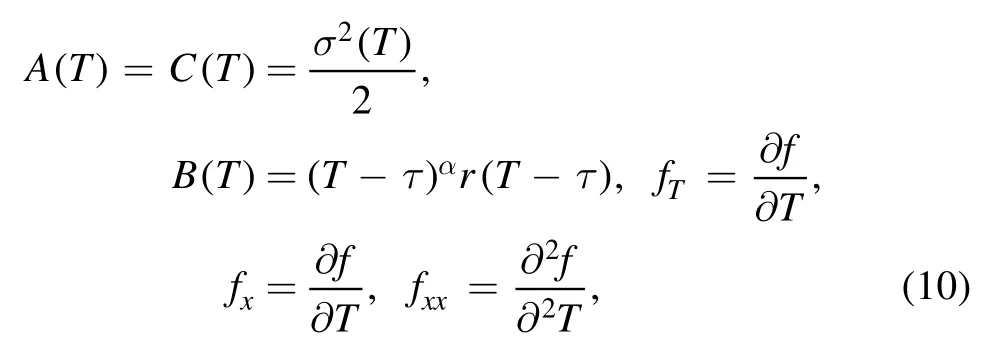
we can write equation (9) as:

Eq.(11) describes a financial model with a time-dependent effective risk and a time-dependent volatility.The solution is given by(for the details of calculations and derivations of the solution,please refer to [48,49]):

where:
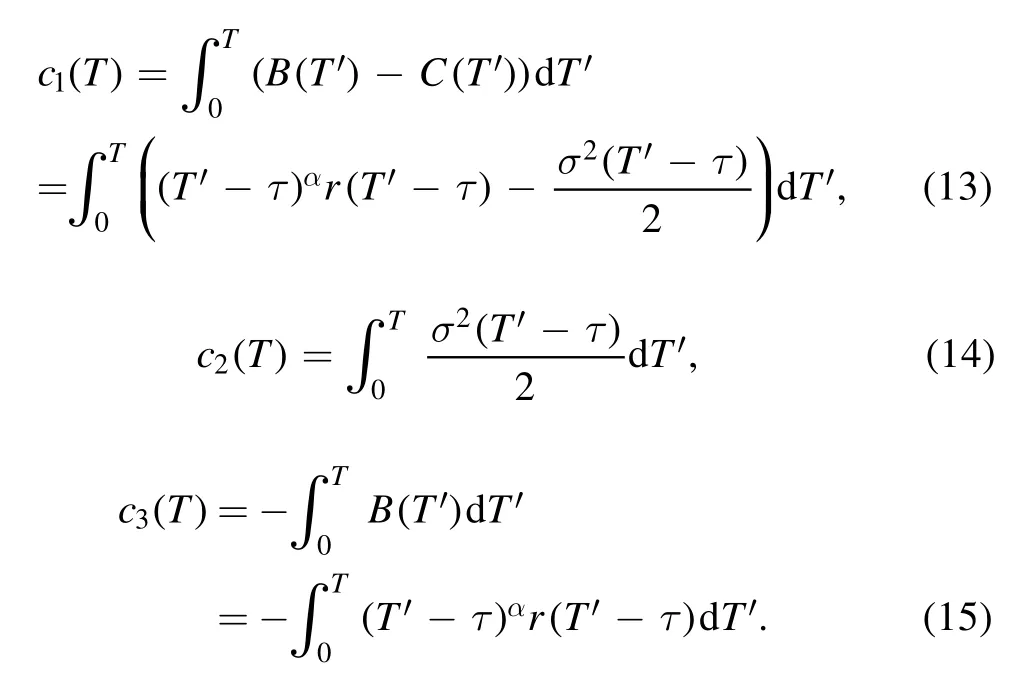
Since scaling behavior and power laws are common features and ubiquitous in finance and macroeconomics [50-55],we assume throughout this work that both volatility and risk vary as power laws.We propose the following scaling relations:

If β and χ have positive values,then it is obvious that both the (risk-free) interest rate and the volatility grow with time.However,in some cases,the interest rate may decrease over time.On the other hand,the justification for these expressions is related to the ubiquity of power laws in finance.Therefore,we obtain:

Using the following mathematical relations [48,49]:


whereG(x,t;x′ ,0) is the propagator of the pricing equation.For 0 <α ≤1 and τ=T-t <<1 (in normalized units),we can approximate equation (23) by:

If χ <2α-3,which corresponds for the special case of a perturbed risk-free interest rate returning to its equilibrium rate in power-law decay,we can reduce equation (24) to:

where

is the effective heat kernel.For= 2,equation (26) solves the following modified heat diffusion equation [56]:

which is reduced to its standard form for r1=0.Equation(27)is comparable to the generalized Burgers’ equation with variable coefficients [57] of the form:

where f(T) and g(T) are arbitrary smooth functions.It can be proved that equation(28)may be reduced via a change of the variable T to the well-known variable coefficient generalized Burgers’ equations with linear damping of the form [58,59]:

Figure 1.The Cantor set,the staircase function,and the solution of the fractal Black-Scholes equation.

where g(T) is another arbitrary smooth function.However,for:and χ=-α,equation (25) is reduced,for large T,to:

which solve the following modified heat diffusion equation:

More generally,the effective heat kernel associated with equation (26) solves a nonlinear heat equation.
4.Fractal Black-Scholes equation with timedependent parameters
The aim of this section to generalize the outcomes of the previous section by involving fractal derivatives and time[60,62,63,61].We start by reviewing the basic concepts of fractal calculus.Fractal calculus is a recently formulated framework that includes the derivatives and integrals of functions within a fractal domain[30-34].If F is a thin Cantor set,then the Fαderivative of (h)t:F→ R at t is defined by[30-34]

In figures 1(a),(b),(c),and (d) we have plotted the thin Cantor set,the staircase function,and equation (58),respectively.

Figure 2.Graphs corresponding to equation (58).
Let h(t,Q(t));F×R+→R.Using a fractal Taylor expansion,we have:

The analog of equation (3) is given by

where Ptis fractal Gaussian white noise with a correlation function,as follows:

where

Fractalizing equation (4) gives the following equation

Also,the fractal version of equation (5) becomes:
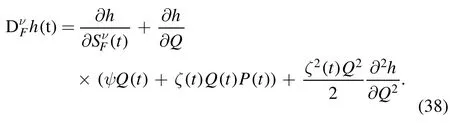
Fractalizing equation (7) leads to


By the same assumption as that given in the previous section,we can write the fractal version of equation (9) as follows:

The solution of equation (41) is

where

and

By fractalizing equations (16) and (17),we arrive at

Using equations (46) and (47),we obtain
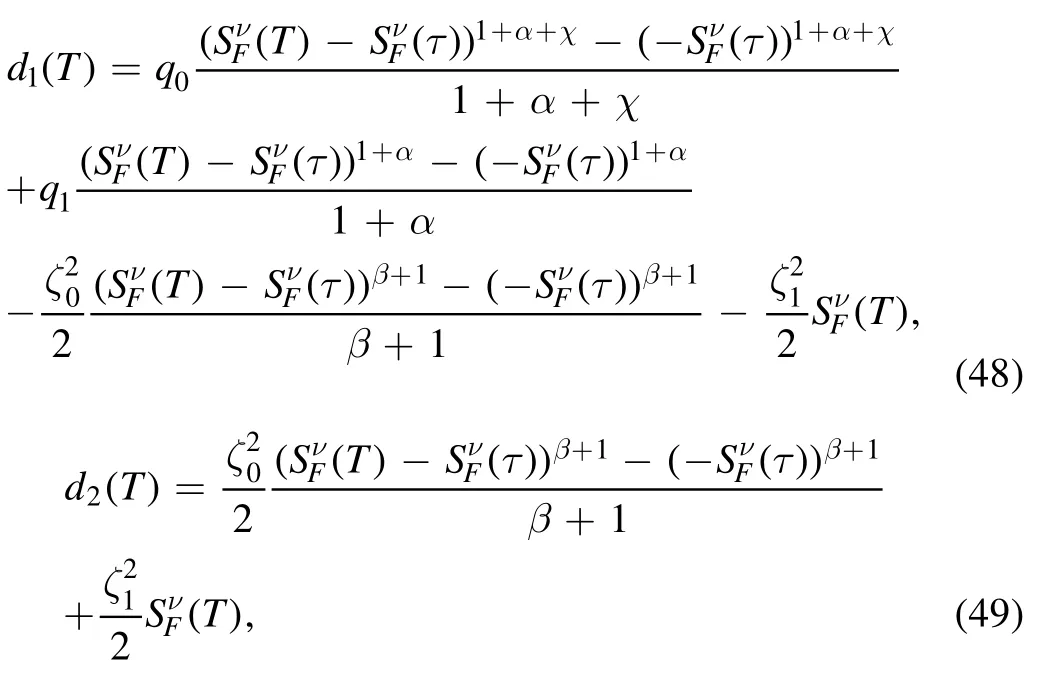
and

We conclude that

where

Similar arguments using fractal calculus give an analog of equation (27),as follows:

Following the same assumption as that given for equation (28),we obtain

If h(T)=1 then we have

Using the same assumptions for equation (30),we get

where,if we chooseh(x′,0) =x′,it follows that
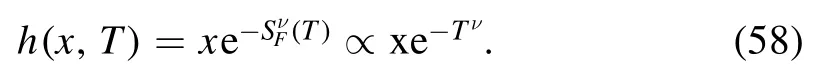
In figure 2,we have plotted equation (58) for different values of ν,where the case ν=1 gives the graph for equation(30)with the conditionh(x′,0) =x′.Equation(56)is the solution of the following fractal-modified heat diffusion:

We wish to stress that the dissimilarities between the graphs in figures 2(b),(d),and(f)for different values of ν are due to the tails of function f,which demonstrate the presence of the anomalous diffusion processes normally found in financial market dynamics.
Remark 1.Note that all the previous equations and results can be reduced to those obtained in sections 2,and 3 by choosing ν=1.
Although the fractal Burgers’ equation has largely been addressed in the literature [64-67],the methodology presented in this study based on local fractal calculus is not complicated,compared to the methodologies addressed in the literature,which are based on fractional calculus and higherorder derivatives[68-79].Moreover,the generalized Burgers equations obtained in both approaches discussed throughout this study are simpler than those addressed in the literature which use various complicated tools such as ultrafunctions[80] and the generalized ultrafunction solution [81] among others [82].We argue that the methodologies addressed in this study may be also used to derive various generalized partial differential equations that may have important implications in various fields of study.
5.Conclusions
The BSE is one of the most important partial differential equations used in finance and economics studies.However,empirical studies show that several properties of markets cannot be correctly modeled by the conventional BS model.Therefore,in recent years,many generalizations of the BS model based on the concept of BSE with time-dependent parameters have been addressed in the literature.In this paper,we considered a BSE with time-dependent volatility and we proved that a family of modified diffusion equations including the generalized Burgers’ equation with variable coefficients may be obtained accordingly.Our methodologies are based on the notion of Feynman’s propagator,which is well-known in statistical and quantum physics.We focused on power-law volatility and risk which are the main scaling features in financial market fluctuations.We also extended this approach to the case of a local fractal derivative due to the importance of fractal calculus in financial theories and diffusion processes.A fractal generalized Burgers’ equation was derived,which differed from the fractal equations obtained in literature by its simplicity.We argue that such a technique may be useful in the derivation of dissimilar partial differential equations,which could have several implications for applied sciences and financial markets [83].Work is in progress towards this end.
Acknowledgments
The authors would like to thank the anonymous referees for their useful comments and valuable suggestions.
ORCID iDs
Alireza Khalili Golmankhanehhttps://orcid.org/0000-0002-5008-0163
 Communications in Theoretical Physics2021年5期
Communications in Theoretical Physics2021年5期
- Communications in Theoretical Physics的其它文章
- Insight into the chemomechanical coupling mechanism of kinesin molecular motors
- A pedagogical review on solvable irrelevant deformations of 2D quantum field theory
- Ab initio study of the effects of helium on the mechanical properties of different erbium hydrides
- Interface water-induced hydrophobic carbon chain unfolding in water
- A simplified Parisi ansatz
- Vector kink-dark complex solitons in a threecomponent Bose-Einstein condensate
