General -lumps,-breathers,and hybrid solutions to(2+1)-dimensional generalized KDKK equation?
Peisen Yuan(袁培森), Jiaxin Qi(齊家馨), Ziliang Li(李子良), and Hongli An(安紅利),?
1College of Artificial Intelligence,Nanjing Agricultural University,Nanjing 210095,China
2College of Oceanic and Atmospheric Sciences,Ocean University of China,Qingdao 266100,China
3College of Sciences,Nanjing Agricultural University,Nanjing 210095,China
Keywords: KDKK equation, Hirota bilinear method, high-order lump solution, T-breather solution, hybrid solution
1. Introduction
Exact solutions of nonlinear equations are very important. Not only because exact solutions can help us to obtain some useful physical information hidden in the model, but also because they can work as benchmarks to test and improve numerical algorithms, which may lead to some deeper applications.[1]Therefore, many experts have devoted themselves to constructing exact solutions of nonlinear equations and lots of effective methods have been proposed, including the inverse scattering theory, B¨acklund transformation, Darboux transformation, Wronskian and Casoratian techniques,variable separation approach, Hirota bilinear method, and so on.[2–17]
Among the above methods,the Hirota bilinear method is more popularly used to construct N-soliton solutions,breather and lump solutions of nonlinear equations due to its directness and simplicity. Solitons are stable waves. Breathers are partially localized on a background and periodic in a certain direction. While, lumps are localized in all directions in the space. Such lump solutions have been considered as perfect prototypes for explaining rogue wave dynamics in financial crisis, nonlinear optics, plasmas, oceanography, and Bose–Einstein condensates.[18–21]In recent years, the researches on the breather and lump solutions as well as their interactions have been a hot topic in physical areas and many results have been achieved. For example, Yue et al. derived N solitons, breather, and lump solutions of the nonlinear evolution equation.[22]Wang et al. obtained breather solutions of the Ito equation and analyzed their dynamics.[23]Liu et al.derived the breathers, lumps, and interaction solutions of the KP equation.[24]Zhang and Ma presented a class of lump solution of the (2+1)-dimensional SK equation via the generalized bilinear forms.[25]Zhang et al. gave the breather and lump solutions for the nonlocal KP equation,[26]and Yong et al., based on symbolic computation, derived the lump solutions for the KPI equation.[27]Huang et al. investigated interaction solutions between kink soliton solutions and lumps of the generalized KP equation.[28]Wang and Zhang obtained some lump solutions for a reduced Hirota equation.[29]Ma and his coworkers computed lumps solutions for two combined fourth-order soliton equations[30,31]and nonlinear dispersive waves with higher-order dispersion relations.[32]And they showed that such lumps solutions had rich dynamical behaviors. Meanwhile,there is also some work on breather and lump solutions of other nonlinear equations.[33–38]However,we find that most work mentioned above only focuses on the low-order lump and breather solution.For the high-order solutions of breathers,lumps and their interactions,little work has been done due to the difficulty in selecting suitable parameters involved in N-solitons. However, such high-order breathers,lumps as well as the interaction solutions, compared with the corresponding 1-lump and 1-breather, have more importance and wide applications in real world. Therefore,it is worthy of studying the high-order breather,lump solutions,and interactions of nonlinear equations.
As analyzed above, in the present work we shall investigate higher-order breathers, lumps, and their interactions for the (2+1)-dimensional generalized KDKK equation, which takes a form of
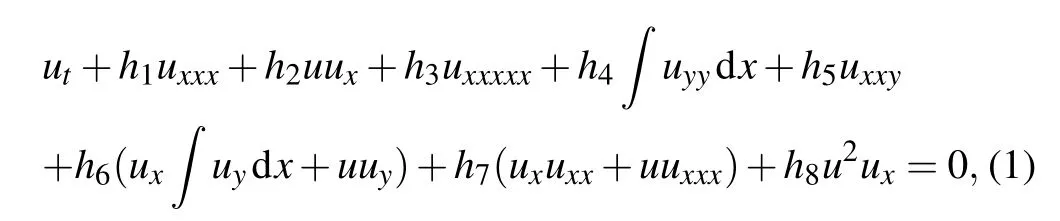
where u=u(x,y,t) and hi(i=1,2,...,8) are real constants.This equation has been widely used in ocean dynamics, fluid mechanics, and plasma physics.[39–41]It is noted that under some special cases, the equation (1) corresponds to different physical models. For example, when h1=h2=0, h3=1,h4=h5=?5, h6=?15, h7=15, and h8=45, the equation turns to the (2+1)-dimensional B-type KP equation for the shallow water wave in fluids or electrostatic wave potential in plasmas.[42–45]While when h2=6h1, h6=4h5, and h3=h4=h7=h8=0, the equation becomes to the (2+1)-dimensional breaking soliton equation for the interactions between a long wave propagating along the x axis and a Riemann wave along the y axis.[46,47]Therefore, it would be of great interest to study the general (2+1)-dimensional KDKK equation(1).
To conclude,motivated by the significance of the (2+1)-dimensional KDKK equation and wide applications of the lump and breather solutions,here we would like to investigate the general high-order lumps, breathers as well as their interactions. We hope that the results obtained can help experts to understand and study the propagations of nonlinear localized waves as well as other physical phenomena related. The outline of the paper is arranged as follows. In Section 2,by introducing a special transformation and coefficient constraint,the N-soliton solutions of the (2+1)-dimensional KDKK equation(1) are constructed. In Section 3, by using a long wave limit to the 2M-solitons, the general M-lump solutions are derived and their dynamical behaviors are analyzed. In Section 4, by restricting the conjugate conditions to the parameters, the Tbreather solutions are constructed. Numerical simulations are implemented,which show that the types of breathers and their propagation properties are determined by the parameters selected. In Section 5,some interaction solutions are given. Finally,a short conclusion is attached in the last section.
2. N-soliton solutions to the KDKK equation
In this section, our concern is with the construction of N-soliton solutions to the (2+1)-dimensional KDKK equation (1). For this purpose, a special transformation is introduced via

It is seen that under the coefficient constraints
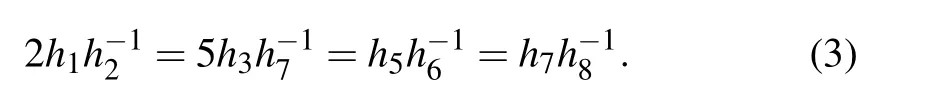
Equation (1) can be readily written into the Hirota bilinear form

where Dx,Dy,and Dtare the bilinear derivative operators defined by
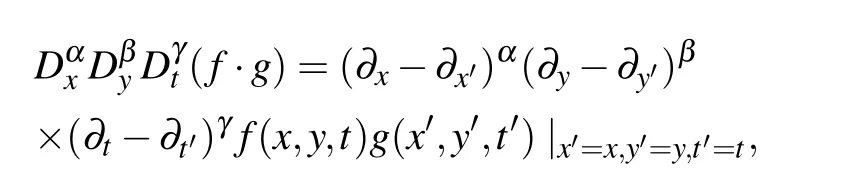
with α,β,and γ being nonnegative integers.
According to the Hirota bilinear direct method,[3]the N-soliton solutions to the (2+1)-dimensional KDKK equation(1)are derived

where
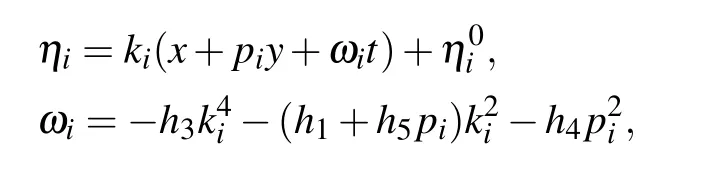
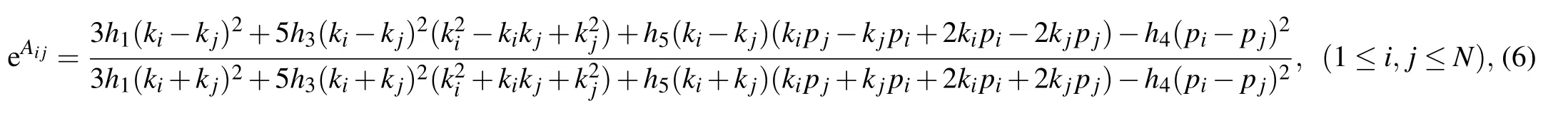
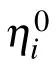
3. M-lump solutions to the KDKK equation
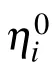
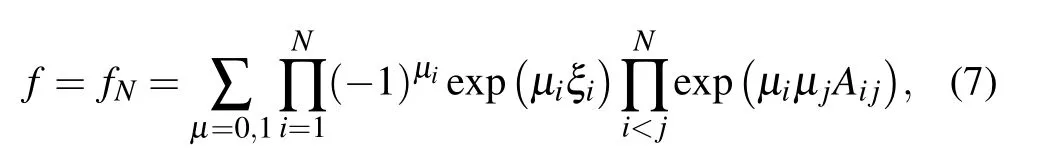
with
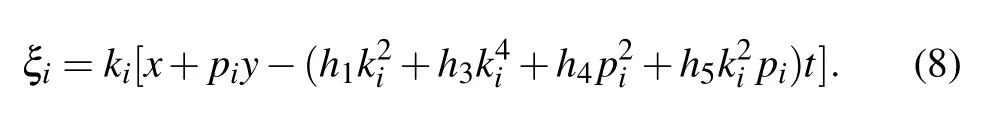
On taking a limit when ki→0,we get
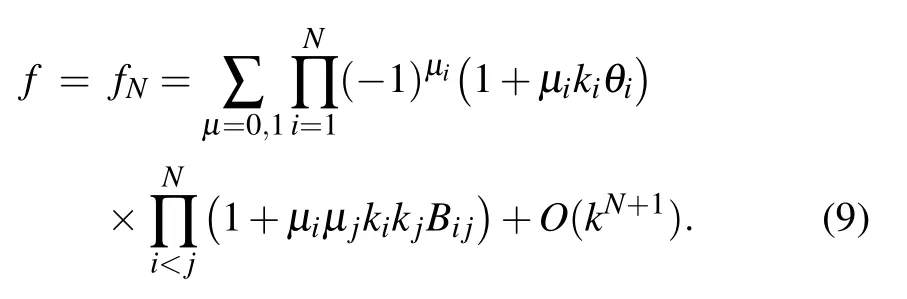

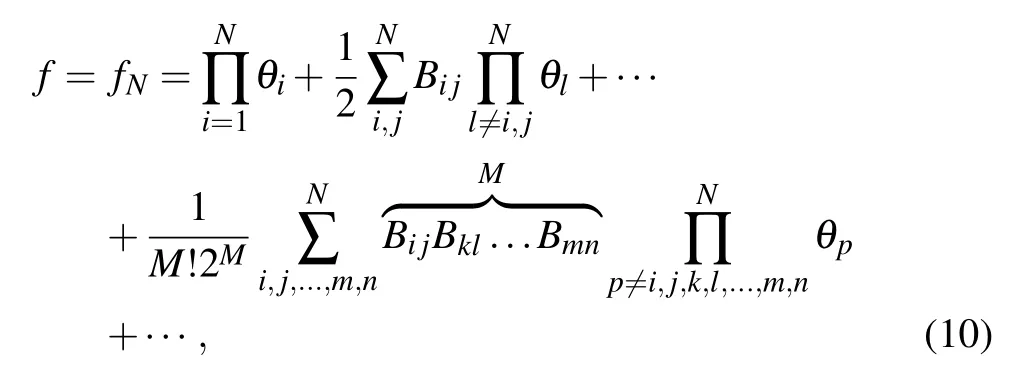
where
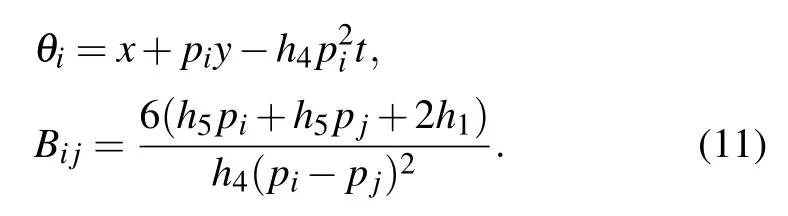

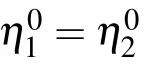
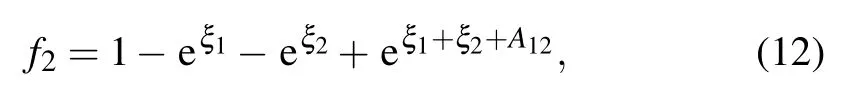
where
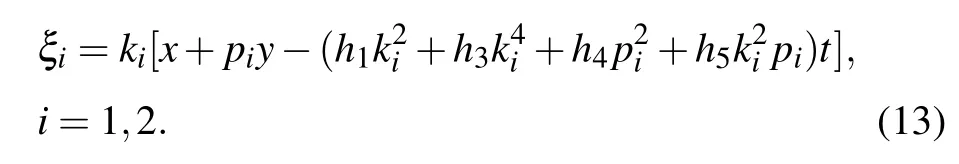
When we apply the long wave limit of ki→0 to f2and omit the constant factor k1k2,we can get

where θ1,θ2,and Bijare defined by
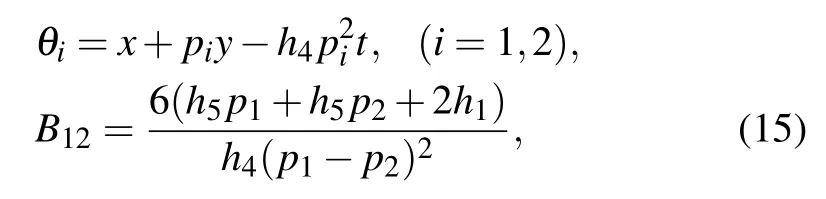
with pibeing complex constants. In order to obtain the lump solution,we set p2=p?1=a?ib in Eq.(15),so the expression of f2is reducible to
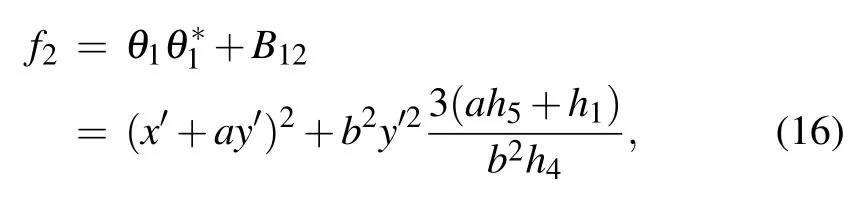
where
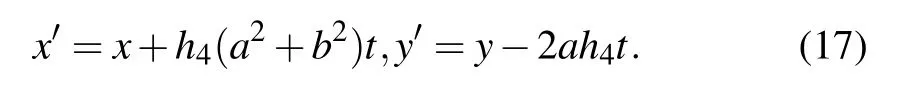
When requiring the relation

and substituting Eq.(16)into the following expression:
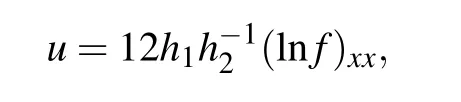
we obtain the 1-lump solution

The lump solution keeps moving along the line

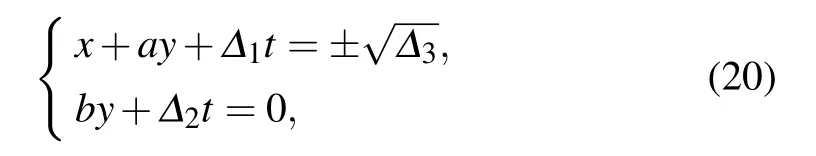
with
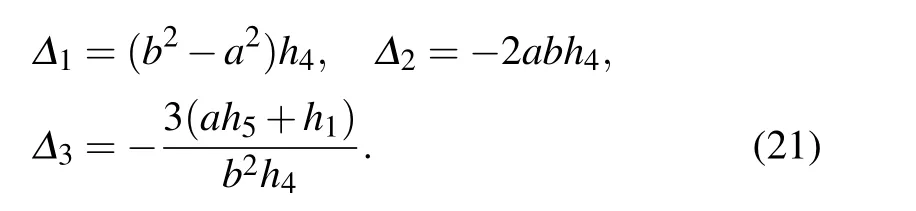
It can be checked that the solution (18) is a constant and keeps moving in a permanent lump status at the velocity of vx=?h4(a2+b2)and vy=2ah4.The 1-lump solution reaches its maximum

However,when(x,y)→∞,the solution decays. Here we take the parameters a=b=1 to exhibit the dynamical behaviors the 1-lump solution may posses. It can be seen from Fig.1 that the 1-lump solution shows bright and dark solitons’ behaviors. Moreover, such a solution keeps its velocity, shape,and amplitude unchanged during propagations.
f4 = θ1θ2θ3θ4+B12θ3θ4+B13θ2θ4+B14θ2θ3
+B23θ1θ4+B24θ1θ3+B34θ1θ2+B12B34

where
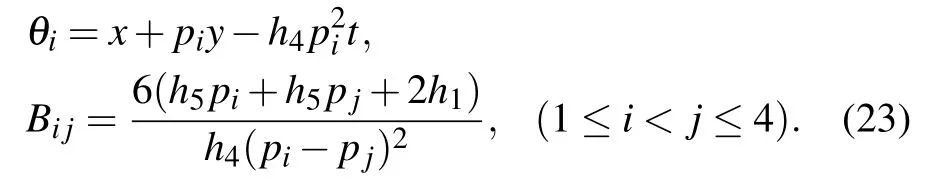
When taking
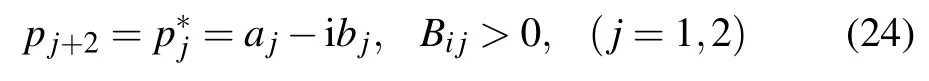
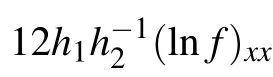
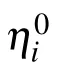
In the above discussion, we have shown that when N =2M and taking the long wave limit to the 2M-solitons,the general M-lump solutions will be generated. Such lump solutions are nonsingular and rationally localized. In the following,we shall demonstrate that when only adopting certain conjugation constrains to the parameters involved in 2T-solitons,the general T-breather solutions will be constructed.
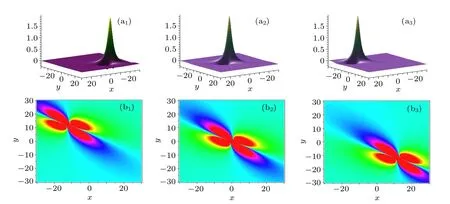
Fig.1. Time evolutions of the 1-lump solution on xoy plane. The time is chosen as t=3(i?2)for(ai)and(bi).
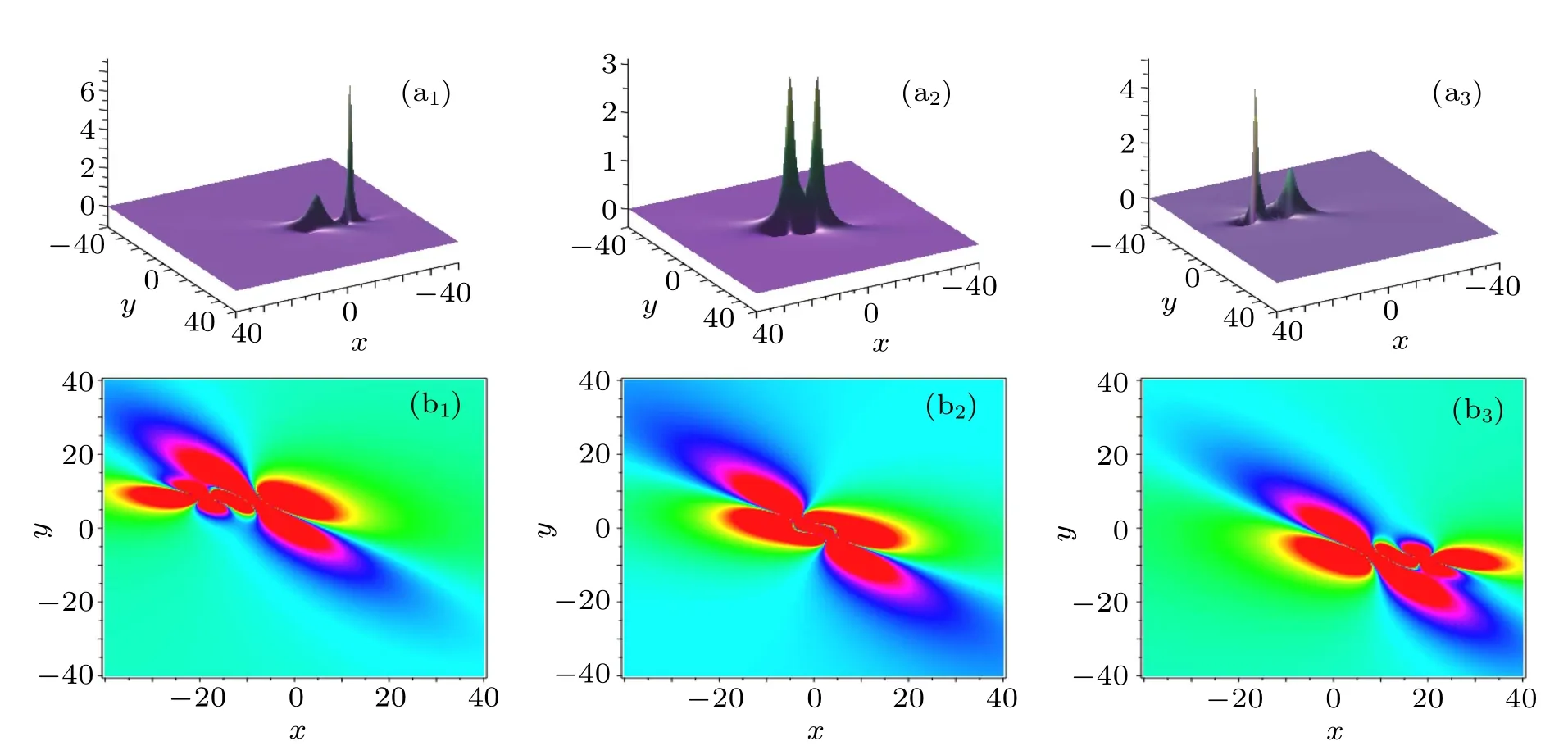
Fig.2. Time evolutions of the 2-lump solution on xoy plane. The time is chosen as t=2i?4 for(ai)and(bi).
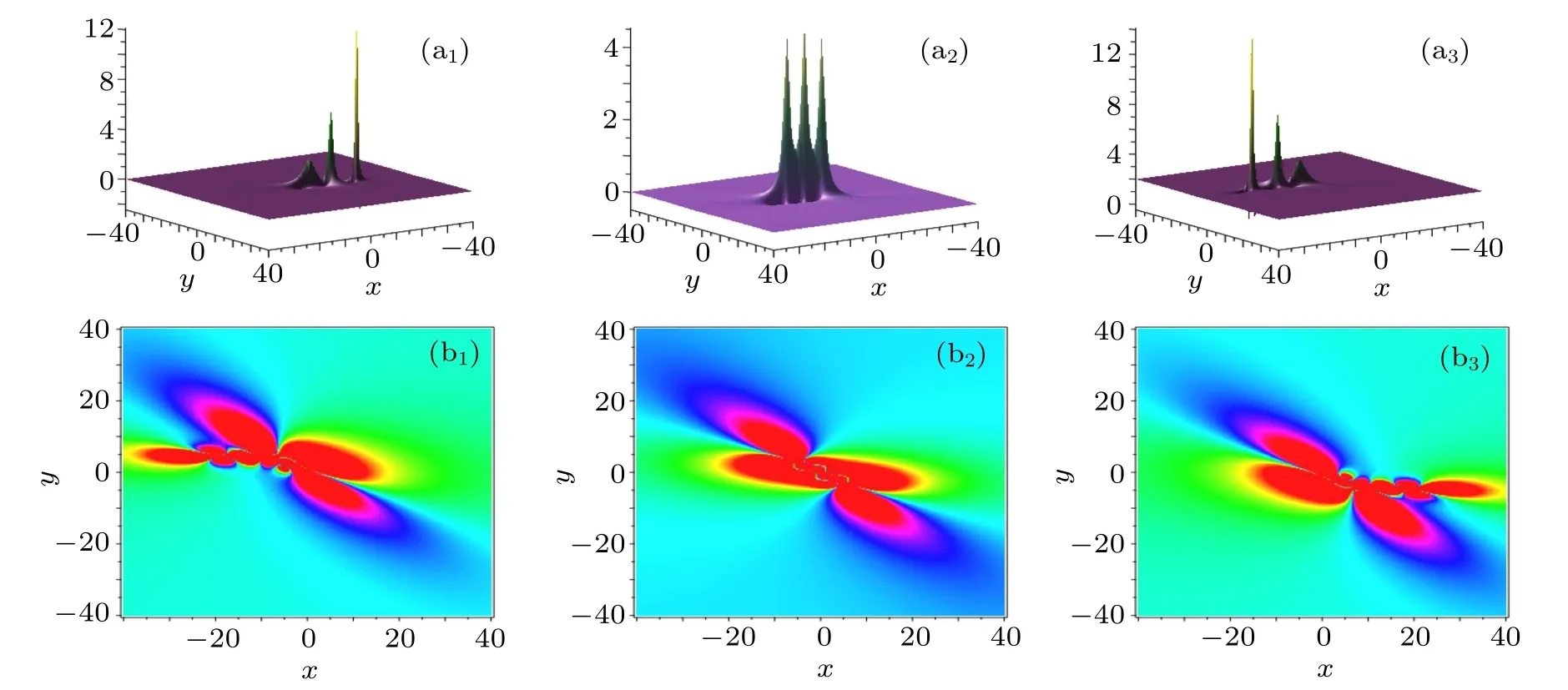
Fig.3. Time evolutions of the 3-lump solution on xoy plane. The time is chosen as t=i?2 for(ai)and(bi).
4. T-breather solutions to the KDKK equation
In this section, we plan to construct high-order breather solutions to the KDKK equation. Hence, we introduce the conjugate constraints:

to the parameters involved in the 2T-soliton solutions(5)and(6). For example,when N=2,one can take the complex conjugate conditions as
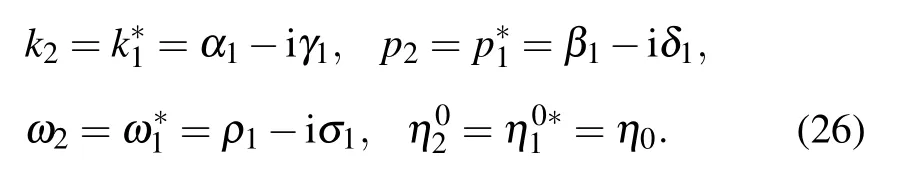
On inserting the above relation into Eq.(5),we can obtain the first-order breather solution,which is expressed by

with
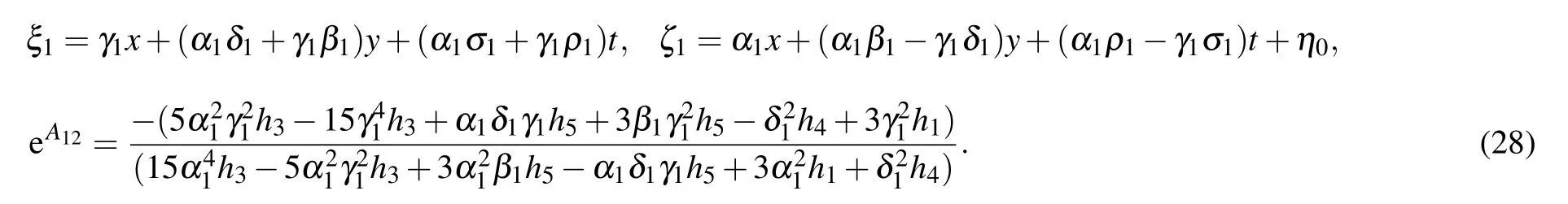

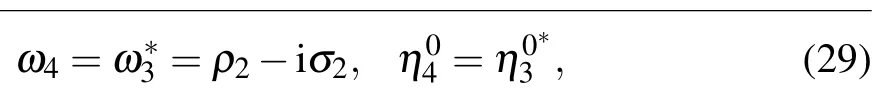
we can obtain the second-order breather solutions. The propagations features and dynamical behaviors of these 2-breather solutions are detected in Fig.5. It can be seen from these figures that the 2-breather solutions consist of two first-order breathers. Like the 1-breather solution, they also exhibit three types of dynamical behaviors due to the parameters{ki,pi} (i=1,2,3,4) selected. For example, when kiare all pure imaginary numbers and piare complex numbers, the 2-breather solutions are shown to be periodic along the x axis,see Figs.5(a1)and 5(b1). When kiare complex numbers and piare pure imaginary numbers, the 2-breather solutions turn to be periodic along the directions which are perpendicular to each other, see Figs. 5(a2) and 5(b2). While when k1is real number, p1is pure imaginary number and k3, p3are complex numbers, the 2-breathers are shown be periodic along the directions intersecting each other at a certain angle, see Figs.5(a3)and(b3).
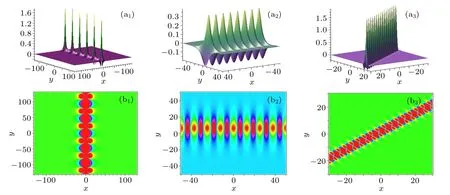
Fig.4. Three types of behaviors of the first-order breather solution in xoy plane. The parameters are chosen as follows. In panels(a1)and(b1):k1=1/5, p1=(2/3)i;in panels(a2)and(b2): k1=(1/2)i, p1=(1/3)i;in panels(a3)and(b3): k1=1/2+i,p1=1/2+i.

Fig.5. Three types of behaviors of the 2-breather solution in xoy plane. The parameters are chosen as follows. In panels(a1)and(b1): k1=i,k3=(1/2)i, p1=1+i, p3=?1+(1/2)i;in panels(a2)and(b2):k1=(1/3)+i,k3=?1+(1/2)i, p1=(2/3)i, p3=?(1/2)i;in panels(a3)and(b3): k1=1/4,k3=(1/2)+i, p1=(2/3)i, p3=(1/2)+i.
5. Hybrid wave solutions of the KDKK equation
5.1. Two kinds of hybrid solutions for N=3
When N=3,from Eq.(5),one can easily write down the expression of f3,which is
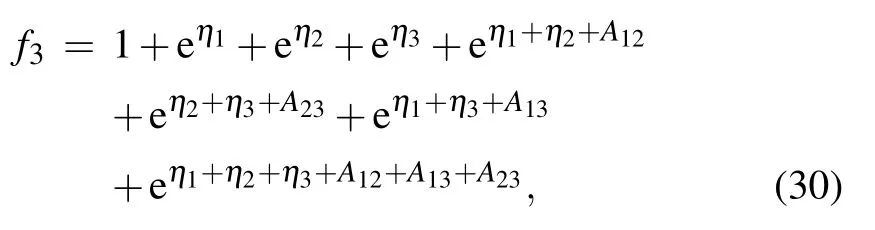
where ηi, Aij(i,j=1,2,3) are described in Eq. (6). In this subsection, two different techniques are applied to Eq. (30)and thereby two kinds of hybrid solutions are constructed.One is a kind of solution mixed by one lump and a stripe soliton via the long wave limit method established in Case 1. The other is a kind of solution combined by one breather and a strip soliton via the conjugate constraint method established in Case 2.
Case 1An interaction solution between one lump and a stripe soliton
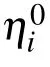
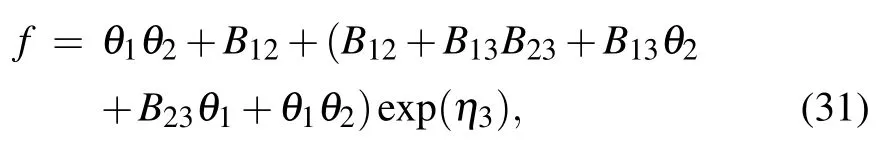
where
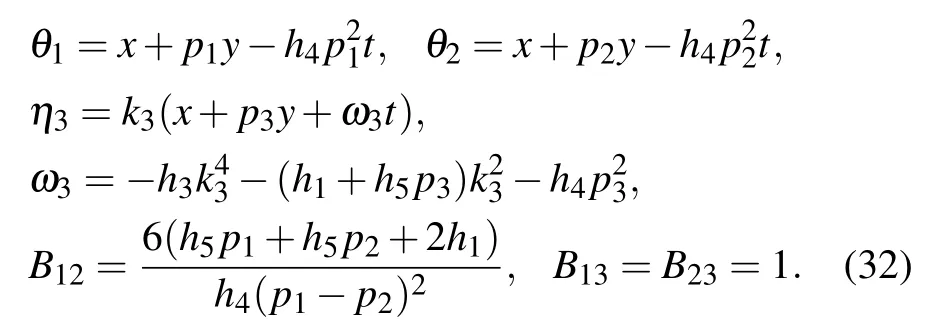
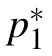

Fig.6. Interaction behaviors of the hybrid solution given in Eq.(31). The time is chosen as t=3i?6 in panels(ai)and(bi).
Fig.7. Interaction behaviors of the hybrid solution given in Eq.(34). The parameters are chosen as p1=(5/4)i,k1=1/4,k3=2,and p3=2.The time is chosen as t=3i?6 for the figure(ai)and(bi).
Case 2An interaction solution between one breather and a stripe soliton
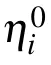
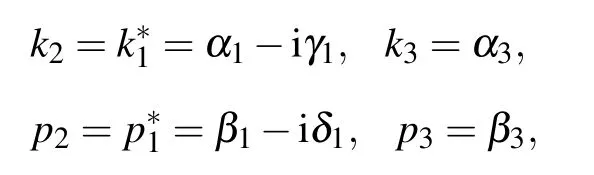

Substituting them into f3in Eq.(30),then we obtain
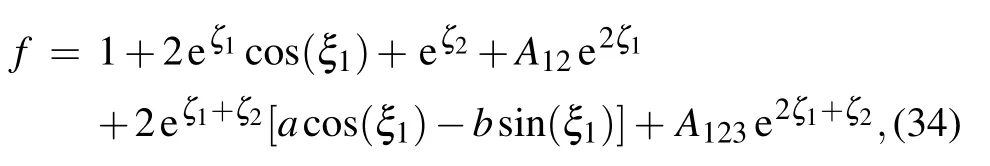
where
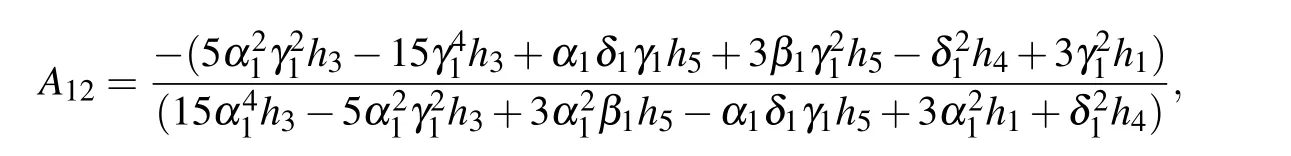

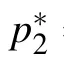
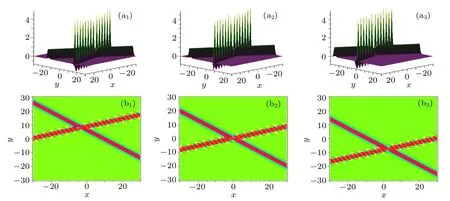
Fig.8. Interaction behaviors of the hybrid solution given in Eq.(34). The parameters are chosen as p1=1/2+2i,k1=1/2+i, p3=1.5,and k3=1.2. The time is chosen as t=3i?6 for the figure(ai)and(bi).
5.2. Three kinds of hybrid solutions for N=4
When N =4, from Eq. (5), one can get the expression of f4. By taking long wave limit and restricting the conjugate conditions to f4,three kinds of hybrid wave solutions can be obtained. Details are as follows.
Case 1 Two hybrid solutions between one lump and one breather or two bell-shaped solitons
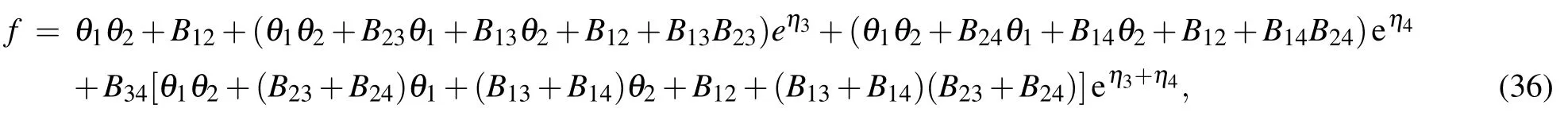
where


Fig.9. Interactions of the hybrid solution between one lump and one breather. The parameters are chosen as p1 ==1+i,k3 ==(7/10)i,and p3==2i. The time is chosen as t=3i?6 for(ai)and(bi).

Fig.10. Interactions of the hybrid solution between one lump and one breather. The parameters are chosen as p1==1+(3/2)i,k3==1/3,and p3==(11/10)i. The time is chosen as t=3i?6 for(ai)and(bi).
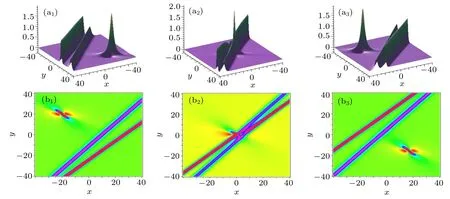
Fig.11. Interactions of the hybrid solution between one lump and two bell-shaped solitons. The parameters are chosen as p1 = =1+i,k3=1.2, p3=?1.1,k4=0.8, p4=?0.9. The time is chosen as t=5i?10 for(ai)and(bi).
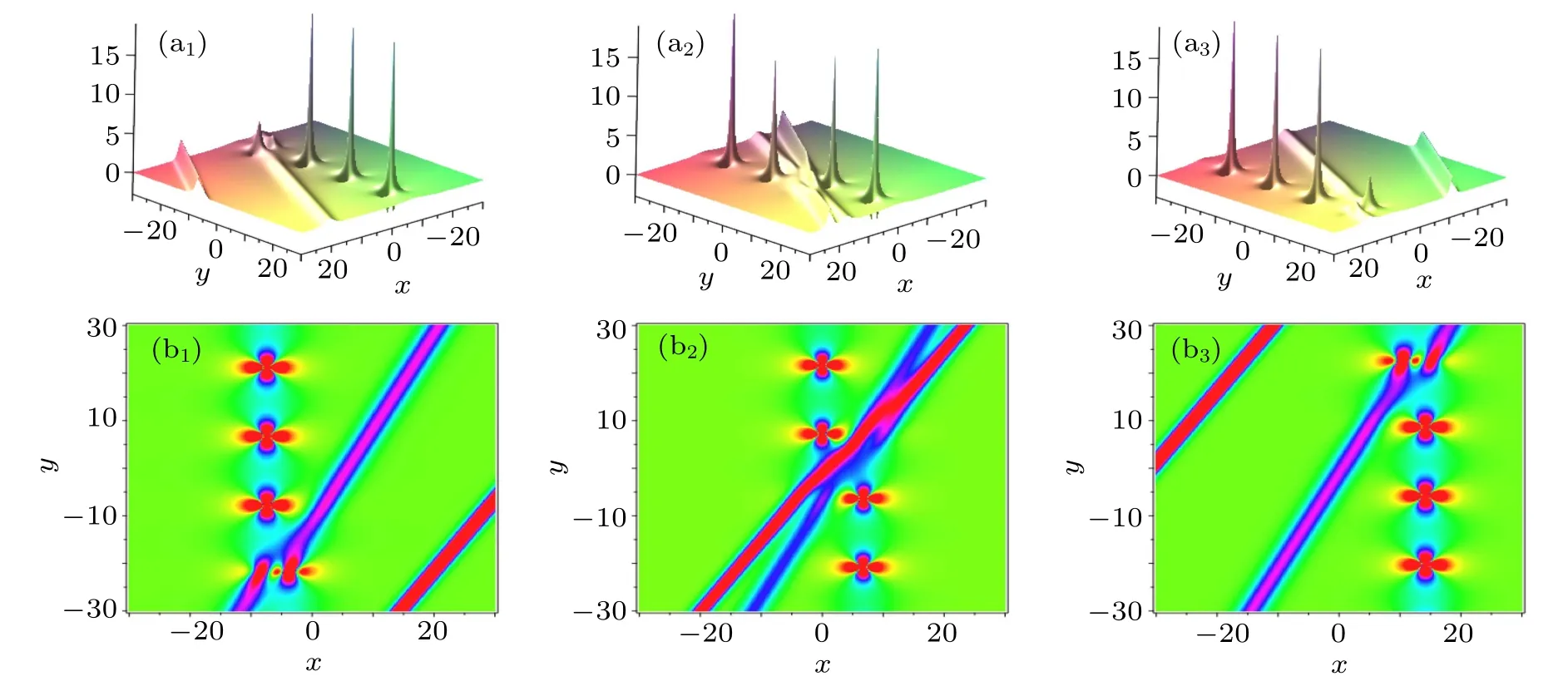
Fig.12. Interaction behaviors between the breather and two bell-shaped solitons. The parameters are chosen by p1==(13/12)i,k1==2/5, p3=?0.5, p4=?2/3,k3=1,and k4=1.8. The time is chosen as t=3i?6 for(ai)and(bi).
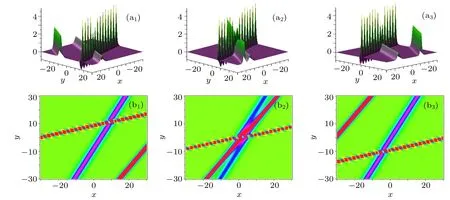
Fig.13. Interaction behaviors between the breather and two bell-shaped solitons. The parameters are chosen by p1==(1/2)+i,k1==(1/2)+i, p3=?0.5, p4=?2/3,k3=1,and k4=1.8. The time is chosen as t=3i?6 for(ai)and(bi).
(ii) When p2=and p3, p4, k3, and k4are real num-Substituting them into the expression of f4given by Eq. (5),we obtain an interaction solution between one breather and two bell-shaped solitons. When we take the parameters as p1==(13/12)i, k1==2/5, p3=?0.5, p4=?2/3,k3= 1, and k4= 1.8, and the breather in the hybrid solution is shown to be periodic along the y axis, seen in Fig.12.While when we take p1==1/2+i, k1==(1/2)+i,p3=?0.5, p4=?2/3, k3=1, and k4=1.8, the breather in the hybrid solution is shown to be periodic along the directions intersecting to xoy plane,seen in Fig.13.

6. Conclusion
The investigation on exact solutions of the nonlinear equations is important and necessary because such solutions can better help us to understand the physical phenomena described by the model and lead to further applications. In this paper, we use the special transformation (2) to construct Nsoliton solutions of the(2+1)-dimensional generalized KDKK equation. By taking the long wave limit and the complex conjugation conditions to the N-solitons,we obtain the general-lumps, T-breathers, and localized interaction solutions. Numerical simulations show that for the-lumps, they usually collide with each other at certain time and their interactions are nonelastic (see Figs. 2 and 3). For the T-breathers and hybrid solutions, they have much richer dynamical behaviors than lumps, (see Figs. 4–13). Such behaviors are affected by the parameters selected. However, for the more complicated interaction solutions, due to the complexity in selecting the parameters,it is rather difficult to study their interactions,but they are worthy of deep investigation. In addition,how to use the solutions obtained to explain some physical phenomena,for example catastrophic weather and huge waves,is deserved our considerations. Meanwhile,whether the KDKK equation admits the multiple wave solutions is also an interesting questions deserved investigation. Based on the significance of the localized wave solutions and wide application of the KDKK equation, all these questions mentioned above will be further studied in the near future.
- Chinese Physics B的其它文章
- Quantum annealing for semi-supervised learning
- Taking tomographic measurements for photonic qubits 88 ns before they are created*
- First principles study of behavior of helium at Fe(110)–graphene interface?
- Instability of single-walled carbon nanotubes conveying Jeffrey fluid?
- Relationship between manifold smoothness and adversarial vulnerability in deep learning with local errors?
- Weak-focused acoustic vortex generated by a focused ring array of planar transducers and its application in large-scale rotational object manipulation?

