OLD AND RECENT RESULTS IN THE ANALYTIC THEORY OF DIRICHLET SERIES: A SURVEY*

Herv′e QUEFF′ELEC

Universit′e des Sciienes et Technologies de Lille, Laboratoire Paul Painlev′e U.M.R. CNRS 8524,U.F.R. de Math′ematiques, 59 655 VILLENEUVE D’ASCQ Cedex, FRANCE E-mail: herve.queffelec@univ-lille.fr

Abstract This survey is dedicated to the memory of Professor Jiarong Yu, who recently passed away. It is concerned by a topic of which he was fond, an interest shared by myself:the analytic theory of Dirichlet series.

Key words Dirichlet series; analytic theory

1 Memories

I met Professor Jiarong Yu in the University of Orsay(now Paris-Saclay)in the mid-eighties,when he was visiting this University at the invitation of my former supervisor J. P. Kahane,for a long stay (two months or so). I knew (and J. P. Kahane had recommended him to me)that he was an expert in the analytic theory of Dirichlet series in the style of H. Bohr and S. Mandelbrojt: this topic had been that of his “Th`ese d’′Etat” supervised by G. Valiron, and had also been part of my Habilitation; hence I was curious to meet him and discuss with him on this question. Our encounter took place in Kahane’s office. I remember this first contact:I found a very friendly, simple, and smiling man, who looked pretty young to me (Chinese privilege to keep black hair nearly indefinitely···), even if he was fairly older than I. Later on, I met him again several times during his stay, we realized during our discussions that our interests and domains of expertise were rather close to each other, and considered the idea to begin a joint work on those Dirichlet series. Finally, this did not happen, mainly by lack of time of both of us, and today I regret it a little.

Later on (1994), Mr Jiarong Yu founded the Chinese-French center of Mathematics in Wuhan, and sent many of his brilliant students abroad,notably in France(Paris,Lille,Amiens,Besan?con, etc···) where I was able to meet some of them. Twenty years after our encounter in Orsay, when I happened to visit Wuhan, or Beijing, I tried to meet him again. But his health was already rather poor at that time, and it turned out not to be possible. I will keep the memory of a very human, modest and kind person, independently of his mathematical talent.And it is good that Mathematics unite people!

The survey to follow is not designed for experts, but for the widest possible audience of analysts. It has no claim to exhaustivity. In preliminary sections, we give some reminders and definitions. Then, more specifically, we consider:

A The optimality in a famous product theorem of Landau.

B The optimality of the shift 1/2 between the abscissas of uniform and absolute convergence of a Dirichlet series.

C The rate of growth of the analytic extension of a Dirichlet series beyond its half-plane of convergence. This extension can have surprisingly severe growth.

D A tentative update of some aspects of the theory.

In cases A and B,the examples are not as explicit as that which follows Theorem 2.2(as far as we know, no really explicit example is known for either of Theorems 4.2 and 5.1). They will instead be based on the use of Baire’s lemma, a “profound triviality” to quote T. K¨orner (Kahane loved this formulation!); this lemma is in particular the key to the fundamental theorems of Functional Analysis, as the Banach-Steinhaus theorem to be used here.

2 Abscissas Attached to a Dirichlet Series

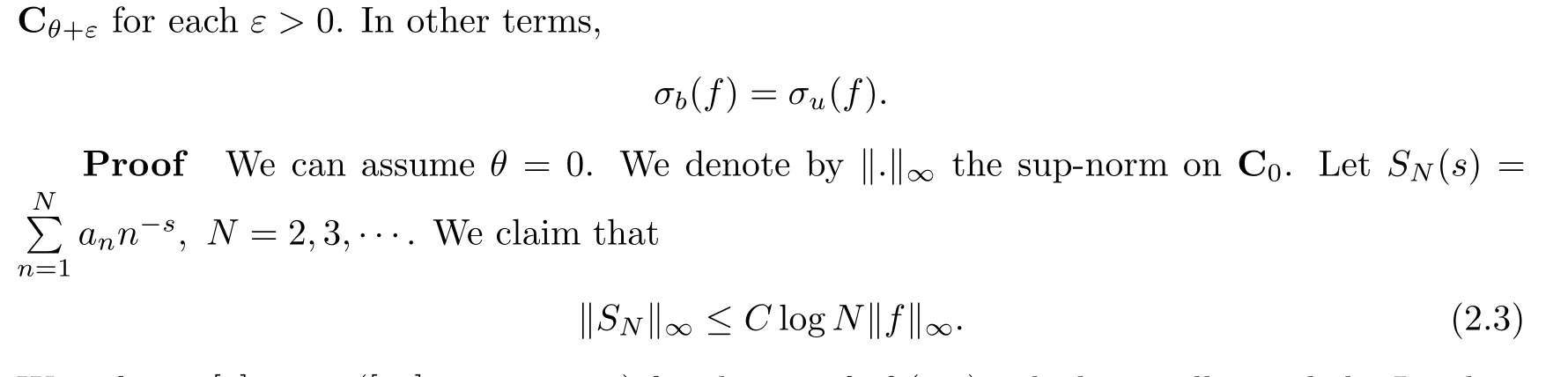
We refer to [3] or to ([30], p. 149-151) for the proof of (2.3), which initially used the Landau-Perron formula. An alternative real variable proof is due to E. Saksman(see, e.g. ([7], p. 561),the proof is given for H1but works word for word for H∞). Once you have (2.3), the result follows by Abel summation.□

We return to this partial sums issue in the final section.

In strong contrast with the case of Taylor series, for which the circle of convergence always contains a singular point, it may very well happen that, given a Dirichlet series, one has for example σc= 0 and σh= -∞. Once you know the basics on the Riemann zeta function, you can take the series

Cahen and later Bohr proved the following (in the case of Dirichlet series diverging at the point 0):

Bohr’s theorem implies that σc(X) = 0 when X = H∞is the space of those f ∈D which are analytic and bounded in C0. What if the functions of X are nearly bounded in C0? In answer to a question of Hedenmalm, it is shown in the recent paper [2] that, if X is the Hardy-Orlicz space Hψαwith ψα(x)=exp(xα)-1, then

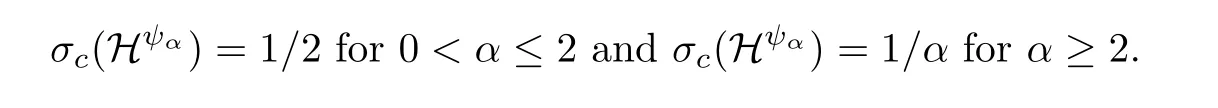
Now,to enunciate and prove our results,we first make a detour through some indicator functions attached to the sum of a Dirichlet series.

3 Lindel¨of and Bohr

3.1 The Lindel¨of functions

Let f be holomorphic in a half-plane Cθ. We coin in this short section two indicator functions (the first one is classical, and the second one a variant which will be useful later)which measure the growth of f inside Cθ:

· The Lindel¨of function μ:(θ,∞)→R+∪{∞} defined as

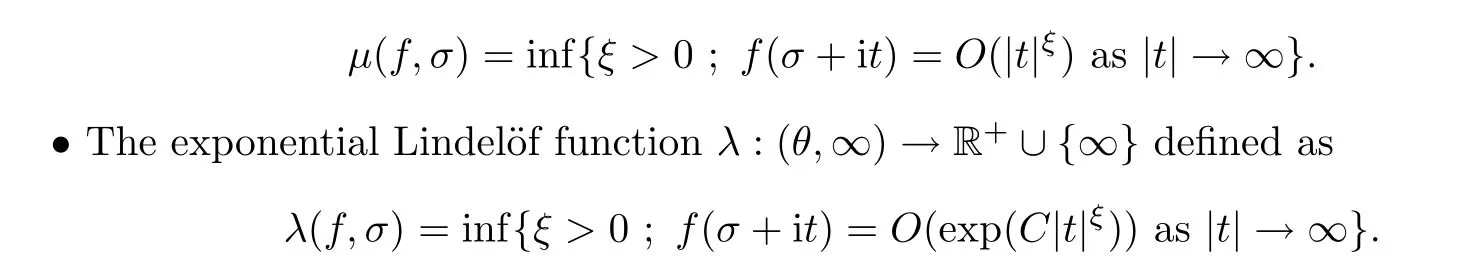
Here, C is some positive constant. We refer to ([28], Lemma 2, p. 552) for the theorem below,in the case of the exponential Lindel¨of function.

3.2 The Bohr lift

This preservation ([30] p. 47-50) is an easy consequence of the Z-linear independence of the real numbers log pkand the Kronecker simultaneous approximation theorem. After those preliminaries, we can come to the results we wish to present.

4 The Product Theorem

The following is elementary ([15] page 67).

Theorem 4.1 (Stieltjes) Assume that f and g above converge at 0. Then, h converges at 1/2+iτ for any real number τ.

Refuting a conjecture of Cahen,Landau([23])proved that this result is optimal as concerns the shift 1/2. H.Bohr found an elegant proof making use of the Lindel¨of function μ just defined.We pursued along that line in [20], with several Dirichlet series, in the style of Landau ([23]).We shall also give a proof based on the Banach-Steinhaus theorem. Here is a precise statement.

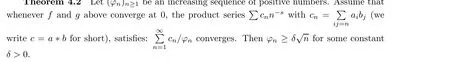
Proof We first indicate the proof of Bohr concerning the optimality of the Stieltjes result.Consider Bohr’s Dirichlet series (3.1) and suppose that the squared series f2converges for σ ＞σ0. Then we simply write, for such a σ:

so that 2(1-σ0)≤1 and σ0≥1/2.

This proof, in our opinion, cannot be qualified of “explicit”. Neither is the proof to come,but it will provide a more precise result. Moreover,this second proof seems to us simpler than Bohr’s construction of a Dirichlet series whose sum satisfies (3.1). Let E be the Banach space of convergent series a=(an)n≥1, equipped with the norm

5 The Abscissa Gap Theorem

6 Wild Growth in Strips

The real issue is the lower bound. We first make the quasi-sure properties more explicit thanks to a simple lemma ([20], Lemma 2.2 page 491).

Playing with σ0and ε, and using that(Baire’s lemma)a countable intersection of q.s. “events”is again q.s., we get that

Theorem 6.1 (via Theorem 3.1) easily ensues by convexity (see also [28], Th′eor`eme 3 p. 554).□

7 A Few Updates in the Theory

7.1 Beurling’s problem

we have that F and 1/F belong to H∞. At this occasion, the authors also revive the tricky device of H. Bohr, the “Bohr lift”, already alluded to several times in this paper. This leads to analysis in infinite-dimension, in particular on the infinite torus T∞, a compact abelian group equipped with its Haar measure, and this viewpoint revealed once more very fruitful. In particular, this paper strongly stimulated work related to operator theory on Banach spaces of analytic functions, as we are going to see.

7.2 Composition operators

Shortly afterwards, the analytic self-maps φ : C1/2→C1/2such that the “composition operator”Cφ:ff ?φ maps H2to itself were characterized in [14], as follows. The self-map φ:C1/2→C1/2must exactly be of the form

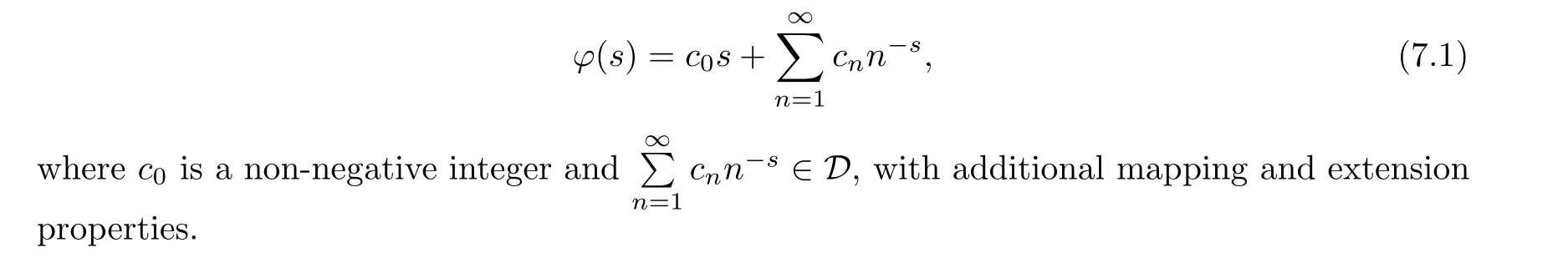
This work was continued in [4] and [5] where new Hardy spaces Hpof Dirichlet series were coined for p /= 2, and the study of the compactness of Cφinitiated. Other papers studied membership of Cφin Schatten classes,more precisely the decay rate of the singular numbers of Cφ. For that aspect, we refer to the paper [31] which emphasizes the great difference between the cases c0= 0 (decay rate not so far from those of self-maps of the disk) and c0≥1 (a brutal change of scale in the decay rate occurs). See also [29, 30] and the references therein, in particular the existence of composition operators Cφ(in the case c0= 0) which are bounded on H2but not on Hpfor 1 ≤p ＜2, thanks to a difficult and recent result of A. Harper; a result which solves in the negative the so-called“l(fā)ocal embedding conjecture”. This conjecture enunciates as follows.

for all f ∈Hp. It is known that (7.2) is true for p=2 (see [30] p. 18-20)and as a consequence for p an even integer. Harper proved that it is wrong for p ＜2, and the remaining cases are open. For the connection with composition operators, see ([6], Thm. 3). We also mention the beautiful book [13], in which the infinite-dimensional aspect, and Banach space-valued holomorphic functions, are studied in depth. Finally, the compactness of Cφwas recently fully characterized(when φ(∞)/=∞, or else when c0=0) in [12].

7.3 Helson matrices

A famous theorem of Nehari([26])gives a characterization of Hankel matrices: those infinite matrices A = (aj,k)j,k∈N0with aj,k= cj+kdepending only on the sum j +k, which define a bounded linear operator on ?2. A necessary and sufficient condition for this boundedness is the existence of some φ ∈L∞(T) such that

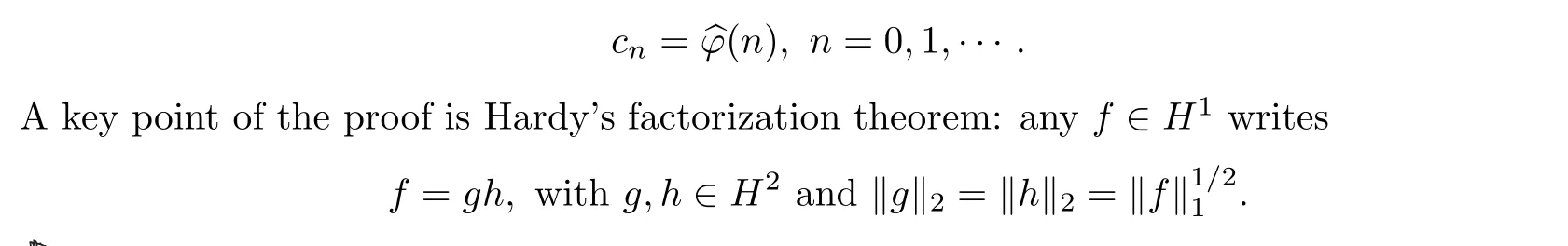
So that in any case the difference of growth between ‖DN‖H1and ‖DN‖H2will be very tiny.This lower bound was improved in various ways([30] p. 176-177),but Helson’s conjecture still resisted. In the mean time, Ortega-Cerd`a and Seip ([27]) solved the Question in the positive,by a simple but ingenious method: there are bounded Helson matrices without symbol,and no Hardy factorization theorem between H1and H2holds. The final word was given by A.Harper([16]) who proved

As a consequence, Helson’s conjecture is true, and one has one more proof of the existence of bounded Helson matrices without symbol.

7.4 Size of partial sums

This example gives a similar lower estimate log log N for the H1-norm, and there is a slight improvement in the H1case ([11], Thm. 5.2), namely

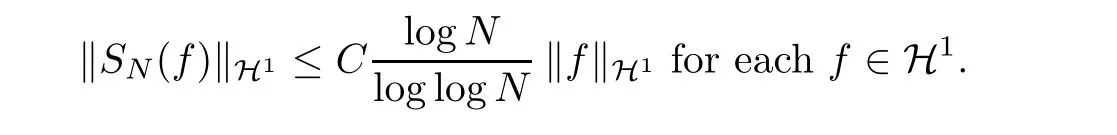
The sequence (n-s)n≥1is a Schauder basis of Hpfor 1 ＜p ＜∞([1]), which amounts to the inequality

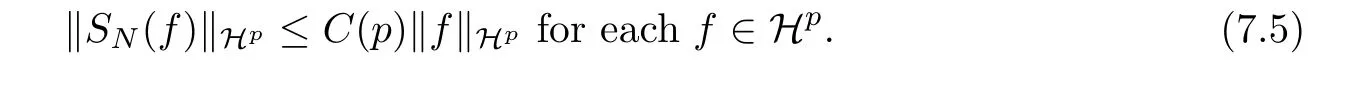
But turning back to p = ∞, what is the real growth of CN? This innocent looking question received no answer since 2006,and it is not even clear what one should expect: log N? log log N?else?

Finally, in the recent work [22], the Riesz projection in infinite-dimension is studied, as well as a space of Dirichlet series with bounded mean oscillation; the size of partial sums

8 A Word of Conclusion

As the interested reader can see, many open and difficult questions remain; and the activity and perspectives in this analytic theory of Dirichlet series would surely have pleased the regretted Professor Jiarong Yu.