QK spaces: A brief and selective survey


For K(t) = t,0 <p <1, the space Dis the usual weighted Dirichlet space D. Clearly,Q=M(D)for 0 <p <1 and BMOA=M(H). In fact,BMOA=M(H)for all 0 <p <∞;see [7, 8].
1.2 Basic properties
Note that D ?Q?B holds for all non-trivial increasing functions K. In particularly,Q=D if and only if K(0)>0; Q=B if and only if

In many situations, the subspace Qis simply the closure of the set of polynomials in Q.Examples include BMOA and the Bloch space. If K = 1, then Qis the Dirichlet space; in this case, the polynomials are dense, but Qconsists of just the constant functions.
Problem 1.1 Find a sufficient and necessary condition on K such that Q=BMOA.
Under the assumption that the weighted function K is concave, a sufficient and necessary condition on K such that Q=BMOA is given in [10].
2 Structure of the Weight Function K
2.1 Weight functions
The function theory of Qspaces obviously depends on the properties of K. To summarize,we make the following standing assumptions on the weight function K from this point onwards,unless otherwise noted:
(a) K :[0,∞)→[0,∞) is non-decreasing and right continuous;
(b) K(0)=0 and K(t)>0 for all t >0.
Note that the space Qdepends only on the behavior of K(t) for t close to 0. Thus, when studying Qspaces, we can always assume that K(t)=K(1) for t ≥1. Consider an auxiliary function
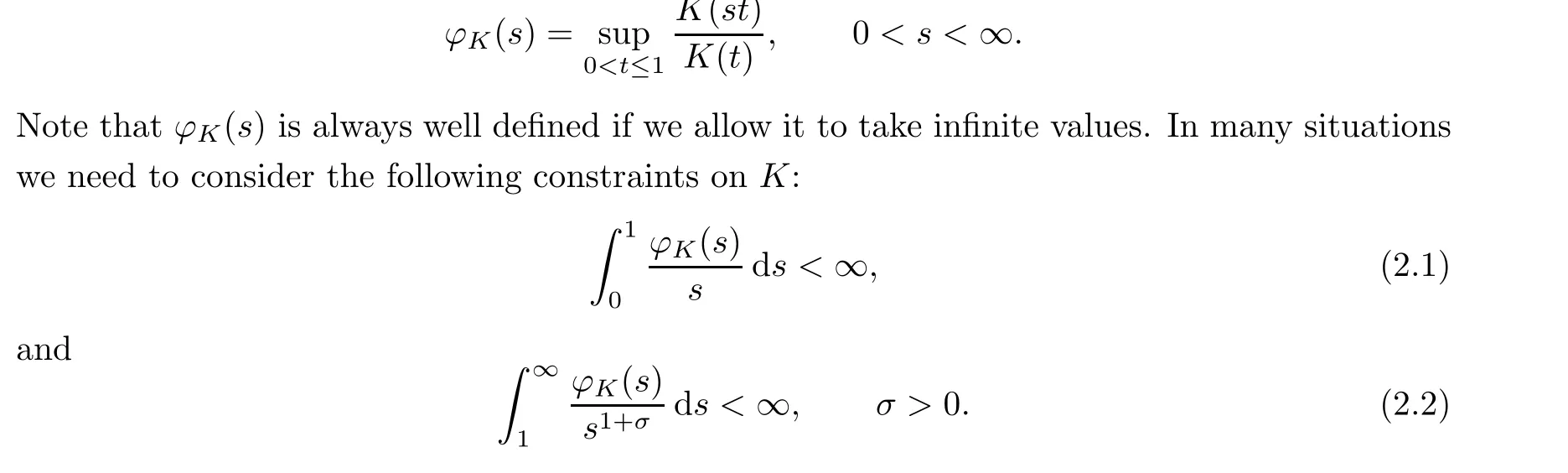
It is clear that the weight function K(t) = tsatisfies (2.1) for 0 <p <∞and it satisfies condition(2.2)whenever 0 <p <σ. We will see that many properties of Qspaces depend on one or two of these conditions.
Suppose that K satisfies (2.1) and the doubling condition on (0,1). Then there exists a weight function K, still satisfying all standing assumptions on weights, such that Kis comparable with K on(0,1)and the function tK(t)is increasing on(0,1)for all sufficiently small constants c >0. Conversely,if the function tK(t)is increasing on(0,1)for some c >0,then K satisfies condition (2.1).
Suppose that K satisfies(2.2)for some σ >0. Then there exists a weight function K,still satisfying all the standing assumptions on weights,such that Kis comparable with K on(0,1)and the functions K(t)/tand K(t)/tare both decreasing on (0,∞) for all sufficiently small constants c >0. Conversely, if the function K(t)/tis decreasing for some c >0, then K satisfies condition (2.2) for all σ>σ-c.
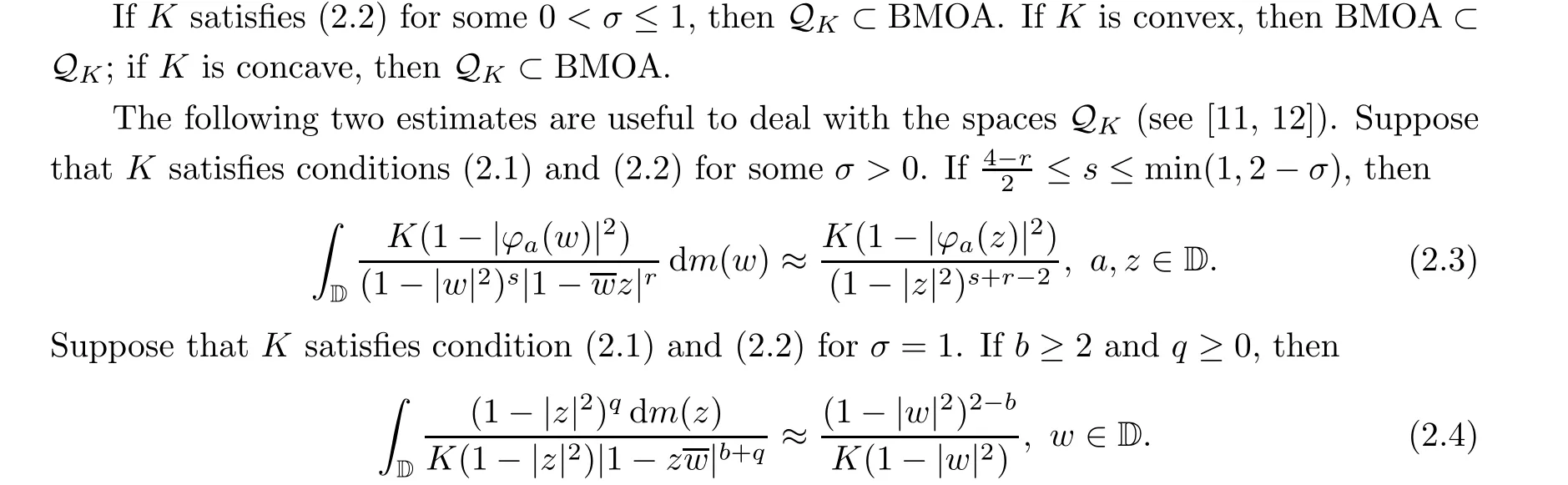
2.2 Weighted Bergman space

3 K-Carleson Measures
3.1 Definitions
A very useful tool in the study of Qspaces is the K-Carleson measure. For an arc I with its length |I|<1, define the Carleson box by

3.2 Fractional order derivatives and Morrey K-spaces

3.3 Decomposition


3.4 Multiplication operators and the space of multipliers
Let X be a Banach space of analytic functions in D. A function g ∈H(D) is said to be a multiplier of X if the multiplication operator

is bounded on X. The space of all multipliers of X is denoted by M(X).
The space of multipliers is known for several classical spaces such as Hardy and Bergman spaces, and in particular for H= D, the space of multipliers M(H) = H, the algebra of bounded analytic functions. For other Dirichlet spaces D,0 <p <1, the situation is more complicated.
It is convenient at this point to consider the space W, introduced by Rochberg and Wu[22], consisting of g ∈H(D) such that the measure

4 Derivative-free Characterizations
4.1 Inner functions in QK spaces
In this and the next subsection, we suppose that K satisfies (2.1) and (2.2) for σ =1. An inner function I is analytic on D, having the properties |I(z)|≤1 for all z ∈D and |I(e)|=1 a.e. on ?D. Of course, any inner function belongs to BMOA. However, this fact is no longer true for Qfor 0 <p <1.
Let X and Y be two spaces of analytic functions in D with X ?Y. An inner function I is said to be (X,Y)-improving if If ∈X whenever f ∈X and If ∈Y. This notion was introduced by Dyakonov [26]. For 0 <p <1, Pel′aez [27] characterized (Q,B)-improving and(Q,BMOA)-improving inner functions. We generalized these results to Qspaces by different techniques (cf. [28]). Later, a simple proof was given in [29].
The following are equivalent for an inner function I (cf. [14, 28, 29]):
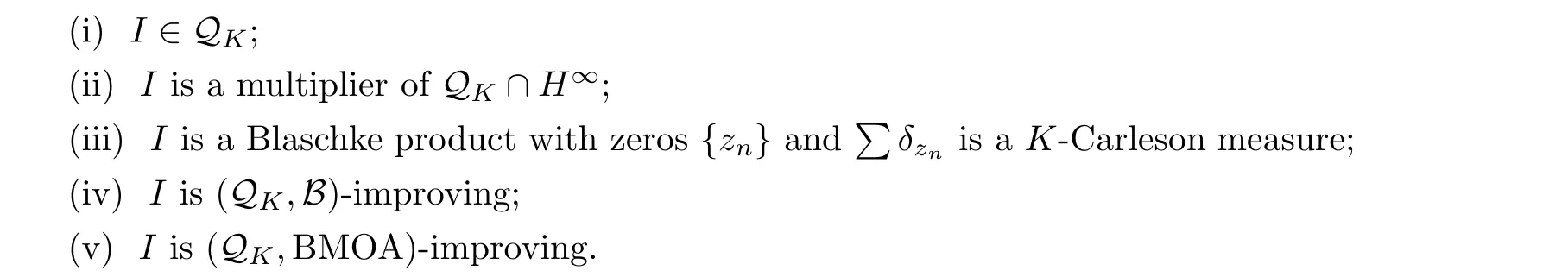
4.2 Inner-Outer decomposition
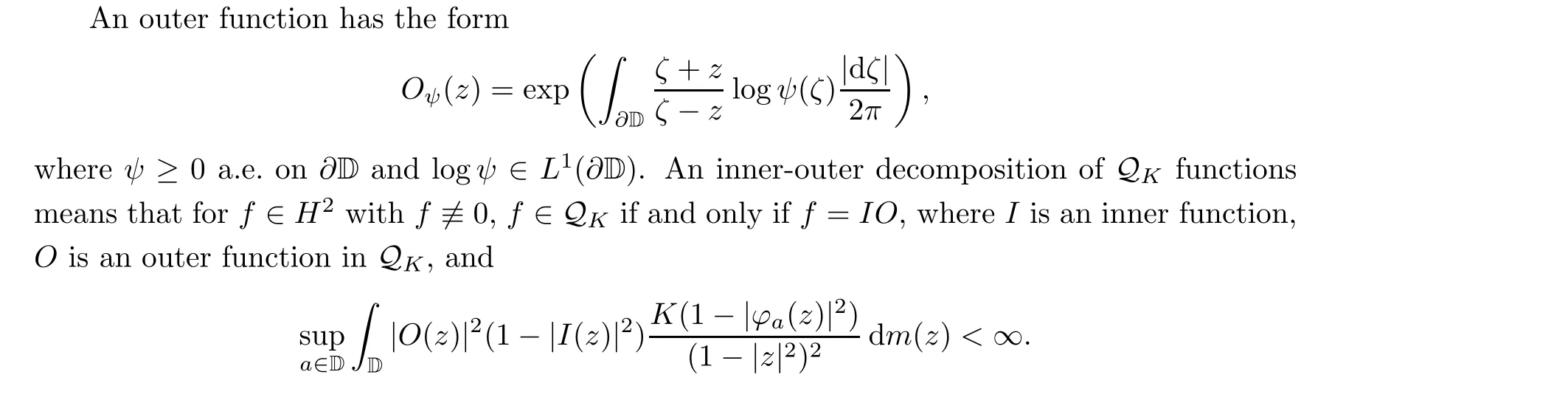
This result can also be used to construct outer functions in Qand to represent a Q-function as the ratio of two bounded functions in Q; that is, if f ∈Q, then there are functions fand fin H∩Qsuch that f =f/f. See [14].
4.3 Derivative-free characterizations
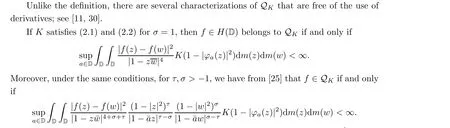

5 Connection Between QK-theory and Others
5.1 Relationship to Teichm¨uller spaces
The universal Teichm¨uller space, denoted by T(1), is defined as the set of all functions g = log fin the unit disk D, where f is conformal in D and has a quasi-conformal extension to the complex plane C. As a bridge between the space of univalent functions and general Teichm¨uller spaces, T(1) is the simplest Teichm¨uller space.
The BMO-Teichm¨uller space,denoted by T,is the subset of T(1)consisting of all functions g =log f∈T(1) such that


is a K-Carleson measure on D, where Sis the Schwarzian derivative of f.
Suppose that K satisfies (2.1)and (2.2)for some 0 <σ <2. Then T?Q. More results on Q-Teichm¨uller spaces can be found in [15, 40].
5.2 Connections to complex differential equations

where α=α(n,σ,K)>0, then all solutions of (5.1) belong to the Qspace.
5.3 Composition operators on QK spaces
Let φ be an analytic self-map of the unit disk D. The equation C(f) = f ?φ defines a composition operator Con the space of holomorphic functions in D. A fundamental problem in the study of composition operators is to determine when Cmaps boundedly or compactly between various Banach spaces in H(D). The study of such operators has attracted a lot of attention (cf. [44, 45]). Related spaces include the Hardy space,the Bergman space, the Bloch space, the Dirichlet space, BMOA and so on. Composition operators played a key role in De Branges’s renowned proof of the Bieberbach conjectures [46, 47]. It should be mentioned that the Carleson measure and its various generalizations are important tools in the study of composition operators (cf. [48, 49]).
It is not difficult to see that every composition operator Cis bounded on BMOA, as a consequence of Littlewood’s inequality. Significant progress on the compactness of composition operators Con BMOA was made by Bourdon, Cima and Matheson [50] and Smith [51]. A more straightforward description for the compactness of Con BMOA was obtained in [52,53]. However, we know almost nothing about the boundedness or compactness of composition operators on Qeven on Qspaces for 0 <p <1, despite efforts by several mathematicians in recent years.
Problem 5.1 Give a function-theoretic characterization of φ such that the composition operator Con Q, 0 <p <1, is bounded or compact.
Problem 5.2 Give a function-theoretic characterization of φ such that the composition operator Con Qis bounded or compact.
6 More Results on QK Spaces
6.1 Duality and Korenblum’s inequality

6.2 Distances from Bloch functions to QK spaces
Suppose that X ?B is an analytic function space. The distance from a Bloch function f to X is defined by
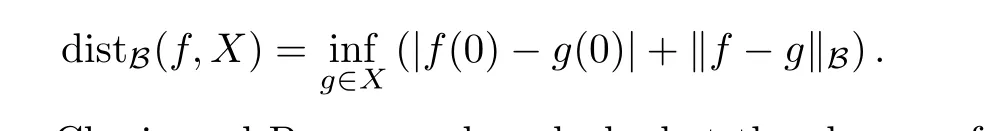
In 1974, Anderson, Clunie and Pommerenke asked what the closure of the bounded functions in the Bloch space is (see [58]). This is still an open problem. The problem of estimating the distance from a Bloch function to various subspaces of the Bloch space has been studied in many papers. After ten years, Anderson in [59] mentioned that Jones gave an unpublished result(Jones’distance formula)that for f ∈B, f is in the closure of BMOA in the Bloch space if and only if

6.3 QK and the range of the ces′aro operator acting on H∞

6.4 Zero sets of QK spaces
A sequence {z} in D is said to be a zero set of X ?H(D) if there is an f ∈X such that f vanishes on {z} and nowhere else. Recall that a Carleson-Newman sequence is a finite union of interpolating sequences for H. Suppose that K satisfies(2.1)and(2.2)for σ =1. Let{z}be a Carleson-Newman sequence in D. In [28] we proved that {z} is a zero set of Qif and only if there exists an outer function g ∈Qsuch that
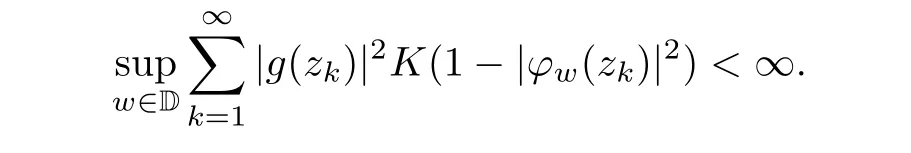
The authors of [70] gave some charactrizations for zero sets of D, and showed that Dand Qhave the same zero sets for 0 <p <1.
Problem 6.1 What are zero sets of Q? Do Qand Dspaces have the same zero sets?
7 QK Spaces on the Unit Circle
7.1 QK(?D) spaces

A result in [14] shows that f ∈Hbelongs to Qif and only if its boundary function belongs to the boundary Qspace. Meanwhile, f ∈L(?D) belongs to Q(?D) if and only if|??f(z)|dm(z) is a K-Carleson measure.
7.2 Fefferman-Stein decomposition
The well-known Fefferman-Stein decomposition theorem [71, 72] states that an arbitrary BMO function can be represented as the sum of an Lfunction and the conjugate of another such function. An analogue of this theorem in the context of Qspaces, due to Nicolau and Xiao [73], can be stated as follows: for p ∈(0,1), f ∈Hbelongs to Qif and only if f can be written as f+if, where f,f∈H(D) and Ref,Ref∈L(?D)∩Q(?D). A similar result (cf. [74]) for the boundary Qspaces can be written: a function f ∈L(?D) belongs to Q(?D) if and only if f =u+~v, where u,v ∈L(?D)∩Q(?D).
7.3 ˉ?-problem

7.4 The corona and Wolfftheorems

8 QK Spaces in the Higher Dimentional Cases
8.1 QK spaces of several real variables

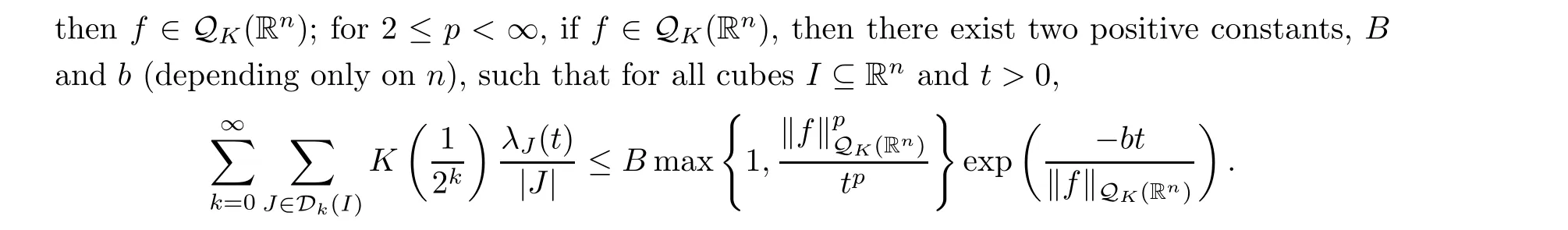
8.2 QK spaces of several complex variables
A Qspace on the unit ball Bof C, denoted by Q(B), was defined by Xu [85]. Some results for Q(B) can be found in [85, 86].
 Acta Mathematica Scientia(English Series)2021年6期
Acta Mathematica Scientia(English Series)2021年6期
- Acta Mathematica Scientia(English Series)的其它文章
- PREFACE
- PENALIZED LEAST SQUARE IN SPARSE SETTING WITH CONVEX PENALTY AND NON GAUSSIAN ERRORS*
- ENTROPICAL OPTIMAL TRANSPORT,SCHR¨ODINGER’S SYSTEM AND ALGORITHMS*
- NOTES ON REAL INTERPOLATION OF OPERATOR Lp-SPACES*
- HANDEL’S FIXED POINT THEOREM: A MORSE THEORETICAL POINT OF VIEW*
- Some questions regarding verification of Carleson measures
