Normal criteria for a family of holomorphic curves

The Montel theorem is also very useful in valued distribution. For example, the Montel theorem yields the Picard theorem and the Julia theorem. More generally, the three exception values in Theorem A can be extended to shared values.
Theorem B Let F be a family of meromorphic functions in a plane domain D. If there are three distinct points,a, a, a,in the Riemann sphere such that any two functions f,g ∈F share a, aand ain D, then F is normal.
This Montel-type theorem raises an interesting question about two families of meromorphic functions sharing some values. In 2013, Liu, Li and Pang ([7]) proved the following result:
Theorem C Suppose that F and G are two families of meromophic functions in a plane domain D. Let a,a,a,abe four fixed distinct points on the Riemann sphere. If for each f ∈F there exists g ∈G such that f and g share a,a,a,a, and G is normal in D, then F is normal.
In the 1950s, Wu ([14]) and Fujimot ([4]) began to study the normal family for holomorphic mappings and extended some classical results for meromorphic functions to holomorphic mappings. The notion of a normal family has proved its importance in geometric function theory in several complex variables. In recent years,as more and more attention has been paid to high dimensional complex analysis, the study of normal families of holomorphic curves and holomorphic mappings has become well developed. Many researchers,such as Aladro, Krantz,Ru, Tu and Pang, etc. have done much work on the normal family of holomorphic mappings and holomorphic curves (see, e.g. refs. [1, 8, 13, 15, 16]). In this paper, we will prove several theorems on the normality of holomorphic curves and holomorphic mappings.
We first give some definitions. Let P(C) be the complex projective space of dimension N; that is, P(C) = C-{0}/~, where (z,z,··· ,z) ~(w,w,··· ,w) if and only if(z,z,··· ,z) = λ(w,w,··· ,w) for some nonzero complex number λ. We denote by [z]the equivalent class of [z:z:···:z]. Suppose that
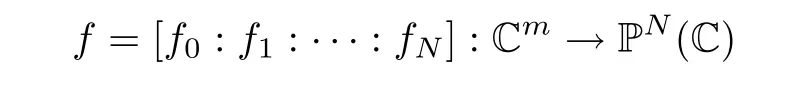
is a holomorphic mapping, where f,f,··· ,fare holomorphic functions of m variables. Denote by f = (f,f,··· ,f) a reduced representation of f if f,f,··· ,fhave no common zeros. The holomorphic mapping f is called a holomorphic curve when m=1. Letting D be a domain in C,we denote by H(D,P(C))the set of all holomorphic mappings f :D →P(C).
Definition 1.1 A family F ?H(D,P(C)) is said to be normal on D if any sequence in F contains a subsequence which is relatively compact;that is,if any sequence{f}?F contains a subsequence which converges to f ∈H(D,P(C)) uniformly on every compact subset of D.A family F is said to be normal at a ∈D if any sequence in F contains a subsequence which is relatively compact; that is, if any sequence of F contains a subsequence which converges compactly to f ∈H (D,P(C)) on some neighborhood Uof a.
If f ∈H (D,P(C))is representable as f =(f,f,··· ,f)with a polynomial(or constant)f, we say that f is rational (or constant, respectively). In particular, letting M be a domain in the complex plane, f : M →P(C) is a holomorphic curve which we denote by f ∈H(M,P(C)).

is a holomorphic function.
Definition 1.2 The multiplicity of holomorphic function 〈f,Q〉 at a point a is said to be the multiplicity of holomorphic mapping f intersecting Q at a.
Remark 1.3 It is easy to verify that the zeros in 〈f,Q〉 are independent of the choice of f. Hence, Definition 1.2 is well defined.
We denote f(Q) by
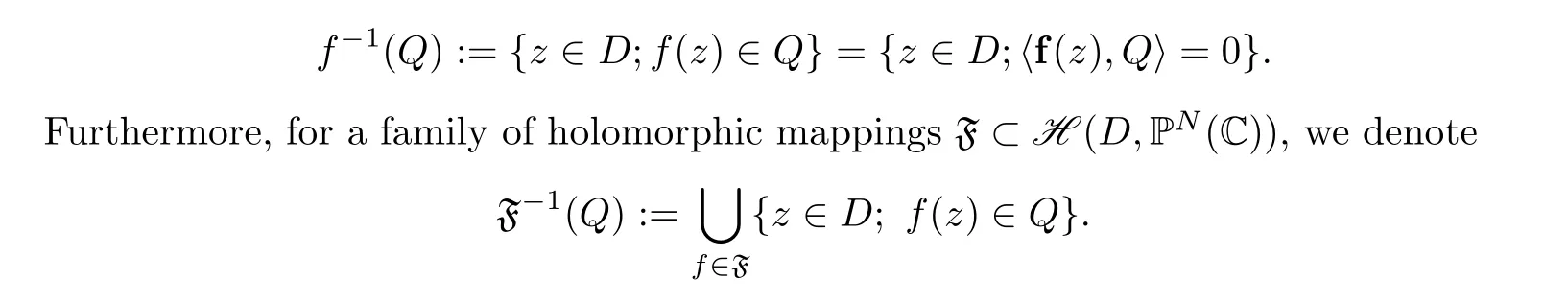
We then introduce the definition of a shared hypersurface, which is the extension of shared values for meromorphic functions.
Definition 1.4 Suppose that f, g ∈H(D,P(C)) and Q is a hypersurface in P(C).f and g are said to be sharing the hypersurface Q in D if
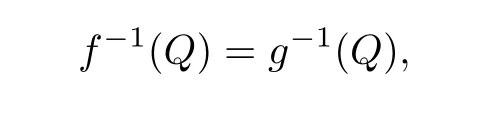
and is denoted by
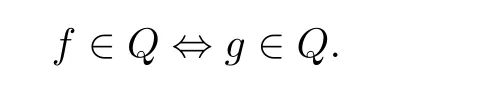
Furthermore, a family of holomorphic mappings F ?H(D,P(C)) is said to be sharing a hypersurface Q in D ?Cif, for any f ∈F, we have
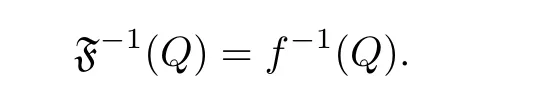
If H is a homogeneous polynomial of degree 1, we say that H is a hyperplane; that is,

where a∈C, 0 ≤j ≤N. We also denote by H = {〈z,α〉 = 0}, or α = (a,a,a,··· ,a),the hyperplane where 〈z,α〉 is the inner product of z and α. Similarly, we can define a family of holomorphic curves sharing hyperplanes. In particular, we say that holomorphic curve f is linearly degenerate if
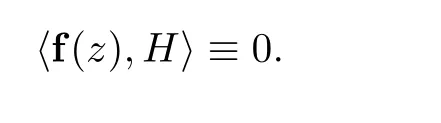
Otherwise, it is linearly nondegenerate. Throughout this paper, we use M, D, H and Q as a complex domain in C, a domain in C, a hyperplane and a hypersurface, respectively.
In 2014, Yang, Fang and Pang generalized Theorem B on a family of holomorphic curves sharing some hyperlanes; see [15].
Theorem D Let M be a domain in the complex plane. Suppose that F ?H(M,P(C))and H,H,··· ,Hare the 2t+1 hyperplanes located in t-subgeneral position,where t ≥N.If F shares H,H,··· ,Hon M, then F is normal.
In this paper, we will improve Theorem D. First, we will prove
Theorem 1.5 Let f be a holomorphic curve in a plane domain M, and let Q be a hypersurface in P(C). Then, either f(Q) is a discrete set in M, or f(Q)=M.
By Theorem 1.5, we can introduce the definition of a restricted hyperplane.
Definition 1.6 Let F ∈H(M,P(C)). A hyperplane H in P(C)is said to be restricted for F if, for any closed subset G ?M,
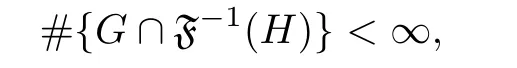
where # is the number of elements. H is said to be a general restricted hyperplane for F if there is a discrete set Esuch that, for any closed set G ?M, we have
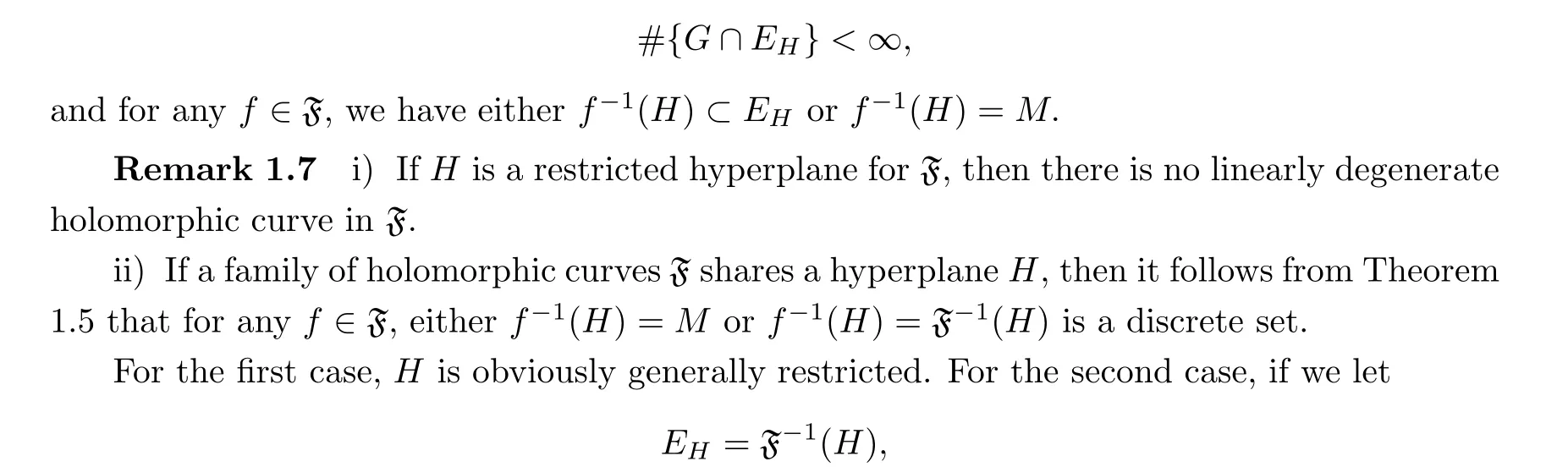
then H is restricted. Hence, in either of the two cases, H is generally restricted.
iii) A restricted hyperplane for F may not be a shared hyperplane and a shared hyperplane for F may not be a restricted hyperplane.
Based on the definition of a general restricted hyperplane, we prove the following,which is an extension of Theorem D:
Theorem 1.8 Suppose that F ?H(M,P(C)), where M is a domain in the complex plane. If for F there exist 2t+1 general restricted hyperplanes H,H,··· ,Hlocated in t-subgeneral positions, where t ≥N, then F is normal.
It follows from Definition 1.6 that a restricted hyperplane is also a general restricted hyperplane. Hence, we can also obtain the following result:
Corollary 1.9 Let F ?H(M,P(C)), where M is a plane domain. If for F there exist 2t+1 restricted hyperplanes H,H,··· ,Hlocated in t-subgeneral position, where t ≥N,then F is normal.
For the normality of two families of holomorphic curves, Yang, Fang and Pang generalized Theorem C and proved the following (see [16]):
Theorem E Suppose that F, G ?H(D,P(C)), where D is a domain in Cand Q,Q,··· ,Qare hypersurfaces located in t-subgeneral position, where t ≥N. If, for any f ∈F, there exists g ∈G such that f and g share Q(1 ≤i ≤3t+1) and G is normal, then F is normal.
We now introduce the definition of partial sharing.
Definition 1.10 Suppose that f, g ?H(D,P(C)), where D is a domain in C. For a hypersurface Q in P(C), f is said to be left sharing Q with g in D if f(Q) ?g(Q),denoted by
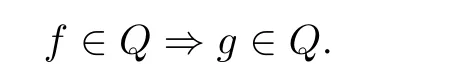
Remark 1.11 It follows from the definition that f ∈Q ?g ∈Q if and only if
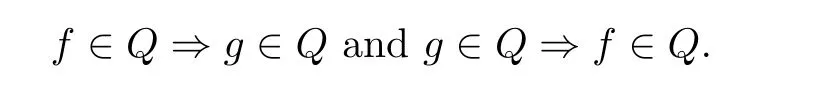
We will improve Theorem E and obtain the following result for holomorphic mappings:
Theorem 1.12 Suppose that Q,Q,··· ,Q?P(C) are hypersurfaces located in t-subgeneral position, where t ≥N. Let F, G ?H(D,P(C)), where D is a domain in C. If
i) for any f ∈F, there exists g ∈G such that for any j =1,2,··· ,3t+1, we have
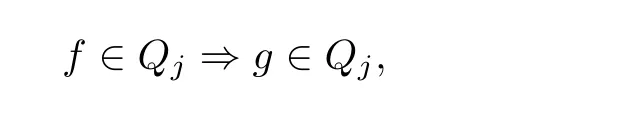
ii) G is normal,
then F is also normal.
2 Lemmas
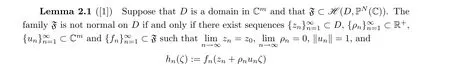
converges uniformly on compact subsets of C to a nonconstant holomorphic mapping h ∈H(C,P(C)), where ‖u‖ is the Euclidean length, and ζ ∈C satisfies z+ρuζ ∈D.
Lemma 2.2 ([15]) Suppose that f is a holomorphic curve,and that H, H, ··· , Hare hyperplanes in P(C)located in t-subgeneral position,where t ≥N. If,for each hyperplane H, j ∈{1,2,··· ,2t+1},and either〈f,H〉≡0 or〈f,H〉has finitely many zeros in C at most(no zero is allowed), then the map f is rational.
Lemma 2.3 Let f be a holomorphic curve. If there exist 2t+1 hyperplanes H, H, ··· ,Hin P(C) located in t-subgeneral position, where t ≥N, satisfying that
i) for each j ∈{1,2,··· ,s}, either 〈f,H〉≡0 or 〈f,H〉/=0, where s ≥t+1,
ii) for each j ∈{s+1,s+2,··· ,2t+1}, 〈f,H〉 has finitely many zeros in C at most,then f is a constant mapping.
Proof It follows from Lemma 2.2 that f is a rational mapping; that is, f is representable as f = (f,f,··· ,f) with polynomial f. Hence, 〈f,H〉 is a polynomial for each j =1,2,··· ,2t+1.

We know that s ≥N+1, hence if we choose other N+1 linear equations,we will have the same solution for the linear system. Anything else would contradict the uniqueness theorem of holomorphic functions.□
Lemma 2.4 ([16]) Let f ?H(C,X), where X is a closed set in P(C). If there exist 2t+1 hypersurfaces Q,Q,···,Qin P(C)located in t-subgeneral position,where t ≥N,such that either f(C)?Qor f(C)∩Q=?, then f is a constant mapping.
3 Proof of Theorems
3.1 Proof of Theorem 1.5
Let f =(f,f,··· ,f) be a reduced representation of f. Noticing that Q is a polynomial and that fis a holomorphic function, we can obtain that

is also a holomorphic function. Hence, either 〈f,Q〉(z)=Q(f,f,··· ,f)≡0,or its zeros are isolated. For the former, we have f(Q)=M. For the latter,we can conclude that f(Q) is a discrete set in M.
3.2 Proof of Theorem 1.8

It follows from Theorem 1.5 that for each f ∈F, f(H) is a discrete set. Since for all j ∈J His a restricted hyperplane, we have that Eis a discrete set, and there have been E.Furthermore, for any closed subset G ?M, we have

Hence, for any fixed point a ∈M, there exists a neighborhood Uof a such that the radius of Uis sufficiently small and
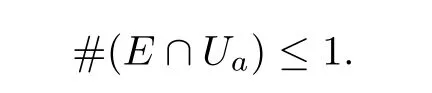
Then, for each f ∈F and H(1 ≤j ≤2t+1), there are only three possibilities:
1) f(U)?H; that is, for any z ∈U, we have 〈f,H〉≡0;
2) f(a) /∈H; that is, for any z ∈U, we have 〈f,H〉/=0;
3) f(a)∈H; that is, f(H)∩U={a}.
If we suppose that F is not normal at some a ∈M, then F is not normal in U. It follows from Lemma 2.1 that there exist sequences {z}?U, {ρ}?R, and {f}?F such that

converges uniformly to a nonconstant holomorphic curve h in any compact subset of C.
Next we will prove that for any j ∈J there are three possibilities: 〈h,H〉≡0,〈h,H〉/=0,or 〈h,H〉 has only one zero.
Let Hsatisfy 〈h,H〉/≡0 and {z ∈U; 〈h,H〉=0}/=?. If holomorphic function 〈h,H〉has two distinct zeros, then it follows from the Hurwitz theorem that when n is sufficiently large, holomorphic function 〈h,H〉 = 〈f(z+ρζ),H〉 has two distinct zeros. In other words, there are two distinct intersection points of fand H, which contradicts the definition of U. Therefore, 〈h,H〉 has only one zero.
Let
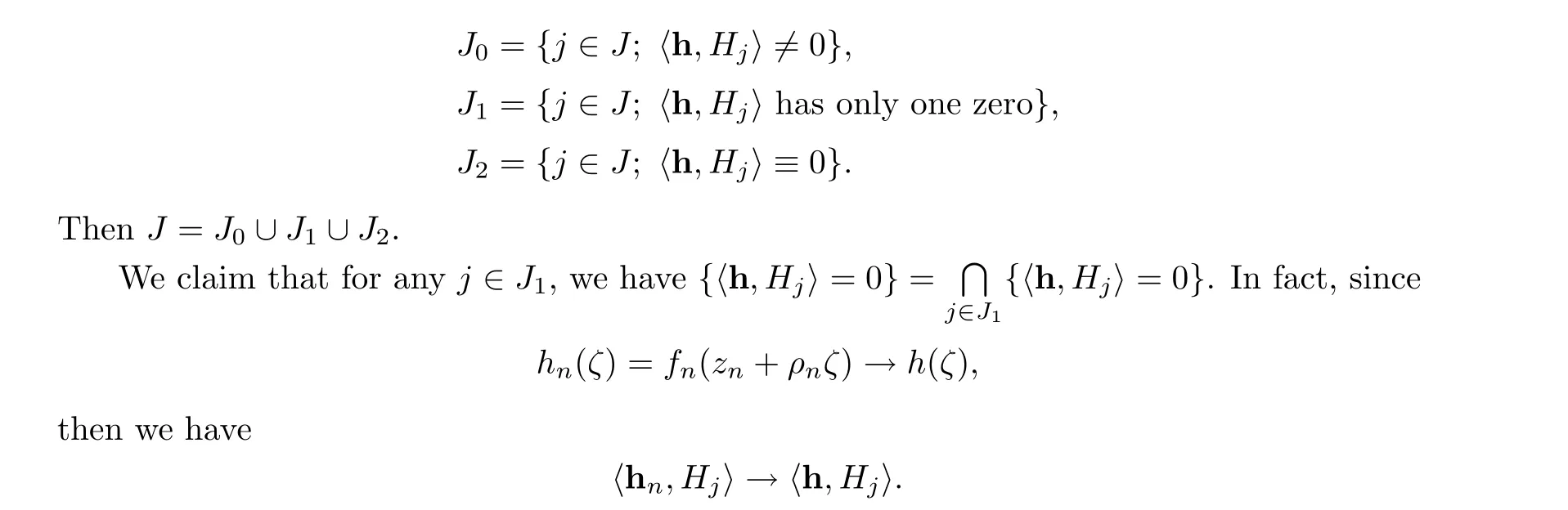
For any fixed j ∈J, if ζ∈C is a zero of 〈h,H〉 with multiplicity μ, where μ ≥1, then it follows from the Hurwitz Theorem that for ε >0, when n is sufficiently large, holomorphic function〈h,H〉has μ zeros in|ζ-ζ|<ε,counting its multiplicity. Therefore,we can choose a sequence ζ→ζsuch that when n is sufficiently large, we have z+ρζ∈Uand
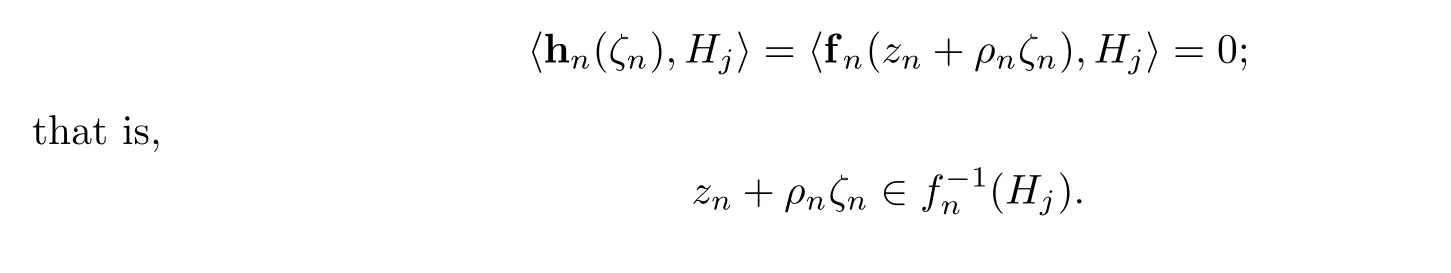

It follows from Lemma 2.3 that h is a constant mapping, which is a contradiction. By the arbitrariness of a and Definition 1.1, we can obtain that F is normal in D.
3.3 Proof of Theorem 1.12



Since jis arbitrary, there exist t+1 hypersurfaces Q, Q, Qsuch that 〈g(z),Q〉 = 0,which contradicts the hypothesis that Q,Q,··· ,Qis located in t-subgeneral position in X. Hence, Theorem 1.12 is true.
 Acta Mathematica Scientia(English Series)2021年6期
Acta Mathematica Scientia(English Series)2021年6期
- Acta Mathematica Scientia(English Series)的其它文章
- PREFACE
- PENALIZED LEAST SQUARE IN SPARSE SETTING WITH CONVEX PENALTY AND NON GAUSSIAN ERRORS*
- ENTROPICAL OPTIMAL TRANSPORT,SCHR¨ODINGER’S SYSTEM AND ALGORITHMS*
- NOTES ON REAL INTERPOLATION OF OPERATOR Lp-SPACES*
- HANDEL’S FIXED POINT THEOREM: A MORSE THEORETICAL POINT OF VIEW*
- Some questions regarding verification of Carleson measures
