Conformal restriction measures on loops surrounding an interior point
Yong HAN (韓勇) Yuefei WANG (王躍飛)


It is natural to consider a random connected subset of a simply connected domain that contains one given interior point, does not intersect the boundary, and satisfies some kind of conformal restriction property. To be more precise,let Ω denote the set of all connected closed subsets in the unit disk D that contain the origin, and whose complement is a topological annulus. Let F be the σ-algebra generated by the sets {K ∈Ω : O ?int(K)}, where O spans all the open sets of D. This σ-algebra is the same as the Borel σ-algebra induced by the Hausdorffdistance. Notice that for any simply connected domain D ?D with 0 ∈D, the set{K ∈Ω:K ?D} is measurable with respect to the above σ-algebra.
Now suppose that P is a probability measure on the measure space(Ω,F)that satisfies the following properties:
(i) (Rotational invariance) For any rotation Φ about 0, ΦP=P.
(ii) (Restriction property) For any simply connected domain D with a fixed point z ∈D,we can define Pas the image of P under any conformal map φ from D onto D with φ(0)=z.The restriction property is that for any simply connected domain D ?D with 0 ∈D, the conditional law of K on the event that K ?D is P, where K is the sample of P.
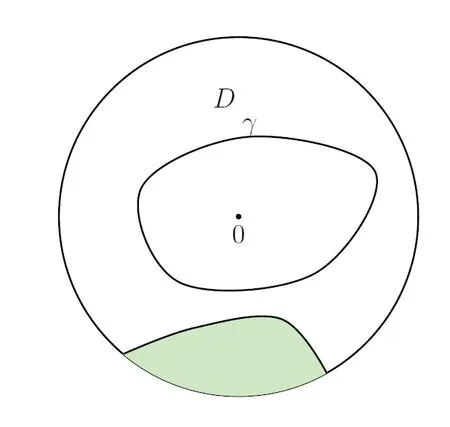
Figure 1 In this figure the simply connected domain D is the complement of the shaded area
We first state our main theorem.
Theorem 1.1 Suppose that P is a probability measure on(Ω,F) that satisfies the above two conditions. Then there exists a constant α >0 such that,for any simply connected domain D with 0 ∈D,


Remark 1.2 Notice that if a measure satisfies (1.1), then it satisfies the conformal invariance and restriction properties above. Since γ and K can be determined by each other, we will usually use γ instead of K when the context is clear.
Remark 1.3 We should note that γ in Theorem 1.1 is different from the loop γ(0),which is the loop surrounding 0 that is part of the conformal loop ensemble (CLE) defined in[11]. Recall that the (non-nested) CLE (see the detailed definition in Section 2 of [11]) is a collection of probability measures Pindexed by simply connected domains in the plane that satisfies conformal invariance and the restriction property. For a simply connected domain D,the sample of Pis a random family Γ = (γj ∈J) of non-nested simple disjoint loops in D.For any point z ∈D, there exists a loop in the sample of CLE contains z, almost surely. Thus,for the CLE in the unit disk,the restriction property implies that conditioned on the event that γ(0) ∈D ?D and the loops that are not contained in D, γ(0) has the same law as the loop~γ(0)of the CLE of the simply connected domain which is the connected component containing 0 of the set obtained by removing from D all the loops that are not contained in D. Therefore the loop γ(0) of the CLE in D depends on the information of other loops. The “restriction”property of γ(0) in CLE is different from the restriction property of γ in Theorem 1.1.
This paper is organised as follows: the second section,we give a brief introduction to radial Loewner equations and radial conformal restriction measures. The third section is devoted to the proof of Theorem 1.1. The relations between the radial conformal restriction measure and the properties of the loop measure are given in the last two sections.
2 Preliminaries
2.1 Loewner’s equation
Loewner’s equation was introduced by Loewner (see [8]) to prove part of the Bieberbach conjecture, which, since then, has been completely solved by De Branges (see [2]). In 2000,Oded Schramm(see [10]) found the “chordal”version of the Loewner equation and created the SLE (Schramm Loewner Evolution) theory to describe the scaling limits of many statistical physical models. Since then, SLE theory has proven to be an extremely powerful tool; for instance, it allowed Lawler, Schramm and Werner (see [6], [7]) to prove the famous conjecture of Mandelbrot about the a.s. dimension of the Brownian frontier.
In this section, in order to make this paper self-contained we give a very brief introduction to the radial Loewner equation.
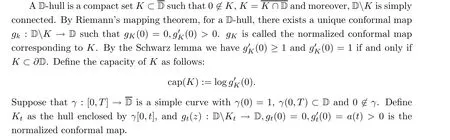

Lemma 2.2 (see Chapter 4 in [5]) Suppose that w(t) : [0,T] →R is a continuous realvalued function. Let λ(t)=eand let g(z) be the solution of the ODE (2.1). If Kand Dare as above, then
(1) for any t ∈[0,T], g:D→D is a conformal map;
(2) for any t ∈[0,T], Kis a D-hull;
(3) at z =0, g(z) has the Taylor expansion g(z)=ez+O(|z|).We call (g:0 ≤t ≤T) and (K:0 ≤t ≤T) the Loewner chain driven by w(t).
Remark 2.3 If λ(t) is only measurable continuous, we can still solve equation (2.1) to get a family of hulls.
2.2 Radial conformal restriction measure
We denote by Ω the collection of subsets of D that satisfies the following conditions:
(1) K is a connected closed set, K ∩?D={1};
(2) 0 ∈K and DK is connected.


3 Proof of Theorem 1.1
3.1 Proof of uniqueness
Here we present an argument similar to the one discussed in [1]. For r ∈(0,1), define f(r):=P(γ ?rD). According to the conformal restriction property, we have

3.2 Relation with the radial conformal restriction measure
In this section, we will show how we can construct a radial conformal restriction measure P(-α,2)from the conformal restriction probability measure P(α)(in Theorem 1.1)on the space of loops that surrounds 0 in D, provided that it exists. Motivated by this, we will construct P(α) from P(-α,2) in the subsequent section.


Then it follows that the hull enclosed by Φ(γ)is the radial conformal restriction P(-α,2). We have proved the following property:
Proposition 3.1 With above notations, Φ(γ) has the radial conformal restriction law P(-α,2), and Φ(γ) is independent of T.
Remark 3.2 In fact, we can choose any simple curve η from 1 to 0 and define


3.3 Existence
In this section, we will construct the conformal restriction probability measure on (Ω,F)in Theorem 1.1.

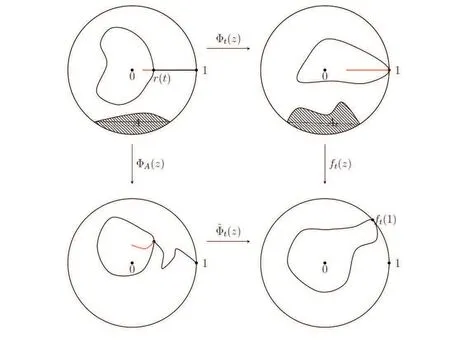
Figure 2 This figure shows the relations between Φt,ΦA(chǔ),~Φt and ft
so we have

In the first equation we used the definition of the radial conformal restriction measure in D[r(t),1).
Case 2 There exists tsuch that [r(t),1) ?A and [0,r(t))∩A = ?. Defining A:=Φ(A), we have

Here Pis the radial conformal restriction measure in D:= D[r(t),1), and in the fourth equation we have used the result of the first case.

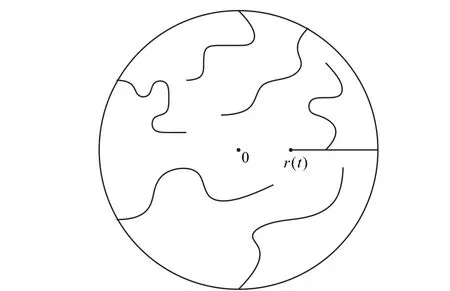
Figure 3 This figure shows a simply connected domain D in S which has the form
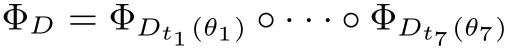
By the above two cases we have proven that for any simply connected domain D in S,Equation(1.1)holds. By the same discussion as for Proposition 4 of[12],we get that Equation(1.1) holds for any simply connected domain D ?D with 0 ∈D. This finishes the proof of existence.□
3.4 Another construction using the Brownian loop measure
In this section, we will give another construction using the Brownian loop measure. To keep this paper short and clear, we will not give the definitions and properties regarding the Brownian loop measure and the Poisson point process; these standard items can be found, for example, in the book [5].
By Proposition 3 in [12], we know that

Let γ denote the boundary of K. If we can show that, almost surely, γ lies in D, then the law of K just satisfies the conformal restriction loop law in Theorem 1.1.

Therefore we have proved that the conformal restriction probability with parameter α exists for all α >0.
3.5 Boundary is a simple loop
In this section, we show, using the same strategy as in Section 9 of [11], that the boundary of the conformal restriction probability measure is a simple loop . Let (γ)be a sample of the Poisson point process of the Brownian loops that surround 0 in D.
Let G be a graph whose vertices correspond to the loops (γ)and the edges of which correspond to those intersecting loops, i.e., v~vif and only if γ∩γ/= ?. Let T be a spanning tree of G. Relabeling if necessary,we may assume that the loops (γ)are ordered in such a way that for each k, the loop γhas one of γ,γ,··· ,γas a parent in T. Then for each fixed k, let ηbe the loop trace γ,γ,··· ,γwith a time parameter chosen such that it waits for a certain time at the point which is the intersection of two loops (for details, see Section 9 of [11]). Then, using a result similar to that of Lemma 9.6 in [11] (annulus-crossing property of the Poisson clouds of the Brownian loop measure surrounding 0), we see that ηconverges to a loop γ. From this, we conclude that the boundary of K constructed in the previous subsection is a simple loop.
4 Properties of the Loop Measure
In this section, we give some properties of the loop measure of Theorem 1.1.
4.1 Radius of the loop
Suppose that γ is a sample of the conformal restriction probability measure on simple loops.Denote
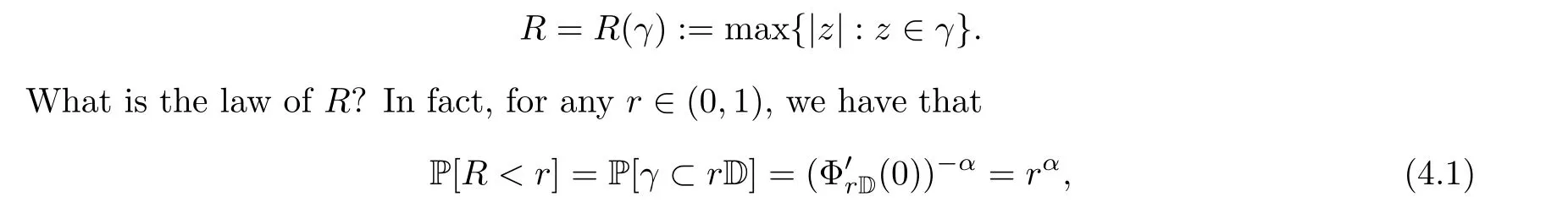
so R has the density function ρ(r)=αr.
Define E := {z ∈γ : |z| = R(γ)}. Another question is: is it true that #|E| = 1, almost surely?
By the properties of the Brownian loop measure, for any γin the Poisson point process,there is almost surely only one point that attains the maximal radius on γ. Thus if there are at least two points on γ that reach the maximal radius R(γ), there are at least two loops, γand γ, in the Poisson point process that have the maximal radius R(γ). This event happens with probability 0. This is because conditioned on the event R(γ) ∈(r -δ,r), the law of γ is the conformal restriction loop measure in rD conditioned upon γ /?(r-δ)D. We have the following analysis:

Proposition 4.1 Let R(γ)be the maximal radius of the conformal restriction loop sample γ in the unit disk. Then R has the density function ρ(r) = αrfor r ∈(0,1). Moreover,almost surely, there is only one point which is denoted by Z on γ that reaches the maximal radius R(γ). By the rotation invariance of γ, conditioned on the event that R(γ) = r, Z has the uniform distribution on |z|=r.decomposition of the law of γ:


In the second equation, we used the property of the radial conformal conformal restriction measure on rD with root eand exponent (-α,2). The map f(z) is the conformal map from rD[r,r) onto D with f(0) = 0. Thus (4.2) can be used to define the conformal restriction measure μ on self-avoiding loops.
4.2 The expectation of the area


 Acta Mathematica Scientia(English Series)2021年6期
Acta Mathematica Scientia(English Series)2021年6期
- Acta Mathematica Scientia(English Series)的其它文章
- PREFACE
- PENALIZED LEAST SQUARE IN SPARSE SETTING WITH CONVEX PENALTY AND NON GAUSSIAN ERRORS*
- ENTROPICAL OPTIMAL TRANSPORT,SCHR¨ODINGER’S SYSTEM AND ALGORITHMS*
- NOTES ON REAL INTERPOLATION OF OPERATOR Lp-SPACES*
- HANDEL’S FIXED POINT THEOREM: A MORSE THEORETICAL POINT OF VIEW*
- Some questions regarding verification of Carleson measures
