Correlated insulating phases in the twisted bilayer graphene*

Yuan-Da Liao(廖元達(dá)), Xiao-Yan Xu(許霄琰), Zi-Yang Meng(孟子楊), and Jian Kang(康健)

1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Department of Physics,University of California at San Diego,La Jolla,California 92093,USA

4Department of Physics and HKU-UCAS Joint Institute of Theoretical and Computational Physics,The University of Hong Kong,Pokfulam Road,Hong Kong SAR,China

5Songshan Lake Materials Laboratory,Dongguan 523808,China

6School of Physical Science and Technology&Institute for Advanced Study,Soochow University,Suzhou 215006,China

Keywords: twisted bilayer graphene,correlated insulator,quantum Monte Carlo simulation

1. Introduction

Since the discovery of correlated insulating phases and superconductivity(SC)in the twisted bilayer graphene(TBG)and other moir′e systems near the magic angle, significant progress has been achieved in understanding the properties of the electronic correlations in these systems.[1–74]The electron interaction in TBG is estimated as e2/(εLm)≈24 meV,where ε ≈4.4 is the dielectric constant of the hexagonal boron nitride(hBN)and Lm≈13 nm is the lattice constant of the moir′e superlattice. The bandwidth, estimated by first-principle calculations,is found to be less than 10 meV and thus smaller than the electron interactions,[1]suggesting that the system is either in the intermediate or strong coupling regime. While the weak coupling approach focuses on various instabilities that are enhanced by Fermi surface (FS) nesting and thus usually occur at incommensurate fillings,the correlated insulating states are observed only at commensurate fillings,[2,3,75]indicating that the electronic correlation in this system can be,at least,qualitatively understood with the strong coupling approach.

While early experiments produce the phase diagrams similar to those of heavy fermion and cuprates systems,[76]i.e.,with insulating phase, SC, and strange metal above the SC dome, the discovery of the quantum anomalous Hall (QAH)state at filling number ν =3 by aligning the system with the hBN substrates[70,71]reveals the uniqueness of TBG among other strongly correlated systems. Viewing from the itinerant perspective,the band calculations produce two Dirac cones at K and K′of the moir′e Brillouin zone(mBZ)for each valley.[1]Different from the graphene, the two Dirac cones have the same chirality, manifesting their non-trivial topological band properties.[23,31,77,78]As a consequence, this system is characterized by the interplay between the non-trivial topological properties and the strong interactions.

As schematically shown in Fig. 1, the two valleypolarized Dirac cones that have the same chiralities are protected by C2T symmetry, where C2is the two-fold rotation around the axis perpendicular to the graphene and T is the time-reversal symmetry. The two nodes have the same chirality as dictated by the two valley-polarized Bloch states at the momentum of M and these two Bloch states have the opposite parities under C2x, the two-fold rotation around ?x axis of Fig. 1(a). Although the topological properties are not protected by adding other remote topologically trivial bands and thus dubbed as“fragile”topology,the two same-chirality Dirac cones cannot be reproduced by any two-band tight binding models,leading to so called topological obstruction in such non-trivial topological systems. Especially, the C2T symmetry cannot be locally implemented with the Wannier states only for narrow bands.[77]Several approaches have been proposed to circumvent this difficulty, either by not locally implementing all the symmetries[20,21,23]or including several remote bands.[79]In this paper, the former approach is chosen,i.e., C2T is not locally implemented for the Wannier states,and then the associated Hamiltonian is constructed with the Coulomb interactions projected onto the narrow bands.

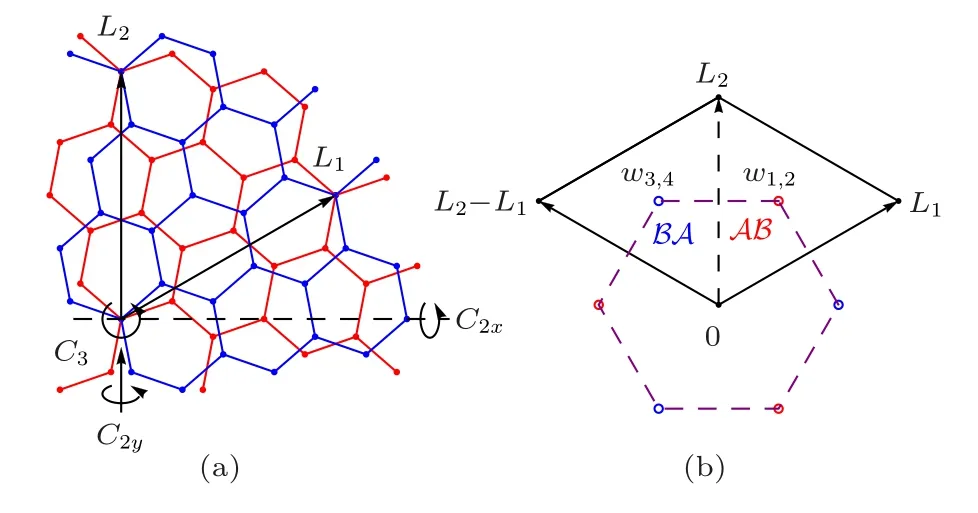
Fig.1. (a)The moir′e superlattice structure of the TBG.Blue(red)sites are the carbon atoms on the bottom(top)layers. The triangular lattice is formed when the twisted angle is commensurate. The plot shows the lattice when the twist angle θ =21.8?. Since the two-fold rotation C2x is not a symmetry transformation of the lattice, the symmetry group is D3. (b) The center of the local Wannier states. Black dots are the sites of the triangular superlattice. Red and blue dots are A? and ?A sites,respectively,where the local Wannier states centered. In our construction, w1 and w2 are placed at A?position, and w3 and w4 are placed at ?A position. Note that the A? and?A sites form an emergent honeycomb lattice. This figure is reproduced with permission from Ref.[20].

Although these Dirac cones are gapped by the interaction in the correlated insulating phases,the non-trivial topological properties are crucial to have a proper understanding of the mechanism and properties of the insulating phases. Different from the conventional Hubbard model, TBG lattice models constructed based on the above consideration would acquire extended interactions and actually give rise to the emergence of“ferromagnetic”states due to the mechanism similar to the quantum Hall ferromagnetism at the even integer fillings, including the charge neutrality point (CNP).[36,37,42,47,48,80,81]Furthermore,the kinetic terms lift the degeneracy of the interactions and favor the inter-valley coherent state.[36,47,81]While this order is at the momentum of q =0 and thus dubbed as“ferromagnetic”state,it does not couple to the external magnetic field,and therefore,qualitatively consistent with the experiments.

The strongly correlated moir′e lattice model constructed from the above principles cannot be solved analytically based on mean-field or perturbative approaches, instead, one needs to employ unbiased quantum many-body numerical calculations to achieve comprehensive understanding. Along this line, great progresses have been made from a constructive dialogue between the analytical and numerical communities.In particular, quantum Monte Carlo (QMC) simulations have been performed for carefully designed lattice models.[72,73,81]By implementing the fragile topology at the interaction level,one first starts with a two-band model with only spin degree of freedom but no orbital (valley) degree of freedom with cluster charge interaction on the hexagons,[72]the QMC simulation of this model gives rise to various translational symmetrybreaking insulating phases at CNP, for example, Kekule-type valence bond solid(VBS)phases.[82]Then with the valley degree of freedom taken into consideration, one can simulate a four-band model and investigate the interaction effect of the cluster charge repulsion upon the degenerated Dirac cones.[73]It is found that a continuous Gross–Neveu chiral O(4)transition happens between the Dirac cone and a VBS phase.Lastly,to fully incorporate the fragile topology in TBG,in particular the projection of the extended Wannier states onto the narrow bands, besides the cluster charge interaction,another assisted hopping interaction is introduced to the lattice model.[81]This turns out to be the crucial step of connecting the QMC model study with the realistic TBG experimental findings, as only with the assisted hopping on each moir′e hexagon, can the model gives rise to intervalley coherent (IVC) and quantum valley Hall(QVH)correlated insulating phases.

This review explains in detail how the aforementioned progresses have been made in stepwise manner. We start from the theoretical considerations on what is the proper real space moir′e lattice model of the TBG,and outline the possible correlated insulating phases suggested from the analytical calculation. Then we move on to the QMC simulation results on the lattice models inspired by the analytical considerations and follow the logic and technical flow of the numerical simulations to gradually provide the more relevant results in the ground state phase diagram at CNP.Towards the end,we will propose a few immediate directions that one can take from the results presented here and make new progress, for example,the ground state phase diagram of the other integer fillings and explain what is the proper and realistic numerical tools to tackle these difficult problems.

2. Model and phase diagram

2.1. Construction of Wannier states

In this section, we discuss the construction of the localized valley-polarized Wannier states (WS)s for the four narrow bands only. As explained above,the full symmetry of the Bitzritzer–MacDonald (BM) model[1]cannot be locally implemented because of the topological obstruction in the continuous model. To overcome this problem, we consider the discrete lattice model developed by Koshino et al.,[83]and set the twist center axis at the registered AA sites. As shown in Fig. 1(a), besides the time reversal symmetry, the symmetry group contains: i)the three-fold C3rotation symmetry around AA sites, ii) the two-fold rotation C2ythat interchanges the layer but not the sublattice,thus forming the D3group. Since C2zsymmetry is not contained in D3group,this model is free of topological obstruction and all the symmetry operations of the D3group and time reversal symmetry T can be locally implemented.

We start from the discrete lattice model developed in Ref.[83]

Solving the tight binding model in Eq. (1), we obtain four different narrow bands centered around the CNP. These four bands are separated from the remote bands by a band gap around 10 meV with the exact values depending on the twist angle. Although the lattice relaxation effect is important to reproduce the larger band gaps measured by the transport and STM experiments,[2,14]only quantitative difference is expected for the absence of this effect in our construction of WSs as our model includes only the narrow bands and the projected coulomb interaction. Each unit cell contains four constructed WSs, labeling as |wi,Rj〉, where Rjlabels the unit cell and i=1,...,4 labels the four WSs in each unit cell.

As the first step of our construction, it is crucial to identify the centers of the four WSs. One naive choice is to place them on the triangular moir′e superlattice sites. With this option,WSs transform as

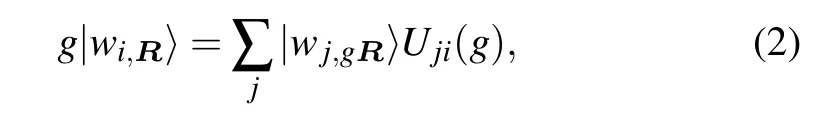
where g is a symmetry operation in the D3group,Rjspecifies the position of the triangular lattice, and gRjgives the new position of the lattice site after the symmetry transformation g. U(g) is a 4×4 unitary matrix that depends on g and describes the transformation of the WSs. We define the Bloch state ψi,kas the linear superposition of the WSs. Under the same symmetry operation g,we find

It is interesting to study the special case when the momentum is symmetry invariant,i.e.,Γ and K in the mBZ.We immediately conclude that the Bloch states should transform as U(g),and therefore, the Bloch states should transform in the same way at Γ and K. However, the Bloch states given by the discrete lattice model transform as two doublets at Γ but two singlets and one doublet at K. This proves that the symmetry of the Bloch states cannot be reproduced if all the WSs are placed at the sites of the triangular super lattice. Further analysis shows that the symmetry can be satisfied if the centers of WSs are placed at the honeycomb lattice sites,i.e.,the centers of the WSs|w1〉and|w2〉at A? and centers of|w3〉and|w4〉at ?A sites,as shown in Fig.1(b).

Once the positions of the WSs are determined,the method developed by Vanderbilt[84]is applied to construct the WSs,with details illustrated in Ref. [20]. Under time reversal T,|w1,2〉form a Kramer doublet,as well as|w3,4〉. Furthermore,under the symmetry transformation of the D3group,

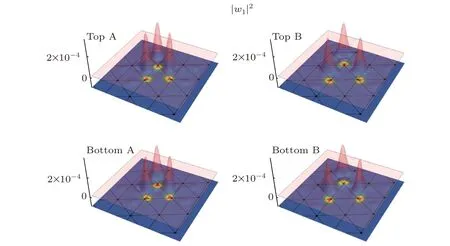
Fig.2. The localization of the WSs obtained from the projected method. The four panels show|w1|2 at(upper left)the top layer sublattice A, (upper right)the top layer sublattice ?, (lower left)the bottom layer sublattice A, and(lower right)the bottom layer sublattice ?. The figure is reproduced with permission from Ref.[20].

2.2. The projected Coulomb interaction

Having constructed the localized WSs for the narrow bands only, we project the coulomb interactions onto these WSs. As explained in Ref.[36],we numerically find that the interaction can be well approximated by

where A and ? are two different sublattices of the honeycomb lattice. We also emphasize that only the interaction is invariant under this SU(4)transformation. The whole Hamiltonian,after including the kinetic terms,breaks this SU(4)symmetry,and is only valley U(1)invariant.

Fig.3. The centers of the hexagons correspond to the triangular moir′e lattice spanned by primitive vectors L1,2. The Wannier state wavefunction centered on the moir′e honeycomb site(black dots)has three peaks at the neighboring triangular moir′e sites (colored disks). The overlap of two neighboring WSs are is shown schematically with red and blue colors.

It is worth to emphasize that this significant overlap comes from the non-trivial topological property of the narrow bands. If the narrow bands are topologically trivial, all the symmetries would be locally implemented for the WSs,including the two-fold rotation C2x. Consequently, the WSs would have the same parity under C2x,and thus,the two parts of the overlap between neighboring WSs would be the same since they are related by C2xsymmetry. Because the sum of the two parts must vanish, each part would also vanish. This leads to the cluster Hubbard model without any assisted hopping, as shown in HUin Eqs. (13)–(16). The crucial role of the assisted hopping terms will be thoroughly discussed in the next section by presenting the numerical results of models with three different types of interactions.

2.3. Honeycomb moir′e lattice models

Putting the above analytical considerations together and adding back the tight-bind part on a hexagonal superlattice,we can now construct the moir′e lattice model with interaction terms in the following pedagogical steps.

2.3.1. One orbital (valley) model

As discussed in our work Ref.[72],following the model suggested by Po et al.,[23]we proposed the following Hamiltonian to describe the subset of hole(or electron)bands of TBG:

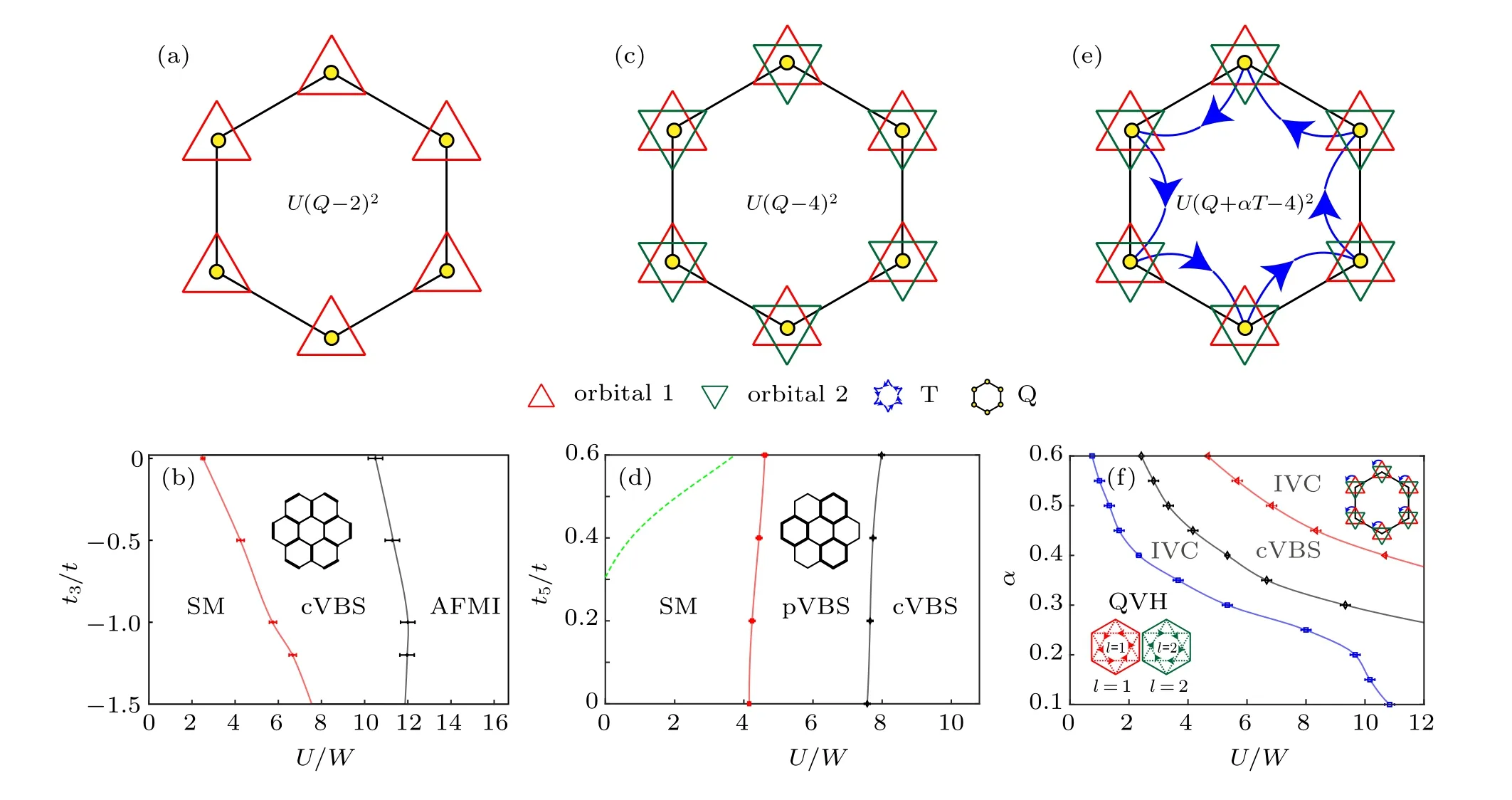
Fig. 4. Honeycomb moir′e lattice models of TBG and ground state phase diagrams at CNP obtained via QMC simulations. (a) Schematic representation of model described by Hamiltonian Eq.(13). Here,each lattice site on the moir′e honeycomb lattice contains one orbit(red triangles)and spins σ =↑,↓(not shown). The interactions act on every hexagon and consist of the cluster charge term Q(yellow dots). (b)Ground state phase diagram of(a),spanned by the U/W and third-nearest neighbor hopping-t3/t axes. The transition from SM to cVBS is continuous and belongs to chiral XY universality class. The transition from cVBS to AFMI is first order. (c)Schematic representation of model described by Hamiltonian Eq.(14). Here,each lattice site contains two valleys l=1,2(red and green triangles). (d)Ground state phase diagram of(c),spanned by the U/W and fifth neighbor hopping t5/t axes. The transition from SM to pVBS is continuous and belongs to chiral XY universality class. The transition from pVBS to cVBS is first order. (e)Schematic representation of model described by Hamiltonian Eq.(16). The interactions act on every hexagon and consist of the cluster charge term Q(yellow dots)and the assisted-hopping interaction term T(blue arrows). (f)Ground state phase diagram of (e), spanned by the U/W and α axes. The dash line at U =0 (y-axis) stands for the Dirac SM phase. At very small U, the ground state is a quantum valley Hall (QVH) phase characterized by emergent imaginary next-nearest-neighbor hopping with complex conjugation at the valley index,as illustrated by the red and green dashed hoppings with opposite directions. The system has an insulating bulk but acquires topological edge states. Upon further increasing U,an intervalley-coherent(IVC)insulating state is found,which breaks the SU(4)symmetry at every lattice site by removing the valley symmetry. Because it preserves the lattice translational symmetry,it is ferromagnetic-like. The columnar valence bond solid(cVBS)insulator,which appears after the IVC phase,breaks the lattice translational symmetry and preserves the onsite SU(4)symmetry.The phase transitions between QVH and IVC(blue line),between the IVC and cVBS(black line),and between the cVBS and IVC(red line)are all first order.

2.3.2. Two orbitals (valleys) model

In real TBG materical, there exists two valleys for the WSs, which requires a four bands model with both spin and valley degrees of freedom taking into consideration. In Ref.[73],we construct the following two-orbital spinful lattice model on a honeycomb lattice with cluster charge interaction:

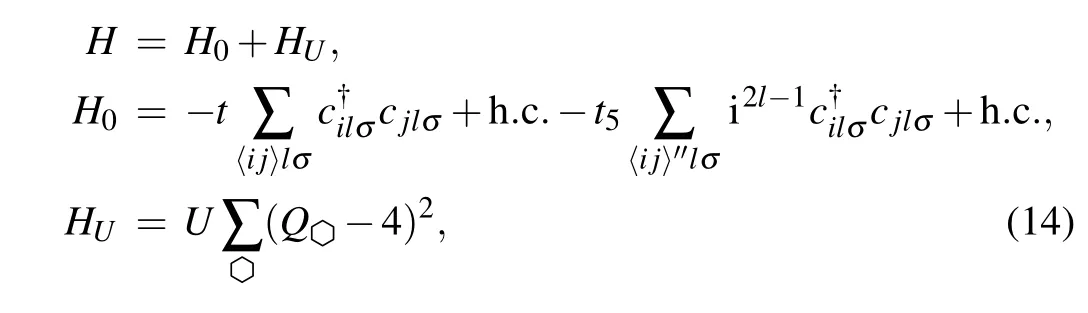
where orbital l=1,2 means the two valleys. The fifth neighbor hopping (it5for l = 1 and -it5for l = 2) is purely imaginary and breaks the orbital degeneracy along Γ–M direction in the high-symmetry path of BZ. H0is the tightbinding part introduced in Ref. [21] and serves as a minimal model to describe the low energy band structure of TBG with Dirac points at the CNP and band splitting along Γ–M direction. The Coulomb interaction term HUis the same as the model in Eq. (13), except that there are two orbits inside Q≡∑i∈,l=1,2(ni,l/3).

The QMC obtianed U/W–t5/t ground state phase diagram at half-filling is shown in Fig.4(d). We also found three phases in total—they are semimetal (SM) phase, a plaquette valence bond solid(pVBS)phase,and a columnar valence bond solid(cVBS)phase.The two VBS are gapped insulators.Furthermore, the transition between SM and pVBS is continuous,and the phase transition from pVBS to cVBS phase appears to be first order,as will be explained in Section 3.

2.3.3. Two orbitals (valleys) model with assistedhopping term

As discussed in Subsection 2.2, microscopically, the full interaction of the lattice model can be derived from projecting the screened Coulomb repulsion on the narrow WS of TBG.Such projection leads to the emergence of an additional and sizable non-local interaction, of the form of an assistedhopping term,[36,61]as shown in Eqs.(10)and(12). As aforementioned,this new interaction ultimately arises from the nonlocal implementation of the C2T symmetry in a lattice model,such that the Wannier obstruction[23]can be overcome at the strong coupling limit. Therefore,the assisted-hopping interaction is not a simple perturbation,but a direct and unavoidable manifestation of the non-trivial topological properties of TBG.

As shown in Fig. 4(e), our model describes two valleys(orbitals)of spinful fermions on the honeycomb lattice that is dual to the triangular moir′e superlattice. The Hamiltonian is given below:

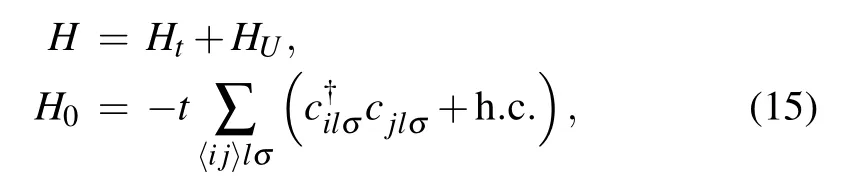
3. Numerical results

In this section,we present the unbiased QMC results for the moir′e lattice models in Section 2.

In the inset of Fig.4(b),we present the cVBS order in real space on honeycomb lattice. It breaks the lattice translational symmetry, and the broken symmetry is Z3, which will result in a signal in momentum space. To detect the signal of cVBS order,We can define a bond-bond correlation structure factor

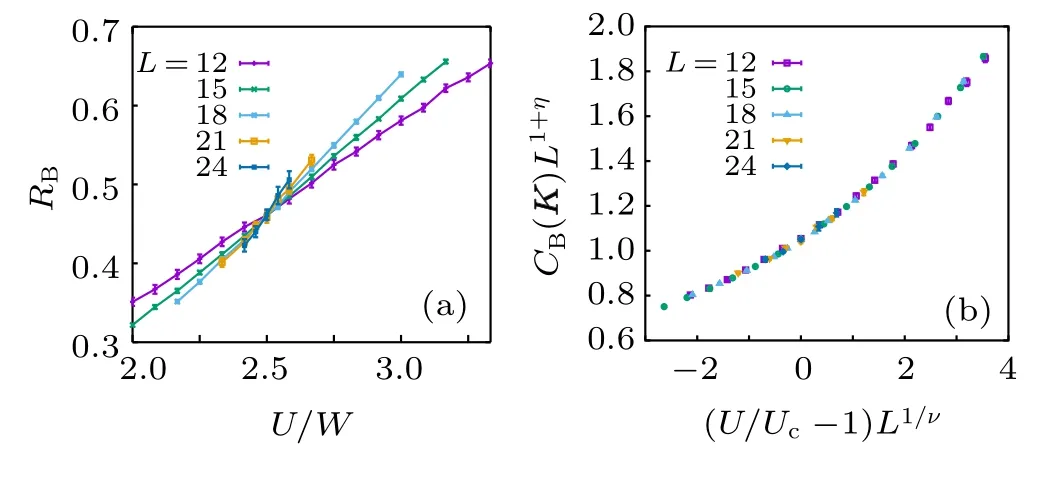
Fig.5.(a)Correlation ratio of the bond correlation for t3/t=0.The crossing point gives an estimate of the critical point Uc/W =2.50(3). (b)Data collapse of bond structure factor at momentum K,which is the absolute value squared of the cVBS order parameter. The transition from SM to cVBS belongs to chiral XY universality class. The data collapse gives ν =1.05(5),η =0.76(2). The figure is reproduced with permission from Ref.[72].

We further collapse the cVBS structure factor near the QCP with a finite size scaling relation CB(K,U,L)Lz+η=fB((U/Uc-1)L1/ν), here we set the exponent z=1 because of Lorentz symmetry. This process can collapse all data points at one single unknown curve, as shown in Fig. 5(b). We can obtain the critical exponents ν = 1.05(5) and η = 0.76(2),which are comparable with the QMC results on different models.[82,85–90]

Fig.6. (a)The ratio between structure factor of AB staggered spin correlation at momentum Γ and structure factor of bond correlation at momentum K. The sharp jump is one evidence that cVBS to AFMI transition here is first order. (b)Kinetic energy per site of the system. Again the kink in the kinetic energy with tuning parameter U is another evidence of first order transition. The figure is reproduced with permission from Ref.[72].

The pVBS and cVBS share the same order parameter.For the two-orbital model in Eq. (14), we follow the same methodology of the one orbital model to study the SM–pVBS

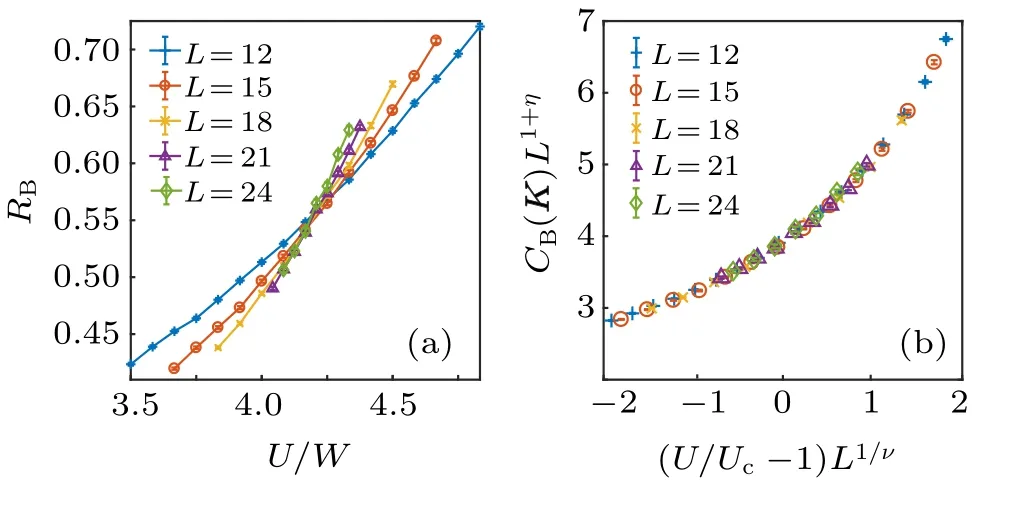
Fig. 7. (a) The bond–bond correlation ratio RB and (b) data collapse analysis of structure factor CB(K) at t5/t = 0 as function of U/t with L=12,15,...,24. The crossing of RB in (a) gives the DSM–pVBS critical point Uc/t =25.1(2). The data collapse in (b) gives the 3D N =4 Gross–Neveu chiral XY exponents η =0.80(2),ν =1.01(3). The figure is reproduced with permission from Ref.[73].

Similar with the one-orbital model,if we further increase U/W from the pVBS phase,we will observe a kinetic energy kink at U/W ≈7.67,as shown in Fig.9(a). At the same interaction strength U/W ,there is also a kink of the VBS correlation,as shown in Fig.9(b). These results indicate that,a first order phase transition appears at UVBS/W ≈7.67 between two different VBS phases. There are three non-equivalent VBS configurations,[85]but only two of them,the pVBS and cVBS,will broke the translational symmetry. In view of the fact that the translational symmetry has been broken in these two VBS phases, the phase transition observed in Figs. 9(a) and 9(b)could be the transition between pVBS and cVBS phases.

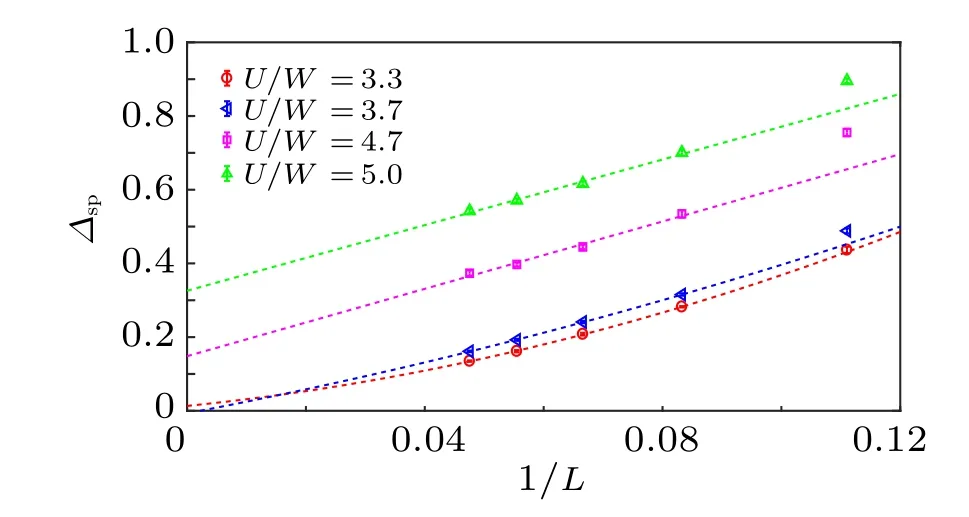
Fig. 8. (a) The 1/L extrapolation of single-particle gap Δsp(K), the gap opens between U/t =22 and U/t =28, consistent with the Uc/t obtained from the bond correlation ratio in Fig. 7(a). The figure is reproduced with permission from Ref.[73].

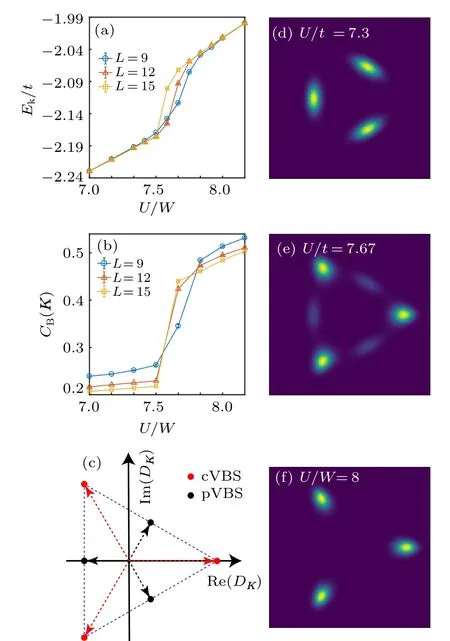
Fig.9. (a)Kinetic energy per site of the system for U at large values. The sharp jump signifies a first order transition. (b)CB(K) for the same process, a jump in VBS order is also observed, suggesting this is a transition between different VBS phases. (c)Angular dependence of the complex order parameter DK.Black dots represent ideal pVBS order,and red dots represent ideal cVBS order. (d)–(e) Histogram of DK at different interaction strengths U ＜UVBS,U ≈UVBS, and U ＞UVBS. The figure is reproduced with permission from Ref.[73].

Naturally, the cross-term of the interaction will induce an imaginary hopping between next-nearest-neighbors when the interaction strength is relatively small. Consequently, the mean-field Hamiltonian becomes two copies(four,if we consider the spin degeneracy) of the Haldane model,[101,102]resulting in an insulator with Chern number of ±1 for the two different valleys. Note that a Chern number can be defined separately for each valley l=1 and l=2(with spin degeneracy). Because the valley U(1)symmetry guarantees that these two Chern numbers must be identical, the whole system is characterized by one Chern number that takes integer values,i.e., it belongs to a Z classification.[103]Due to that, we call this state as QVH phase; it is illustrated in the corresponding inset in Fig.4(f).

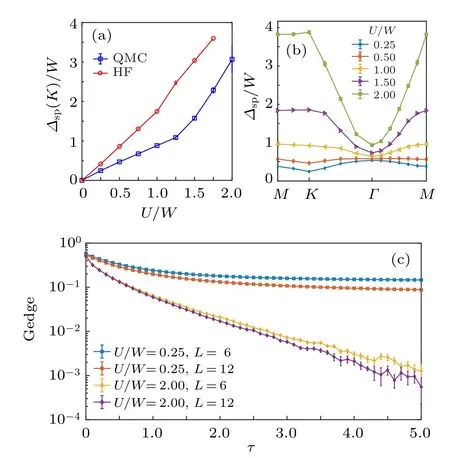
Fig.10. Quantum valley Hall insulator(QVH)and gapless edge states. (a)The single-particle gap Δsp(K)/W at the K point as a function of U/W for α =0.45,extracted from both QMC(blue points)and HF calculations(red points). For QMC,the spatial system size is L=12. The Dirac semi-metal is gapped out at the smallest small U values probed. (b)Single-particle gap extracted from QMC with L=12 along a high-symmetry path of the Brillouin zone. (c) The topological nature of the QVH phase is manifested by valley-polarized edge states. Here we compare the edge Green’s function for valley l =1 and spin ↑at U/W =0.25 (inside the QVH phase) and U/W =2.0(inside the IVC phase). It is clear that gapless edge modes only appear in the former case, highlighting the topological nature of the QVH phase. The figure is reproduced with permission from Ref.[81].

It is known that there are gapless edge modes in the Haldane model, despite the bulk being gapped. Form the above theoretical analysis,these edge states should be valleypolarized in the QVH phase. To verify that, we performed QMC simulations with open boundary conditions and extracted the imaginary-time Green’s functions on the edge,Gedge(τ)～e-Δspτ. As shown in Fig.10(c),the Green’s function on the edge decays to a constant in the long imaginarytime limit at small U (U/W =0.25), the gapless edge mode disappears when increasing U (U/W = 2.0), in agreement with the theory very well. It is an important progress that the associated-hopping term qualitatively changes the ground state, as compared to the above two-orbit model only with Hubbard cluster interaction.

It is clear that,as U/W increases,in both cases the ground state evolves from QVH to IVC to cVBS and then back to IVC.Furthermore, as will be discussed in Section 4, in the strong coupling limit U/W →∞, the IVC order CI(k=0) is independent of α and saturates at 0.5. As shown in Fig. 12, our QMC results also confirm such expectation.

It is worth to emphasize that various translation symmetry breaking phases also appear in the numerical studies based on the continuum model. For example, recent density matrix renormalization group(DMRG)studies based on hybrid Wannier states have revealed a stripe phase, depending on the parameters of the BM model,which may strongly compete with the QAH state at the odd fillings.[61,104]In addition, the exact diagonalization(ED)based on the Bloch states also found various stripe and charge density wave (CDW) phases with the wavevector of M or K.[105]Such translation symmetry breaking phases obtained by all these numerical studies, including our QMC calculation on Wannier states,establish the uniqueness of the TBG system distinguished from quantum Hall physics.

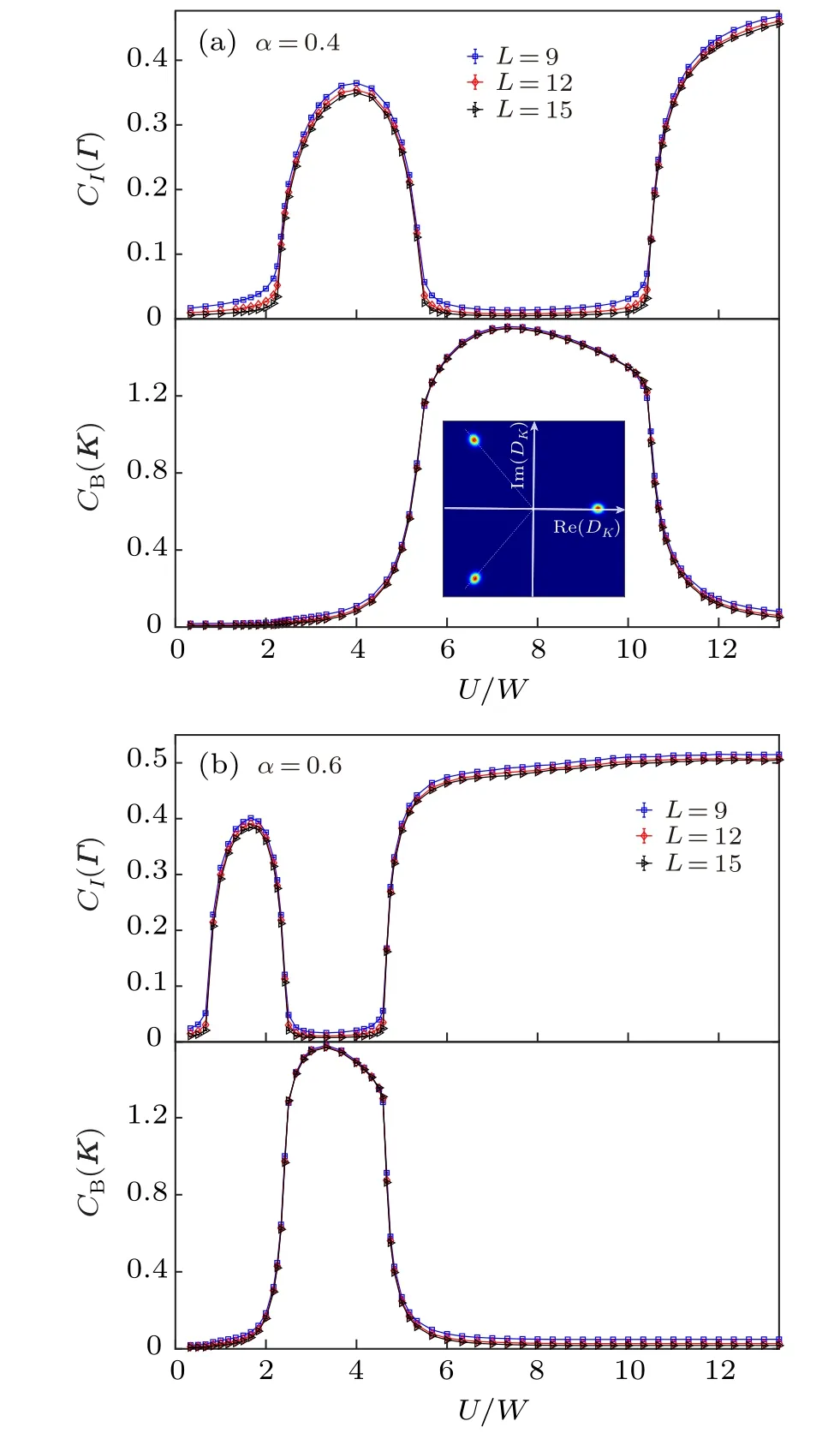
Fig. 11. Intervalley coherent (IVC) and columnar valence bond solid(cVBS)insulating states. Correlation functions CI(Γ)and CB(K),indicative of IVC and cVBS orders, respectively, as a function of U/W for (a) α =0.4 and (b) α =0.6. Linear system sizes are indicated in the legend. In both panels, the QVH–IVC transition, the IVC–cVBS transition,and the cVBS–IVC transition are all first-order. The inset in panel (a) presents the histogram of the complex bond order parameter DK at U/W ～5.3. The positions of the three peaks are those expected for a cVBS phase, instead of a pVBS state. The figure is reproduced with permission from Ref.[81].

Fig. 12. The CI(Γ) and CB(K) as a function of α at the strongcoupling limit. We perform the QMC simulation with projection length Θ=200L,interval of time-slice Δτ=0.1,spatial system sizes L=9,12,and setting U =1 as a dimensionless constant. The corresponding correlation function CI(Γ) of IVC is close to the saturation value of 0.5.And the correlation functionCB(K)of cVBS is close to 0,which means that cVBS disappears at the strong-coupling limit. The figure is reproduced with permission from Ref.[81].

4. Analytical results in the strong coupling limit

4.1. H0=0

In the case of zero kinetic energy, the manifold of the ground states is described by Eq. (19). To compare with the numerical results produced by QMC,we consider the correlation function

4.2. Strong coupling limit

In this subsection, we assume that H0is finite but small compared with H. Since the kinetic terms break SU(4)symmetry, the ground state manifold shrinks and not every unitary matrix U in Eq.(19)gives the ground state. Our purpose here is to identify the new manifold of the ground states and show that it is independent of the exact form of kinetic terms as along as they breaks the SU(4)symmetry described previously.

For the convenience of calculation, we write Eq. (19) in the following form:

5. Discussion

This paper reviews the real-space lattice model construction and solution of the TBG systems and in particularly focuses on the strong coupling limit where the interactions are more important than the band structure. We first briefly explain the topological properties of the TBG material,and outline ways to circumvent the topological obstruction to construct the localized Wannier states that give rise to the narrow bands.Based on these considerations,we project the Coulomb interactions onto the narrow bands and obtain both cluster charge and assisted hopping terms as interactions in the hexagonal moir′e lattice. We then move on to the unbiased QMC solutions of such model at CNP and summarize in a three-stage manner the phase diagrams obtained as we gradually increase the band numbers and the level of complexity in the interactions and therefore making the obtained phases more realistic and relevant with the experiments. In the strong coupling limit, the Hamiltonian at the CNP can be exactly solved and the solution is highly consistent with the QMC results.

Our theoretical analysis and quantum many-body computation reveal the crucial role of the topological properties even in the strong coupling regime. In contrast to most strongly correlated system where the translation symmetry is usually broken,such non-trivial topological features and the strong interactions lead to the rise of the “ferromagnetic” orders with q=0 in the TBG,or more generally,in other graphene based moir′e systems. It is interesting to see from our QMC numerics, that once the assisted hopping interaction is added to the two-orbital model, the IVC phase which breaks the SU(4)symmetry but at the same time stays at q = 0 is favored,amended with a QVH insulator which is symmetric and acquires a non-trivial Chern number.These phases are consistent with the analytical expectations and are the very reasonable candidates for the insulating phases discovered in the TBG at even integer fillings,in particular at CNP.

As a starting point to study the interplay between the nontrivial topological properties and the strong interactions in the electronic systems,our work provided a rather novel perspective to understand the properties of the electronic correlations.Although most of the work in this field focus on the ground states only, our numerical work also obtained the dispersion of charged excitations. It is interesting to compare this result with the STM and future ARPES experiments for more quantitative justification of our model.[11,13,14,106,107]

Looking forward, here we have only revealed the QMC numerical data on the honeycomb moir′e lattice models for TBG, and the QMC simulation is limited at CNP due to the sign problem. Another powerful method, density matrix renormalization group (DMRG), is tremendously successful in studying the low dimensional system.[108]Recently, it was applied to study the interacting BM model without the spin and valley degrees of freedom.[61,104]At the half filling where the system contains one fermion per unit cell, the numerics has identified three competing phases: QAH, strongly correlated topological semimetal,and the gapped stripe phase. While the first one breaks C2T symmetry and leads to quantized Hall conductivity, the latter two phases are C2T symmetric with vanishing Hall conductivity. Although based on the simplified model and focusing only on the filling of ν =1, DMRG already produced unexpected results beyond any mean field calculations. One can expect that more sophisticated DMRG calculations and its possible combination with QMC by including spin and valley degrees of freedom and various dopings and accessing larger system sizes for the thermodynamic limit,the more complete understanding of the electronic correlations and physical mechanism behind the insulating phases,correlated metallic phase,and eventually the superconducting phase in moir′e TBG systems can be finally achieved.

Acknowledgements

We thank Oskar Vafek, Rafael Fernandes, Clara Brei?,Brian Andersen, Chen Shen, Guangyu Zhang, Vic Law, Xi Dai, and Patrick A. Lee for the useful conversation and constructive collaborations over the projects that have been summarized in this paper. YDL and ZYM thank the Center for Quantum Simulation Sciences in the Institute of Physics,Chinese Academy of Sciences,the Computational Initiative at the Faculty of Science and the Information Technology Services at the University of Hong Kong,the Platform for Data-Driven Computational Materials Discovery at the Songshan Lake Materials Laboratory,and the National Supercomputer Centers in Tianjin and Guangzhou for their technical support and generous allocation of CPU time.