Breakdown point of penalized logistic regression*
DONG Yulin, GUO Xiao
(International Institute of Finance, School of Management, University of Science and Technology of China, Hefei 230026, China)
Abstract Breakdown point is regarded as an important measure of robustness in regression analysis. At the same time, sparse model estimation is a hot topic in data analysis. In the case of less attention to the breakdown point of robust estimates in nonlinear models, we study it in binary response models. We prove that the penalized estimate of logistic models always stays bounded, which means the finite explosive breakdown point of it is 1. Moreover, we give an upper bound of the implosive breakdown point of the slope parameter. Both simulation study and real data application verify this point while we use the approximation method and coordinate descent algorithm.
Keywords breakdown point; logistic regression; maximum likelihood estimator; penalization; robust estimation
Breakdown point is one of the basic tools to measure the robustness of statistical estimation. It was firstly defined by Hample[1], depending on the specific distribution of the observed data set. A distribution-free finite-sample definition of the breakdown point was proposed in Ref.[2]. Intuitively, the breakdown point is the maximum proportion of outliers that a given sample may contain without spoiling the estimator completely. Obviously, higher breakdown point indicates more robustness of an estimator. This concept has been widely applied to the location, scale, and regression models to describe the resistance of outliers.
The study of breakdown point has made great progress over the recent 40 years. In linear regression models, it is well known that the breakdown point of least square method is 0, which means only one outlier may have a large effect on the estimator. Robust estimators with a high breakdown point of 0.5 have been developed, e.g. the MM-estimators[3], the τ-estimators[4]; the least median of squares (LMS) and least trimmed squares (LTS) estimators[5]. The breakdown properties of some nonlinear regression model estimators were also investigated in, e.g. Ref.[6]. In the area of logistic regression model, the breakdown property of the maximum likelihood estimator (MLE) is totally different from that of the linear model. Cox and Snell[7]argued that the commonly used MLE in logistic regression models is not robust. Christmann[8]proposed that high breakdown point estimators do not exist in logistic regression models, unless there are some specific conditions, such asp≤n. Similar statement was noticed by Ref. [9] if one replaced some observations to raw data set. Neykov and Muller[10]considered the finite-sample breakdown point of trimmed likelihood estimators in generalized linear models. Khan et al.[11]adopted the least trimmed absolute (LTA) estimator for logistic model fitting, in which LTA is a robust estimator with high breakdown since it outperforms M-estimator in case of a certain degree of contamination. Croux et al.[12]proved that classical MLE in logistic regression models always stays bounded if some outliers were added to the raw data set. However, the aforementioned methods requires low-dimensionality thatn>p.
Due to the rapid development of science and technology and various ways of data collection, large-dimensional data is becoming more and more common and has attracted great attention. Regularization is powerful to solve high-dimensional problems, which can force the model be sparse, low rank, smooth and so on. Thus, a lot of penalized estimators have been established to select useful variables for high dimensional statistical linear modeling. Breiman[13]proposed the nonnegative garrote for subset regression. Tibshirani introduced lasso in Ref. [14], and LAD-lasso was discussed in Ref. [15]. Xie and Huang[16]applied the smoothly clipped absolute deviation (SCAD) penalty to achieve sparsity in the high-dimensional linear models. Therefore, breakdown point of penalized regression is becoming more important. Alfons et al.[17]focused on some sparse estimators in linear models, in which the breakdown point of sparse LTS is verified to be (n-h+1)/n, wherehis the initial guess of non-contaminations, both lasso and LAD-lasso have the breakdown point of 1/n. Various penalized logistic regression estimators are also proposed as alternatives to the non-robust MLE in logistic models, but the breakdown point of penalized logistic regression model under high-dimensionality is not discussed yet. It can neither be derived from the results of the penalized linear model nor from the generalization of the results of the unpenalized logistic regression models.
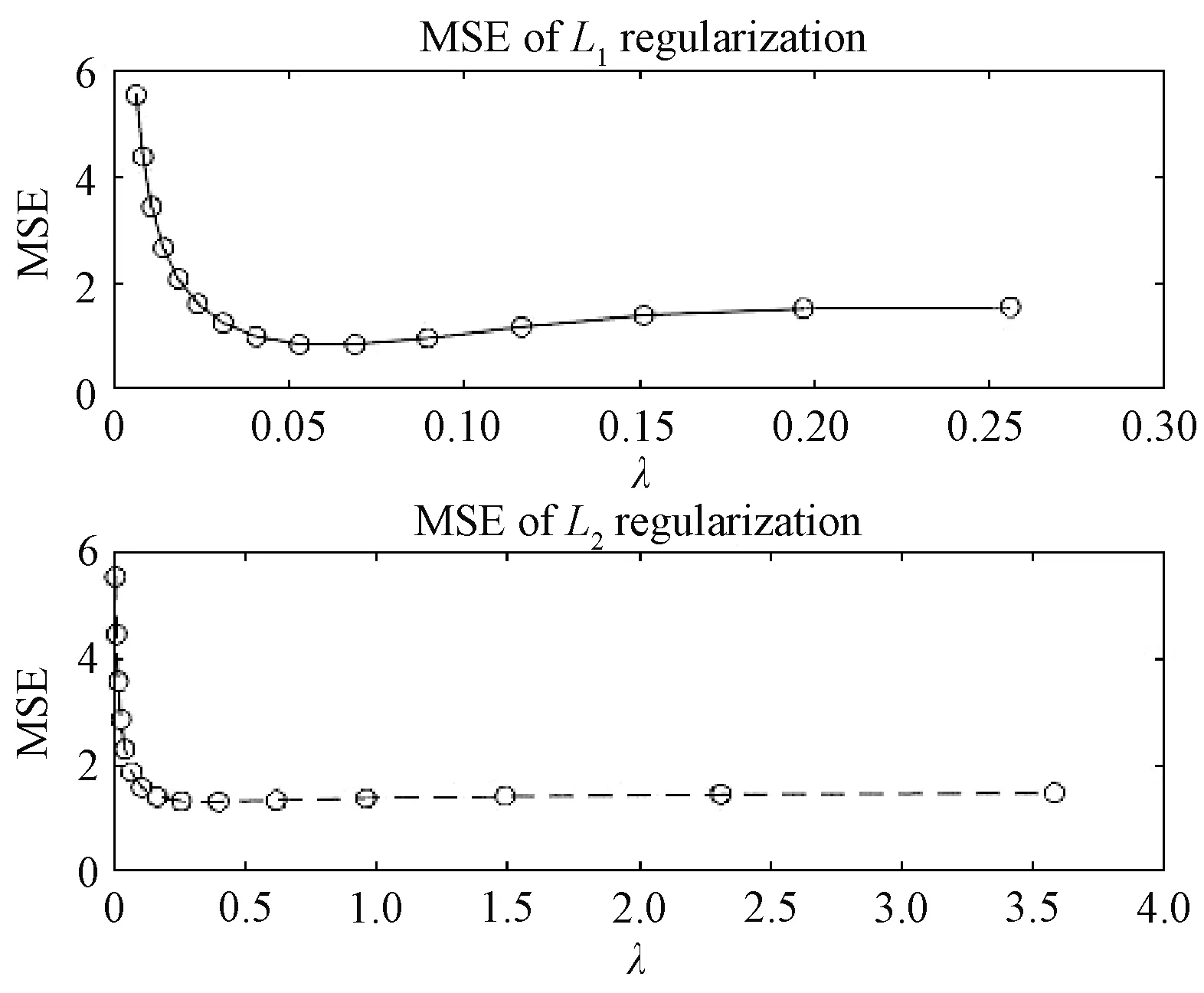
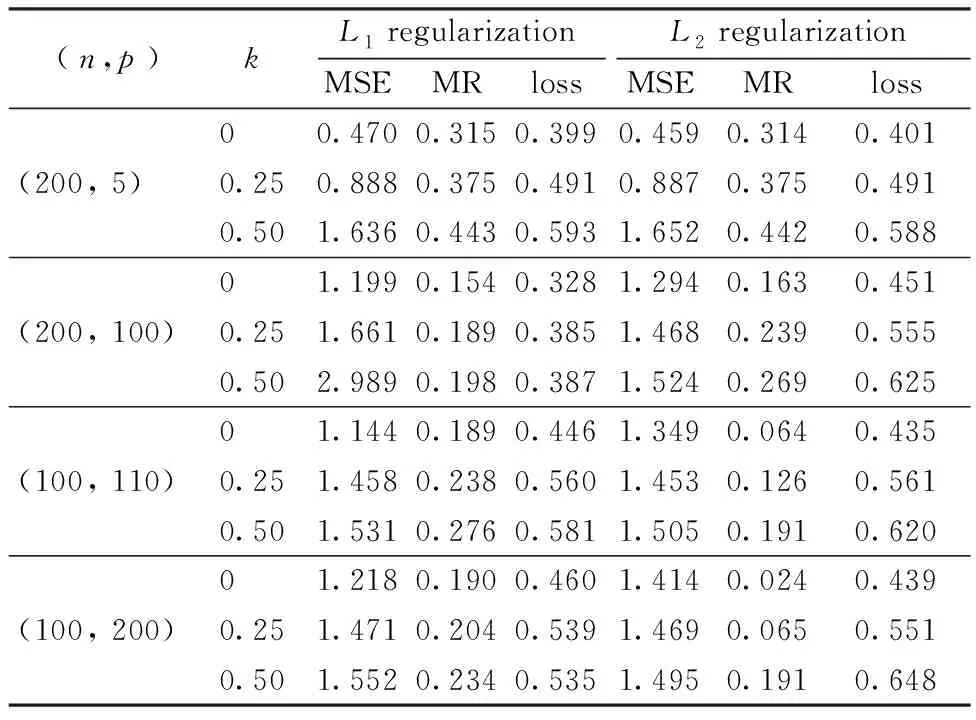
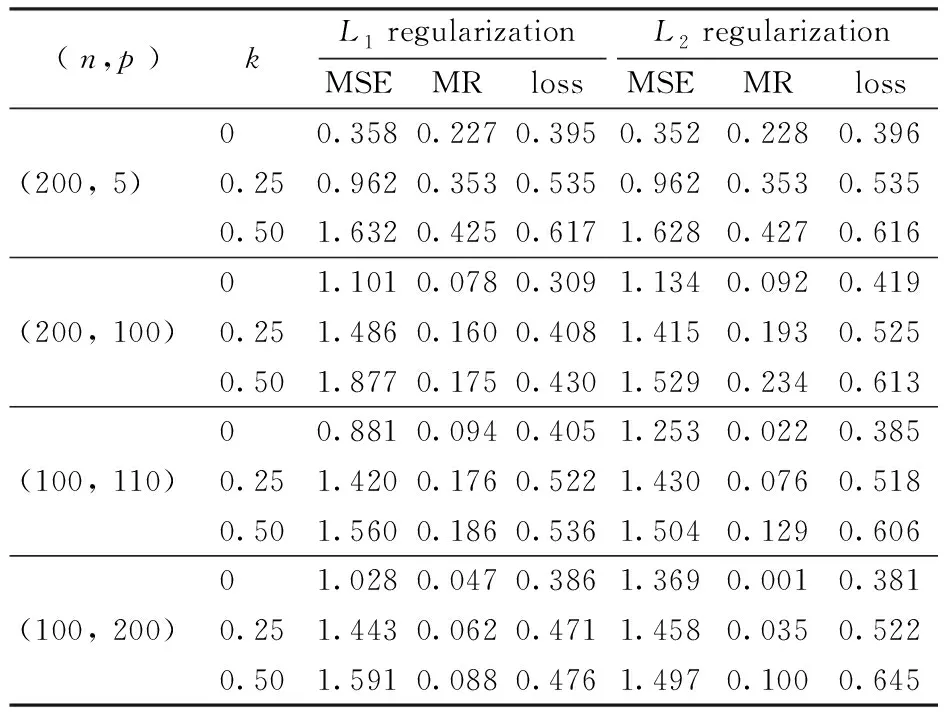
We aim to compute the breakdown point of penalized logistic regression estimator while there are outliers in the observations. Traditional methods are often limited ton>p, but the collected data sets are often with sophisticated large scale, so we emphasis not only onn>p, but also onn The rest part of this article is arranged as follows. In Section 2, the replacement and addition explosive breakdown point of the penalized logistic regression estimator are obtained respectively. Furthermore, we also show the replacement implosive breakdown point of the penalized MLE. Section 3 discusses a fast convergent iterative algorithm and Section 4 performs the simulation studies. Finally, Section 5 concludes. We introduce some necessary notations in this paper. Ifβ=(β1,…,βp)T∈pis ap-dimensional vector, thenL1norm ofβis defined as ‖β‖1=andL2norm ofβis defined as ‖β‖2= We start with a brief introduction of the logistic regression model. Denote byX=(Xij)1≤i≤p,1≤j≤n=(X1,…,Xn) the matrix of predictor variables, wherenis the number of observations andpthe number of variables. LetY=(Y1,…,Yn)Tbe the vector of responses, whereYiis either 0 or 1,i=1,…,n. The logistic regression model is given by (1) M-estimation of the parameters is often obtained by minimizing a certain loss function. While it is not suitable to use the quadratic loss for classification problems. Letγ=(γ1,…,γp+1)T=(α;β). Giving the observed sampleZ=(Z1,…,Zn), whereZi=(Xi;Yi),i=1,…,n. Specifically, Quadratic loss:l(γ,Zi)=(Yi-θi)2/2; Deviance loss: l(γ,Zi)=-2{Yilog(μi)+(1-Yi)log(1-μi)}; Exponential loss:l(γ,Zi)=exp{-(Yi-0.5)θi}. (1-Yi)log(1-μi)}. (2) Here, the regression estimator obtained by minimizing (2) is the MLE. For binary logistic regression model, there are three possible patterns of data points: complete separation, quasi-complete separation and overlap. Albert and Anderson[18]verified that the MLE of logistic regression models does not exist when the data types are completely separated or quasi-complete separated, while in overlap situation, MLE exists uniquely. Similar result was discussed in Ref. [19]. Thus, we concentrate on the overlap situation here. On the other hand, regularization methods generally consist loss functions and penalty terms. It is commonly used to obtain well-behaved solutions to over-parameterized estimation problems. Fan and Li[20]mentioned that a good penalty function could result in an estimator with unbiasedness, sparsity and continuity and asserted that bounded penalty functions can reduce bias and yield continuous solutions. Therefore, we try to add a penalty termPλ(β) to the loss function. Then the regression estimator is defined as (3) whereQ(γ,Z) is the objective function. Since the intercept term has no corresponding feature term and it is mainly used to fit the overall migration of the data, so it is not involved in regularization. L1penalty function, Pλ(|βj|)=λ|βj|. (4) L2penalty function, (5) SCAD penalty function, Pλ(|βj|)= (6) wherea>2 andλ>0 are the unknown parameters. To study the robustness of an estimator, Donoho and Huber[2]introduced two finite-sample versions of breakdown point, one is replacement breakdown point, the other is addition breakdown point. Generally speaking, the value is the smallest proportion of contamination that can lead the estimator’s Euclidean norm to infinity or to zero, which means the estimator becomes completely unreliable. Rousseeuw and Leroy[21]held that breakdown point can not exceed 50%. Intuitively, if more than half of the data are polluted, we will not be able to distinguish the original distribution from the pollution distribution. For penalized MLE in logistic models, we have the following theorem. ProofTheL1norm of a vectorβis denote as ‖β‖1, and the Euclidean norm as ‖β‖2. Since the two norms have topological equivalence, there exists a constantc≥1, such that ‖β‖1≥c‖β‖2. We replacemof the observations bymoutliers, then Considering the case ofγi=0,i=1,…,p+1, we haveμi=0.5,i=1,…,n. The objective function becomes We can see that the constantMonly depends onp. So either for the case ofn>por the situation ofn As mentioned above, there are two types of finite-sample breakdown point. Zuo[22]ever gave the quantitative relationship between replacement breakdown point and addition breakdown point of a large class of estimators whose breakdown points are independent of the configuration ofX. One may think that the influence of adding outliers may be different from that some of the raw observations are replaced by outliers. From the proof process of Theorem 1.1, it can be seen whether the arbitral observations are replaced or added, it does not matter. If we addedmoutliers to the raw data set, we could conclude the following theorem. The proof is similar to that of Theorem 1.1. Theorem 1.1 and Theorem 1.2 show that the penalized MLE is very robust in binary logistic regression models. Moreover, for multiple classification models, the theorems are also applicable. In logistic regression models with binary data, we verified that the explosive breakdown point of penalized MLE in logistic regression models gets the biggest value 0.5, which is a good result. (7) The following theorem shows that ‖β‖2tends to zero while 2pobservations of the raw sample are replaced by outliers. Theorem1.3In model (1), considering (3), the penalized MLE satisfies Case one:βjm>0, ≤-(M+N)‖β‖2+M‖β‖2 =-N‖β‖2<-Nδ=-τ. Thus Case two:βjm<0, >(M+N)‖β‖2-M‖β‖2 =N‖β‖2>Nδ=τ. Thus Theorem 1.3 implies that the number of contaminated data cannot exceed twice the number of independent variables, which shows the non-robustness of the estimator. The standard error of a regression estimator would not explode when the Euclidean norm of the estimator tends to zero. Therefore, this kind of breakdown is more difficult to detect. Croux et al.[12]proved that MLE of logistic regression model breaks down to zero when adding several outliers to the data set. Here, we discuss penalized MLE in replacement situation, and our result is not bad. In this section, we concentrate on the computation of (3). Approaches applicable to linear models may computationally infeasible to nonlinear regression analysis. In our model, the objective function is nonlinear, the general normal equation is a transcendental equation. we can only solve the problem by numerical methods in stead of algebraic methods. There are some fast algorithms for numerical computing. Efron et al.[23]introduced least angle regression. Balakrishnan and Madigan[24]presented the online algorithm and the MP algorithm for learningL1logistic regression models; Wu and Lange[25]used the coordinated descent (CD) algorithm to solve lasso regressions. Friedman et al.[26]derived the generalized CD algorithm for convex optimization problems. CD was also mentioned in Ref.[27], in which it was shown to gain computational superiority. It is proved that the block CD algorithm has linear convergence rate in Ref.[28]. Saha and Tewari[29]proved that the CD algorithm has the convergence rate ofO(1/p). Since this algorithm has many excellent properties, it is wise to use it in this paper. An approximate solution can be calculated by convergent iterative algorithms. we try to transform the deviance loss function into approximate squared loss function through Taylor expansion. In this way, the regression coefficient can be calculated more conveniently. Note that for multiple classification regression problems, the Taylor expansion for the ordinary objective function would become more complex. In these situations, one should consider the use of other numerical methods, such as Newton method, gradient ascent method, among others. If the loss function is deviance loss function, we would havel(γ,Zi)=-2{yilogμi+(1-yi)log(1-μi)}. Then for the logistic model and the probit model, we already have their distribution functions, it is easy to obtain their first order derivative function and two order derivative function. For logit model, we have And for probit model, we have Otherwise, if the loss function was exponential lossl(γ,Zi)=exp{-(yi-0.5)θi}, there is nothing to do withμi, so no matter how to constructui, we have l′θi=(yi-0.5)e-(yi-0.5)θi, According to the method of seeking extreme point, we set the first order derivative of the constrained objective function to all independent variables be zero. Then the parameters can be attained by solving the simultaneous equations. The first part of the objective function has been changed from Taylor expansion to square terms, and it is easy to find the derivative function of each order. Then consider penalty term. It is important to note that if we could not seek the first order guidance directly of the penalty term, such asL1penalty, we could apply the soft thresholding method introduced firstly by Donoho and Johnstone[30]. Then we apply CD algorithm. At thekthiteration, For the giving initialγ0, everyβj,j=1,…,phas the following explicit solution: ForL1penalization, (8) ForL2penalization, (9) (10) In practical application, the extreme point is usually the maximum or minimum extreme point we want. According to the fast convergence property of the CD method, we can easily obtain the convergent regression estimator. In this section, simulation studies on artificial data sets with different groups ofnandpare presented. We construct two data configurations, include the case ofn>pand the case ofn The first data configuration is withn=200 andp=5,n/2,n-20 respectively, which is corresponding to the low-dimensional data set. Assume thatXobeys the multivariate normal distribution,X~N(0,∑), where the covariance matrix ∑=(∑ij)1≤i,j≤pis assigned to ∑ij=0.5|i-j|, which implies the multiple multicollinearity between predictor variables. Using the coefficient vectorγwithα=0.2,β1=0.5,β2=-0.6,β3=1,β4=-0.8,β5=0.1, andβj=0 forj∈{1,2,…,p+1}{1,2,3,4,5}, the response variableYis generated according to model (1). Then, the second configuration represents the moderate case of high-dimensional.n=100 observations are generated and the value ofpisn+10, 2nor 4n. The independent variables are subjected to the distributionsN(0,∑) with ∑ij=0.1|i-j|. For regression parameters, we assume thatα=0.2, andβ1=-0.7,β1=1,β1=-0.3,β1=0.5,β1=-0.6, while other slope coefficientsβj=0.Yis also constructed according to model (1). Denote bykthe contaminated percentage,k=0, 25% or 50%. For each data set, we make different kinds of pollution. 1) No contamination; 2) Vertical outliers:kof the dependent variables in model (1) are changed, which means someYiwill become 1-Yi; 3) Leverage points: same as in (2), while for thekcontaminated observations, we drawing the predictor variables fromN(μ,∑) instead ofN(0,∑), whereμ=(20,…,20). There are several termination rules widely adopted in an iterative algorithm, such as the function descent criterion, the distance criterion, the gradient criterion. At present article, we use the distance criterion. For each cycle of the coordinate descent algorithm, the specific form of stopping criterion is (11) The maximum number of iterations is 1 000, and each regression coefficient should be of practical significance, likeγj<103forj=1,…,p+1. Given a parametric statistical model (sample space and sample distribution family), decision space and loss function, it is naturally desirable to specify a decision for each point in the sample space. We assume that the decision function is Yi=1 ifp(Yi=1|Xi)>0.5. (12) Here, 0.5 is chosen as the threshold as it is a common practice. In practical application, different thresholds may be selected for specific situations. If the accuracy of positive criteria was high, the threshold value could be larger. If we required higher positive recall, the threshold value should be selected smaller. We polluted the raw data in different degrees and different types of outliers. Following are the partial simulation results and all the above simulations are performed in Matlab2016b. Here, Fig.1 is one of the cross validation diagram. Fig.1 Cross validation result while n=200 and p=100 Table 1 and Table 2 express the results of logistic regression model whilen>pandn Table 1 Logistic regression results while there are vertical outliers Table 2 Logistic regression results with different numbers of leverage points Then, we change the link function to Probit link function. Table 3 shows the performance of probit regression, averaged over 500 simulation runs. Table 3 Probit regression results with different numbers of outliers Similarly, the MSE have a limit in Table 3, which means the regression estimator keeps bounded. In addition to some similarities between logistic and probit regression models, previous scholars found that the logistic regression coefficient is about 1.8 times bigger than that of the probit regression coefficient with the same data sets. Although the coefficients are different, the classification results are essentially similar. The meaning of the coefficient, the evaluation of the model and the hypothesis test are all similar. Furthermore, we find that the choice of the loss functions has an almost negligible effect on the prediction result. This might be the reason why less discussion about the impact on different loss functions was talked in classification models. This paper shows that penalized MLE has a high explosive breakdown point in binary logistic regression models. Accurately speaking, we can still get bounded regression coefficients even if the pollution rate of the observations reaches 50%. The property is shown by our simulation studies. In either logistic model or probit model, the regression estimators are robust in contaminated data sets. Also, we give the upper bound of implosive breakdown point of the slope parameter. Theorem 1.3 gives the upper bound of implosive breakdown point of slope parameter. However, for robust estimator, the bigger the breakdown point, the better. Naturally, we consider whether the implosive breakdown point has a larger lower bound by changing the penalty item or changing the loss function. For example, sparse LTS method is pretty robust in linear models, can we learn from the idea of trimming? As we know, SCAD penalty is a famous penalty term as it satisfies sparsity mathematical conditions. So it may lead to unexpected gains if we use this punishment. In our future research, we will pay more attention to it. While there is only a slight multi-collinearity between the explanatory variables, MLE is consistent, asymptotically valid, and asymptotically normal forn→+∞ under some weak assumptions. Fahrmeir and Kaufmann[31]did some research. With the increase of sample size, the standard error of parameter estimation will gradually decrease. After adding a penalty item, these properties may change. As for hypothesis test, we need more studies, not only on breakdown point, but also on the standard error.1 Main results

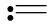
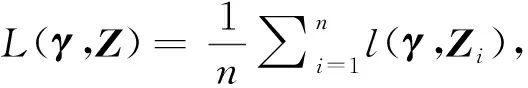
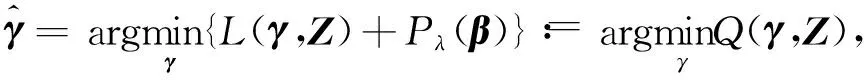
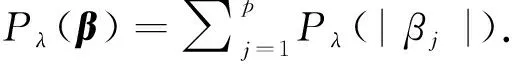
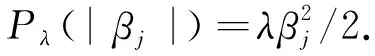
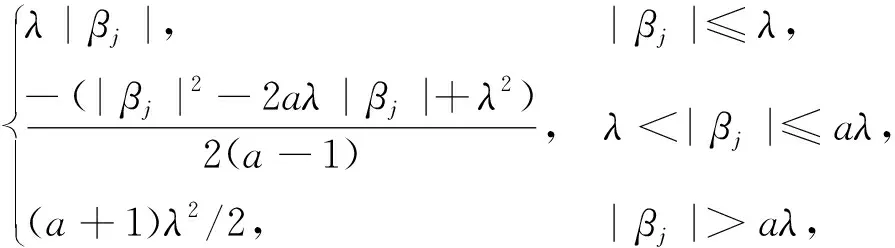
1.1 Explosive breakdown point
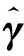
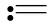
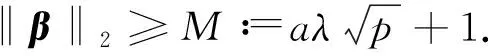
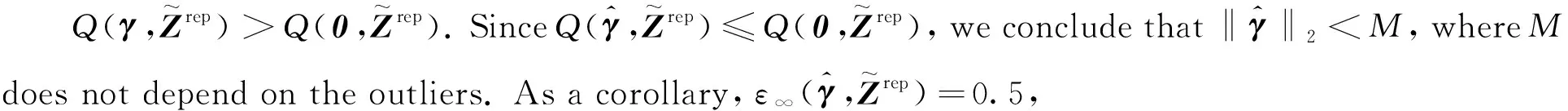
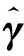
1.2 Implosive breakdown point
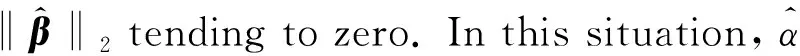
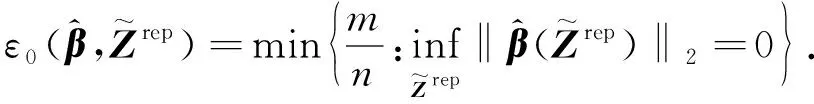
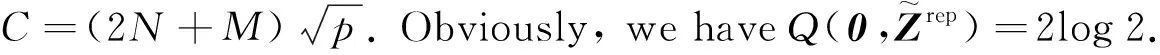
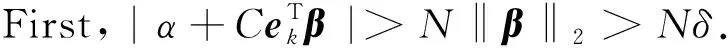
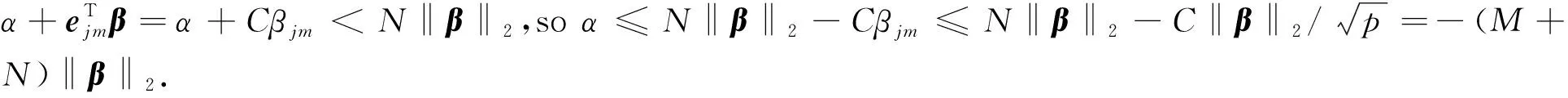

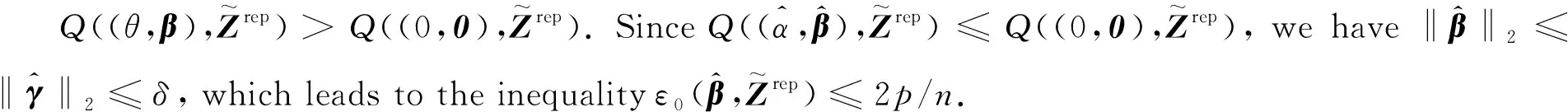
2 Algorithm
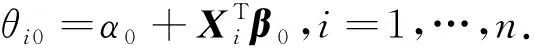

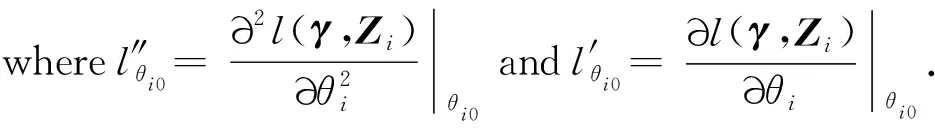
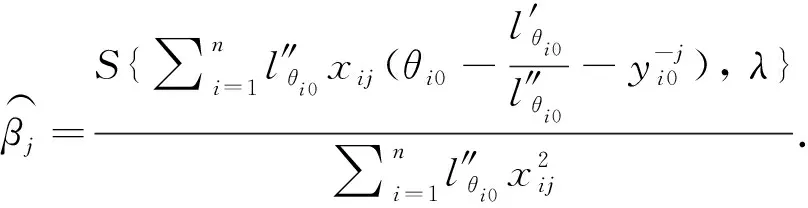
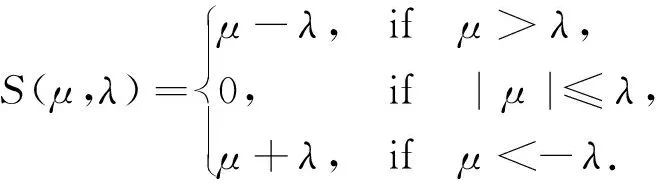
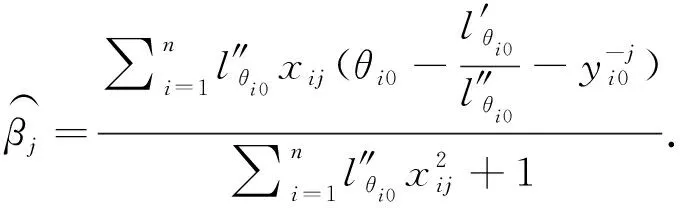
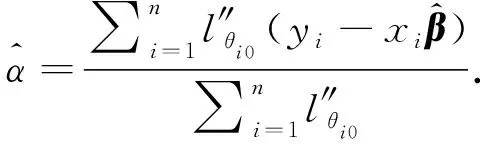
3 Simulation
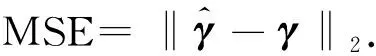
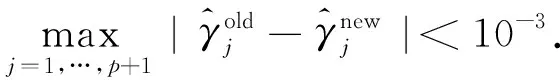
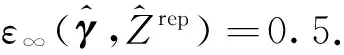

4 Discussion

