Logicality and the Logicism of Frege Arithmetic and Simple Type Theory*

Weijun Shi

Abstract.The logicism of Frege and Russell consists of two-fold components:the provability thesis and the definability thesis.It is safe to say that the provability thesis cannot be completely upheld.However,to justify or dismiss them,in particular,the definability thesis,one needs a criterion for logicality to determine whether the constants for the concept“the number of”and the membership relation,among others,are logical.The criteria that I shall adopt are logicality as isomorphism-invariance on the part of Tarski and Sher and logicality as homomorphism invariance on the part of Feferman.Tarski and Sher have pointed out that Russell’s constant for the membership relation is isomorphism-invariance on different occasions.I shall demonstrate the following conclusions in the article:First,this constant is also homomorphism invariance;Second,the constant for the concept “the number of” is neither isomorphism invariance nor homomorphism-invariance; Third,if logicality is isomorphism invariance or homomorphism invariance,then the definability thesis of Frege’s logicism(here Frege arithmetic)does not get justified; Forth,if logicality is isomorphism invariance,the thesis of Russell’s logicism (here simple type theory)is fully justified,whereas it is not so provided that logicality is homomorphism invariance.

1 Introduction

The logicism of Frege and Russell tries to reduce mathematics,i.e.,the fundamental axioms and theorems of number theory,to logic.But how should we make sense of such reduction? According to Carnap,the reduction consists of two theses([2],p.41):

?The concepts of mathematics can be derived from logical concepts by means of explicit definitions.

?The theorems of mathematics can be derived from logical truths by means of logical inferences.

Following Boolos,let us call the first thedefinability thesisand the second theprovability thesis.These two theses are independent:neither one is weaker or stronger than the other.The reason is that a logical truth can involve extra-logical concepts,while a truth involving only logical concepts may not be a logical truth.The examples are not far away to find.1‘?x?y(x y)’ does not contain extra-logical constants in the usual sense,but it is not a logical truth.‘?x(x= Russell ∨?(x Russell)’is a logical truth,even though it contains the extra-logical constant‘Russell’.It is not controversial that Frege subscribes to both theses.Unlike Frege,Russell,however,is committed himself to the definability thesis,but not to the provability thesis,because,as Boolos points out,he explicitly rejects the axiom of infinity as a logical truth inPrincipia Mathematica([4],pp.270–272).Which thesis Frege and Russell subscribe to is of historical significance.But it is of greater significance whether these two theses are on their own justifiable.

What is indispensable to the justification or rejection of the theses is a criterion for logicality and a notion of logical truth.In Frege’s or Russell’s system,according to the definability thesis,the definiens,in terms of which the constants of mathematics are defined,are logical in the sense that it involves only logical vocabulary thereof.According to the provability thesis,the axioms of these two systems are logical truths.Thus,logicism will stand and fall with different criteria for logicality and notions of logical truth.In this paper,we will make use of Tarski’s notion of logical truth,which is the standard one in logical textbooks.2Besides Tarski’s notion of logical truth,there are others,say,Quine’s substitutional conception of logical truth([17],ch.4).It is a precondition for this notion that the constant of languages is divided into logical and extra-logical ones.In other words,the criterion for logicality is a precondition for Tarski’s conception of logical truth.Let us see why it is so.

According to Tarski,any sentence?of a languageLis a logical truth if its sentential function??is true in all structures of the sentential function.The notion of logicality comes in when we transform a sentence into its sentential function.Suppose all constants(except variables)of the language have type symbols inT,which is defined as follows:

Definition 1

1.e ∈T;

2.Ifτ1,...,τn ∈T,then(τ1,...,τn)∈T.

Given a domainMof objects of typee,with each typeτ ∈Tis associated a setMτwhich is defined as follows:

Definition 2

1.Ifτ=e,thenMτ=M;

2.Ifτ=(τ1,...,τn),thenMτ=P(Mτ1×...×Mτn).

wherePis the subset operation in set theory.

LetMLbe the built-in domain of the languageL.Suppose the extra-logical constants occurring in?areE1,…,En,which are of typesτi(1 ?i?n),respectively.The sentential function??of?is obtained by substituting a variableXiof typeτifor each occurrence ofEiin?.?is a logical truth if??is true in all structures.3It is controversial whether Tarski takes all structures to share the same domain ML,i.e.,the built-in domain of the language L in[20].Bays argues that Tarski intends all structures to share the same domainML([1]),while others like Sher argues for the exactly opposite([18],p.41).Whether all structures share the same domain ML is of great significance to which sentence of the language is valid.Suppose the built-in domain ML of L has at least two objects.So the sentence‘?x?y(x y)’of L says that there are at least two objects in ML.Given that all constants in the sentence are logical,the sentence is a logical truth if all structures share the same domain ML.In contrast,if all structures do not necessarily share the same domain,then the sentence is not valid,because its sentential function,i.e.,itself,would be false in all structures whose domains contain only one object.It is not up to me to determine which reading is right here.I just take it that the domain can vary.For the point that the notion of logical truth is sensitive to logicality,which I want to emphasize,the controversy is not that much important.

Tarski’s notion of logical truth is sensitive to the notion of logicality,as Tarski himself comes to recognize.4According to Tarski,a sentence ? is the logical consequence of the sentences of the set R iff any model of the sentential functions of the sentences of R is also a model of the sentential function of ?.An extreme case of the notion of logical consequence is such that R is empty.In such case,we have the notion of logical truth.Now Tarski writes:The extreme would be the case in which we treated all terms of the language as logical:the concept of following formally5 would then coincide with the concept of following materially-the sentence X would follow from the sentences of the class R if and only if either the sentence X would be true or at least one sentence of the class R were false.([20],p.188)In order to see this sensitivity,let us look at an example.SupposeLcontains ‘Russell’,‘philosopher’,‘?’ and ‘=’ as its only primitive constants,and ‘Russell’ and ‘philosopher’ denote Betrand Russell and the propertybeing a philosopher,respectively.So the built-in domainMLofLcontains at least Russell,and the property is a subset of the domain which contains all philosophers.Consider the sentences:

5Here,by‘following formally’is meant what we call‘logical consequence’today.

(1) Russell is a philosopher.

(2)?x(x=x).

They are true in the structure with the domainML.Usually,‘Russell’ and‘philosopher’ are seen as extra-logical,while ‘?’ and ‘=’ are seen as logical.As a result,(1)is not seen as a logical truth,while(2)is seen as a logical truth,which accords with our usual or intuitive conception of logical truth.

(1)and(2)will be logical truths,if all of these primitive constants are logical.In this case,the sentential functions of(1)and(2)are themselves,because there are no extra-logical constants occurring in them that are to be substituted for by variables.Consequently,(1)and(2)are true in all structures with any domain.One might contest this by saying that (1) is false in the structure with the domain,say,{1,2},in which‘Russell’and‘philosopher’are interpreted as 1 and{2},respectively.This is,however,not true,because ‘Russell’ and ‘philosopher’ are logical,so that they are to denote Russell and the propertybeing a philosopher.So it is absolutely wrong to assign 1 and{2}to them,respectively.In other words,any structure with the domain{1,2}is just not a structure of the sentential functions of the languageLat all.

In contrast,if all of these primitive constants are extra-logical,then both(1)and(2) are not logical-truths.‘Russell’,‘philosopher’,‘?’ and ‘=’ are of typese,(e),((e)) and (e,e),respectively.Let ‘X1’,‘X2’,‘X3’ and ‘X4’ be variables of these types,respectively.So ‘X2(X1)’ can serve as the sentential function of (1),while‘X3x(xX4x)’ is the sentential function of (2).Then it is easy to find structures in which these two sentential functions are not satisfied.Consequently,(1)and(2)are not logical truths.

What distinguishes logical constants from extra-logical ones is that the former are to be interpreted uniquely or in the same way on all structures,while the latter do not have to be so.In Tarski’s original formulation of the concept of logical truth,it is required that each sentence be transformed into its sentential function.This requirement,however,is not necessary.For to assess the validity of a sentence,we can interpret all of its logical constants as their default denotations or meanings on all structures,and all of its extra-logical constants arbitrarily with their types being respected;there is no need to replace those extra-logical constants by variables of the same types,and then assign objects of the same types to these variables.For example,given that‘?’is logical,it is to be interpreted as{A:on each structure with any domainM,in order to determine whether(say)‘?x(x=x)’is valid.It cannot be assigned other denotations,say,{M}.Similarly,if‘Russell’is logical,it is to be interpreted as the person Betrand Russell on each structure.(In this connection,Russell must be in the domain of the structure.) If a constant is extra-logical,then besides its default denotation,it can be interpreted as any objects of the same type.E.g.if‘?’is extra-logical,then it can be interpreted as objects of the type((e)),say,{A:A ?M}and{M},on any structure with a domainM.By the same token,if ‘Russell’ is extra-logical,then it can be interpreted as any object of typeeon all structures,even if Russell is not in their domains.6When I write these three paragraphs,I fully keep in mind Sher’s interpretation of what distinguishes extra-logical constants from logical ones,which does not accord with my reading.Sher writes:It has been said that to be a logical constant in a Tarskian logic is to have the same interpretation in all models.Thus for “red” to be a logical constant in logic L,it has to have a constant interpretation in all the models for L.I think this characterisation is faulty because it is vague.([18],p.45)I do not hold that from the perspective of Tarski,a logical constant such as‘?’should have the same interpretation in all models.Clearly,given any two nonidentical domains(sets),the interpretations of this quantifier cannot be the same in the set-theoretical sense.Rather,I hold that logical constants should be interpreted uniquely or in the same way.What the words‘uniquely’or‘in the same way’means is already glossed by taking the example of‘?’as logical in the paragraph.Now Sher asks how one can interpret‘red’(assume that the predicate denotes the set of all red objects)in the same way in all models if it is a logical constant.My answer is that if ‘red’ is to be counted as logical,then a model whose domain does not contain all red objects just fails to qualify as a model of the logical language in which‘red’is identified as logical.In the case,not all sets can serve as the domain of models of the language.For Sher’s point of view on the question of the roles of logical constants,see[18,pp.46–52].

2 Frege’s logicism

Frege’s original system in [11],via.second-order logic plus the axiom V,is inconsistent; but the system can be rendered as consistent in different ways.For example,predicative second-order logic plus the axiom V is consistent([13]).But it is too weak to derive Peano arithmetic(PA)7PA has five axioms:PA.1 Zero is a natural number.PA.2 If x is a natural number,its successor is a natural number.PA.3 If x is a natural number,its successor is not zero.PA.4 If x and y are natural numbers and their successors are equal,then x is y.PA.5 Induction axiom.as its theorems([13])8In the paper,Heck shows that the induction axiom is not provable from the system.But what is known as Robinson arithmetic is interpretable in the system..In this paper,I will not consider the system for two reasons.The first is its weakness;the second is that from the perspective of ZFC,which we are going to make use of as the metatheory,the axiom V is just false.Instead,I will consider another version of Frege’s original system,Frege arithmetic(FA),which is consistent and strong enough for PA ([4],pp.183–201).

The language of FA is a second-order language,which contains the following as its primitive vocabulary:

(i.1) Variables:variables for concepts and relations and objects.

(i.2) Constants:first and second-order quantifiers,propositional connectives,identity.

(i.3) Constants:?.

Terms,formulas and sentences are defined in a canonical way.‘?’ is a functional constant of type((e),e),which is informally read as‘The number of’.Syntactically,attaching a variable‘F’for concepts to‘?’forms the term‘?F’for objects.

Besides all axioms of second-order logic,FA has two more axioms:

(HP)?F?G(?F=?G ?F eq G).9Here‘F eq G’is an abbreviation of a second-order formula which says that the concepts F and G are equinumerous.

(3)?F?!x(x=?F).

What(HP)expresses is that the numbers of two concepts are equal iff the concepts are equinumerous.(3)says that every concept has a unique number.

Just as the first-order PA has a standard interpretation or standard model([16],p.160),FA also has its standard interpretation.The denotation of the constant‘?’in the standard interpretation is its default denotation.Give a domainM,the domains of object variables,concept variables and binary relation variables areM,P(M),andP(M ×M),respectively.The constants of(i.2)are interpreted in the canonical way given that they are logical.As for‘?’,its denotation is a function fromP(M)toM.But what function is the default denotation of the constant?

For Frege,(HP) is true,if not a logical principle.Frege sees the axiom V as‘a(chǎn) fundamental law of logic’([10],p.142)and derives(HP)as a theorem of it(plus necessary definitions)in second-order logic.Hence Frege takes(HP)to be true.(Admittedly,the axiom V is inconsistent in second-order logic.But what concerns us here is not the problem of consistency,but whether or not Frege thinks of (HP) as true.) Therefore,the default denotation of ‘?’ is such a function that renders (HP)true.There is no such function in any structure with a finite domain ([4],pp.213–214,pp.305–306),because if there aren(any finite number)objects in the domain,there will ben+1 equinumerous concepts.Hence its default denotation is any functionf:P(M)→Mthat satisfies the condition:

(C) For anyF,G ∈P(M),iff(F)=f(G)iff|F|=|G|.10|F|is the cardinality of the set F.

Mis infinite.

To assess if Frege’s logicism succeeds,it is necessary to determine the logicality of the constant‘?’with its default interpretationf,as well as of the constants in(i.2).Boolos holds that:

(A) The constants in(i.2)are logical.11Boolos does not explicitly hold(A).But(A)is usually taken for granted.

(B) The constant‘?’is extra-logical([4],fn.3,p.186).12Here Boolos explicitly says that he sees the constant as extra-logical,while Frege sees it as logical.

To survey whether(HP)is a logical truth,‘?’is to be assigned any function of type((e),e)in the structure with any domain,thanks to(B).(HP)is false in the structure with the domainM,either finite or infinite,in which ‘?’ is assigned the functiongthat for anyA,B ∈P(M),g(A)=g(B).Therefore,(HP) is not a logical truth.Besides,the rest axioms of FA except(HP)are logical truths.

Boolos’s assessment of Frege’s logicism is,therefore,as follows:

Premise(A)and(B)hold.

ConclusionThe definability thesis and the provability thesis of Frege’s logicism are not justified.

The reason that the provability thesis is not justified is that(HP)is not a logical truth.13(PA.1),(PA.2) and (PA.5) are theorems of second-order logic (with additional definitions) plus(3).The derivation of(PA.3)and(PA.4),which requires the existence of infinite objects,needs(HP).Consequently,(PA.1),(PA.2)and(PA.5)are logical truths,while(PA.3)and(PA.4)are not.But why is the definability thesis is said to be unjustifiable? It seems that Carnap and Boolos both subscribe to such an inference:If the definition of any arithmetical constant involves extra-logical constants,then the former is extra-logical; since the constant‘?’is extra-logical,so is any arithmetical constant whose definition involves it.But the claim(+)that if the definition of any arithmetical constant involves extralogical constants,then the former is extra-logical is not guaranteed at all.Whether the claim holds up depends upon what it is for a constant to be logical.As will be seen later,although all constants in the language of Russell’s simple type theory are logical in the sense that all of them are homomorphism-invariance,almost all arithmetical constants for numbers are not homomorphism-invariance.

Before introducing Russell’s system,let us pause for a while to look at Carnap’s assessment of the definability thesis.Carnap,as opposed to Boolos,thinks that the definability thesis is fully justified.Carnap says that Frege and Russell arrive at the same conclusion about the logical status of natural numbers independently:natural numbers are‘logical attributes which belong,not to things,but to concepts.([2],p.42)To be precise,to say that the number of a conceptFisnjust means that there are exactly n objects which fall underF.‘The number of the conceptF’is repressed by Carnap as‘nm(F)’.According to Carnap,‘nm(F)’is defined as:

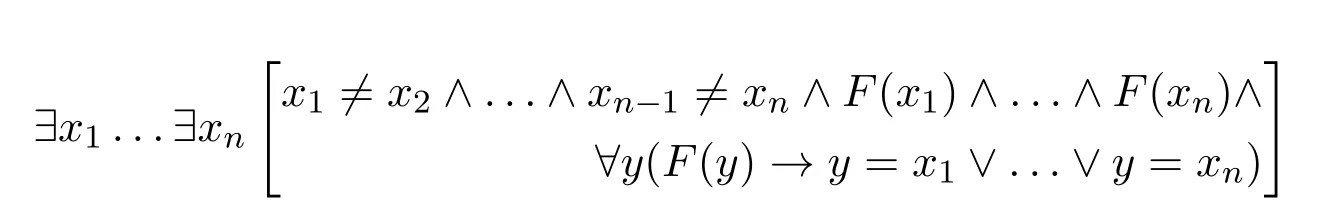
Carnap regards all familiar logical constants of first-order logic as logical,without saying anything on second-order quantifiers.([2],p.42)(Of course,Carnap owes us a criterion for logicality.) Since the definiens is a formula of first-order logic,Carnap asserts that the notion‘the number of the conceptF’is logical.In addition,he holds that other arithmetical concepts such as addition and natural numbers also can be defined by formulae which involve only logical vocabulary.But I think that Carnap’s assertions are not justified for two reasons.

First,the aforementioned definiens involves not only constants which Carnap sees as logical but also the constant‘F’,which is a constant rather than a variable.The constant is not on Carnap’s list of logical terms and is usually seen as extra-logical.Second,Carnap asserts that other arithmetical concepts are definable in terms of the logical terms of first-order logic.But it is hardly clear how this can be done.14Hodges([14])forcefully argues that the arithmetic truths,say,(4) 7+5=12.(5) The successor of 1 equals to 2.express the same thought(Gedanken)as(6) ?X?Y[?7xFx ∧?5xGx ∧??x(Fx ∧Gx)→?12x(Fx ∨Gx)].(7) ?F(?1xFx ∧?y?Fy →?G?2xGx).(Hodges says clearly that (4) expresses the same thought as (6).That (5) expresses the same thought as(7)is not mentioned by Hodges.But it is clear that this assertion is made in the spirit of Hodges.)(6)and(7)are sentences of second-order logic.So no appeal can be made to these examples to back up Carnap’s assertion that all arithmetical concepts can be defined in terms of formulae of first-order logic.Takethe concept‘natural numbers’as an example.Taking into consideration that Carnap has defined ‘0m(F)’,‘1m(F)’ and so on,one might suggest defining the concept as‘x=0m(F)∨...∨nm(F)∨...’.However,the definiens is not a sentence of first-order logic,because it contains infinitely many disjuncts.

3 Russell’s logicism

Simple type theory (STT),which is a simplification of the ramified system inPrincipia Mathematica,is consistent.Moreover,it is so strong that not only PA but also set theory can be devolved out of it.STT is a higher-order system.For deriving PA,STT can be seen as a forth-order system.The language of STT contains the following vocabulary:

(ii.1) Variables‘xn’(0 ?n?3)for objects of typen.

(ii.2) First-order quantifiers (‘?x0’),second-order quantifiers (‘?x1’),third-order quantifiers(‘?x2’),forth-order universal quantifiers(‘?x3’)and propositional connectives.

(ii.3) The constant‘?’(for membership).

The atomic formula of the language is of the form ‘xn?xn+1’ (informally,xnis a member of the setxn+1).

STT has three axioms,i.e.,the axiom of extension and the axiom of comprehension and the axiom of infinity([16],pp.290–291):

(Inf)??x3[02?x3∧?x2(x2?x3→sx2∈x3)→?2?x3].15The original formulation of the axiom of infinity in[16,pp.290–291]is not(Inf).But it is equivalent to(Inf).(Inf)contains three constants‘0’(zero of type 2),‘s’(successor)and‘?2’(empty set of type 2).The occurrence of these constants can be eliminated from(Inf)by means of the definitions of them as follows:1. xn??n+1 iff xn xn.2. x2=02 iff x2={?1}.3. s(x2)iff{y1 :?z0[z0?y1 ∧y1{z0}?x2}].For more details,see[16,pp.290–293].

(Inf)says that?2,the empty set of type 2,is not a number,which is equivalent to say that there are infinitely many objects of type 0.

STT has its standard interpretations.SupposeM0=Mis the domain(any nonempty set) of a structure.LetMn+1=P(Mn).Then each variable ‘xn’ ranges over the setMn.Since the constant ‘?’ is of type (n,n+1),its denotation must be some relation that is a subset ofMn×Mn+1.The standard or default denotation of the constant is the relationR={(a,b) :a ∈Mn,b ∈Mn+1,a ∈b}.Among all relationsRis the relation{(a,b) :a ∈Mn,b ∈Mn+1,a ∈b,Mis infinite},which should be the default interpretation of the constant‘?’if Russell sees(Inf)as a truth.However,Russell sees(Inf)only as‘a(chǎn)n arithmetical hypothesis’([4],p.268),so that he does not assert that it is a truth,let alone a logical truth.So the default denotation of the constant is anyR.

In the same vein,to assess whether the definability thesis and the provability thesis of Russell’s logicism succeed,we have to determine the logicality of the constants in(ii.2)and(ii.3).In this connection,it is generally held that:

(A*) The constants in(ii.2)are logical.

(B*) The constant‘?’is logical.

Now it might be problematic to say that ‘?’ is generally seen as extra-logical.For in logical books,say,[12,ch.4]and[16,pp.289–293]in which the theory of types is discussed in detail,the authors do not explicitly mention whether this constant is logical.But I suggest that it is at least seen as logical by some authors.For example,Boolos remarks that‘one who accepts the theory of types will almost surely regard Infin ax16By Infix ax is meant the axiom of infinity.as true and in logical vocabulary’.([4],p.271) Another case that can be made for(B*)has something to do with the interpretation of the constant on structures.According to Hatcher,the constant is assigned the relationR={(a,b):a ∈Mn,b ∈Mn+1,a ∈b}on each structure with the domainM.This indicates that Hatcher sees it as logical,otherwise it should be interpreted as any relation of type((e),e).

Because of(A*)and(B*),the constants in(ii.2)are interpreted on each structure in a canonical way,and‘?’is interpreted asR={(a,b):a ∈Mn,b ∈Mn+1,a ∈b}on each structure.As a result,it is easy to show that the axioms of STT except(Inf)are logical truths.(Inf)is not a logical truth,because it is false in any structure with a finite domainM.

Concerning Russell’s logicism,it is generally held that

(Premise*)(A*)and(B*)hold.

(Conclusion*)The provability thesis of Russell’s logicism is not justified,while the definability thesis thereof is justified.

The first part of(Conclusion*)holds,because(Inf)is not a logical truth.17All axioms of PA except(PA.4)are theorems of the axioms of extension and comprehension.So the former is logical truths.The derivation of(PA.4)from STT needs(Inf).Since(Inf)is not a logical truth,so is(PA.4).When it comes to the second part of(Conclusion*),the claim(+)on p.68 is taken for granted.As is already pointed out,whether the claim holds is completely determined by the conception of logicality.Anyone who wants to defend(Conclusion*)and(Conclusion)has to offer a criterion for logicality which can justify(Premise*)and(Premise).Now I will turn to such criterion next.

4 Logicality as invariance under morphisms

There are different approaches to logicality.Among them is Tarski’s approach,according to which logicality is to be characterised as invariance under isomorphisms.This approach has the advantage of mathematical precision.For this reason,I will look at if it can be invoked to justify(Premise)and(Premise*).

The motivation underlying Tarski’s approach is that logical notions are formal in the sense that they do not distinguish objects,i.e.,they are insensitive to the switching of objects.SupposeMis a set of objects of typee.letfbe any bijection onM.Then,for any objectOof typeτ ∈T,Ois mapped underfto another objectf(O).Tarski suggests thatOis a logical object if it is invariant under any transformationf,i.e.,O=f(O)([22]).A constant is logical if its reference is a logical object in Tarski’s sense.However,unlike Tarski,logicians and philosophers after him tend to speak of logicality of operations across domains,rather logicality of objects on a single domain.But these two different modes of dealing with logicality are more or less the same in their spirits.I will follow the mainstream in the paper.

There are three variants of the approach at issue:Tarski and Sher take logicality to be isomorphism-invariance; Feferman takes it to be homomorphism-invariance;Bonnay takes it to be potential isomorphism-invariance.For any constant whose type level18The level of types are defined as follows. level(e)=0.For any type τ=(τ1,...,τn) ∈T,level(τ)=max(level(τ1),...,level(τn))+1.is ?2,all of these variants fit for deciding their logicality.But for any constant whose type level is larger than 2,the third variant is not applicable without being generalised.The reason is related directly to the definition of potential isomorphisms,as is to be explained as follows.For this reason,I shall not consider the third variant,because some constants of the language of STT and FA have type levels larger than 2.

To formulate the content of the first two variants,we need the definitions of the concepts ‘the denotation (or operator) of a constant associated with each domain’,‘a(chǎn)rgument-structures’,‘isomorphisms’and‘homomorphisms’.These definitions,or more exactly,the ways of formulating these definitions,which I will make use of below,are due to Sher.

Given a domainM(infinite on some occasion),each constantCof typeτhas a unique denotationfC(M)onM,which is a member of the setMτ.19Sher requires that each constant should have a unique denotation on every domain.As a result,the predicate‘red’is to have a denotation on a domain containing no red objects at all.I just require that it have a denotation on a domain containing all red objects(and possibly others).So the any isomorphic(or homomorphic) structures in (Tarski–Sher Thesis) and (Feferman Thesis) below are just such that their domains contain the default denotation of the constant C.I deviate from Sher’s way of assigning objects to constants.By a domainMis always meant a non-empty set of objects of typee.For simplicity,we say thatfCis the denotation ofConM.If the constantCis of typeτ,we also say that its denotationfC(M)is of typeτ.Let us give some examples.

?fRussell(M)=Russell,ifRussell ∈M.

?f=(M)={(a,b):a ∈M,b ∈M,a=b}.

?f?(M)={M}.20The first-order universal and existential quantifiers are of type((e)).

?f?(M)={A:A ?M,A?}.

?(M)={A:A ?P(Mk).21This kind of identification of k-ary second-order existential quantifier is due to J.Kontinen([15]).Originally,given a domain M,J.Kontinen identifies the denotation of as the set{(M,A) :A ?P(M),A ?}.In order to keep the uniformity,we change Kontinen’s original way of identifying the denotation of constants into the current one.Such change is not essential,though.Kontinen says that ‘the first example is the familiar k-ary second-order existential quantifiers.’ This remarks shows that with respect to second-order quantifiers,we should not speak of their denotations generally;rather we should speak of the denotation of a second-order quantifier binding a variable for k-aries relations.The reason is that in(say)‘?x’x denotes any object of type e,while in the second-order quantification‘?X’X denotes any k-ary relations of type(e,...,e)with k e’s.

?(M)={P(Mk)}.22Here I follow Kontinen in his spirit in identifying the second-order universal quantifier in the framework of relational types.

?f?(M)=f,wherefsatisfies the condition:

(C)For anyA,B ∈P(M)anda,b ∈M,if(A,a)∈f?∧(B,b)∈f?,then|A|=|B|if and only ifa=b.

?f?(M)={(a,b):a ∈Mτ,b ∈M(τ),a ∈b},whereτ=(...(e)...)(npairs of parenthesis,n?0).23The type symbol n is equivalent to(...(e)...)in the system of relational type symbols.

Given any setM(maybe infinite on some occasions),with each vocabularyCof typeτ=(τ1,...,τn)is associated an+1-tuples1...an,where eachaiis of typeτiand therefore is an element of the set.Eachaiis thei-th argument of the denotationfC(M)ofConM.Following Sher,let us call the tuple1...anthe argument-structure of the constant C on M.For example:

? The argument-structure of ‘Russell’ is,where Russell is a member ofManda ∈M.

? The argument-structure of‘=’is,wherea,b ∈M.

? The argument-structure of‘?’is,whereA ∈P(M).

? The argument-structure of‘?’is,whereA ∈P(M),a ∈MandMis infinite.

? The argument-structure of‘?’is,wherea ∈MτandA ∈M(τ).

With the notion‘a(chǎn)rgument-structures’at our disposal,we can define the concepts of isomorphic-and homomorphic argument-structures.SupposeMandNare two universes andfis a bijection fromMtoN.Then,the bijection will induce a bijection from the setMτto the setNτfor any typeτ=(τ0,...,τn).

Definition 3

1.Ifτ=e,thenfτ=f.

2.Ifτe,thenfτ(A)=:(a0,...,an)∈A)},whereA ∈Mτ.

Definition 4Any two argument-structures,whereaiandbiare of the same typeτ=(τ0,...,τn),are isomorphic,if and only if:

1.m=n;

2.There is a bijectionffromMtoN;

3.For each 1 ?i?m,fτ(ai)=bi,wherefτis defined in Definition 3.

We can drop the subscript for types,writingf(A)instead offτ(A),because the type of A makes it clear which function is at issue.24For example,suppose that M= {1,2},N= {a,b}and f(1)= a,f(2)= b.Then,each set of type(e),say,the set{1,2},will be mapped to the set{a,b}.Each set of type((e)),say,the set{{1}},will be mapped to the set{{a}},etc.SupposeMandNare two universes andfis a surjection fromMtoN.Then,the bijection will also induce a surjection from the setMτto the setNτfor any typeτ=(τ0,...,τn).

Definition 5

1.Ifτ=e,thenfτ=f.

2.Ifτe,then the domain offτ,in notation,Dom(fτ),is defined as follows:

?Dom(fτ)={A ?×...×:?a1,b1∈...?an,bn ∈?(a1,...,an)∈A ?(b1,...,bn)∈A]}.

?fτ(A)=.25By‘?’and‘?’are meant‘if,then’and‘if and only if’.

Often we do not care what the induced function onMτwith a very complex typeτis.Rather,what concerns us is simple types.For example,for the type (e,...,e),f(e,...,e)is defined as follows：

f(e)(A)={(f(a1),...,f(an)) :(a1,...,an)∈A},and its domain is{A ?M:?ai,bi ∈M,f(ai)=f(bi)?(a1,...,an)∈A ?(b1,...,bn)∈A}.

Definition 6Any two structures1,...,amand1,...,bn,whereaiandbiare of the same typeτ=(τ0,...,τn),are homomorphic,if and only if:

1.m=n;

2.There is a surjectionffromMtoN.

3.For each 1 ≤i≤m,fτ(ai)=bi,wherefτis defined in Definition 5.

Definition 6 is very different from Sher’s formulation of homomorphic argumentstructures in [19,p.334].The difference lies in that the induced function that Sher makes use of in her formulation is not the one defined in Definition 5.Rather,it is the one that results from Definition 3 by replacing the bijectionftherein with a surjection.I shall refer to this resultant definition as‘Definition*’later.Definition*is not loyal to Feferman’s concept of homomorphism-invariance which is defined by using functional types([8]).26The concept of homomorphism invariance can be specified in terms of relational types or functional types.For more on the relation between these two methods of specifying the concept,see[5,p.18,p.21].

SupposeMandNare any two domains,Cis a constant of typeτ=(τ1,...,τn),and the denotations ofConMandNarefC(M) andfC(N),respectively.M=1,...,amandN=1,...,bnare the argument-structures ofConMandN,respectively.According to Tarski and Sher([18,19,22]),Cis a logical constant iffCis invariant under isomorphisms.To be precise,

It is worthy of mentioning that Sher imposes such a restriction on the constantC([18],p.54) that its level is ≤2.We will not respect the restriction,because some of the constants of the language of FA and STT have levels larger than 2.

Feferman rejects the thesis,because,among others,it overgeneralises the domain of logical notions by admitting many mathematical and set-theoretical notions such as alephs.In order to narrow the expanded field,Feferman uses homomorphisminvariance to characterize logicality([7,8,9]):

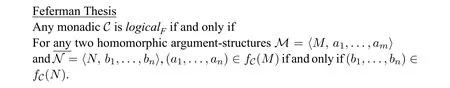
Compared with (Tarski–Sher Thesis),Feferman’s thesis narrows the field of logic notions dramatically.For example,all cardinal quantifiers‘?n’,eithern < ?0orn≥?0,fail to pass the test of the thesis.In addition,the constant for identity,which is usually seen as a logical vocabulary,is also excluded by the thesis from the field of logic.Having said that,there are still certain constants for set-theoretical notions,say,‘being a well-ordering’and‘being well-founded’,that survive the thesis.

Faced with these two shortcomings of(Feferman Thesis),i.e.,the exclusion of identity and the inclusion of the aforementioned set-theoretical notions,Feferman turns to Quine’s way of handling identity in a language with standard grammar([17],ch.5) and the notion of polyadic quantifiers,respectively.Bonnay,while agreeing with Feferman that (Tarksi-Sher thesis) overgeneralises logic,rejects the expedient of appealing to the notion of polyadic quantifiers.Bonnay suggests characterizing logicality in terms of potential isomorphism-invariance ([3]).However,Bonnay’s approach is only applicable to constants whose type level is ≤2,because in his definition of the concept‘partial isomorphism’27See[6,pp.181–183].between two structures1,...,amand1,...,bn,eachaiandbiare at most of level 1.As is already pointed out,the concept of potential isomorphism-invariance can be generalised to any constant with any type.But I will not do the generalisation here;rather I will focus on the two theses mentioned above.

Now let me turn to set up a criterion of logicality for propositional connectives,which denote truth-functions.SupposeSis a propositional connective andGSis the truth-function it denotes.According to Sher and Feferman,Sis logical,ifGSis permutation-invariant on the domain{T,F}.To be precise,

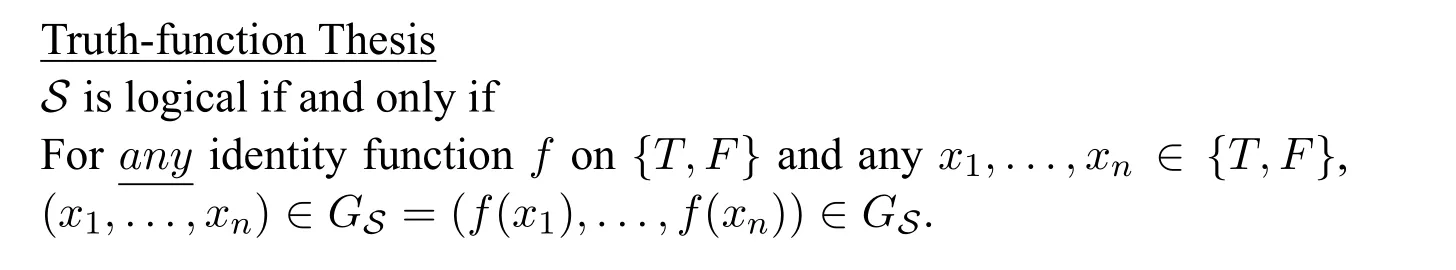
For constants with relational types,the thesis on logicality is that logicality is invariance under isomorphisms or homomorphisms.For propositional connectives,the thesis on logicality is that logicality is permutation-invariance.One might be wondering if there is any connection between these two theses.In other words,what is motivation for choosing the identity function rather than others in the latter thesis? There is,in fact,a nice connection.28There are different accounts for the connection,see[22,fn.6];[19];[3,p.11].For any vocabulary C of the type(τ1,...,τn)in T,its denotation on domain M is the n-ary relation RM(α1,...,αn) ? × ...× ,where each n-th argument is a member of the set .Now following Bonnay,let us identify the denotation of C as the class of structures fC= {M,α1,...,αn :(α1,...,αn) ∈RMand M is any domain}. C is logicalTS( logicalF),if for any two isomorphic (or homomorphic) argument-structures M,a1,...,an and N,b1,...,bn, M,a1,...,an ∈fC if and only ifN,b1,...,bn ∈fC.Let the True and the False be the sets ?and{?},respectively.The propositional connective,say,‘?’,has as its denotation the class f?= {M,?,{?},M,{?},? :M is any domain}.This can be done for all propositional connectives.For any two argument-structuresM,a1,...,anandM,b1,...,bn,where each ai and bi is the True or the False,whatever function g : M →N is,it is always the case that f(ai)= bi.So truth-values are not switched.Consequently,all propositional connectives are logicalTS and logicalF.Thanks to the connection,I do not distinguish betweenlogicalityTSandlogicalityFconcerning propositional connectives.It stands to reason that all propositional connectives in (i.2) and (ii.2) are bothlogicalTSandlogicalF.

5 Logicality of quantifiers

It can be easily shown that all quantifiers in(i.2)and(ii.2)arelogicalTS.Now let us have a look at whether they arelogicalF.Take universal quantifiers‘?’and‘’as an example.

‘?’ is not homomorphism-invariant according to Definition*.The argumentstructure of ‘?’ on any domainMis,whereA ?M(Ais of type (e)).Consider the argument-structuresand,whereM={1,2,3},N={4,5},A={1,2},B={4,5},andg:M →Nis such thatg(1)=4,g(2)=g(3)=5.andare,then,homomorphic,becausegis a surjection andg(A)=B.It is not hard to see that‘?’is not invariance underand,because{1,2}f?(M),i.e.,{1,2}M,but obviously,{4,5} ∈f?(N),i.e.,{4,5}=N.However,Sher writes:

(a) isomorphism-invariant operators that are also homomorphism-invariant.

(ii) The existential and universal quantifiers.([19],p.335)

If Sher makes use of Definition*,she has to admit that ‘?’ is not homomorphism invariance.

As is said,Sher’s Definition*does not accord with Feferman’s own.It can be proven easily that by Definition 6,‘?’islogicalF.The structuresandmentioned above,which are homomorphic in the sense of Definition*,are not homomorphic any more.For the functiong(e)is not defined for the setA={1,2},that is,it is not a member of the domain of the function.This is so,becauseg(2)=g(3)=5,but 2∈Aand 3A.

We have to decide whether or not the higher-order universal quantifiers in(i.2)and(ii.2)arelogicalF.As Feferman proves in the example 3 of[8],the second-order universal quantifier‘’is notlogicalF29Feferman only proves the special case in which k=1.According to Feferman,the operation associated with the quantifier ‘’ on a domain M is the function of type ((e →b) →b) →b such that (f)=[T,if ?p ∈Me→bf(p)=T,else F],where f is of type(e →b).Feferman works with functional type symbols.With relational type symbols,‘’is of type(((e))),and the operation associated with it on a domain M is,correspondingly,the set{P(M)}..Let us give another,simple proof within the framework of relational type symbols.LetM={1,2,3}andN={4,5},andg:M →Nsuch thatg(3)=5,g(1)=g(2)=4.Considerand,which are two argument-structures of‘’,whereA={{1,2,3},{1,2},{3},?}andB={{4,5},{4},{5},?}.Each member ofAandBare of type (e).andare homomorphic underg.30To see this,we have to show that A is in the domain of the function g((e)).The domain of g(e) is{X ?M :?x,y ∈M[g(x)=g(y)?x ∈X ?y ∈X]}.Therefore,domain of the function g((e))is{Y ?P(M) : ?x,y ∈Dom(ge)[ge(x)= ge(y) ?x ∈Y ?y ∈Y]}.Now it is easy to verify that A ∈Dom(g((e))).Similarly,it is easy to show that each member of A is in the domain of g(e).Moreover,g((e))(A)=B.However,A(M),becauseAP(M),whileB ∈(N),becauseB=P(N).

What is the implication of the fact that the quantifier‘’is notlogicalF? Feferman writes:

In any case,I count it as an argument in favor of the homomorphism invariance condition for logicality that it excludes second-order,and thence higher-order,quantification,by example 3 of the preceding section.([8])

Feferman would be definitely right if he says that the second-order universal quantifier,as well as universal quantifiers of even much higher-order,is notlogicalF.But he says‘it excludes second-order,and thence higher-order’.I cannot see how(Feferman Thesis)can exclude the second-order existential quantifier‘’.Its denotation on any non-empty domainMis(M)={A:A ?P(Mk),A?}.Given any two homomorphic argument-structuresand,whereAandBare of type ((e),...,(e)) (koccurrences of (e)),it cannot hold thatA ∈(M) andB(N).Similarly,it is also impossible thatA(M)andB ∈(N).For no surjection can map a non-empty set(an empty set)onto an empty set(a non-empty set).

It seems abnormal that the second-order quantifier ‘’ is notlogicalF,while the second-order ‘’ is so,because they are usually definable one another.31One should not be concerned with this abnormality too much,because there is a version of invariance under homomorphism which even bans operations definable in terms of first-order logical operations from being logical,see[5].E.g.,‘X’ is defined as‘X?’.Intuitively,given that ‘?’ and ‘’ arelogicalF,so would be ‘’.But as is already shown,is notlogicalF.So the intuition might be unreliable.The first-order universal and existential quantifiers are bothlogicalF.This seems to verdict the observation that if we take one of them to be a primitive logical constant and define the other in a canonical way,then the defined one would also qualify as logical.This observation is proved by Feferman’s theorem 6 in[8],according to which,any operation definable from the operations of first-order logic without identity is also definable from monodic homomorphism-invariant operations in terms of negation,conjunction and first-order existential quantifier,and vice versa.This theorem has nothing to do second-order quantifiers,however.So the aforementioned intuition does not get supported by it.

6 Logicality of the constants for the concept“The number of”and the membership relation

Let us look at if the constant in(i.3),i.e.,‘?’,and the constant in(ii.3),i.e.,‘?’,arelogicalTSandlogicalF.If a constant is notlogicalTS,then it is notlogicalF,because any homomorphism invariance is isomorphism invariance.I will show that‘?’is notlogicalTS.For this purpose,it suffices to find two isomorphic argument-structuresand,whereA ∈P(M),a ∈M,B ∈P(N),b ∈N,such that it is not the case that(A,a)∈f?(M)if and only if(B,b)∈f?(N).

The required isomorphic argument-structures are constructed as follows.LetM=N=N,i.e.,the set of natural numbers.LetFn={F:F ∈P(N),|F|=n}for any 01.Obviously,gis a bijection.Let=N,F0,1and=N,F0,0.Obviously,these two argumentstructures are isomorphic.However,(A,a)∈f?(M)and(B,b)f?(N),becausef?(M)(F0)=1 andf?(N)(F0)=1.Therefore,‘?’ is notlogicalTS.So it is notlogicalF,either.

I claim that‘?’islogicalST.32Sher already points out the conclusion about ‘?’ But she only considers the case in which ‘?’ is of type(e,(e)).([19],p.305)Similarly,Tarski also mentions that it is logical and claims,further,that‘using the method of Principia Mathematica,set theory is simply part of logic.’([22],p.152)So Tarski claims that the definability thesis of Russell’s logicism succeeds,although he does not show in his paper that the quantifiers and propositional connectives are also logical.‘?’is of type(τ,(τ)),whereτ=(...(e)...)(npairs of parenthesis,n?0).I shall show that it islogicalSTin the case thatn=1.It can be shown in the similar way that it islogicalSTwhenn>1.Suppose there are two isomorphic argument-structures of ‘?’and,wherea ∈M,A ?M,b ∈N,B ?N,such that(a,A)∈f?(M)but(b,B)f?(N).Since the structures are isomorphic,there is a bijectiong:M →Nsuch thatg(a)=b,andg(A)=B.Since(a,A)∈f?(M),a ∈A.Thus,g(a)=b ∈g(A)=B.Therefore,the supposition cannot hold.

The constant ‘?’ islogicalF.Otherwise,supposeandare two homomorphic argument-structures of‘?’such that it is not the case that(a,A)∈f?(M) iff (b,B)∈f?(N),wherefis a surjection fromMtoN.Supposea ∈Abutb ∈B.Obviously,this cannot be the case.SupposeaAbutb ∈B.Sinceb ∈Bandg(e)(A)=B,there is somec ∈Athatg(c)=b.Let us show thata ∈A.BecauseAis in the domain ofg(e),it is the case that for allx,y ∈M,ifg(x)=g(y),thenx ∈Aiffy ∈A.g(a)=g(c),sob ∈Aiffa ∈A.Therefore,a ∈A.So we arrive at a contradiction.By the same token,we can show that the constant‘?’is alsologicalFforn>1.

7 Conclusion

Undoubtedly,the provability thesis of Frege-Russellian logicism is certainly unjustifiable.So let us focus on the definability thesis.Insofar as logicality is either isomorphism invariance or homomorphism invariance,the constant ‘?’ for the concept“the number of”is not logical,while all constants in(i.2)are so.Consequently,Boolos’s assessment of Frege’s logicism on p.70 is right.It is easy to show that there are arithmetical concepts that are not isomorphism invariance.Because any homomorphism invariance is also isomorphism invariance,any arithmetical concept that is not isomorphism invariance is not homomorphism invariance.

Let us take 0 as an example of non-isomorphism invariance in Frege’s system.The constant 0 is defined as?[x:xx]in Frege’s system.0 is of typeeand its argument-structures are，wherea ∈MandMis infinite.It holds in any arbitrary domainMthatf?([x:xx])=f?(?)∈M.Supposef?(?)=a ∈M.Therefore,f0(M)=m,i.e.,the numeral 0 denotes the objectainM.LetNbe such a set thatf0(N)=b ∈N,where|N|=|M|.There is a bijectionf:M →Nsuch thatf(a)=c ∈Nandcb.Therefore,andare isomorphic.However,a=f0(M)andcf0(N).Therefore,0 is not isomorphism invariance.

If logicality is isomorphism invariance,then the definability thesis of Russell’s logicism is fully justified,because in the case the claim (+) on p.68 holds for the language of STT.33For more information on the proof of the claim,see[21,pp.384–393].

If logicality is homomorphism invariance,then the definability thesis of Russell’s logicism cannot be fully justified.Higher-order universal quantifiers are notlogicalF,but its corresponding existential quantifiers arelogicalF.Let us replace the higher-order universal quantifiers occurring in the axioms of STT by the corresponding existential quantifiers.Then,all constants in(ii.2)and(ii.3)arelogicalF.34It is worthy of noticing that the constant for identity is also not logicalF.But the constant is not necessary to higher-order logics,because it can be defined in a canonical manner.However,the claim(+)does not hold any more provided that logicality is homomorphism invariance.To see this,let us take the cardinal numeraln2(its denotation is the numbernof type((e)))in STT as an example.

The argument-structure ofn2is (M,A),whereMis any non-empty set andA ?M.(M)={A ?M:|A|=n}if|M|?n; otherwise,(M)=?.LetM={u1,...,un},N={v1,...,vn?1}andf:M →Nbe a surjection thatf(u1)=f(u2)=v1and for 2< m?n,f(um)=vm?1.It is not hard to verify that和are homomorphic,becauseM ∈Dom(f(e)).Obviously,M ∈(M)andN(N).Therefore,n2is not homomorphism invariance.