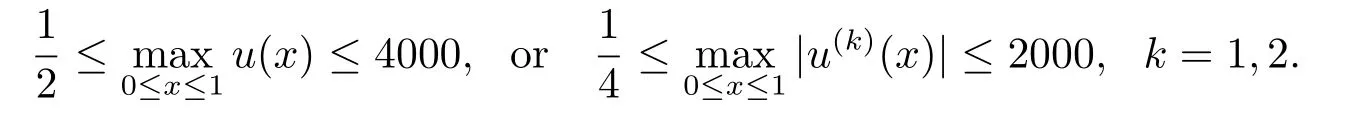On (n?1,1) Conjugate Boundary Value Problems with Dependence on Fully Nonlinearity

LI Zhiyu(李智宇),BAI Zhanbing(白占兵)

(College of Mathematics and System Science,Shandong University of Science and Technology,Qingdao 266590,China)

Abstract: In this paper,a fixed point theorem in a cone and some inequalities of the associated Green’s function are applied to obtain the existence of positive solutions of(n?1,1)conjugate boundary value problems with dependence on all lower order derivatives.

Key words: Conjugate boundary value problem;Fixed point theorem in a cone;Positive solutions

1.Introduction

In recent years,there has been much attention focused on questions of positive solutions of conjugate boundary value problems for nonlinear ordinary differential equations,difference equations,and functional differential equations without dependence on the first order derivative[1,3?6,8,10?11].It is well known that the famous Krasnosel’skii’s fixed point theorem in a cone[5],as well as Leggett-Williams fixed point theorem[6],plays an extremely important role in above works.

However,all the above works were done under the assumption that the derivatives are not involved explicitly in the nonlinear term.For the lower order derivatives which are involved explicitly in the nonlinear term,the study is few[2,9].In this paper,via a generalization of Krasnosel’skii’s fixed point theorem in a cone and some inequalities of the associated Green’s function for the associated problem,we show the existence of positive solutions for the(n?1,1)conjugate boundary value problem

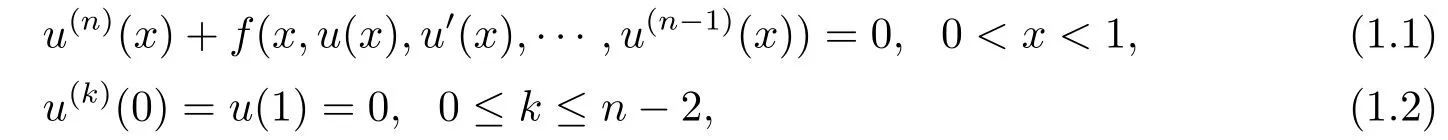
wheren ≥2,f:is continuous.Forn=2,LI[7]studied the problem (1.1)-(1.2) under the conditions that the nonlinearityf(x,u,v) may be superlinear or sublinear growth onuandv.The superlinear and sublinear growth of the nonlinearityfare described by inequality conditions instead of the usual upper and lower limits conditions.The discussion is based on the fixed point index theory on cones.

As it is pointed out in[4],forn=2,positive solutions of Problem(1.1)-(1.2)are concave and this concavity was useful in define a cone on which a positive operator was defined,to which a fixed point theorem due to Krasnosel’skii was then applied to yield positive solutions.For the general problem considered in this paper,the corresponding property was obtained by Eloe et al.[4]with the classical maximum principle.Readers may find that the property is crucial in defining an appropriate cone in this paper such that a generalization of Krasnosel′skii’s fixed point theorem due to BAI and GE[2]can be used to obtain positive solutions.

2.Preliminaries and Lemmas

LetXbe a Banach space andP ?Xis a cone.Supposeα,β:X →R+are two continuous nonnegative functionals satisfying

Lemma 2.1[2]Letr2>r1>0,L2>L1>0 be constants and

Lemma 2.2[4]Letn ≥2 andu∈Cn[0,1] satisfy

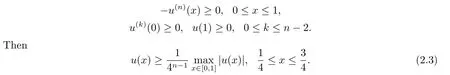
Lemma 2.3[4]LetG(x,s) be Green’s function for the boundary value problem

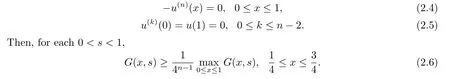
3.Existence Results of Positive Solutions

In this section,we obtain positive solutions of Problem (1.1)-(1.2) by the use of Lemmas 2.1-2.3.

Problem (1.1),(1.2) has a solutionu=u(x) if and only ifusolves the operator equation

So,∥u∥=max{α(u),β(u)},the assumptions (2.1),(2.2) hold.

Denote

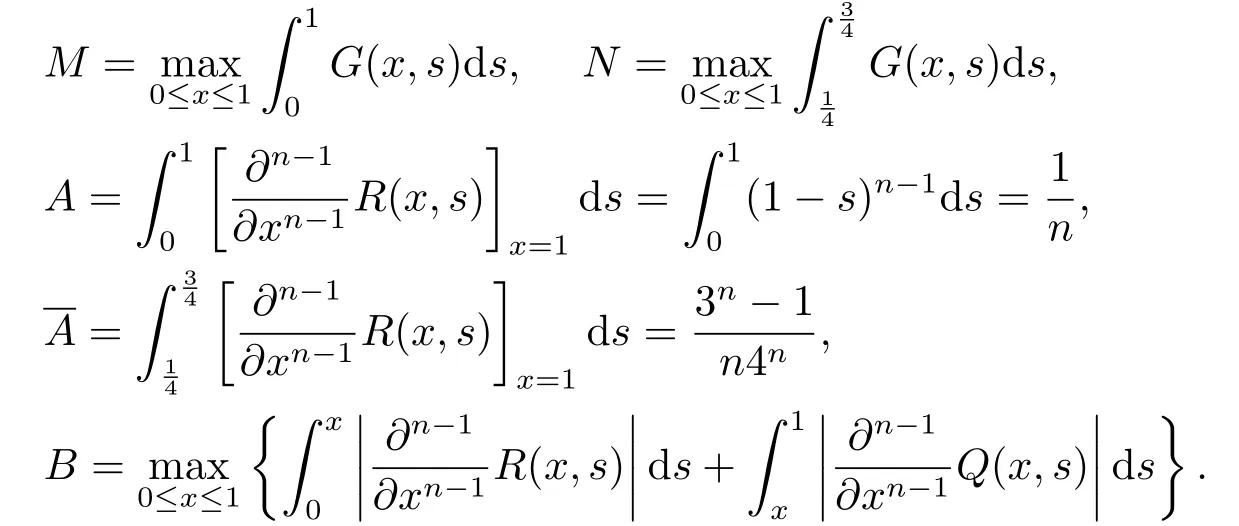
It is well known thatT:P →Pis completely continuous.In fact,ifu∈P,then the continuity offand the property ofG(x,s) yieldsTu ∈Cn?1[0,1].By (2.6),

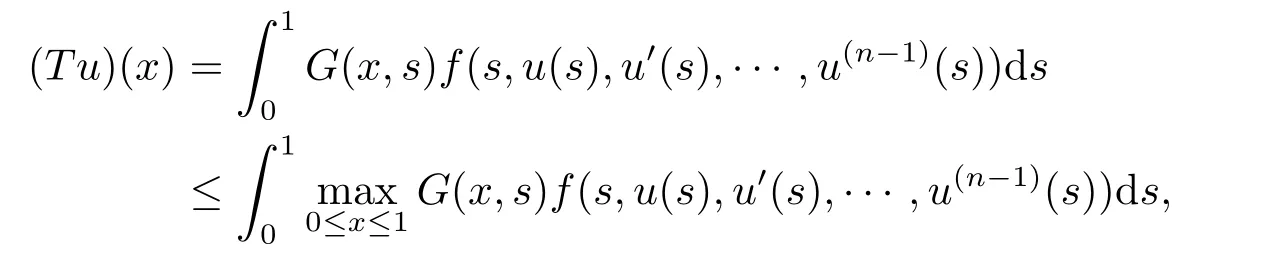
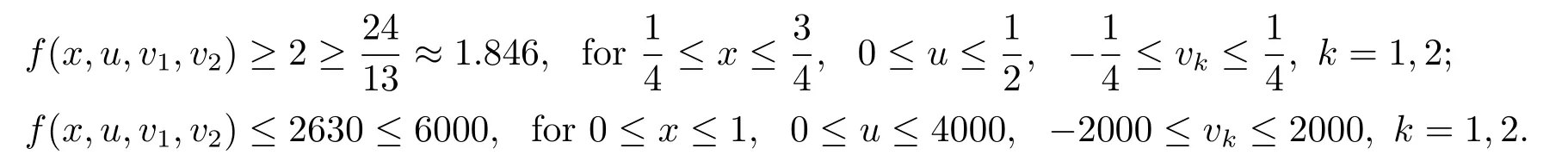
Then all assumptions of Theorem 3.2 hold.

Thus with Theorem 3.2,the problem (4.3)-(4.4) has at least one positive solutionu(x)such that