某類亞純多葉函數(shù)子類的包含性質(zhì)

陳 帆,秦 川,李小飛

(1.長江大學 工程技術(shù)學院,湖北 荊州 434000; 2.長江大學 信息與數(shù)學學院,湖北 荊州 434000; 3.澳門大學 數(shù)學系,澳門 999078)

設∑p表示單位去心圓盤E={z∈C,0<|z|<1}=U{0}內(nèi)具有下列形式

(1)

的p葉解析函數(shù)族, 用Pk(ρ)表示單位圓盤U內(nèi)解析且滿足下列條件的函數(shù)p(z)的集合

(2)

其中：z=reiθ,0≤ρ<1,k≥2.函數(shù)類Pk(ρ)由Padmanabhan等[1]引入并被許多作者研究[2-5].對參數(shù)k,ρ進行取值,得到以下特殊函數(shù)類

(1)Pk=Pk(0)由Pinchuk[6]引入并研究;

(2)P(ρ)=P2(ρ)為實部大于ρ的函數(shù)類,P=P2(0)為正實部函數(shù)類, 由Aouf[7]引入并研究.

容易驗證,p(z)∈Pk(ρ)當且僅當存在函數(shù)p1,p2∈P(ρ)，使得

(3)

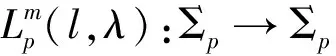
若f(z)∈Σp由(1)式給出, 對μ>0,a-b≥0,El-Ashwah等[9]定義了積分算子函數(shù)

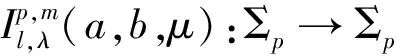
(4)

其中：μ>0,a-pμ>0,b-pμ>0,a-b≥0,l>0,λ>0,m∈N0,p∈N.

(5)

(6)

(7)

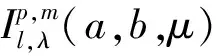
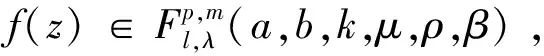
(8)

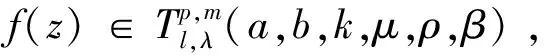
(9)

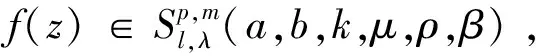
(10)

1 主要結(jié)論

引理1[17]設p(z)在U內(nèi)解析,且p(0)=1,α∈C,Re(α)≥0(α≠0), 若

則

Rep(z)>γ+(1-γ)(2σ-1),

如果不做特殊說明,下文中參數(shù)均滿足條件

μ>0,a-pμ>0,b-pμ>0,a-b≥0,l>0,λ>0,m∈N0,p∈N.

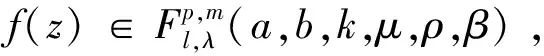
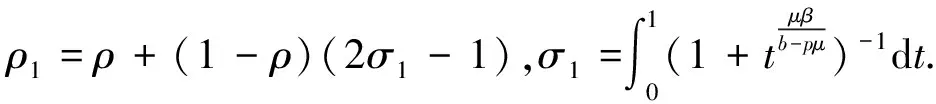
證明記

(11)

則p(z)在U內(nèi)解析.對(11)式兩邊取導數(shù)并運用(5)式,得到

(12)

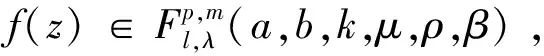
(13)

且滿足

即

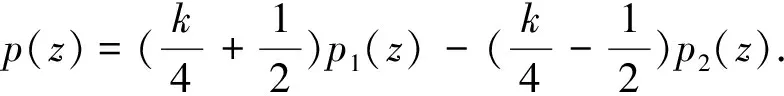
(14)

由引理1和(13)式,得

由于pi(z)∈P(ρ1),i=1,2,由(14)式,p(z)∈Pk(ρ1),即

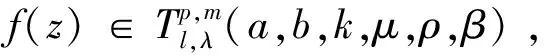
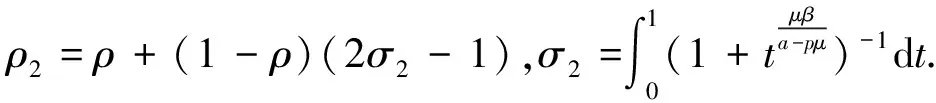
證明記

(15)

則q(z)在U內(nèi)解析.對(15)式兩邊取導數(shù)并運用(6)式,得到

(16)

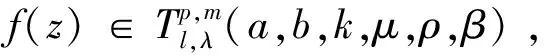
(17)

且滿足

即

(18)

由引理1和(17)式,得

Reqi(z)>ρ2=ρ+(1-ρ)(2σ2-1),

由于qi(z)∈P(ρ2),i=1,2,由(18)式,q(z)∈Pk(ρ2),即

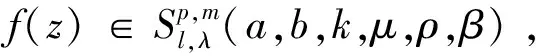
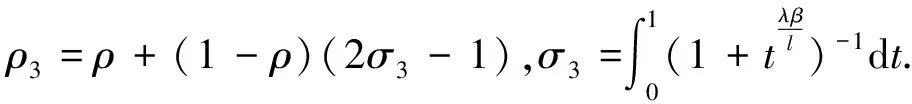
證明記

(19)

則h(z)在U內(nèi)解析.對(19)式兩邊取導數(shù)并運用(7)式,得到

(20)

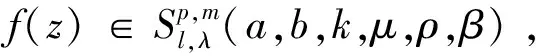
(21)

且滿足

即

(22)

由引理1和(21)式,得

Rehi(z)>ρ3=ρ+(1-ρ)(2σ3-1),

由于hi(z)∈P(ρ3),i=1,2,由(22)式,h(z)∈Pk(ρ3),即

設f(z)∈∑p, 文獻[17]引入了一類新的積分函數(shù)Fβ(z),定義為

容易驗證,Fβ(z)滿足下列性質(zhì)

(23)

(24)

(25)

下面討論關于函數(shù)Fβ(z)的包含關系.

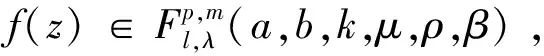
證明由定義知

(26)

對(26)式兩邊取導數(shù)并運用(23)式,得到

(27)

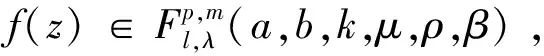
即

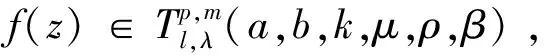
證明由定義知

(28)

對(28)式兩邊取導數(shù)并運用(24)式,得到

(29)

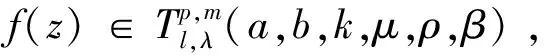
即

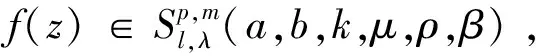
證明由定義知

(30)

對(30)式兩邊取導數(shù)并運用(25)式,得到

(31)

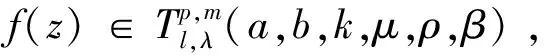
即