The category of upper bounded bifinite posets

Li Jibo,Chen Yanchang,Zhang Haixia

(1.School of Mathematics and Statistics,Anyang Normal University,Anyang 455000,China;2.College of Mathematics and Information Science,He′nan Normal University,Xinxiang 453007,China)

Abstract：In this paper,some results about D-precontinuous or D-prealgebraic posets and D△-continuous functions are summarized and supplemented.The category BFBP,in which objects are upper bounded bifinite posets and arrows are D△-continuous functions between them,is shown to be cartesian closed.

Keywords： D-precontinuous posets,D-prealgebraic posets,D△-continuous functions,Cartesian closed categories

1 Introduction

The study of cartesian closed categories has received considerable attention in the study of domain theory.Related issues were dealt with in reference[1-8].Because the category DOM of domains and Scott continuous maps is not cartesian closed,many researchers looked for full subcategories of DOM,and in particular for maximal ones.References[2-3]successfully identified all maximal cartesian closed full subcategories of DOM.Among the maximal ones is the category of FS-domains.Later,the category of bifinite domains is considered in reference[9].

Classically,domain theory is based on the investigation ofdcpos in which every directed set has a least upper bound.However,there are important ordered structures which fail to be dcpos and more and more occasions to study posets which are not directed complete.To get rid of the restriction to directed sets,in references[10-11]generalized the concept of FS-domains and bifinite domains to the FS-posets and B-posets,respectively.Some elementary results about FS-posets,B-posets and relevant categories have been obtained in reference[10].In reference[12],the authors introduced the concept of finitely separated and upper bounded posets and proved that the category FSBP is cartesian closed in which objects are finitely separated and upper bounded posets,and arrows areD△-continuous functions between them.To make the study deeper,in this paper,some results aboutD-precontinuous orD-prealgebraic posets andD△-continuous functions are summarized and supplemented.The category BFBP is shown to be cartesian closed,in which objects are upper bounded bifinite posets and arrows areD△-continuous functions(or,Scott continuous functions by Proposition 2.1)between them.

2 Preliminaries

LetPbe a poset andYa subset ofP.We denote the set{x∈P|?y∈Y,x≤y}by↓Y,and the set↑Yis defined dually.IfY=↓Y,thenYis called a downset or lower set;the dual is an upset or upper set.In particular,the set↓x=↓{x}(resp.,↑x=↑{x})is called the principal ideal(resp.,principal dual ideal)generated by the elementx.The cut operator△onPis defined by△Y=∩{↓x|x∈P,Y?↓x}for everyY?P.

For a posetP,letAPdenote the collection of all lower subsets ofPandDPthe collection of all directed subsets ofP.The cut operator△gives rise to a standard completionD△PofP:D△P={Y∈AP|D∈DPandD?Yimply△D?Y}.Note that△X∈D△Pfor everyX?P.TheD-below ideal generated by an elementy∈Pis the set?Dy=∩{D∈DP∩AP|y∈△D}.Forx,y∈P,we writex?Dyifx∈?Dy,that is,D∈DPandy∈△Dimplyx∈↓D.Obviously,theD-below relation is an auxiliary relation in the sense of[1].An elementx∈Psatisfyingx?Dxis calledD-compact.The subset of allD-compact elements is denoted byKDP.A posetPis calledD-precontinuous if?Dy∈DPandy=∨?Dyfor eachy∈P.If↓y∩KDP∈DPandy= ∨(↓y∩KDP)for everyy∈P,thenPis said to beD-prealgebraic.It is clear that everyD-prealgebraic poset isD-precontinuous.

Lemma 2.1A posetPisD-precontinuous provid∨ed that,for everyy,one can find a directed setDof elementsd?Dysuch thaty=D.

ProofLetu?Dy,v?Dy.Thenu≤duandv≤dvfor somedu,dv∈D.Pickd∈Dsuch thatdu≤danddv≤d.Thenu≤d,v≤dandd?Dy.Thus?Dyis directed.Sincey= ∨Dand any upper bound of?Dyis an upper bound ofD,we know thaty=∨?Dy.The remaining part of the statement is easy.

Let us note that aD-precontinuous(resp.,D-prealgebraic)dcpo is just a domain(resp.,algebraic domain),but aD-precontinuous(resp.,D-prealgebraic)poset is not the same thing as a continuous(resp.,algebraic)poset in the sense of[1],for example,the Euclidean plane R2under the usual order is a continuous poset,but it is not aD-precontinuous poset and the poset Z2under the usual order is an algebraic poset,but it is not aD-prealgebraic poset.

Turn to certain classes of functions between two posets.Letfbe a function between posetsPandQ.The functionfis calledD△-continuous iff?1(Y)∈D△Pfor allY∈D△Q,and weaklyD△-continuous if at leastf?1(↓x)∈D△Pfor allx∈Q.

Proposition 2.1[12-13]For a functionfbetween posetsPandQ,consider the following conditions:

(1)fisD△-continuous;

(2)fis weaklyD△-continuous;

(3)f(△D)?△f(D)for eachD∈DP;

(4)f(∨D)= ∨f(D)for everyD∈DPwhich has a join inP.

The implications(1)?(2)?(3)?(4)are true,and(3)?(4)holds ifPisD-prealgebraic.

Proposition 2.2LetSbe aD-precontinuous poset andp:S→SaD△-continuous projection.Then the imagep(S)with the order induced fromSis aD-precontinuous poset,too.Forx,y∈p(S),

ProofLety∈p(S)be given.AsSisD-precontinuous,the setis directed and∨.SincepisD△-continuous,we know from Proposition 2.1 that it preserves directed joins,whenceis directed and.Asy∈p(S),we havep(y)=y.In accordance with Lemma 2.1,for theD-precontinuity ofp(S),it suffices to prove thatp(u)wheneveru.For this,letube an element ofSsuch thatu.Consider any directed subsetD?p(S)such thaty∈△D.Asu,we can find ad∈Dsuch thatu≤d.Thenp(u)≤p(d)=dby the monotonicity and idempotency ofp.This shows thatp(u).For the second part of the claim,letx,y∈p(S)such thatx.Asby the above,there is au∈Swithusuch thatx≤p(u).The converse has already been shown in the first part of the proof.

Proposition 2.3LetPbe a poset andS=δ(P)the image of aD△-continuous kernel operatorδ:P→P.Then an elementx∈SisD-compact inSi ffxisD-compact inP,that isKD(S)=S∩KD(P).

ProofAs in the proof of Proposition 2.2,we see that for an elementx∈S,xisD-compact inSwhen it isD-compact inP.For the converse,letx∈SbeD-compact inS.Consider any directed subsetD?Psuch thatx∈△D.Under the hypothesis thatδ:P→Pis aD△-continuous kernel operator,we getδ(D)is a directed subset ofSandx=δ(x)∈δ(△D)?△δ(D).AsxisD-compact inS,there exists ad∈Dsuch thatx≤k(d).Sinceδis a kernel operator,we havex≤d.This shows thatxisD-compact inP.

Henceforth,we restrict our considerations to upper bounded posets,which guarantees that in directed productsR×S,the cut operator satisfies△(Y1×Y2)=△Y1×△Y2forY1?RandY2?S.Generally speaking,this equation is false,as is shown in the Euclidean plane R2.

LetS,Tbe posets and denote theD△-continuous function space by[S→T]Dor simply by[S→T].Forf,g∈[S→T],we definef≤gi fff(x)≤g(x)for eachx∈S.Then[S→T]is a poset.

Lemma 2.2[12]GivenD△-continuous mapsδ∈[R→R]andε∈[S→S]on upper bounded posets.Then the mapδ×ε:R×S→R×S,(r,s)7→(δ(r),ε(s))is againD△-continuous.

Proposition 2.4[12]LetR,Sbe upper bounded posets,then the evaluation mape:[R→S]×R→S,(f,r)7→f(r)isD△-continuous.

Proposition 2.5[12]LetRbe an arbitrary poset andS,Tbe upper bounded posets,then the composition mapc:[S→T]×[R→S]→[R→T],(f,g)7→f?gisD△-continuous.

Proposition 2.6[12]LetR,S,Tbe upper bounded posets,and defineE,Fby

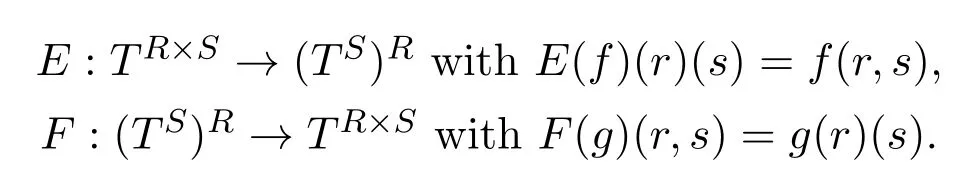
Then the bijectionsEandFinduce mutually inverse isomorphisms between the upper bounded posets[(R×S)→T]and[R→[S→T]].

3 The category upper bounded bifinite posets

Recall that for a posetS,a△-approximate identity is a directed setD?[S→S]satisfying ∨D=idS,the identity onS.AD△-continuous functionδ:S→Sis finitely separating if there exists a finite setFδ?Ssuch that for eachx∈S,there is ay∈Fδwithδ(x)≤y≤x.A posetSis finitely separated if there is a△-approximate identity forSconsisting of finitely separating functions.

Lemma 3.1[12]LetPbe a poset.Ifδ∈[P→P]is finitely separating,thenδ(x)?Dxfor allx∈P.

Definition 3.1AD-prealgebraic finitely separated poset is called a bifinite poset.A bifinite upper bounded poset will be called a BFB-poset.

Proposition 3.1For an upper bounded posetP,the following properties are equivalent.

(1)Pis a bifinite poset;

(2)Pis aD-prealgebraic poset and has a△-approximate identity consisting of functions with finite range;

(3)Phas a△-approximate identity consisting of kernel operators with finite range.

ProofThe implication(2)?(1)is immediate.For the implication(3)?(2),it suffices to show that(3)implies thatPisD-prealgebraic.For this,letDbe a directed set ofD△-continuous kernel operators with finite range such that∨D=idP.Then the setS={δ(x)|δ∈D}is directed.The greatest element ofPis denoted by 1P.Next,we will show that the join of the setSexists and isx.It is very clear thatxis an upper bound ofS.Suppose thatuis an arbitrary upper bound ofS.Define a maph:P→Pas follows:

Thenhis well defined.It is clear thathisD△-continuous andδ≤hfor everyδ∈D.Thus∨D≤hin[P→P].As∨D=idP,we havex=(∨D)(x)≤h(x)=u.This shows thatx= ∨S.As the imageim δ={δ(x)|x∈P}ofδ∈Dis finite,all of its elements areD-compact in the finite posetim δ.From Proposition 2.3,it follows that all the elements ofim δareD-compact inP.Thus,everyx∈Pis the join of a directed set ofD-compact elements and we have shown thatPisD-prealgebraic.

Now establish that(1)implies(3).LetDbe a△-approximate identity onPsuch that eachδ∈Dis finitely separating.For eachδ∈D,setGδ={k∈P|δ(k)=k}.Note that it must be the case thatGδ?Fδ,which is the finite separating set,and hence,Gδis finite.Moreover,all elements ofGδareD-compact by Lemma 3.1.

We claim that for eachx∈P,there exists a largest member ofGδin↓x.In fact,we can pick a minimal elementzof↓x∩Fδsince↓x∩Fδis a nonempty finite set under the hypothesis thatδis finitely separating.Then there exists a member ofFδbetweenδ(z)andδ(δ(z)),and this must bezby minimality ofz.It follows thatz=δ(z).Thus↓x∩Gδ?.

Letk1,k2∈↓x∩Gδ.Thenki=δ(ki)≤δ(x)fori=1,2.There existsy∈Fδsuch thatδ(x)≤y≤x,and thuski≤y≤xfori=1,2.Pick a minimal elementk∈↓x∩Fδsuch thatki≤kfori=1,2.Thenki=δ(δ(ki))≤δ(δ(k))≤δ(k)fori=1,2.Asδis finitely separating,there must be an element ofFδbetweenδ(δ(k))andδ(k),and this element must be equal tokby minimality ofk.It follows thatδ(k)=k.Thus the finite set↓x∩Gδis directed,and hence,it must have a largest element.

Forδ∈D,defining a functionkδbykδ(x)is the largest compact elementk≤xsuch thatδ(k)=k.The preceding paragraphs guarantee the existence of such a function.One verifies easily thatkδis aD△-continuous kernel operator with finite range.Also the family{kδ|δ∈D}is directed,since asδbecomes larger,the setGδof fixed-points grows.Next,we will show that the join of the family{kδ|δ∈D}exists and it is equal to idP,that is{kδ|δ∈D}is a△-approximate identity.For this,letx∈P.In casex∈KD(P),sinceDis a△-approximate identity,there existsη∈Dsuch thatδ(x)=xfor anyδ≥η,and hence,x=∨{kδ(x)|δ∈D}.In casex/∈KD(P).AsPisD-prealgebraic,we obtainx= ∨(↓x∩KD(P)).From Proposition 2.1,it follows thatkδ(x)= ∨kδ(↓x∩KD(P)).Note that

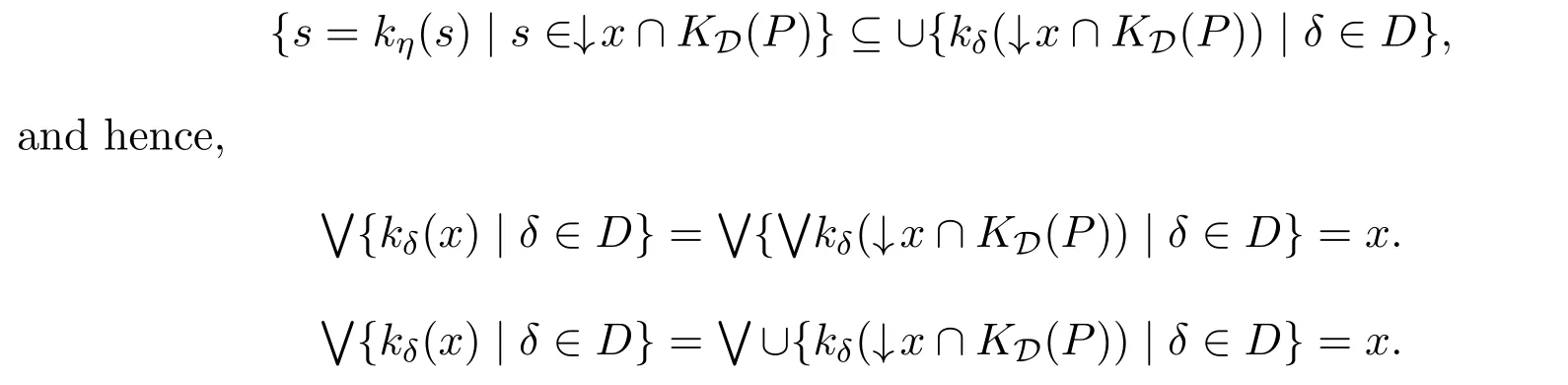
Define a functionf:P→Pbyf(x)= ∨{kδ(x)|δ∈D}.ThenfisD△-continuous and hence,∨{kδ|δ∈D}=f=idP.

Proposition 3.2IfRandSare BFB-posets,thenR×Sand[R→S]are also BFB-posets.

ProofIt is obvious thatR×Sand[R→S]are upper bounded posets.LetDandEbe△-approximate identity forRandS,respectively,consisting of kernel operators with finite range(see Proposition 3.1(3)).By Lemma 2.2,δ×εisD△-continuous for anyδ∈D,ε∈E.ThenD×E={δ×ε|δ∈D,ε∈E}clearly is a△-approximate identity forR×Sconsisting of functions with finite range andR×SisD-prealgebraic,thusR×Sis a BFB-poset by Proposition 3.1.Next we will show that[R→S]is a BFB-poset.For this,letδ∈Dandε∈E.Define a self-map

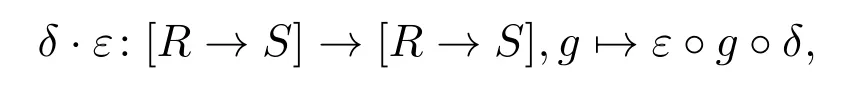
and denoteD⊙E={δ·ε|δ∈D,ε∈E}.Forδ1·ε1andδ2·ε2inD⊙E,there existδ3∈Dandε3∈Esuch thatδ1≤δ3,δ2≤δ3,ε1≤ε3andε2≤ε3.By monotonicity of the involved functions,it follows thatδi·εi≤δ3·ε3fori=1,2.Therefore,D⊙Eis a directed set.

Iterated application of Proposition 2.5 and related simpler continuity arguments show that the compositeg 7→δ·εisD△-continuous.For eachg∈[R→S],r∈R,we infer

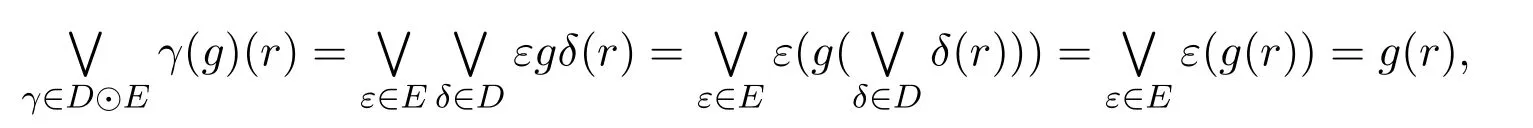
that is,∨D⊙E=1[S→T].Thus,the familyD⊙Eis a△–approximate identity for[S→T].Asδandεare idempotent,the same follows forδ·εand consequently this is a kernel operator.Its range is finite,as it can be viewed to be the set of all monotone maps from the finite posetim δinto the finite posetim ε.Thus,D⊙Eis a△-approximate identity on[R→S]consisting of kernel operators with finite range,which implies that[R→S]is a BFB-poset.

Proposition 3.3LetR,S,Tbe BFB-posets,and defineE,Fby

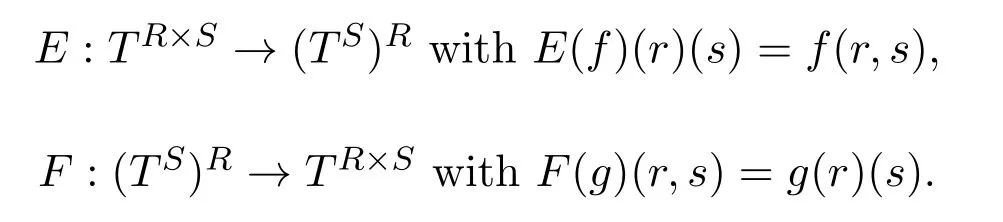
Then the bijectionsEandFinduce mutually inverse isomorphisms between the BFB-posets[(R×S)→T]and[R→[S→T]].

ProofThis follows immediately from Proposition 2.6 and Proposition 3.2.

Now we are ready to study the category BFBP of all BFB-posets andD△-continuous maps between them.Given a BFB-posetS,the preceding results give rise to two functors from the category BFBP to the category SET of sets:

The product functor?×S:BFBP→SET sends each objectRof BFBP toR×Sand each morphismf:R→R′tof×idS.

The exponent functor[S→?]:BFBP→SET sends each objectTof BFBP to[S→T]and each morphismf:T→T′tof??:[S→T]→[S→T′].

Proposition 3.3 indicates that for three objectsR,S,Tin BFBP,the contravariant hom-functorshom(?×S,T)andhom(?,[S→T])from BFBPopto SET are naturally isomorphic,and the hom-functorshom(R×S,?)andhom(R,[S→?])from BFBP to SET are naturally isomorphic,too(refer to reference[13]for background on homfunctors).In all,the following isomorphismEis natural inRandT:

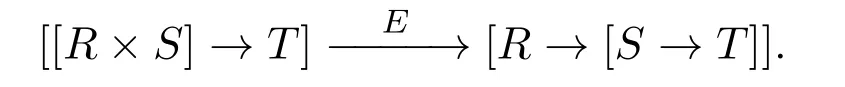
In fact,leth:R′→Randk:T→T′.Then for anyf:R×S→T,an easy direct computation yieldsE(f?h×idS)=E(f)?handE(k?f)=[S→?](k)?E(f).For the first equality,givenr′∈R′,s∈S,we have:

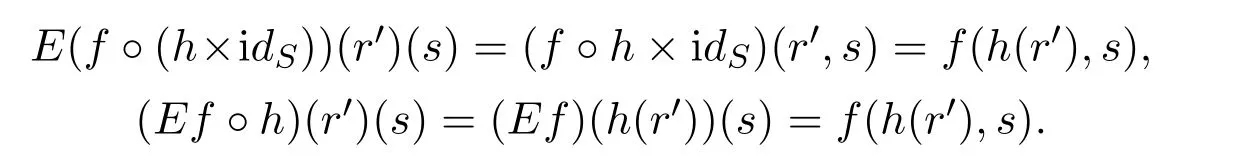
For the second equality,givenr∈R,s∈S,we have:

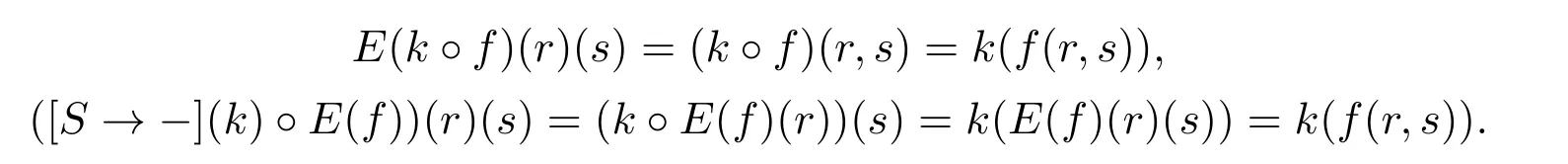
Summarizing the previous facts,we arrive at

Theorem 3.1The category BFBP is cartesian closed.

ProofIn the category BFBP,any singleton poset is a terminal object.Each pair of objectsRandShas a productR×Swith the obvious projectionsp1∈[R×S→R]andp2∈[R×S→S].

LetR,S,Tbe three objects in the category BFBP.There is an object[R→S]and an arrowe∈[[S→T]×S→T]with the property that for any arrowf:[R×S→T],there is a unique arrowE(f)∈[R→[S→T]]such that the composite

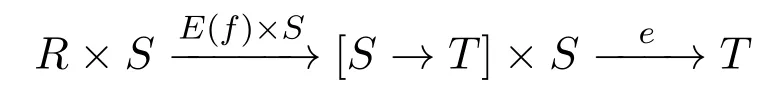
is justfby Proposition 2.4 and Proposition 3.3.Thus the category BFBP is cartesian closed.