AN ESTIMATE FOR MAXIMAL BOCHNER-RIESZ MEANS ON MUSIELAK-ORLICZ HARDY SPACES
WANG Wen-hua, QIU Xiao-li, WANG Ai-ting, LI Bao-de
(College of Mathematics and System Science, Xinjiang University, Urumqi 830046, China)
Abstract: In this paper, we study the boundedness of maximal Bochner-Riesz means. By using the pointwise of maximal Bochner-Riesz means and the atomic decomposition of weak Musielak-Orlicz Hardy space, we establish the boundedness of maximal Bochner-Riesz means from weak Musielak-Orlicz Hardy space to weak Musielak-Orlicz space. This result is new even when ?(x, t):=Φ(t) for all (x, t)∈Rn×[0, ∞), where Φ is an Orlicz function, and it is an extension to Musielak-Orlicz spaces from the setting of the weighted spaces of Wang [1].
Keywords: Bochner-Riesz means; Muckenhoupt weight; Orlicz function; Hardy space
1 Introduction
The Bochner-Riesz means of order δ ∈(0, ∞)are defined initially for Schwartz functions f on Rnby, for any x ∈Rn,
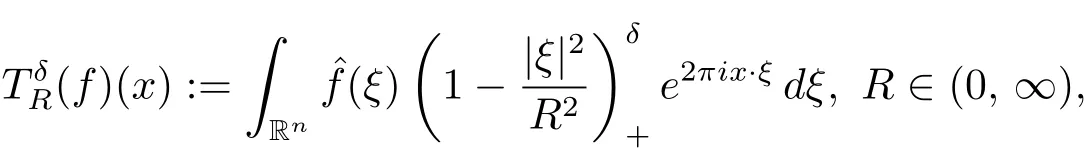
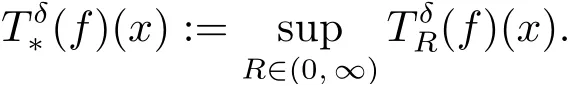
The Bochner-Riesz means were first introduced by Bochner[2]in connection with summation of multiple Fourier series. Questions concerning the convergence of multiple Fourier series led to the study of their Lp(Rn) boundedness.
In 2013,Wang[1]considered the values of δ greater than the critical index n/p?(n+1)/2 and proved the following weighted weak type estimate ofwhich is bounded from weighted weak Hardy spaceto weighted weak Lebesgue space
Theorem ALet p ∈(0, 1]and δ ∈(n/p?(n+1)/2, ∞). If ω ∈A1(the Muckenhoupt weight class), then there exists a positive constant C independent of f such that
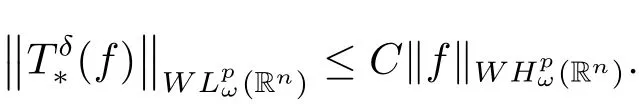
Recently,Liang et al.[3]introduced weak Musielak-Orlicz Hardy space WH?(Rn),which generalizes both the weak Orlicz-Hardy space and the weak weighted Hardy space,and hence has a wide generality. In light of Wang[1] and Liang et al.[3], it is a natural and interesting problem to ask whetheris bounded from WH?(Rn)to WL?(Rn). In this paper,we shall answer this problem affirmatively.
Precisely, this paper is organized as follows.
In Section 2,we recall some notions concerning Muckenhoupt weights,growth functions and weak Musielak-Orlicz Hardy space WH?(Rn). Then we present the boundedness of maximal Bochner-Riesz meansfrom WH?(Rn) to WL?(Rn) (see Theorem 2.6 below),the proof of which are given in Sections 3. This result is also new even it comes back to Orlicz Hardy space.
In the process of the proof of main result, it is worth pointing out that a more subtle pointwise estimate ofon atom (see Lemma 3.5 below) plays a crucial role for the desired estimate of. Moreover, towards the boundedness of maximal Bochner-Riesz meansfrom WH?(Rn) to WL?(Rn), the range of δ (see Theorem 2.6 below) coincides with that of the known best conclusion of Theorem A even ?(x, t):=ω(x)tpfor all (x, t)∈Rn×[0, ∞)with p ∈(0, 1].
Finally,we make some conventions on notation. Let Z+:={1, 2, ···}and N:={0}∪Z+.For any α := (α1,··· ,αn) ∈Nn, let |α| := α1+···+αn. Throughout the whole paper, we denote by C a positive constant which is independent of the main parameters, but it may vary from line to line. The symbolmeans thatand FD,we then write D ~F. For any sets E, F ?Rn, we useto denote the set RnE,|E| its n-dimensional Lebesgue measure and χEits characteristic function. For any a ∈R,denotes the maximal integer not larger than a. If there are no special instructions, any space X(Rn) is denoted simply by X. For example, Lp(Rn) is simply denoted by Lp. For any index q ∈[1, ∞], we denote byits conjugate index, namely, 1/q +1. For any set E of Rn, t ∈[0, ∞) and measurable function ?, letdx and{|f| > t} := {x ∈Rn: |f| > t}. As usual we use Brto denote the ballwith r ∈(0, ∞).
2 Notion and Main Results
In this section, we first recall the notion concerning the weak Musielak-Orlicz Hardy space WH?via the grand maximal function, and then present the boundedness of maximal Bochner-Riesz meansfrom WH?to WL?.
Recall that a function Φ : [0, ∞) →[0, ∞) is called an Orlicz function, if it is nondecreasing, Φ(0)=0, Φ(t)>0 for any t ∈(0, ∞), andAn Orlicz function Φ is said to be of lower (resp. upper) type p with p ∈(0, +∞), if there exists a positive constant C :=Cpsuch that for any t ∈[0, ∞) and s ∈(0, 1] (resp. s ∈[1, ∞)),

Given a function ?:Rn×[0, ∞)→[0, ∞)such that for any x ∈Rn,?(x, ·)is an Orlicz function, ? is said to be of uniformly lower (resp. upper) type p with p ∈(0, +∞), if there exists a positive constant C :=Cpsuch that, for any x ∈Rn, t ∈[0, ∞)and s ∈(0, 1](resp.s ∈[1, ∞)), ?(x, st) ≤Csp?(x, t). The critical uniformly lower type index of ? is defined by
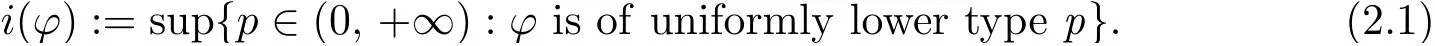
Observe that i(?)may not be attainable,namely,? may not be of uniformly lower type i(?)(see [4, p.415] for more details).
Definition 2.1[5, p.120] Let q ∈[1, ∞). A function ?(·, t) : Rn→[0, ∞) is said to satisfy the uniform Muckenhoupt condition, denoted by ? ∈Aq, if there exists a positive constant C such that for any ball B ?Rnand t ∈(0, ∞), when q ∈(1,∞),
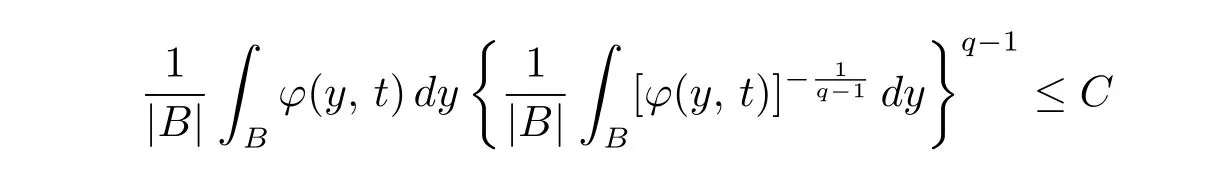
and, when q =1,
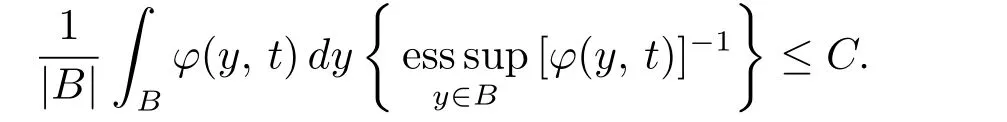
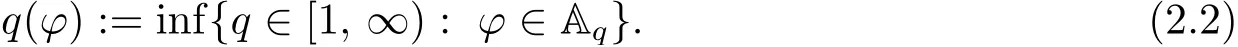
Observe that, if q(?)∈(1, ∞), then ? /∈Aq(?), and there exists ? /∈A1such that q(?)=1(see, for example, [6]).
Definition 2.2[5, Definition 2.1] A function ? : Rn×[0, ∞) →[0, ∞) is called a growth function if the following conditions are satisfied
(i) ? is a Musielak-Orlicz function, namely,
(a) the function ?(x, ·):[0, ∞)→[0, ∞) is an Orlicz function for all x ∈Rn,
(b) the function ?(·, t) is a Lebesgue measurable function on Rnfor all t ∈[0, ∞);
(ii) ? ∈A∞;
(iii) ? is of uniformly lower type p for some p ∈(0, 1] and of uniformly upper type 1.
Clearly, ?(x, t):=ω(x)Φ(t) is a growth function if ω ∈A∞(the Musielak weight class)and Φ is an Orlicz function of lower type p for some p ∈(0, 1] and of upper type 1. It is well known that, for p ∈(0, 1], if Φ(t) := tpfor all t ∈[0, ∞), then Φ is an Orlicz function of lower type p and of upper p; for p ∈[1/2, 1], if Φ(t):=tp/ln(e+t)for all t ∈[0, ∞), then Φ is an Orlicz function of lower type q for q ∈(0, p) and of upper type p; for p ∈(0, 1/2],if Φ(t) := tpln(e+t) for all t ∈[0, ∞), then Φ is an Orlicz function of lower type p and of upper type q for q ∈(p, 1]. Recall that if an Orlicz function is of upper type p ∈(0, 1), then it is also of upper type 1. Another typical and useful growth function is
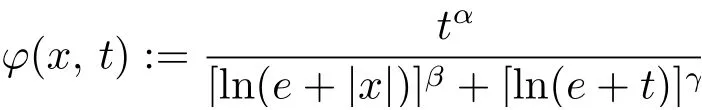
for all (x, t) ∈Rn×[0, ∞) with any α ∈(0, 1], β ∈[0, ∞) and γ ∈[0, 2α(1+ln 2)]; more precisely, ? ∈A1, ? is of uniformly upper type α and i(?)=α which is not attainable (see[5]).
Recall that the Musielak-Orlicz space L?is defined to be the set of all measurable functions f such that for some λ ∈(0, ∞),

equipped with the (quasi-) norm
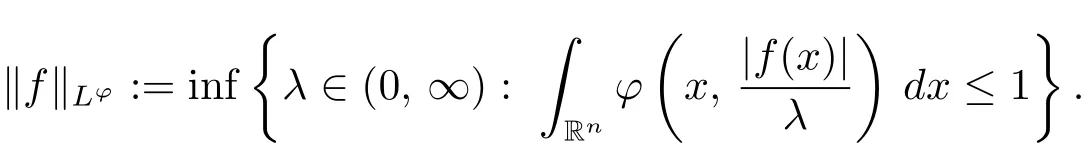
Similarly,the weak Musielak-Orlicz space WL?is defined to be the set of all measurable functions f such that for some λ ∈(0, ∞),
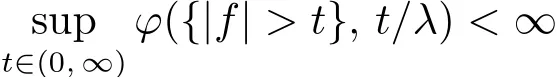
equipped with the quasi-norm

Remark 2.3Let ω be a classical Muckenhoupt weight and Φ an Orlicz function.
(i) If ?(x, t):=ω(x)tpfor all(x, t)∈Rn×[0, ∞)with p ∈(0, ∞),then L?(resp. WL?)is reduced to weighted Lebesgue space(resp. weighted weak Lebesgue space), and particularly, when ω ≡1, the corresponding unweighted spaces are also obtained.
(ii) If ?(x, t):=ω(x)Φ(t) for all (x, t)∈Rn×[0, ∞), then L?(resp. WL?) is reduced to weighted Orlicz space(resp. weighted weak Orlicz space), and particularly,when ω ≡1, the corresponding unweighted spaces are also obtained.
In what follows, we denote by S the space of all Schwartz functions and byits dual space (namely, the space of all tempered distributions). For any m ∈N, let



Definition 2.4[5, Definition 2.2] Let ? be a growth function as in Definition 2.2.The weak Musielak-Orlicz Hardy space WH?is defined as the set of allsuch that f?∈WL?equipped with the quasi-norm
Remark 2.5Let ω be a classical Muckenhoupt weight and Φ an Orlicz function.
(i) If ?(x, t):=ω(x)tpfor all(x, t)∈Rn×[0, ∞)with p ∈(0, 1],then WH?is reduced to weighted weak Hardy spaceand particularly, when ω ≡1, the corresponding unweighted spaces are also obtained.
(ii) If ?(x, t):=ω(x)Φ(t)for all(x, t)∈Rn×[0, ∞),then WH?is reduced to weighted weak Orlicz Hardy spaceand particularly,when ω ≡1,the corresponding unweighted spaces are also obtained.
The main results of this paper are as follows, the proof of which are given in Section 3.
Theorem 2.6Let p ∈(0, 1], δ ∈(n/p ?(n+1)/2, ∞) and ? be a growth function as in Definition 2.2, which is of uniformly lower type p and of uniformly upper type 1. If ? ∈A1, then there exists a positive constant C independent of f such that
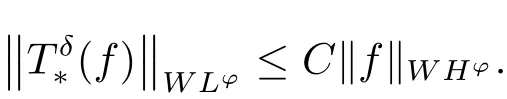
Corollary 2.7Let p ∈(0, 1], δ ∈(n/p?(n+1)/2, ∞), ω be a classical Muckenhoupt weight and Φ an Orlicz function, which is of uniformly lower type p and of uniformly upper type 1. If ω ∈A1, then there exists a positive constant C independent of f such that
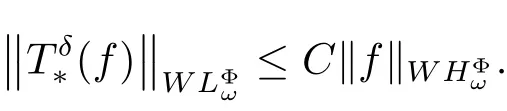
Remark 2.8Let ω be a classical Muckenhoupt A1weight and Φ an Orlicz function.
(i) When ?(x, t) := ω(x)tpfor all (x, t) ∈Rn× [0, ∞) with p ∈(0, 1], we haveTheorem 2.6 is reduced to Theorem A.
(ii) When ?(x, t):=ω(x)Φ(t) for all (x, t)∈Rn×[0, ∞), we have, and particularly, when ω ≡1, the corresponding result on unweighted space is also obtained.
3 Proof of Theorem 2.6
To prove Theorem 2.6,we need some auxiliary lemmas. Let us begin with some notions.
For any measurable set E of Rn, the spacefor q ∈[1, ∞] is defined as the set of all measurable functions f on E such that
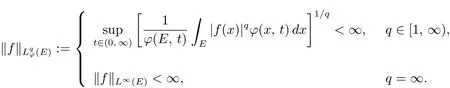
Definition 3.1[3, Definition 3.1] Let ? be a growth function as in Definition 2.2.
(i) A triplet (?, q, s) is said to be admissible, if q ∈(q(?), ∞] and s ∈[m(?), ∞)∩N,where q(?) and m(?) are as in (2.2) and (2.4), respectively.
(ii) For an admissible triplet(?, q, s),a measurable function a is called a(?, q, s)-atom associated with some ball B ?Rnif it satisfies the following three conditions
(a) supp a ?B;
(b)
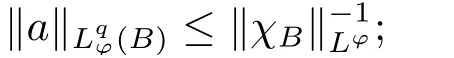
(iii) For an admissible triplet (?, q, s), the weak Musielak-Orlicz atomic Hardy space Wis defined as the set of all f ∈Ssatisfying that there exist a sequence of(?, q, s)-atoms,associated with balls, and a positive constant C such thatfor all x ∈Rn, and i ∈Z, andi nwherefor all i ∈Z and j ∈N, C is a positive constant independent of f.
Moreover, define

where the first infimum is taken over all admissible decompositions of f as above.
Lemma 3.2[7, Lemma 6] Let p1∈(0, 1), δ := n/p1?(n+1)/2 and α ∈Nn. Then there exists a positive constant C :=Cn,p1,αsuch that the kernel φ of Bochner-Riesz means of order δ satisfies the inequality
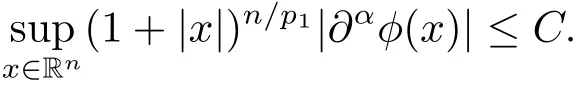
Lemma 3.3[3, Theorem 3.5] Let (?, q, s) be an admissible triplet as in Definition 3.1.Then WH?=with equivalent quasi-norms.
Lemma 3.4[5,Lemma 4.5(i)] Let ? ∈Aqwith q ∈[1, ∞). Then there exists a positive constant C such that for any ball B ?Rn, λ ∈(1, ∞) and t ∈(0, ∞),

Lemma 3.5Let p ∈(0, 1), δ := n/p ?(n+1)/2 and ? be a growth f unction as in Definition 2.2, which is of uniformly lower type p and of uniformly upper type 1. Suppose b is a multiple of a-atom associated with some ball B(x0, r), where q(?) is as in (2.2). Then there exists a positive constant C independent of b such that, for any x ∈Rn,
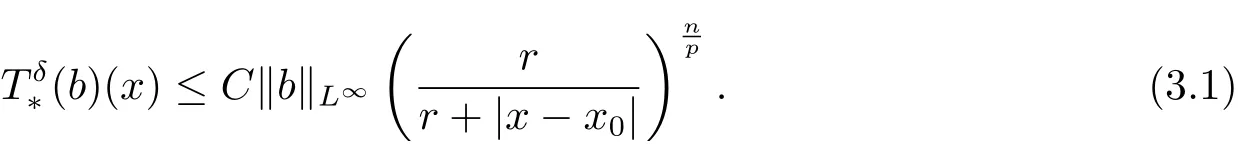
ProofWe show this lemma by borrowing some ideas from the proof of [8, Lemma 2]. It suffices to show (3.1) holds for x0=0and r = 1. Indeed, for any multiple of a-atom b associated with some ball B(x0, r), it is easy to see that
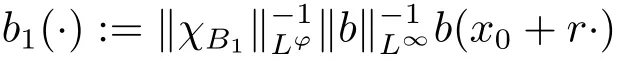

which implies that
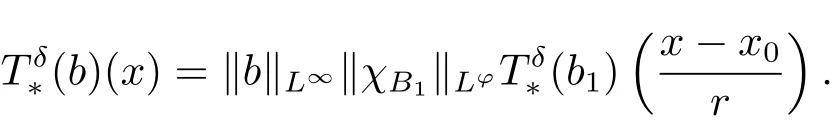
If we assume (3.1) holds for x0=0and r =1, then, for any x ∈Rn, we obtain

It remains to prove(3.1)holds for x0=0and r =1. Let b be a multiple of a-atom associated with the ball B(0,1). From Lemma 3.2 and p ∈(0, 1),we deduce that,for any x ∈B(0,2),
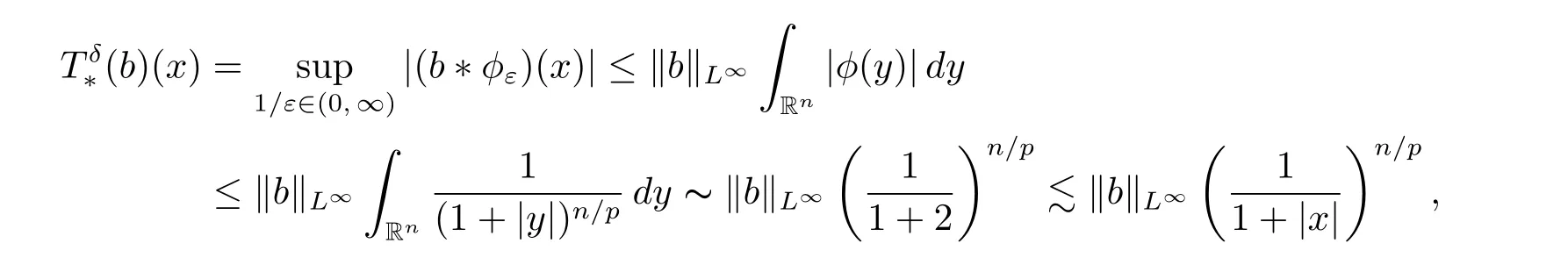
which is wished.
By repeating the estimate of (2) in the proof of [8, Lemma 2], we know that, for any x ∈and ε ∈(0, ∞),
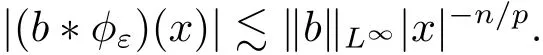
From this and the inequality |x| ~|x| + 1 withit follows that, for any
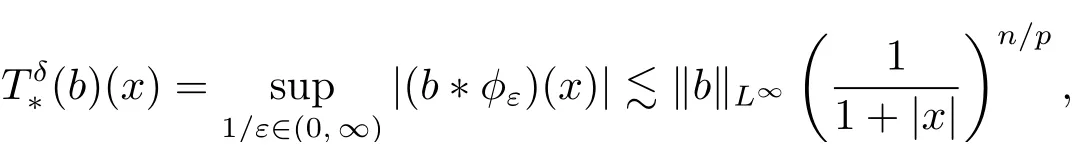
which is also wished. This finishes the proof of Lemma 3.5.
Lemma 3.6[5, Lemma 4.5 (ii)] Let ? ∈Aqwith q ∈(1, ∞). Then there exists a positive constant C such that, for any ball B :=x0+Brand t ∈(0, ∞),

Proof of Theorem 2.6By Lemma 3.3, we know that, for any fwith q ∈(q(?), ∞), where q(?) and m(?) are, respectively, as in (2.2) and (2.4), let xi,jdenote the center of Bi,jand ri,jits radius, then there exists a sequence of multiple of(?, q, s)-atoms, {bi,j}i∈Z,j∈N, associated with balls {Bi,j}i∈Z,j∈Nsuch that
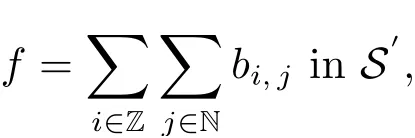

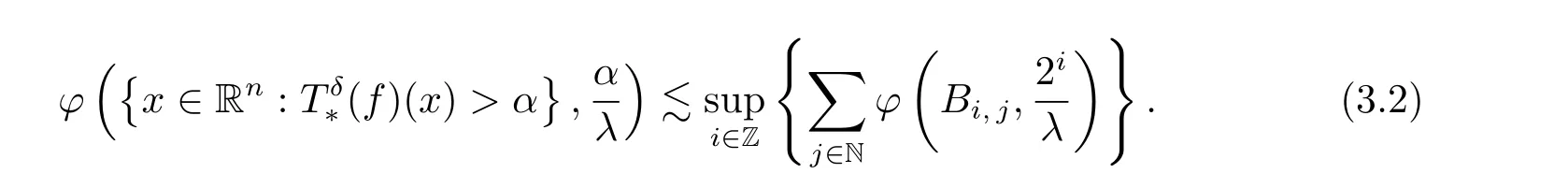
To prove (3.2), we may assume that there exists i0∈Z such that α = 2i0, without loss of generality. Write

Let a ∈(0, 1 ?1/q) be a positive constant, by the well-known weighted Lqboundedness ofwith ? ∈A1?Aq, H?lder’s inequality,for all x ∈Rnand i ∈Z,for i ∈Z and j ∈N, and the uniformly upper type 1 property of ?, we see that
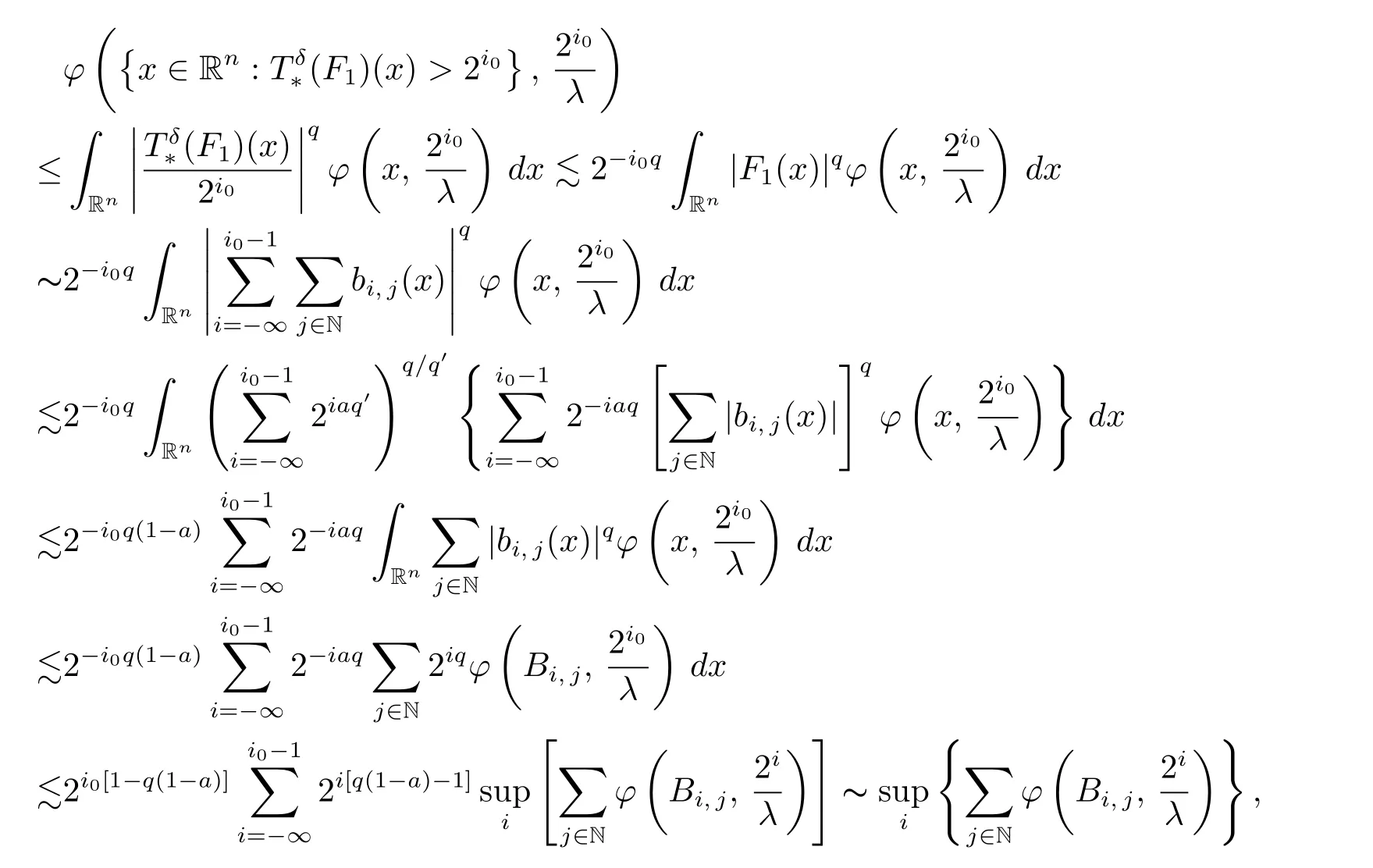
which is wished.
For F2, let xi,jdenote the center of Bi,jand ri,jits radius, and
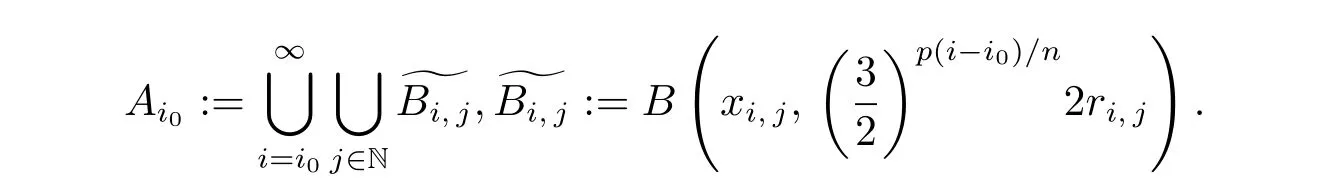
To prove that
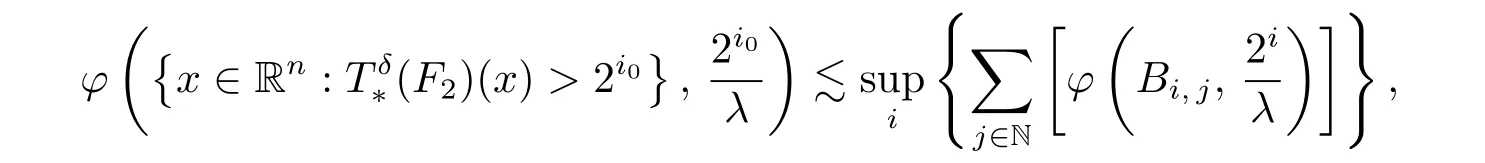
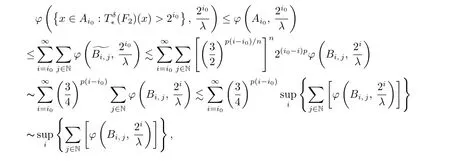
which is also wished.
Let p1:= 2n/(n + 1 + 2δ), since δ > n/p ?(n + 1)/2, we have p1< p. For any(x, t) ∈Rn×(0, ∞), set ?1(x, t) := ?(x, t)tp1?p, then ?1is a Musielak-Orlicz function of uniformly lower type p1and of uniformly upper type 1+p1?p. It is easy to see that
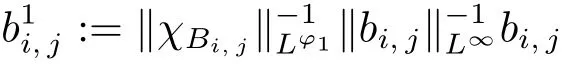
from this, by Lemma 3.6, Lemma 3.4 with ? ∈A1, and the uniformly lower type p property of ?, it follows that

This finishes the proof of Theorem 2.6.

