VECTORIAL EKELAND VARIATIONAL PRINCIPLE AND CYCLICALLY ANTIMONOTONE EQUILIBRIUM PROBLEMS?
Jinghui QIU(丘京輝)
School of Mathematical Sciences,Soochow University,Suzhou 215006,China E-mail:qjhsd@sina.com;jhqiu@suda.edu.cn
Abstract In this article,we extend the cyclic antimonotonicity from scalar bifunctions to vector bifunctions.We find out a cyclically antimonotone vector bifunction can be regarded as a family of cyclically antimonotone scalar bifunctions.Using a pre-order principle(see Qiu,2014),we prove a new version of Ekeland variational principle(brie fly,denoted by EVP),which is quite di ff erent from the previous ones,for the objective function consists of a family of scalar functions.From the new version,we deduce several vectorial EVPs for cyclically antimonotone equilibrium problems,which extend and improve the previous results.By developing the original method proposed by Castellani and Giuli,we deduce a number of existence results(no matter scalar-valued case,or vector-valued case),when the feasible set is a sequentially compact topological space or a countably compact topological space.Finally,we propose a general coercivity condition.Combining the general coercivity condition and the obtained existence results with compactness conditions,we obtain several existence results for equilibrium problems in noncompact settings.
Key words equilibrium problem;cyclic antimonotonicity;vectorial Ekeland variational principle;sequentially compact topological space;countably compact topological space
1 Introduction
In the recent four decades,the famous Ekeland variational principle(brie fly,denoted by EVP;see[12])emerged as one of the most important results of nonlinear analysis due to its signi ficant applications in numerous areas,such as optimization,control theory,game theory,economics, fixed point theory,Banach space geometry,nonlinear equations,dynamical systems,etc.;see,for example[3,10,13,18]and the references therein.Motivated by its wide applications,many authors were interested in the equilibrium versions of EVP and applying them to solve the equilibrium problems,for example,see[1,2,5–7,11,17,22,25,27,30–32,34].The so-called equilibrium problem is a problem of finding∈C such that

where C is a given subset of a space X andis a given bifunction.The pointis called a solution(or,a equilibrium point)of equilibrium problem(1.1).Oettli and Théra[27]started the study of the equilibrium version of EVP and their approach is based on the assumption that the equilibrium bifunction f satis fies the following triangle inequality property
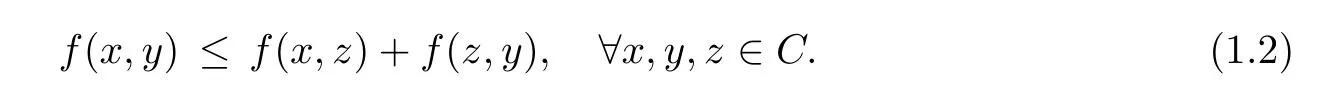
By using the existence of approximate solutions,the authors were able to show the existence of equilibria without any convexity assumption both for the domain and for the function.Subsequently,Bianchi,Kassay and Pini[5]adapted the equilibrium version of EVP to equilibrium problems and showed some existence results for equilibrium problems on general closed sets of Euclidean spaces,or,more generally,of re flexive Banach spaces.They[6]further gave a vectorial equilibrium version of EVP and applied it to vector equilibrium problems de fined on complete metric spaces and with values in locally convex spaces quasi-ordered by closed convex cones.Recently,Alleche and R?dulescu[2]obtained under weakened condition of semicontinuity an existence result for equilibrium problems de fined on weakly compact subsets of Banach spaces.Then,they introduced a weakly compact set of coerciveness rather than closed balls and gave an existence result for equilibrium problems de fined on weakly closed subsets of re flexive Banach spaces,which improves and generalizes the related results in[5,22].As we have seen above,there have been many interesting results on this topics,that is,equilibrium versions of EVP,including vector-valued objective functions and set-valued objective functions,and their applications to equilibrium problems.However,all the previous results are deduced by assuming that the triangle inequality property(1.2)holds,no matter in the scalar-valued,vector-valued,or set-valued case(in the vector-valued and the set-valued case,the inequality≤is de fined by a suitable ordering cone).Very recently,Castellani and Giuli[8]pointed out that(1.2)is indeed a rather strong condition and it is rarely veri fied when the equilibrium problem is a variational inequality.They proposed the concept of cyclic antimonotonicity,which seems to be the natural generalization of the triangle inequality property(1.2).A bifunction f:C×C→R is called cyclically monotone if one has
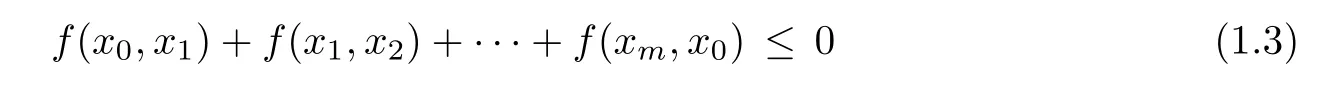
for any m ∈ N and any set of points x0,x1,···,xm∈ C.Under the assumption of cyclic antimonotonicity,they obtained an EVP for equilibrium problems on complete metric spaces,which generalizes several recent results.They also furnished a simple and direct proof of the existence of equilibria for such equilibrium problems in a compact feasible set without passing through the existence of approximate solutions.This fact allows one to remove the metric structure on the topological space and additional technical conditions related to EVP.
The so-called vector equilibrium problem is a problem of finding∈C such that
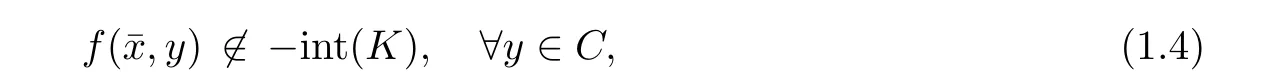
where C is a given subset of a space X,Y is a locally convex space quasi-ordered by a closed convex cone K with intand f:C×C→Y is a given vector bifunction.The pointis called a solution(or,a equilibrium point)of vector equilibrium problem(1.4).To the aim of extending scalar problems to vector problems,several authors provided vector equilibrium versions of EVP,which can be applied to finding approximate solutions of vector equilibrium problems.From the approximate solutions and using some sequential compactness of domains,one can deduce a general existence theorem on solutions of vector equilibrium problems;see,for example,[1,6,30].Furthermore,some authors studied set-valued equilibrium versions of EVP and gave their applications in set-valued equilibrium problems;see,for example[17,31,34].
In this article,we first extend the cyclic antimonotonicity proposed in[8]from scalar bifunctions to vector bifunctions.We shall see that a cyclically antimonotone vector bifunction can be regarded as a family of cyclically antimonotone scalar bifunctions.Using a pre-order principle in[29],we prove a new version of EVP,which is quite di ff erent from the previous ones,for the objective function is a family of scalar functions.From the new version,we deduce several vectorial EVPs for cyclically antimonotone equilibrium problems,which extend the related results in[8].Applying the obtained EVP for cyclically antimonotone vector bifunctions,we give an existence result for vector equilibrium problems,which improves[6,Theorem 3].As pointed out in[8],the existence of solutions of the equilibrium problem for cyclically antimonotone bifunctions is closely linked to the existence of minimums of real functions.Castellani and Giuli[8]gave an original method to show the existence of equilibria when the feasible set is a compact topological space,which only used an elementary result,that is,Weierstrass’theorem.Inspired by Castellani and Giuli’s method,we shall go deep into the problem.We find out that a sequentially lower monotone(strictly weaker than the lower semicontinuity)real function de fined on a sequentially compact topological space is bounded below and attains its minimum.And a lower semicontinuous real function de fined on a countably compact topological space is bounded below and attains its minimum.From the above two elementary facts,we deduce a number of existence results on equilibrium problems for cyclically antimonotone bifunctions(no matter scalar-valued case,or vector-valued case),when the feasible set is a sequentially compact or a countably compact topological space.Thus,we extend and improve the corresponding results in[8].Finally,we study the existence of solutions for equilibrium problems on non-compact feasible sets.We propose a very general coercivity condition.Combining the general coercivity condition with the obtained results on existence for equilibrium problems with compactness condition,we obtain the existence results for equilibrium problems in noncompact setting,which extend and improve some results in[2,5,8,30].
2 Preliminaries
Let X be a nonempty set.As in[15],a binary relationon X is called a pre-order if it satis fies the transitive property(that is,andimply);a quasi order if it satis fies the re flexive(that is,)and transitive properties;a partial order if it satis fies the antisymmetric(that isandimply x=y),re flexive and transitive properties.Letbe a pre-order set.An extended real-valued functionis called monotone with respect to?if for any x1,x2∈X,
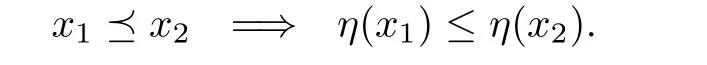
For any given x ∈ X,denote S(x)the set
The following terms and notations on topological vector spaces are the same as in[21,23,24,33].Let Y be a real locally convex Hausdor fftopological vector space(brie fly,denoted by a locally convex space).If A,B ? Y and α ∈ R,the sets A+B and α A are de fined as follows
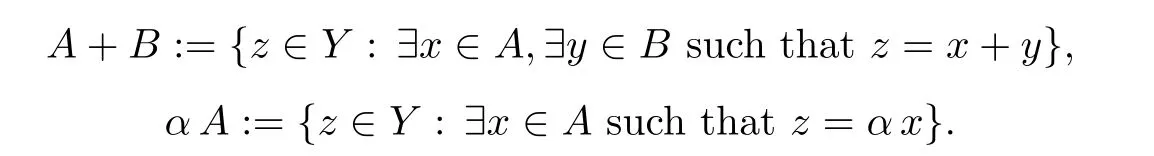
The closure and the interior of A are denoted by cl(A)and int(A),respectively.A nonempty subset K of Y is called cone if α K ? K for any α ≥ 0.And K is called convex cone if K+K ? K and αK ? K for any α ≥ 0.A convex cone K can specify a quasi-order≤Kon Y as follows
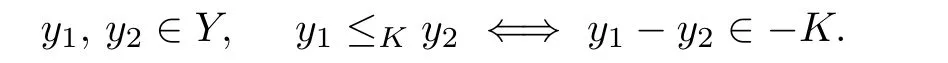
In this case,K is also called the ordering cone or positive cone.We always assume that K is nontrivial,that is,and.Let Y?be the topological dual of Y,that is,a space consisting of all the continuous linear functionals on Y.For any l∈ Y?,we de fine a continuous semi-norm plon Y as follows:The semi-norm family{pl:l∈ Y?}can generate a locally convex Hausdor fftopology on Y(see[21,23,24,33]),which is called the weak topology on Y and denoted by σ(Y,Y?).The positive polar cone of K is denoted by K+,that is,K+={l∈ Y?:l(k)≥ 0,?k∈ K}.For any nonempty subset H of Y,denote the set{l∈Y?:inf{l(h):h∈H}>0}by H+s.It is easy to show thatif and only ifcl(conv(H)+K),where conv(H)denotes the convex hull of H.Particularly,if K is a closed convex cone in Y and k0∈K?K,then.Denote the set{y∈ Y:l(y)≥ 0,?l∈ K+}by K++.If K is a closed convex cone in Y,then K++=K.
De finition 2.1(see[14]) Let X be a topological space and(Y,≤K)be a quasi-ordered locally convex space,where K is a closed convex cone in Y.A vector function ? :X → (Y,≤K)is said to be lower semi-continuous(denoted by lsc)if and only if for any x∈X and any 0-neighborhood V in Y,there exists a neighborhood U of x in X such that ?(U)? ?(x)+V+K;to be quasi-lower semi-continuous(denoted by q-lsc)if and only if for any x∈X and any b∈Y such that,there exists a neighborhood U of x such thatfor each x′∈ U.Obviously,? is q-lsc if and only if for any b∈ Y,the set(? ≤Kb):={x∈ X:?(x)≤Kb}is closed in X.Moreover,? is said to be sequentially quasi-lower semi-continuous(denoted by s-q-lsc)if and only if for any b∈ Y,the set(? ≤Kb)is sequentially closed in X.
De finition 2.2(see[4,19,20]) A vector function ? :X → (Y,≤K)is said to be sequentially lower monotone(denoted by slm)if and only if ?(xn+1)≤K?(xn),?n,and xn→imply that
In[19],slm is called(H4)and in[4],slm is called monotonical semi-continuity.The notions of lsc and q-lsc coincide for real functions.The notions of q-lsc and s-q-lsc coincide when X is a metric space.In general,we haveBut none of the above converses is true;for details,see[9,14,26].Even when X is a compact metric space and Y is the real number space endowed with the usual order(in this case,we still have slm
Example 2.3(refer to[9]) Let X=[?1,1]? R be endowed with the usual topology and Y=R be endowed with the usual order.Let ? :X →Y be de fined as follows
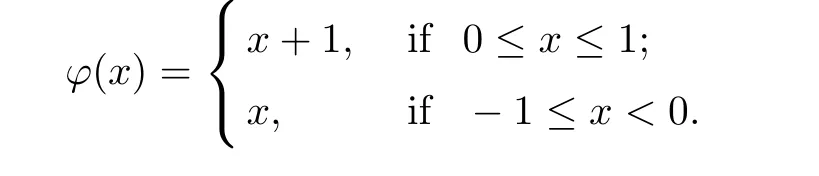
It is easy to veryfy that ? is slm.But it is not lsc since the set{x ∈ X:?(x)≤ 1/2}=[?1,0)is not closed in X.
For vector bifunctions,we also have the notion of slm.
De finition 2.4(see[30]) A vector bifunction f:X×X →(Y,≤K)is said to be sequentially lower monotone(denoted by slm)if and only if f(xn,xn+1)≤K0,?n,andimply that
It is easy to show that if for each x ∈ X,the functionis s-q-lsc(or q-lsc,or lsc)and the triangle inequality property(1.2)is satis fied,then f is slm.But the converse is not true(for details,see[30,Remark 2.6(ii)]).
At the end of this section,we further recall the notion of upper semi-continuity.
De finition 2.5(see[17]) Let X be a topological space and(Y,≤K)be a quasi-ordered locally convex space,where K is a closed convex cone in Y.A vector function ? :X → (Y,≤K)is said to be upper semi-continuous(denoted by usc)if and only if for any x∈X and any 0-neighborhood V in Y,there exists a neighborhood U of x in X such that ?(U)? ?(x)+V ?K.
By the basic theory of topological vector spaces,we may assume that V satis fies V=?V.Thus,comparing De finitions 2.1 and 2.5,we have the following.
Proposition 2.6(see[31,Remark 2.3]) A vector function ? :X → (Y,≤K)is usc if and only if?? is lsc.
Proposition 2.7If ? :X → (Y,≤K)is usc,then for any l∈ K+{0},l?? :X → R is usc.
ProofTake any α ∈ R and l∈ K+{0}.Let x0∈ {x ∈ X:l??(x)< α}.Take ? such that
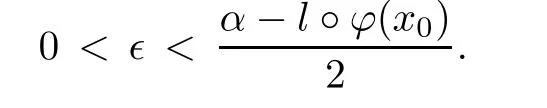
Put V:={y ∈ Y:|l(y)|< ?}.Then V is a 0-neighborhood in Y.Since ? is upper semicontinuous at x0,there exists a neighborhood U(x0)of x0such that
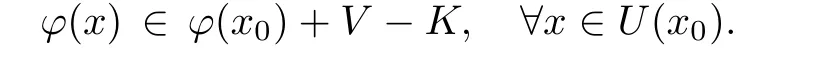
Hence
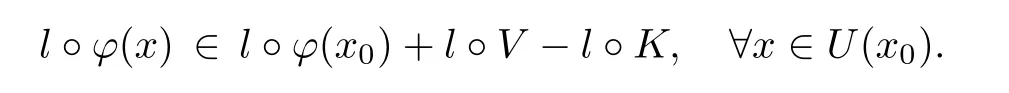
Thus,for any x∈U(x0),there exists v∈V such that
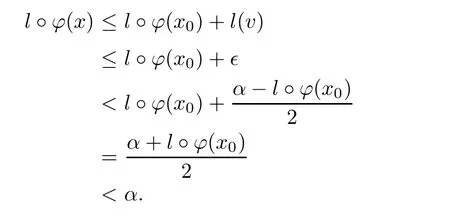
From this,we know that the setis an open set and l?? is upper semi-continuous. ?
3 Ekeland Variational Principle for Cyclically Antimonotone Vector Bifunctions
In this section,we shall extend the cyclic antimonotonicity(see[8])from scalar bifunctions to vector bifunctions and establish several versions of EVP for cyclically antimonotone vector equilibrium problems.
De finition 3.1Let C be a nonempty set and Y be a locally convex space quasi-ordered by a closed convex cone K.A vector bifunction f:C×C→Y is said to be cyclically antimonotone if and only if f(x0,x1)+f(x1,x2)+ ···+f(xm,x0)≥K0 for any m ∈ N and any x0,x1,···,xm∈ C.
Lemma 3.2A vector bifunction f:C×C→Y is cyclically antimonotone if and only if for everyis cyclically antimonotone.
ProofAssume that f is cyclically antimonotone.Then,for any m ∈ N,any x0,x1,···,xm∈C,

Thus,for any l∈K+,we have
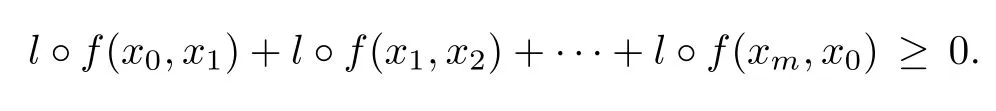
That is,l?f is cyclically antimonotone.
Conversely,assume that for every l∈ K+,l?f is cyclically antimonotone.Then,for any m ∈ N and any x0,x1,···,xm∈ C,
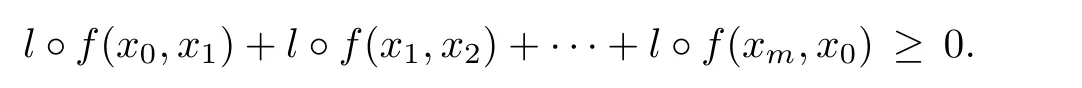
From this,we know that
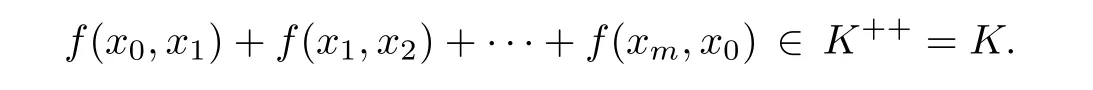
That is,f is cyclically antimonotone.?
The proof of the following lemma is exactly the same as the proof of[8,Theorem 2.13].
Lemma 3.3A vector bifunction f:C×C→Y is cyclically antimonotone if and only if for any l∈ K+,there exists ?l:C → R such that
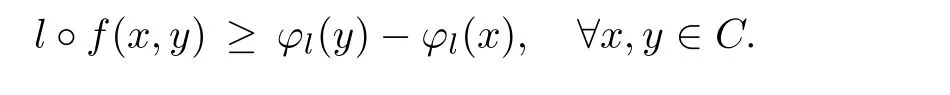
As we have seen,a cyclically antimonotone vector bifunction f can be regarded as a family of cyclically antimonotone scalar bifunctionsFirst,we give an EVP,whose version is quite di ff erent from the previous ones for the objective function is a family of real functions.
Theorem 3.4Let(X,d)be a complete metric space,Y be a locally convex space quasiordered by a closed convex cone K and k0∈ K? K.Letbe a family of real functions which are slm.Suppose that there exists l0∈ K+∩ {k0}+ssuch that ?l0is bounded below on X.Then,for any x0∈X,there existssuch that
In order to give the proof of Theorem 3.4,we need the following pre-order principle.
Suppose that the following conditions are satis fied:
(B)For any x ∈ S(x0)with ?∞ < η(x)<+∞ and x′∈ S(x){x},one has η(x)> η(x′).
(C)For any sequence(xn)? S(x0)with xn∈ S(xn?1), ?n,such that η(xn)?inf{η(x):x∈S(xn?1)}→0(n→∞),there exists u∈X such that u∈S(xn),?n.
Proof of Theorem 3.4For any x,x′∈ X,de fineif and only if
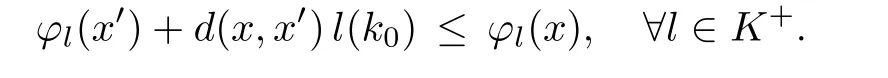
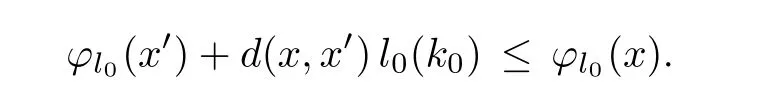
Obviously,
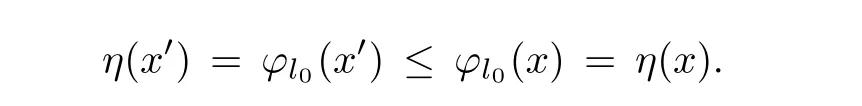
So,η is monotone with respect to?.Next,we show that conditions(A),(B)and(C)in[29,Theorem 2.1]are satis fied.
Prove that(A)is satis fiedThat is,?∞ Thus, On the other hand,by the assumption,?l0is bounded below on X.Thus, Combining(3.1)and(3.2),we have?∞ Prove that(B)is satis fiedThat is,for any x∈S(x0)with?∞ < η(x)<+∞ and x′∈ S(x){x},one has η(x)> η(x′).Obviously,for any x ∈ S(x0),we have η(x)= ?l0(x) ∈R.By x′∈ S(x),we have Particularly, Prove that(C)is satis fiedLet a sequence(xn)? S(x0)such that xn∈ S(xn?1),?n,and such that We shall show that there exists u∈X such that u∈S(xn),?n.Since xn+1∈S(xn)and sincesatis fies the transitive property,we have xn+p∈ S(xn+p?1)? ···? S(xn), ?n,?p.Thus, Particularly, Thus(xn)is a Cauchy sequence in(X,d).Since(X,d)is complete,there exists u∈X such that xn→ u(n→ ∞).By(3.3)and ?lbeing slm,we have Let n be given and let p→∞,we have This means that u∈S(xn),?n. Now,we can apply[29,Theorem 2.1]and conclude that there existssuch thatand.Clearly,means that(a)holds.Also,leads to that for anywhich means thatsuch thatThat is,(b)holds.? From Theorem 3.4 we can deduce the following vectorial EVP for cyclically antimonotone equilibrium problems. Theorem 3.5Let C be a nonempty closed subset of a complete metric space(X,d),Y be a locally convex space quasi-ordered by a closed convex cone K and k0∈K?K.Let f:C×C→Y be cyclically antimonotone,that is(see Lemma 3.3),for each l∈K+,there exists a real function ?l:C → R such that Suppose that every ?lis slm and there existssuch that ?l0is bounded below on C. Then,for any x0∈C,there exists∈C such that ProofSince C is a closed subset of a complete metric space,(C,d)is also a complete metric space.Replacing(X,d)by(C,d)in Theorem 3.4,we know that for any x0∈C,there exists∈C such that and Obviously,(3.5)is just(a)we need to prove.Next we show that(3.6)implies that(b)holds.If not,there exists x′∈C{}such thatThen,for every l∈K+, Also, By(3.7)and(3.8),we have This contradicts(3.6). Theorem 3.6Let(X,d)be a complete metric space,Y be a locally convex space quasiordered by a closed convex cone K and k0∈K?K.Suppose that ?:X →Y is a slm vector function and there exists l∈K+∩{k0}+ssuch that l??(X)is bounded below. Then,for any x0∈X,there exists∈X such that ProofFor any x,x′∈ X,de fineif and only if Hence Thus So η is monotone with respect toFor x0∈ X,putAs done in the proof of Theorem 3.4,we can show that conditions(A),(B)and(C)in[29,Theorem 2.1]are satis fied.Applying[29,Theorem 2.1],we conclude that there existssuch thatandThis implies that(a)and(b)hold.? Theorem 3.7Let C be a nonempty closed subset of a complete metric space(X,d),Y be a locally convex space quasi-ordered by a closed convex cone K and k0∈K?K.Let f:C×C→Y be a vector bifunction.Suppose that the following conditions are satis fied (i)f is a strongly cyclically antimonotone bifunction,that is,there exists ?:C → Y such that (iii)? is slm. Then,for any ?>0 and any x0∈C,there existssuch that ProofSince C is closed in(X,d)and(X,d)is complete,we may consider a complete metric space(C,d)instead of(X,d)(for convenience,we disregard ?).By Theorem 3.6,there existssuch that and Clearly,(3.9)is just(a)we need to prove.From(3.10)and condition(i):f(x,y)≥K?(y)??(x),?x,y∈ C,we easily deduce that Remark 3.8Here we introduce a new notion:strong cyclic antimonotonicity.Obviously,a vector bifunction f:C×C→(Y,≤K)being strongly cyclically antimonotone implies that f is cyclically antimonotone.But we don’t know whether the converse is true.Clearly,Theorems 3.5 and 3.7 can be regarded as two versions of vector-valued generalizations of[8,Theorem 2.4]. Inspired by[8,Theorem 2.20],we give a vector version of Ekeland’s principle for quasiequilibrium problems. Theorem 3.9Let C be a nonempty closed subset of a complete metric space(X,d),be a set-valued map,Y be a locally convex space quasi-ordered by a closed convex cone K and k0∈K?K.Let f:C×C→Y be a vector bifunction satisfying the following conditions: (i)there exists ?:C → Y such that (ii)there exists l∈K+∩{k0}+ssuch that l??(C)is bounded below; (iii)? is slm. Then,for any ?>0 and any x0∈ C such that the following implication holds ProofClearly,(C,d)is also a complete metric space.Replacing(X,d)by(C,d)in Theorem 3.6,there existssuch that(a)holds and such that Thus,(b)holds. From[8],we know that a bifunction f:C×C→R is cyclically antimonotone if and only if there exists a function ?:C → R such that Thus,when the objective equilibrium function f is cyclically antimonotone,the equilibrium problem(1.1)may be reduced to a minimum problem of ?.Since the minimum problem of real functions is often linked to some compactness of the domains,we recall three kinds of compactness.A topological space is compact if and only if each cover by open sets has a finite subcover if and only if each net has a cluster point.A space is countably compact if and only if each countable cover by open sets has a finite subcover if and only if each sequence has a cluster point.A space is sequentially compact if and only if each sequence has a subsequence which converges to a point in the space(see[23,24]).Although countable compactness is implied by the two other kinds of compactness,it implies neither of these,nor does either of these imply the other. In this section,inspired by the original method proposed in[8],we shall go deep in the problem and obtain several more precise results.For a real function ? :C → R,if C is a sequentially compact topological space,then we only require ? is slm(instead of lsc)in order that ? attains its minimum. Theorem 4.1Let C be a sequentially compact topological space and let ? :C → R be slm.Then,? attains its minimum on C. ProofFirst,we prove that ? is bounded below on C.If not,assume that ? is not bounded below on C.Then,Thus,there exists x1∈C such that ?(x1)≤ ?1.Also,{x ∈ C:?(x)≤ ?(x1)?1}Thus,there exists x2∈ C such that ?(x2)≤?(x1)?1≤?2.In general,if xn∈C is given such that ?(xn)≤ ?(xn?1)?1 ≤ ?n,then{x ∈ C:?(x)≤ ?(xn)?1}Thus,there exists xn+1∈ C such that ?(xn+1)≤?(xn)?1≤ ?(n+1).Repeating this process in finitely,we obtain a sequence(xn)? C.Since C is sequentially compact,there exists a subsequence(xni)of(xn)andsuch thatSince ?ni+1≤?(xni)and ? is slm,we havefor all i.This leads to,which contradicts ?(x)∈R for all x. Now,we may assume m:=inf{?(x):x∈C}> ?∞.Since C is a sequentially compact topological space,as shown in the proof of[9,Proposition 1.4],we conclude that there existssuch that? Theorem 4.2Let C be a sequentially compact topological space and let f:C×C→R be a cyclically antimonotone bifunction such that there exists a slm function ? :C → R satisfying ProofBy Theorem 4.1,there existssuch that,?y∈C.Thus, Though three kinds of compactness are di ff erent,but in the weak topology of a normed space(more generally,in the weak topology of a metrizable locally convex space),the three kinds of compactness coincide.That is,a subset A of the normed space is weakly sequentially compact if and only if it is weakly compact if and only if it is weakly countably compact(see[24,33]).So,by Theorem 4.2,we have the following corollary. Corollary 4.3Let C be a weakly countably compact subset of the normed space(or,of the metrizable locally convex space)X and let f:C×C→R be a bifunction such that there exists a function ? :C → R satisfying where ? is slm with respect to the weak topology.Then,there exists∈C such that When ? :C → R is lsc(which is stronger than slm),then the compactness condition on C can be weakened.Here,we only need to require that C is countably compact for ? attaining its minimum. Theorem 4.4Let C be a countably compact topological space and let ? :C → R be lsc.Then,? attains its minimum on C ProofFirst,we prove that ? is bounded below on C.Assume the contrary.For any n∈N,the set.Since ?:C →R is lsc,we know that everyCnis a nonempty closed set.Remarking that C is countably compact,we have Thus,there existsand hencefor every n.This contradicts Now,we may assume that m:=inf{?(x):x∈ C}> ?∞.We shall prove that there existssuch that.Take any x1∈C.If ?(x1)=m,then we may takeand the result holds.If not,?(x1)>m,then we may take x2∈C such that As done above,we only need to consider the case that ?(x2)>m.Thus,we may take x3∈ C such that Repeating the above process successively,we can prove the result according to the following two cases. Case 1There exists n∈N such that ?(xn)=m.In this case we may take. Case 2For every n∈N,.Thus,we obtain a decreasing sequence of nonempty closed sets(Dn),where Using Theorem 4.4,we can directly obtain the following result. Theorem 4.5Let C be a countably compact topological space and let f:C×C→R be a cyclically antimonotone bifunction such that there exists a lsc function ? :C →R satisfying If f:C×C→R is a cyclically antimonotone bifunction such that for eachis upper semicontinuous,then by[8,Theorem 2.16]we know that there exists a lsc function ? :C → R such that f(x,y)≥ ?(y)??(x),?x,y∈ C.Now,applying Theorem 4.5,we obtain the following result. Theorem 4.6Let C be a countably compact topological space and let f:C×C→R be a cyclically antimonotone bifunction such that for eachis upper semicontinuous.Then,there existssuch that First,by using an EVP for cyclically antimonotone vector bifunctions,we give an existence result for vector equilibrium problems. Theorem 4.7Let(C,d)be a compact metric space,Y be a locally convex space quasiordered by a closed convex cone K.Suppose that the vector bifunction f:C×C→Y satis fies the following conditions: (i)f is cyclically antimonotone; ProofBy(i),for each l∈ K+,l?f is cyclically antimonotone(see Lemma 3.2).By(ii),for each y ∈ C and each l∈ K+,the functionis upper semi-continuous(see Proposition 2.7).By[8,Theorem 2.16],for each l∈ K+,there exists a lsc function ?l:C → R such that Take any k0∈K?K.Since K is closed,by the separation theorem,there exists l0∈K+∩{k0}+s.Now,?l0is lsc and C is a compact metric space,applying Theorem 4.4 we conclude that ?l0is bounded below on C.By Theorem 3.5,for each n∈N,there existssuch that Since(C,d)is a compact metric space(which is also sequentially compact),there exists a subsequenceofand a pointsuch thatin(C,d).We assert that By(ii),there exists a neighborhoodofsuch that Take nilarge enough such thatand Combining(4.4),(4.3)and(4.2),we have which contradicts(4.1). Remark 4.8Let us compare our Theorem 4.7 with[6,Theorem 3].For reader’s convenience we recall the result. Theorem 3 in[6].Let(X,d)be a compact metric space.Assume that the function f:X×X→Y satis fies the following conditions: (i)f(t,t)=0 for all t∈X; (iii)f(z,y)+f(y,x)∈f(z,x)+K for any x,y,z∈X; As we saw in[8],the above conditions(i)and(iii)in[6,Theorem 3]imply that f is cyclically antimonotone;but the converse is not true.Besides,conditions(ii)and(iv)in[6,Theorem 3]were removed. Next,we shall apply the obtained results in Subsection 4.1 to study the existence of solutions for vector equilibrium problems.In particular,from Theorem 4.1 we can deduce the following. Theorem 4.9Let C be a sequentially compact topological space,Y be a locally convex space quasi-ordered by a closed convex cone K and let f:C×C→Y be a vector bifunction. Suppose that there exists l∈ K+{0}and a slm function ?l:C → R such that ProofSince C is sequentially compact and ?l:C → R is slm,by Theorem 4.1 we know that ?lis bounded below on C and attains its minimum on C.That is,there existssuch thatBy(4.5),we have Now,we assert that the result holds.If not,there existssuch that?int(K).Since l∈K+{0},we conclude that,which contradicts(4.6).? Similarly,from Theorem 4.4 we can deduce the following. Theorem 4.10Let C be a countably compact topological space,Y be a locally convex space quasi-ordered by a closed convex cone K and f:C×C→Y be a vector bifunction. Suppose that there exists l∈ K+{0}and a lsc function ?l:C → R such that ProofSince C is countably compact and ?l:C → R is lsc,by Theorem 4.4 we know that ?lis bounded below on C and attains its minimum on C.That is,there existssuch that,?y∈C.Thus, As done in the proof of Theorem 4.9,we have Theorem 4.11Let C,Y,K and f:C×C→Y be the same as in Theorem 4.10.Suppose that there exists l∈K+{0}such that (i)l?f is cyclically antimonotone; (ii)for each y ∈ C,the functionis upper semi-continuous.Then there existssuch that ProofSince l?f is cyclically antimonotone and since for eachis upper semi-continuous,by[8,Theorem 2.16]we conclude that there exists a lsc function ?l:C→R such that Now,applying Theorem 4.10 we obtain the result. From Theorem 4.11,we easily deduce the following result. Theorem 4.12Let C,Y,K and f:C×C→Y be the same as in Theorem 4.10.Suppose that f satis fies the following conditions (i)f is cyclically antimonotone; As we have seen,here the feasible set C is just a topological space:the metric is not required.Obviously,Theorems 4.11 and 4.12 improve[6,Theorem 3]. In order to obtain existence results for vector equilibrium problems in non-compact settings,we need to require some more conditions.In this section,we always assume that(X,T)is a topological space,Y is a locally convex space,K?Y is a closed convex cone and f:X×X→Y is a vector bifunction.We consider the vector equilibrium problem,that is,to findsuch that where(X,T)is non-compact. Theorem 5.1Let f:X×X→Y satisfy:there exists l∈K+{0}such that (i)l?f is cyclically antimonotone; (ii)there exists a lsc function ? :(X,T)→ R such that Moreover,assume that the following conditions are satis fied: (A1)there exists a function p:X ×X → R and a Hausdor fftopology τ on X(possibly di ff erent from the initial topology T)such that for any x∈ X and any r>0,the set{x′∈ X:p(x′,x) ≤ r}is τ-compact; (A2)for any x ∈ X,the set{y∈ X:?(y)≤ ?(x)}is τ-closed; (X(a))there exists a countably compact subset C of X and a point a∈X such that for any x∈XC,there exists y∈X satisfying Then,there exists xC∈X such that ProofSince ? is lsc and C is countably compact with respect to T,by Theorem 4.4 there exists xC∈C such that Next,we show that Assume the contrary.There existssuch thatBy(5.1),we know thatBy(X(a)),there existssuch that Put Corollary 5.2Let f:X×X→Y satisfy:there exists l∈K+{0}such that (i)l?f is cyclically antimonotone; Moreover,assume that(A1),(A2)and(X(a))in Theorem 5.1 are satis fied. Then the result in Theorem 5.1 holds. ProofBy(i)and(ii),and using[8,Theorem 2.16],we conclude that there exists a lsc function ? :X →R such that Now,we can apply Theorem 5.1 and obtain the result. Obviously,conditions(i)and(ii)in Corollary 5.2 can be replaced by the following stronger conditions: (i)′f is cyclically antimonotone; (ii)′for eachis upper semi-continuous. As we have seen in Section 2,for real functions,the notions of lsc and q-lsc coincide.Hower,the notions of lsc and s-lsc(that is,sequential lower semi-continuity)don’t coincide when the domain space is non-metrizable.In general,lscs-lsc;but the converse is not true.For example,Let X be a locally convex space which isn’t a Mazur space.For the existence of such a space,please refer to[33,prob.10-4-301]or[28,Example 3.2].Thus,there exists a sequentially continuous linear functional ? on X which is not continuous.It is easy to show that for a linear functional on a locally convex space,the lower semicontinuity is equivalent to continuity.Hence,? is s-lsc but not lsc.Similarly,we also have the notion of sequential upper semi-continuity(denoted by s-usc).It is easy to show that a function ? is s-lsc if and only if?? is s-usc. The following result is a vector extension of[8,Theorem 3.8]. Theorem 5.3Let(Z,k·k)be a re flexive Banach space,X ? Z be a nonempty weakly closed set,Y be a locally convex space,K?Y be a closed convex cone.Let f:X×X→Y satisfy:there exists l∈K+{0}such that (i)l?f is cyclically antimonotone; (ii)there exists a weakly sequentially lower semi-continuous(denoted by s-lsc)function ?:X→R such that Moreover,assume that the following condition is satis fied (X(0))there exists a weakly compact subset C of X such that for any x∈XC,there exists y∈X satisfying Then there exists xC∈X such that ProofSinceis a normed space,the weakly compact set C is also a weakly sequentially compact set.Also,? is weakly s-lsc.By Theorem 4.1,we know that there exists xC∈C such that Next,we show that Put Since(Z,k·k)is a re flexive Banach space and X ? Z is a weakly closed set,we know thatis weakly compact,equivalently,it is weakly sequentially compact.On the other hand,? is weakly s-lsc,so the setis weakly sequentially closed.Hence, is weakly sequentially compact.Since the normis weakly lsc,there existssuch that Thus,y0∈S(x0)?S()and a contradiction!Thus,we have shown that(5.4)holds.This leads to If there exists y′∈ X such that f(xC,y′) ∈ ?int(K),then l?f(xC,y′)<0,which contradicts(5.5). ? From Theorem 5.3 we can deduce the following corollary,which extends and improves[2,Theorem 3.2]and[5,Theorem 4.1]. Corollary 5.4In Theorem 5.3,the result remains true if condition(ii)is replaced by the following condition (ii)′for eachweakly sequentially upper semi-continuous(denoted by s-usc). ProofAs pointed out in[8,Theorem 2.13],from(ii)′we can deduce that there exists a weakly s-lsc function ? such that Thus,applying Theorem 5.3,we conclude that the result holds. Finally,we shall give an improvement of[30,Corollary 4.8].We recall(see[16,p.30])that a Hausdor fftopological space X is called angelic if for any relatively countably compact set A?X,the following holds: (a)A is relatively compact; (b)for each x∈cl(A),there is a sequence(xn)?A such that xn→x. In angelic space,the following statements of the?mulian theorem hold Also,we recall(see[33,Chapter 15])that a Banach space(E,k·k)is called a weakly compact generated(denoted by WCG)space if there exists a weakly compact subset C such that E=cl(span[C]),where span[C]denotes the smallest linear subspace containing C.Obviously,a re flexive or separable Banach space is a WCG space;but there are WCG spaces which are neither separable nor re flexive(see[33]). Lemma 5.5(see[16,Section 3.10]or[30,Lemma 4.7]) Let(E,k·k)be a WCG space.Then,(E?,σ(E?,E))is angelic and the following holds:for any subset A ? E?,σ(E?,E)-compact-countably compactσ(E?,E)-sequentially compact. Theorem 5.6Let(E,k ·k1)be a WCG space andbe its strong dual.Letand X ? Z be a nonempty σ(E?,E)-closed set endowed with the topology τ induced by σ(E?,E).Let Y be a locally convex space quasi-ordered by a closed convex cone K.Let f:X×X →Y satisfy:such that (i)l?f is cyclically antimonotone; (X(0))there exists a σ(E?,E)-compact set C such that for any x ∈ XC,there exists y ∈ X such that kyk ProofBy(i)and(ii)and using[8,Theorems 2.13 and 2.16],we conclude that there exists a s-lsc function ? :X →R such that By Lemma 5.5,C is also sequentially compact with respect to τ.Applying Theorem 4.9,we conclude that there exists xC∈C such that Next,we show that Put By Alaoglu-Bourbaki theorem(see[24,33]),the setis σ(E?,E)-compact.By Lemma 5.5,it is also σ(E?,E)-sequentially compact.Since ? is s-lsc,the setis σ(E?,E)-sequentially closed.Thus,L(),as the intersection of the above two sets,is σ(E?,E)-sequentially compact.Noting that the functionis lower semi-continuous with respect to σ(E?,E),we conclude that there existssuch that k?k=min{kyk:y∈L()}.We show the result according to the following two cases. Case 1LetThen,by(5.8)we havewhich contradicts(5.6). Case 2LetThen,by(X(0)),there exists y1∈X such that a contradiction!Thus,we have shown(5.7).From this,we conclude that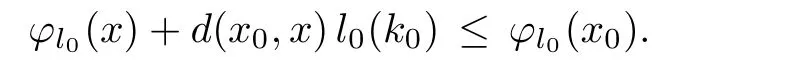
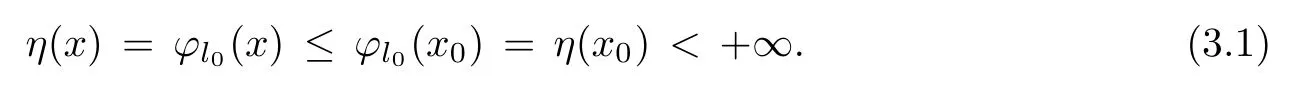
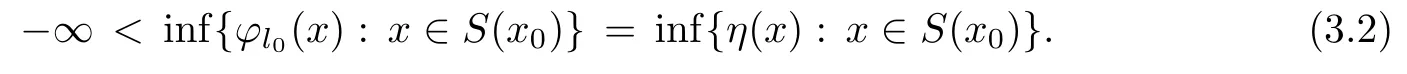
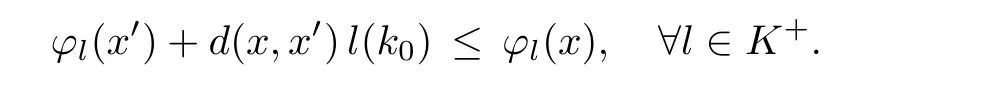
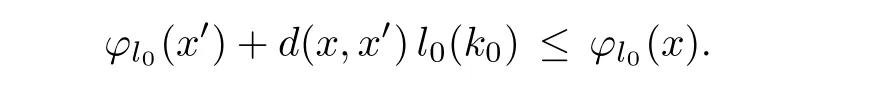
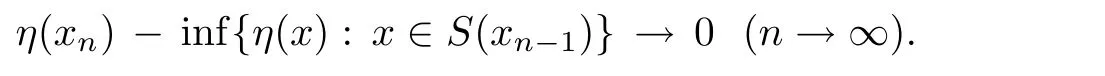
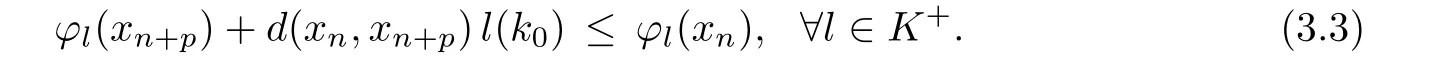
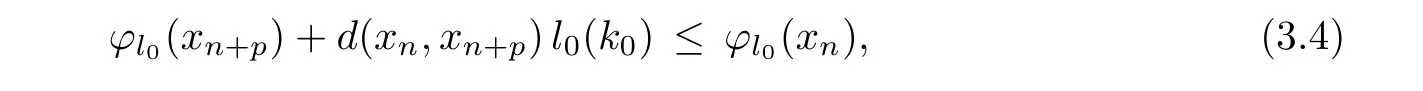
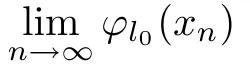
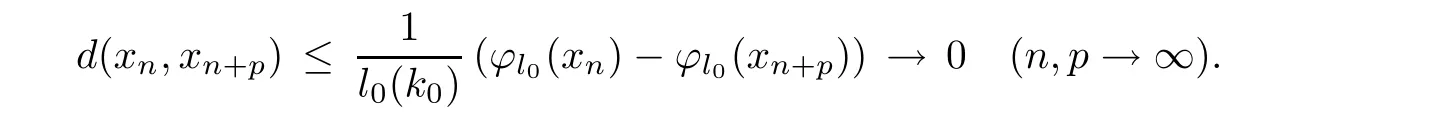
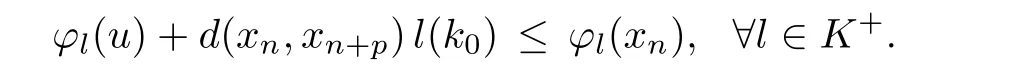
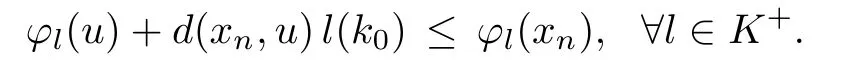
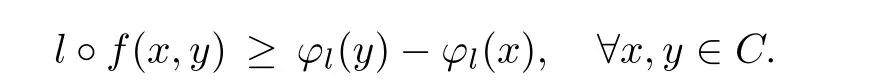

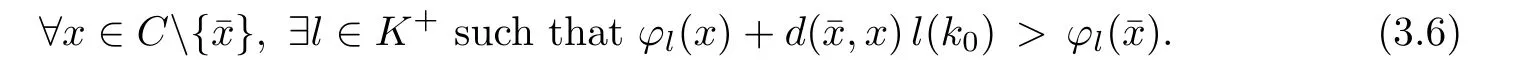
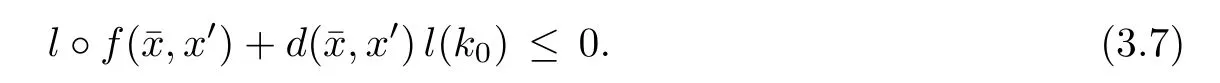
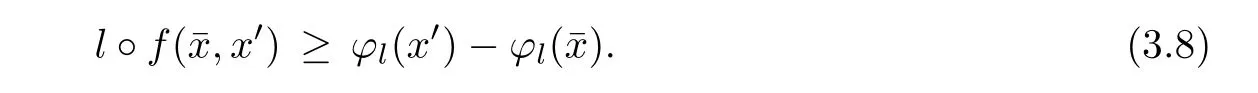
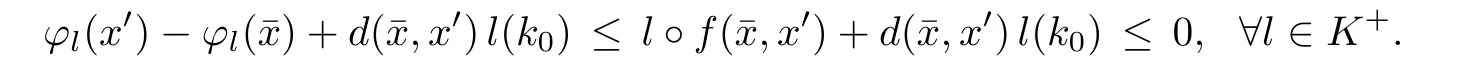
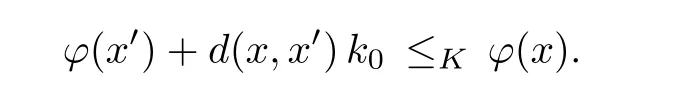

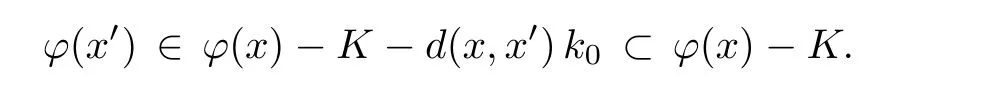
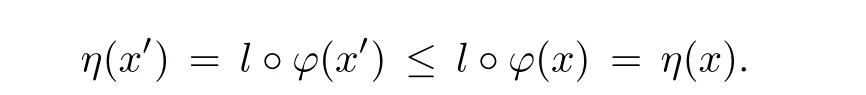
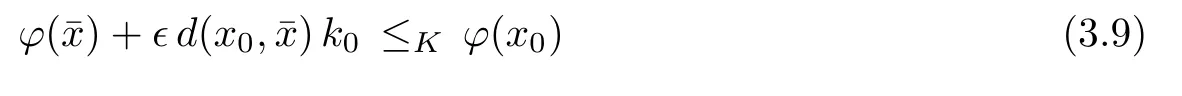
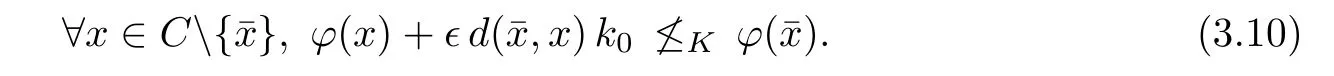
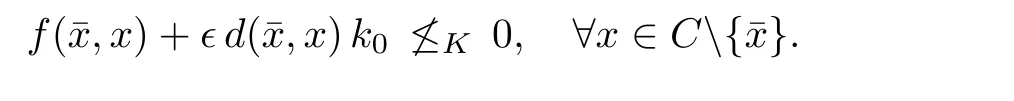
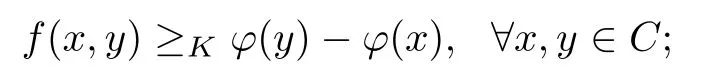
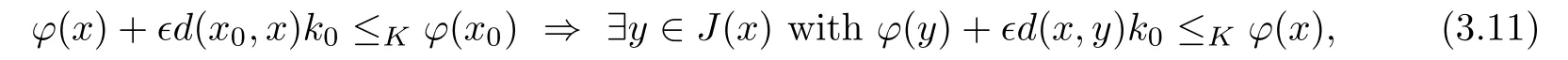
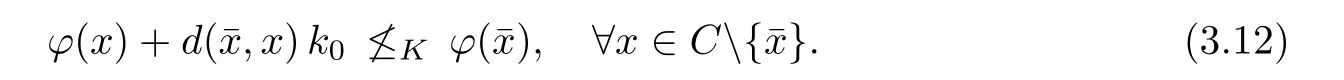
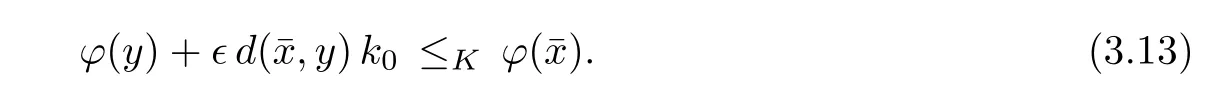
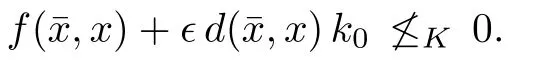
4 Cyclically Antimonotone Equilibrium Problems
4.1 Existence Results for Scalar Equilibrium Problems
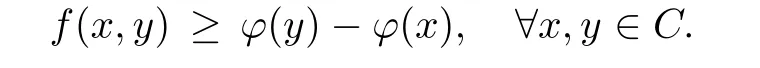
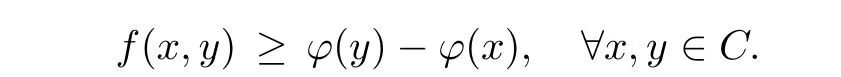

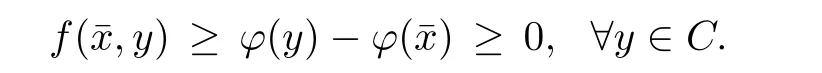
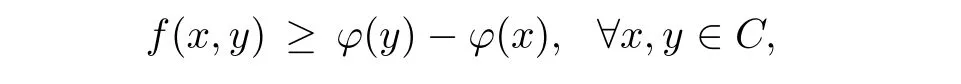
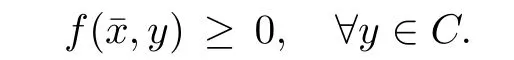
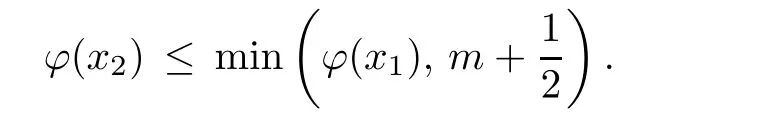
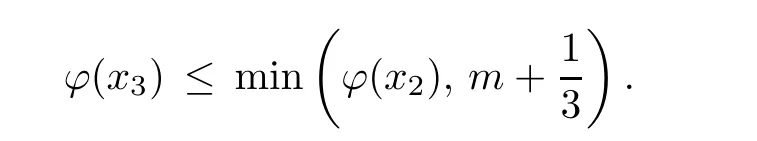
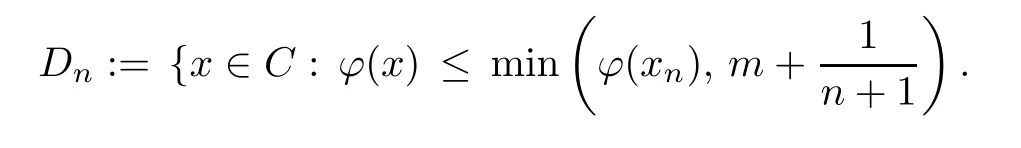
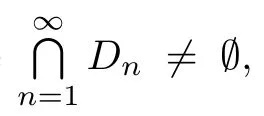
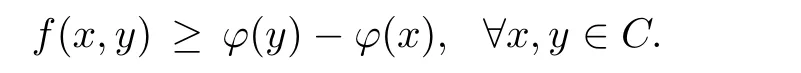
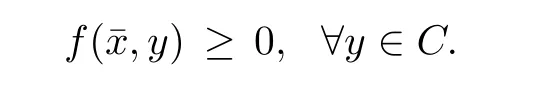
4.2 Existence Results for Vector Equilibrium Problems
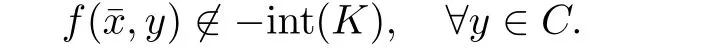
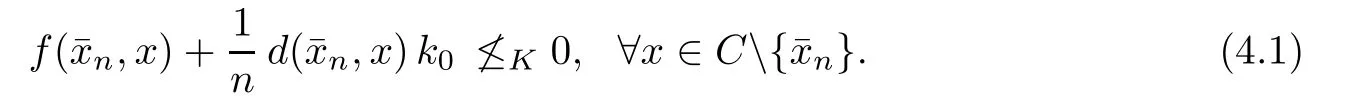
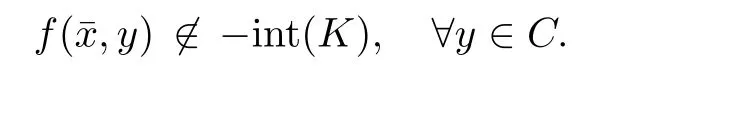
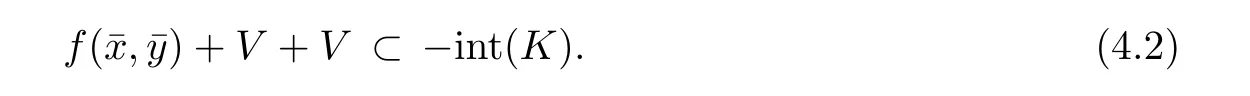
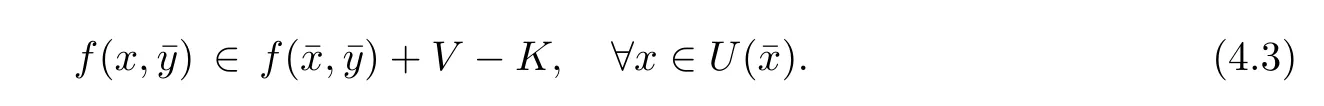

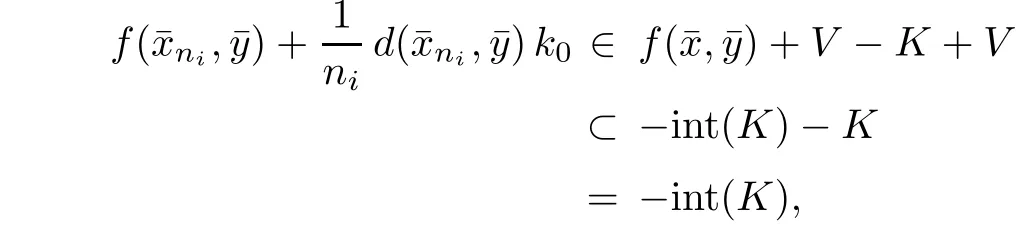
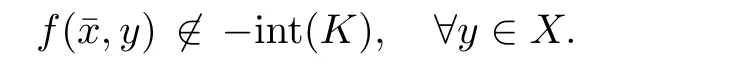
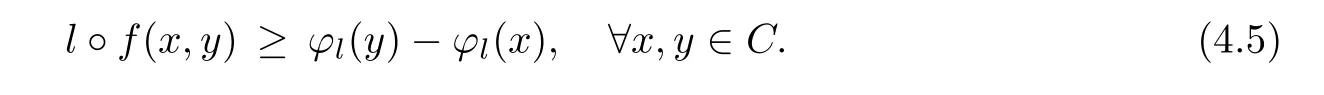
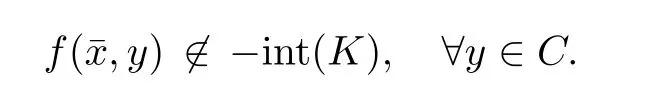
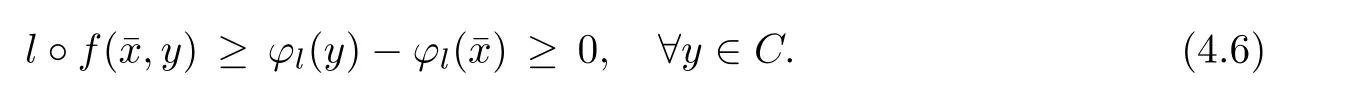
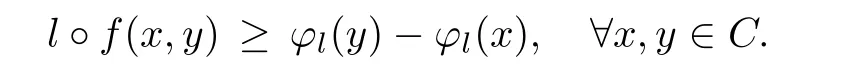
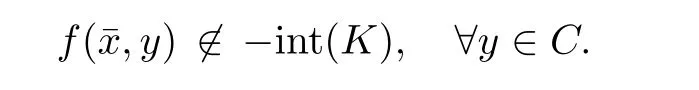
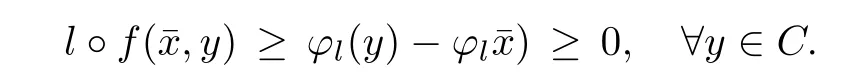
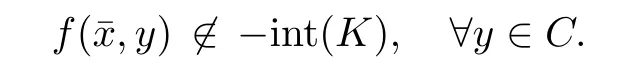
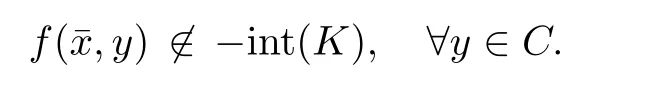
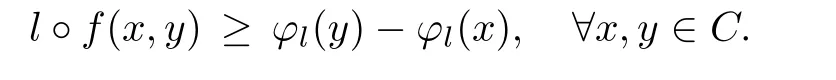
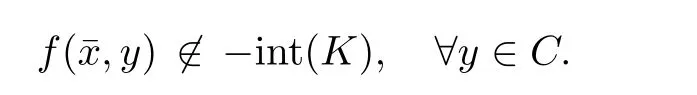
5 Vector Equilibrium Problems with Non-Compact Feasible Sets
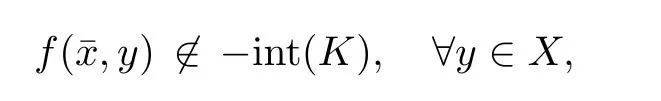
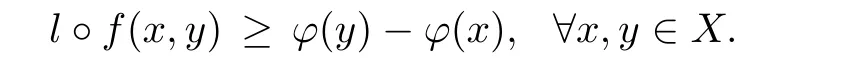





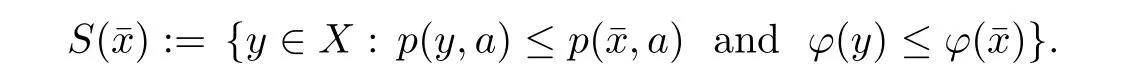
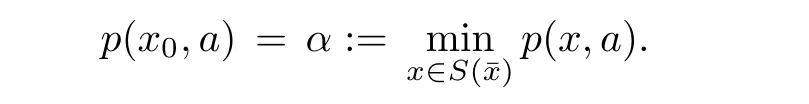

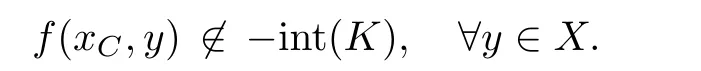
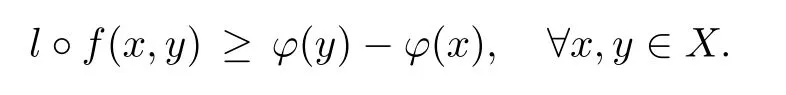

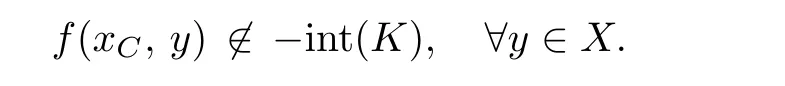


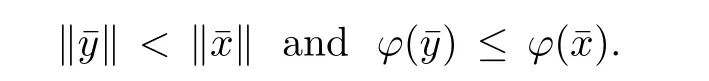
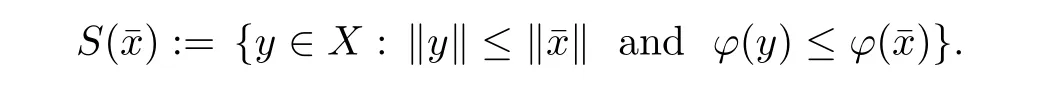
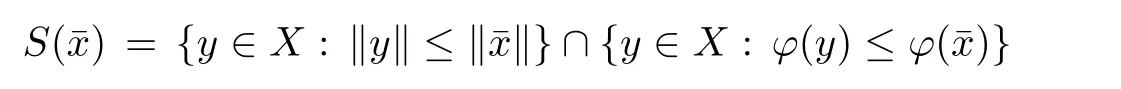
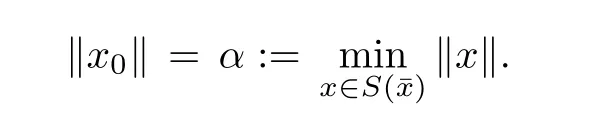
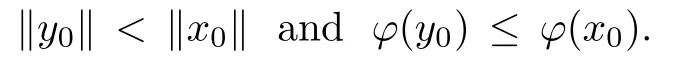
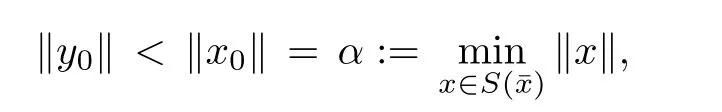
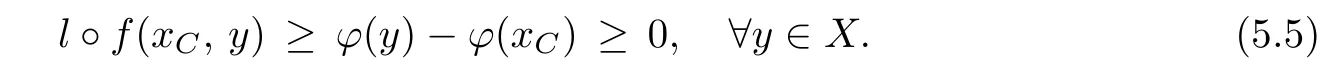
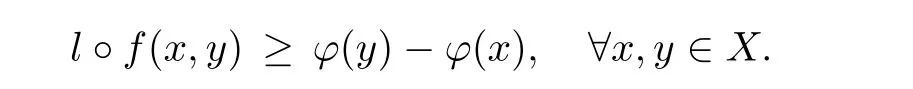
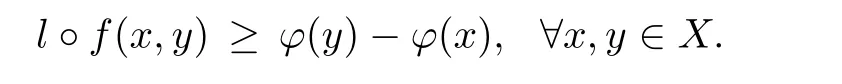



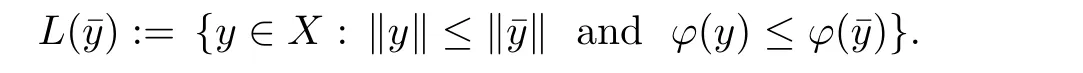
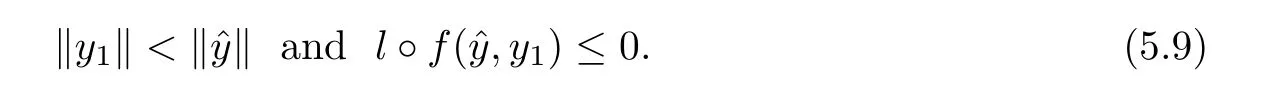
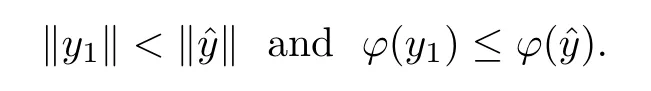
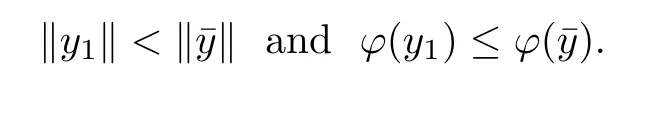
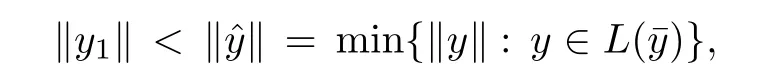

 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
