民機系統部件維修間隔優(yōu)化

李景奎,藺瑞管,段飛飛,王俊輝

(1.沈陽航空航天大學 民用航空學院,沈陽 110136; 2.中國南方航空股份有限公司 沈陽維修基地,沈陽 110136)

隨著民航業(yè)的快速發(fā)展,航空公司的飛機維修需求大幅上升,飛機維修成本已經成為民航企業(yè)運營成本的重要組成部分,降低維修成本成為企業(yè)盈利的關鍵,而維修費用的高低與民機系統維修規(guī)劃是否合理存在著密不可分的關系.民機系統維修規(guī)劃的關鍵是制定最優(yōu)維修間隔,以減少非例行維修次數并提高飛機部件的可靠性[1].

針對維修間隔優(yōu)化的問題,Ahmadi等[2]對“非安全影響”和“安全影響”類別的隱藏故障,采用風險約束優(yōu)化的方法,得出單位飛行小時成本最小的維修間隔,但該方法未能考慮預防維修成本,影響了模型優(yōu)化結果的準確性.申桂香等[3]利用兩參數威布爾分布進行故障數據建模,確定出可用度最大情況下的預防維修間隔,忽略了經濟性因素對維修間隔優(yōu)化的影響,且使用兩參數威布爾擬合故障數據較三參數威布爾擬合精度不足.劉濤等[4]運用傳統的三參數威布爾極大似然估計法確定分布參數,該方法需要求解3個超越方程得到參數的估計值,由于三參數威布爾分布不滿足一般的正則條件,有時似然估計值不存在,因此,具有一定的局限性.賈寶惠等[5]運用經濟性分析的方法確定維修間隔時,雖然考慮了可靠壽命安全門檻值,但未建立可靠壽命區(qū)間約束下的維修費用率優(yōu)化模型,影響了維修間隔優(yōu)化的準確性.張鵬等[6]提出采用數值搜索方法求解飛機部件預防性維修模型,該方法較為繁瑣,且所得結果有一定的誤差.

針對上述方法存在的問題,本文提出運用改進的三參數威布爾極大似然估計法,對歷史故障數據進行可靠性分析,并建立了可靠壽命區(qū)間約束下的部件最優(yōu)定時維修費用率模型,針對復雜函數模型一般非線性規(guī)劃方法無法求解的情況,運用Matlab遺傳算法工具箱進行求解,快速準確地逼近最優(yōu)解,得到了部件最優(yōu)定時維修間隔期,為維修間隔的確定提供了可行的方法.

1 系統部件可靠性分析

1.1 三參數威布爾分布

若隨機變量T服從三參數威布爾分布,則其概率密度函數為[7]

(1)

累計失效概率函數為

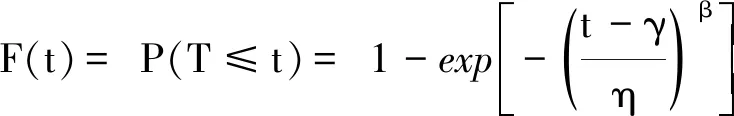
(2)

式中:β>0為形狀參數;η>0為尺度參數;γ≥0為位置參數.

可靠度函數為

(3)

可靠壽命為

(4)

1.2 三參數威布爾參數估計

三參數威布爾參數估計方法較多,常用的有線性回歸估計法、圖解法和極大似然估計法.綜合考慮,本文運用改進的極大似然法(Maximum Likelihood Estimation,MLE)進行模型參數估計的求解.

對于三參數威布爾分布,其對數極大似然函數為

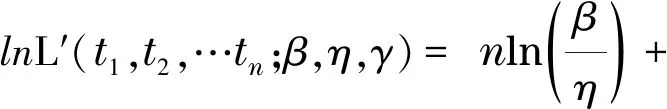
(5)

令

求解后得到lnL′的極值.

由于對數似然方程不能對位置參數γ進行求導,因此,先確定其估計值,然后用最大似然估計得出另外兩個參數.求解方程組為

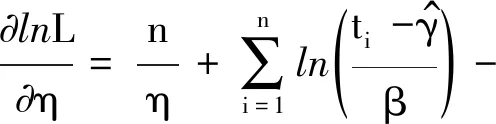
(6)

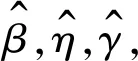
1.3 不同故障影響類型的可靠壽命推斷

在維修間隔的確定過程中,維修領導小組(Maintenance Steering Group-3,MSG-3)可以深入分析民機系統并選擇合適的可靠度.由波音787PPH提供的方法,得出不同故障影響類別下的可靠壽命方程[5].對失效函數符合三參數威布爾分布的部件,結合式(4)建立了適合不同故障影響類型的維修項目可靠壽命方程,即

(7)

式中:C=5為明顯安全性,C=8為隱蔽安全性,5,8類故障類別可靠度取0.9;C=6為明顯使用性,6類故障影響類別可靠度取0.8;C=7為明顯經濟性,C=9為隱藏非安全性,7,9類故障類別可靠度取0.7.

2 系統部件目標優(yōu)化

定時維修有兩種類型:定時拆修和定時報廢.其確定預防性維修間隔的方法相同,且僅適用于具有耗損期的產品[8].

民機系統部件通常進行預防維修,以減少意外停機損失,即獲得最佳的預防性維修間隔使維修活動的單位時間成本(Gost Per Unit Time,CPUT)最小[9].數學表達式為

(8)

式中:C(T)為單位時間成本(CPUT);EI平均周期長;EC為單個周期內的期望損失.

平均周期長為[9]

(9)

單個周期內的期望損失為

(10)

定時維修單位費用為

(11)

式中:Cf,CP分別為一次故障后維修和預防性維修的費用損失.

基于可靠壽命的維修費用優(yōu)化模型為

(12)

求解最優(yōu)維修間隔時,一般通過維修費用率函數C(T)對T求導,由于函數模型較為復雜,無法直接求C(T)對T的導數,因此,采用遺傳算法求解方程得到最優(yōu)維修間隔.

3 遺傳算法

遺傳算法最早由美國密西根大學Holland[10]教授于1975年提出,主要運用生物進化中的“適者生存”規(guī)律,即最適合自然環(huán)境的群體往往會產生更多的后代.對于復雜的目標函數優(yōu)化問題,遺傳算法可跳出局部最優(yōu),并找到全局最優(yōu)解[11].

遺傳算法運算步驟如圖1所示.

由圖1所示運算步驟,采用Matlab遺傳算法工具箱(Genetic Algorithm Toolbox),對維修費用率目標函數進行最優(yōu)化求解.

4 實例分析

4.1 故障數據采集

采集某航空公司2012年1月—2017年12月空客A320機隊空調系統的流量控制活門(Flow Control Valve,FCV)歷史故障數據(Time Since New,TSN),如表1所示.

圖1 遺傳算法流程圖Fig.1 Genetic algorithm flow chart

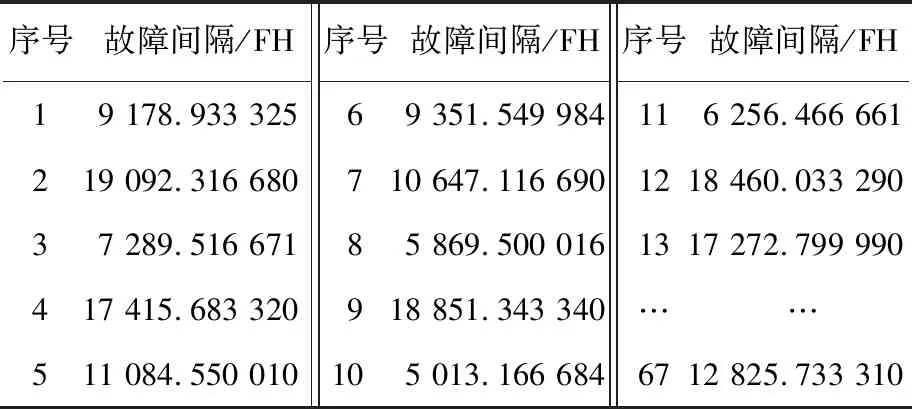
表1 空客A320 FCV故障數據Tab.1 Airbus A320 FCV fault data

注:FH為飛行小時(Flight Hours).

4.2 分布模型驗證與參數估計

利用Matlab軟件,對采集的故障數據進行三參數威布爾分布檢驗,得出如圖2所示概率圖.

圖2中各點近似一條直線,擬合效果較好,由此可判斷故障數據符合三參數威布爾分布.運用改進的極大似然估計方法,將故障壽命數據代入Matlab程序,求解模型參數估計值如表2所示.

圖2 FCV故障時間的概率圖Fig.2 FCV failure time probability graph

尺度參數η形狀參數β位置參數γ12 042.13.1421 823

由表2可知,1<β<4屬于耗損壽命型,可以通過優(yōu)化預防性維修間隔,提高部件的可靠性和使用壽命.

可靠度函數為

(13)

通過對FCV故障后果的分析,符合MSG-3中第6類故障影響類別,對于非安全類維修任務,考慮在合理的可靠度范圍內取最經濟的維護間隔,將其可靠度限制在[0.8,0.9]區(qū)間.由式(7)可得可靠壽命區(qū)間tR=(7 707,9 294).FCV的可靠度函數曲線,如圖3所示.

圖3 FCV可靠度函數曲線Fig.3 FCV reliability function curve

4.3 維修間隔優(yōu)化

已知平均預防性維修費用CP為4 500(元),平均故障后維修費用Cf為17 720(元).將維修項目壽命分布函數和各已知參數帶入式(12)中,以可靠壽命區(qū)間作為約束條件,將部件單位時間維修費用最低作為優(yōu)化目標,討論維修費用率在區(qū)間(7 707,9 294)上的最小值情況.費用率隨維修間隔的變化曲線,如圖4所示.

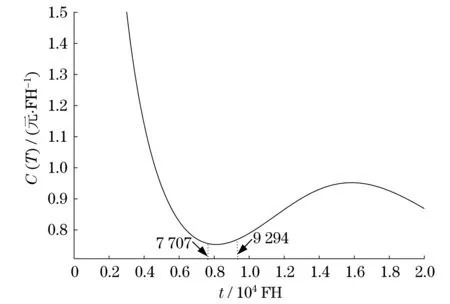
圖4 FCV費用率函數曲線Fig.4 FCV cost rate function curve

利用Matlab遺傳算法工具箱(GA Toolbox)求解維修費用率模型計算獲得,當t=8 111.3 FH時,存在最小成本率C(t)=0.753 2(元/FH).查閱FCV維修技術報告可知,該部件預防性維修任務間隔為8 000 FH,誤差比為1.39%,在合理的誤差范圍內,說明本方法可行.并且在保證可靠性的前提下,提高了維修任務的經濟性,節(jié)約了航空公司維修成本.

5 結論

(1) 對非安全類的維修任務,基于可靠性數據分析方法,結合MSG-3邏輯決斷法,推斷出可靠壽命區(qū)間.

(2) 建立了維修費用率優(yōu)化模型,通過三參數威布爾分布模型參數估計,得到故障壽命數據的可靠度函數和累積分布函數,代入維修費用率優(yōu)化模型,在滿足可靠壽命區(qū)間范圍內,使用遺傳算法獲得最小維修費用率對應的維修間隔,使制定的維修間隔在保證部件可靠性的同時減少維修成本.為民航維修規(guī)劃時,制定合理的維修計劃提供了理論依據.