Almost Sure Convergence of Weighted Sums for Extended Negatively Dependent Random Variables Under Sub-Linear Expectations
WANG Wenjuan(王文娟),WU Qunying(吳群英)
(College of Science,Guilin University of Technology,Guilin 541006,China)
Abstract: In this thesis,we discuss almost sure convergence of weighted sums for END random variables with the condition of CV(|X|p)<∞,even (|X|p)≤CV(|X|p),0
Key words: Weighted sum;Sub-linear expectation;Almost sure convergence;END random variables
1.Introduction
As is well known that limit theorems exert a enormous function on probability limit theory and mathematical statistics.It becomes a vital theoretical tool to study the phenomenon of randomness or uncertainty.In fact,probability measures and linear additivity themselves do not account for many of the uncertainties in statistics,measures of risk,mathematical economics and super-hedging in finance.[4,6?7,8?11]In order to solve this problem,PENG[10?12]established a new system of nonlinear expectations theory from a completely new perspective.This theory does not start from the classical probability space but directly define the independence of random variables from the non-linear expectation space,and proves the theoretical basis of nonlinear expectation with PDE.
The sub-linear expectation created a lot of fascinating properties which are different from those of the linear expectations.So the limit theorems of the sub-linear expectations have been received a lot of attention and research recently.A great deal of useful results have been established by many researchers.For instance,PENG[10?11]established the basic properties,denoted the relevant definition of notation and distribution and a new central limit theorem in the nonlinear expectation space.CHEN[3]studied three variety of strong laws of larger numbers under the feasible condition of(|X|1+α)<∞for independent identically distributed random variables.ZHANG[17?19]found the the laws of the iterated logarithm for negatively dependent random variables in a successive non-linear expectation.He also established Kolmogorov’s exponential inequalities and the rosenthals inequalities which are the powerful tools for future research in the sub-linear expectation.
Almost sure convergence is one of the most important issues in limit theorems.In sublinear expectations,due to the uncertainty of expectation and capacity,the strong convergence is essentially different from the ordinary probability space.The study of strong convergence for sub-linear expectations is much more complex and difficult.As a result of the extensive utility of weighted sums in financial statistics,many scholars put emphasis on its properties.Numerous studies on almost sure convergence of weighted sums can be found in probability space.For example,CHOI and SUNG[1]gained the diverse conditions on{ani}and{Xn}under which ∑n i=1aniXiconverges to zero almost surely.CHEN and GAN[2]established the strong laws of large numbers,laws of the single logarithm and Chover’s laws of the iterated logarithm (LIL) for weighted sums of i.i.d.random variables under appropriate conditions concerning both the distribution and the weights.TEICHER[14]researched a Marchinkiewicz-Zygmund type strong law for the special caseXU and YU[15]obtained the law of the single logarithm for NA random variables with the condition ofWU[16]acquired a strong limit theorem for weighted sums of ND random variables.The prime motivation of the article is to gain the almost sure convergence for weighted sums of END random variables with the condition ofCV(|X|p)<∞,even(|X|p)≤CV(|X|p),0
2.Preliminaries
The study of this article utilizes the symbols and framework which are established by PENG[10?12].He established the definitions of sub-linear expectation (?E),subadditivity of capacities V,Choquet integrals/expectations (CV,Cv) and some of the properties,and so on.As a result,we can omit these various definitions and relevant properties.
Under the sub-linear expectation space,CHEN[3]and ZHANG[17?18]researched such a kind of convergence,but they don’t have a specific summary.So,we summarize the definition of almost surely as follows.
Definition 2.1A sequence of random variables{Xn;n ≥1}is named to converge toXalmost surelyV(a.s.V),denoted byXn →Xa.s.Vasn →∞,ifV(XnX)=0.
Vcan be substituted for V andvseverally.Byv(A)≤V(A) andv(A)+V(Ac) = 1 for anyA ∈F,it is obvious thatXn →Xa.s.V impliesXn →Xa.s.v,butXn →Xa.s.vdoes not implyXn →Xa.s.V.Further

and
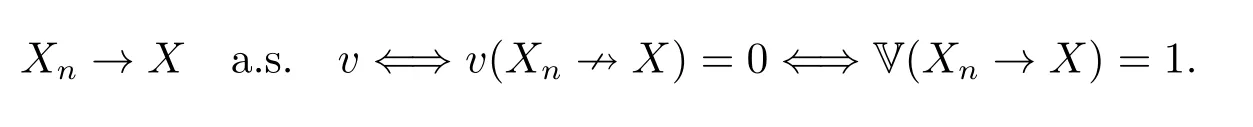
Remark 2.1In probability space,it’s commonly known thatXn →Xa.s.??P(Xn →X)=1??P(XnX)=0 fromP(A)+P(Ac)=1.However,in the sub-linear expectation space,the formula V(A) + V(Ac) = 1 is no longer valid,which implies V(Xn →X) =1V(XnX) = 0.In fact,we have V(XnX) = 0 =?V(Xn →X) = 1,but V(Xn →X) = 1V(XnX) = 0.Therefore,we can’t defineXn →Xa.s.V with V(Xn →X)=1.
Definition 2.2[13]A couple of (V,v) of capacities under the sub-linear space (?,H,?E)is indicated by
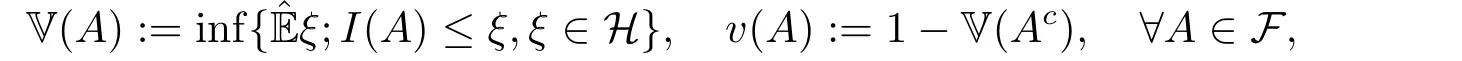
whereAcis the supplement series ofA.By definitions of V andv,it is distinct that V is sub-additive,and
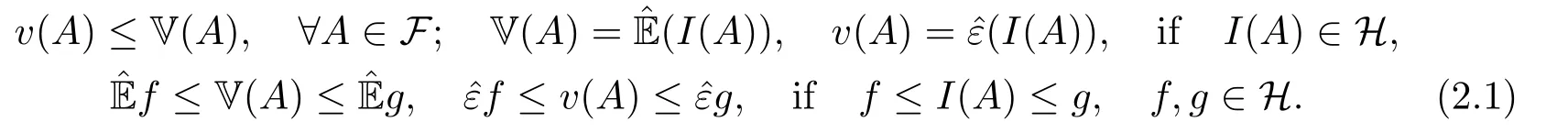
Definition 2.3[13](Identical distribution)Assume that X1and X2are twon?dimensional random vectors established separately in sub-linear expectation spacesand(?2,H2,).They are named identically distributed,denoted by
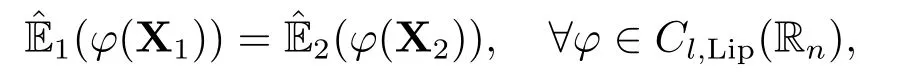
whenever the sub-expectations are limited.A sequence{Xn;n ≥1}of random variables is referred to as identically distributed,for eachi ≥1 if
Definition 2.4[17](Extended negative dependence) A sequence of random variables{Xn;n ≥1}is called upper (resp.lower) extended negatively dependent if there is some leading constantK ≥1 such that
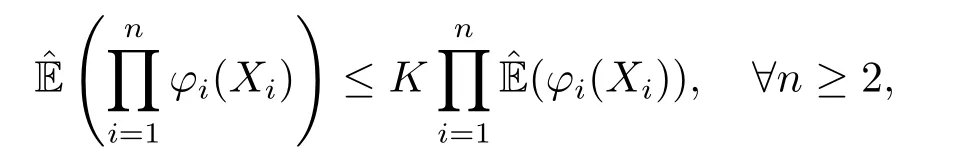
whenever the sub-expectations are finite and the non-negative functionsφi(x)∈Cl,Lip(Rn),i=1,2,...,are all non-decreasing (resp.all non-increasing).They are named extended negatively dependent if they are both upper extended negatively dependent and lower extended negatively dependent.
We can easily see that,if{Xn;n ≥1}is a sequence of independent random variables andf1(x),f2(x),...∈Cl,Lip(Rn),then{fn(Xn);n ≥1}is also a sequence of independent random variables with K = 1;if{Xn;n ≥1}is a sequence of upper (resp.lower) extended negatively dependent random variables andf1(x),f2(x),...∈Cl,Lip(Rn) are all non-decreasing (resp.all non-increasing) functions,then{fk(Xk);k ≥1}is also a sequence of upper (resp.lower)extended negatively dependent random variables.
By the definition,it is visible that,if Y is independent to X,then Y is extended negatively dependent to X.Example 1.6 in [18] indicates that the reverse is not true.
Example 2.1[18]Assume thatPis a family of probability measures defined on (?,F).For any random variableξ,we indicate the upper expectation by(ξ)=supQ∈PEQ(ξ).Then(·) is a sub-linear expectation.Moreover,if X and Y are independent under eachQ ∈P,then Y is extended negatively dependent to X under.In reality,
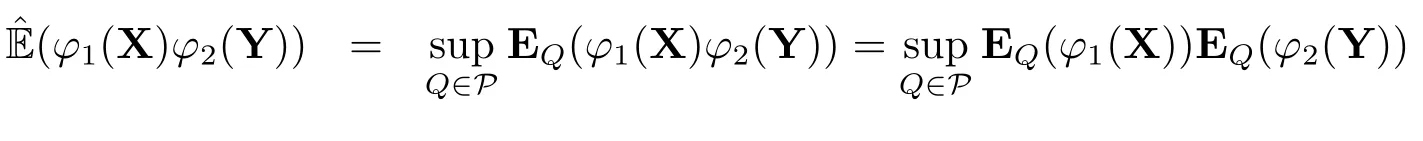
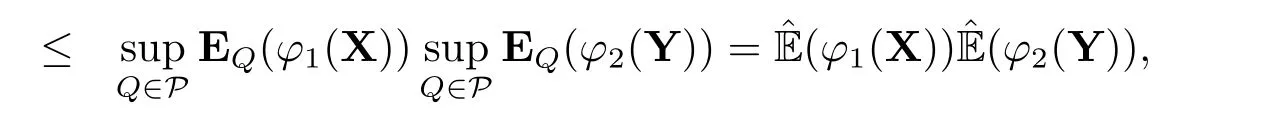
whenever the sub-expectations are finite andφ1(X)≥0,φ2(Y)≥0.
However,Y may be not independent to X.
3.Results and Discussions
In this section,we discuss our primary result and some useful lemmas.Next,we have a convention,let{Xn;n ≥1}be a sequence of random variables inandThe symbolcis on behalf of a generic positive constant that may be different in various place.Letan ?bnmean that there exists a constantc>0 such thatan ≤cbnfor adequately largen,andI(·) denotes an indicator function.logxis a mark of ln(max(x,e)),where ln is the natural logarithm.
For the proof of our theorem,we declare the following two lemmas.
Lemma 3.1( Borel-Cantelli’s Lemma,Lemma 3.9 in [18]){An;n ≥1}is a sequence of events inF.Suppose thatVis a countably sub-additive capacity.thenV(An;i.o.)=0,where
Lemma 3.2( Theorem 3.1 in [17]){Xn;n ≥1}is a sequence of upper extended negatively dependent random variables inand there exists a constantK >0.Then for allx,y >0,
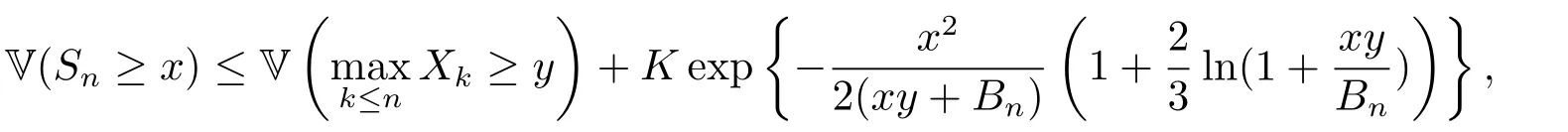
where
The following theorem is the result of the main discussion in this article.
Theorem 3.1Suppose that 0
0 satisfying

Ifp ≥1 further assume that

Let{ank;1≤k ≤n,n ≥1}be an array of real positive numbers such that
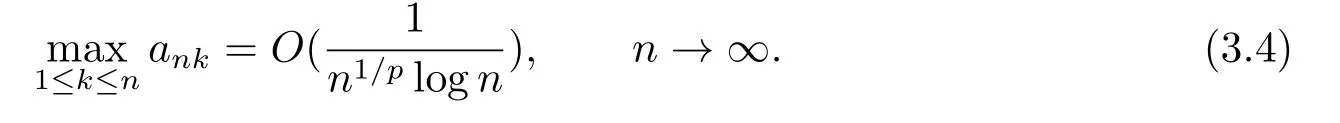
Then
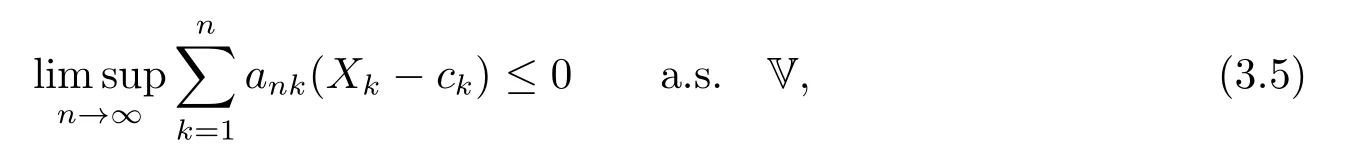
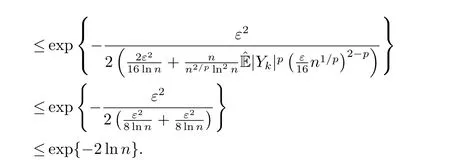
whereck=0 if 0 Further,if{Xn;n ≥1}is lower extended negatively dependent,then In particular,if{Xn;n ≥1}is extended negatively dependent andXk=Xkfor 1≤p ≤2,then Remark 3.1Theorem 3.1 generalizes SILVA’s result from probability space to sublinear expectation space,which improves SILVA’s conclusion to some extent.Secondly,in sub-linear expectations,ZHANG[17]studied partial sums,and we study the weighted sums in Theorem 3.1.Becauseank= 1 is a condition that does not satisfy the condition(3.4)of Theorem 3.1,the above theorem is different from the strong number theorem studied by ZHANG. Remark 3.2According to Definition 2.4,in the sub-linear expectation,the END sequence is a very broad dependent sequence.IfK=1,then the END sequence is a extended independent sequence.IfK=1,n=2,then the END sequence is an ND sequence.Therefore,in the sub-linear expectation,Theorem 3.1 is still valid for extended independent sequences and ND sequences. Proof of Theorem 3.1Without loss of generality,forp ≥1,we can suppose thatXk= 0.Obviously,CV(|X|p)<∞is equivalent toCV(|X|p/cp)<∞for anyc >0.We have Note that Therefore,(3.2) is equivalent to for anyc>0, Note that Hence,by (4.1),it indicates that For upper extended negatively dependent random variables{Xn;n ≥1},in order to ensure that the truncated random variables are also upper extended negatively dependent,we need that truncated functions belong toCl,Lipand are non-decreasing.Letfc(x)=?cI(xc),for any 1≤k ≤n,n ≥1, and Then{Yk;1≤k ≤n,n ≥1}is also a sequence of upper extended negatively dependent random variables byfc(x)∈Cl,Lipandfc(x) being non-decreasing. Note that Thus,to prove (3.5),it suffices to verify that It should be pointed out that (3.1) does not imply V(h(Xn)∈A)≤V(h(X1)∈A).Therefore,in the calculation of V(f(Xn)∈A),we need to convert V toby (2.1).On the other hand,in the probability space,there is an equality: EI(|X|≤a)=P(X ≤a),however,in the sub-linear expectation space,is defined through continuous functions inCl,Lipand the indicator functionI(|X| ≤a) is not continuous.Therefore,the expression(|X| ≤a)does not exist.This needs to modify the indicator function by functions inCl,Lip.To this end,we define the functiong(x)∈Cl,Lipas follows. For 0<μ<1,letg(x)∈Cl,Lip(R) such that 0≤g(x)≤1 for allx,g(x)=1 if|x|≤μ,andg(x)=0 if|x|>1.Then Thus,V(Zk≠0,i.o.) = 0 follows from the Borel-Cantelli’s lemma (Lemma 3.1) and V being countably sub-additive.It follows that from (3.4) Now,we prove that|I3| →0,asn →∞.For anyr >0,by thecrinequality and (4.4),we have Thus, holds from (3.1) and (4.4). Case 1 0 By (4.1) and V(|X|>μn1/p)↓,so we get It follows that Next,we estimateI31.Letgj(x)∈Cl,Lip(R),j ≥1 such that 0≤gj(x)≤1 for allx, Then For everyn,there exists a constantksuch that 2k?1≤n<2k,thus,by (4.8),g(x)↓,we get By (4.2),it follows that Combining (4.7) with (4.9),we get Case 2p ≥1. Once again,using (3.2)-(3.4),we have By (4.10) and (4.11),we get Finally,we estimateI2.Becauseis a sequence of upper extended negatively dependent random variables withand satisfies the conditions of Lemma 3.2.By the condition (3.4),ank →0,without loss of generality,we can suppose thatank ≤1,and letthenfor sequenceBy Lemma 3.2,we obtain for every?>0, So, According to the Borel-Cantelli’s lemma and arbitrariness ofε,we haveYk)>?;i.o.)=0,that is to say, Together with (4.3),(4.5),(4.12) and (4.13),we can get (3.5). If{Xn;n ≥1}is lower extended negatively dependent,then{?Xn;n ≥1}is upper extended negatively dependent and{?Xn;n ≥1}satisfies the condition of Theorem 3.1.Letting{?Xn;n ≥1}instead of{Xn;n ≥1}in (3.5),we have namely, and we can get (3.6).Therefore,the proof of Theorem 3.1 is completed. We have obtained the almost sure convergence of weighted sums under sub-linear expectations.We point out that the key tools to the proofs of the main results of SILVA[5]are not suitable for our theorem.We propose the new method to prove our result.Moreover,the theorem of our paper not only extends the corresponding results of SILVA[5]under sub-linear expectation space,but also is proved with the conditions ofCV(|X|p)<∞andfurther(|X|p)≤CV(|X|p)<∞,0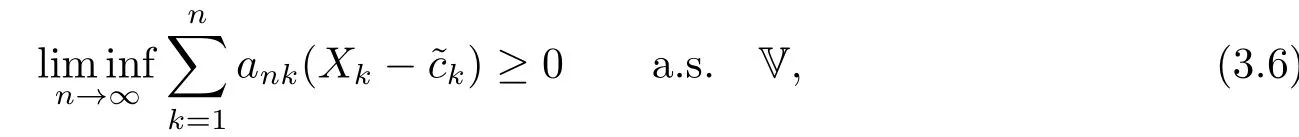

4.Proof

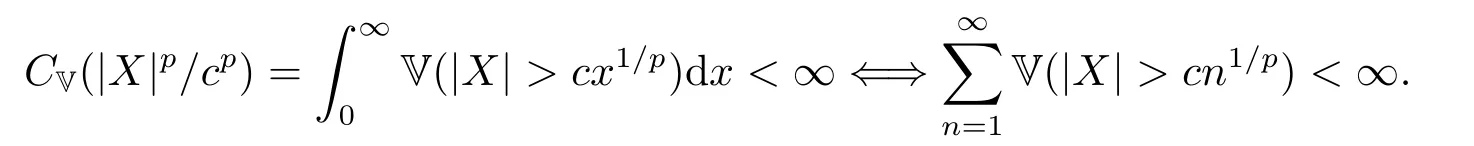

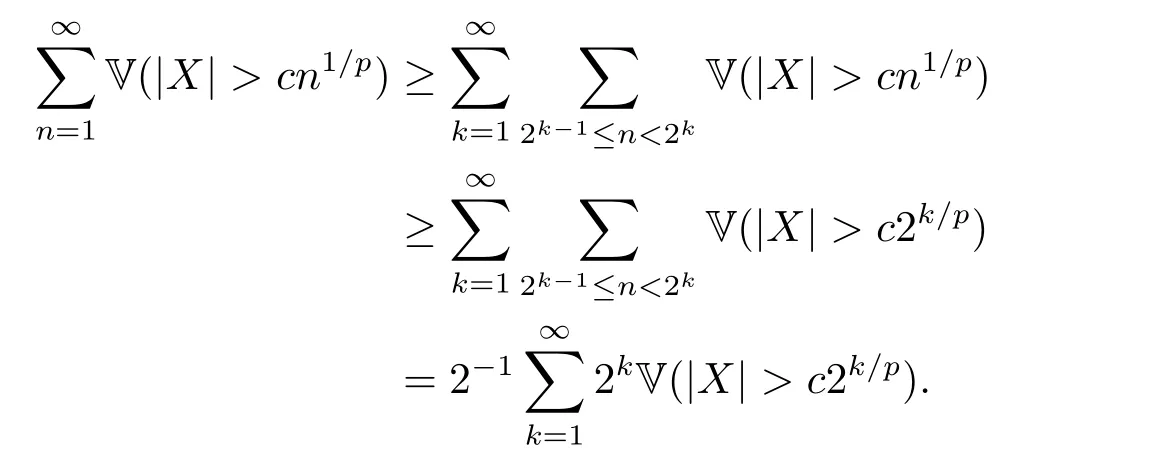
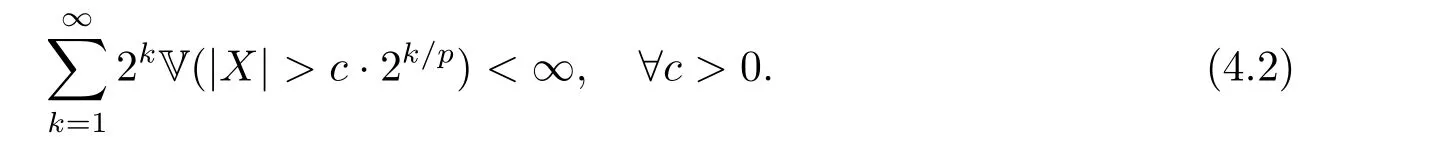
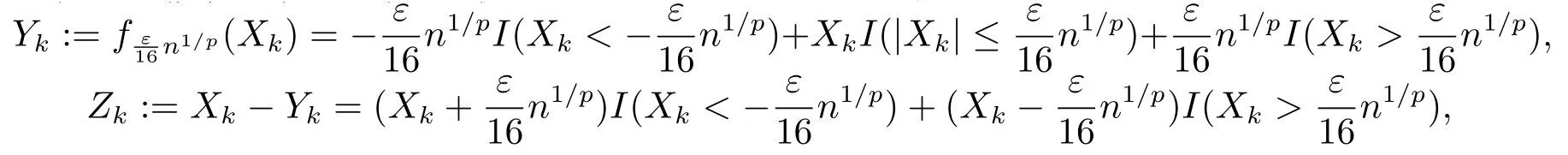
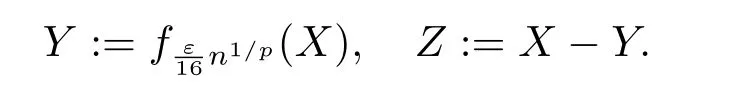
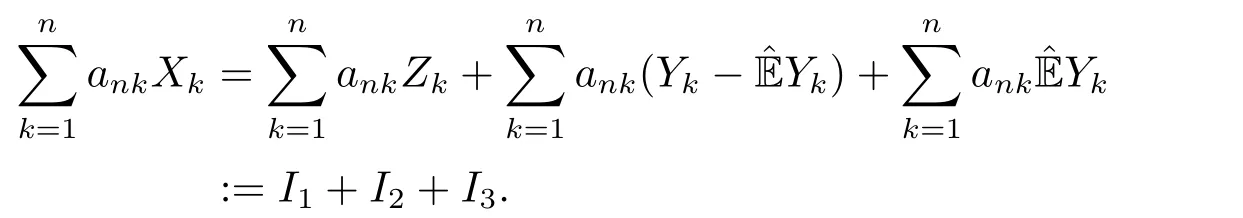
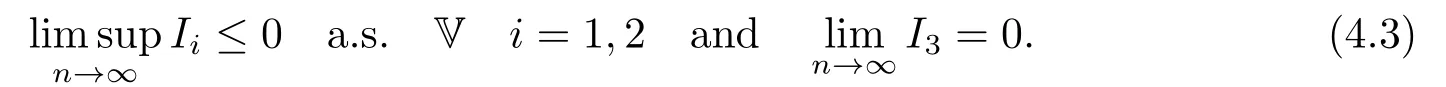
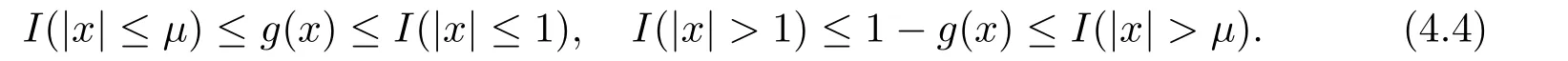
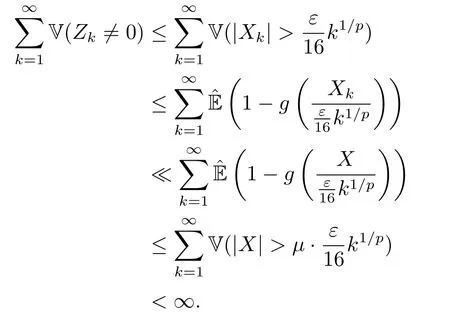
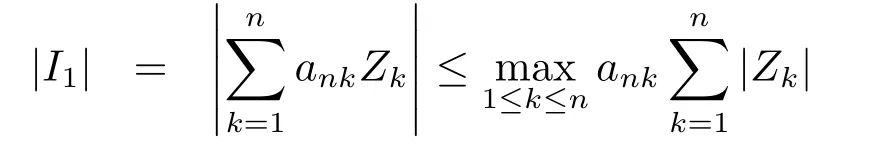
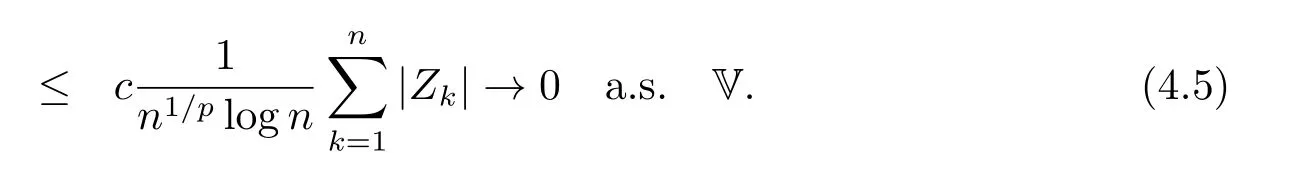
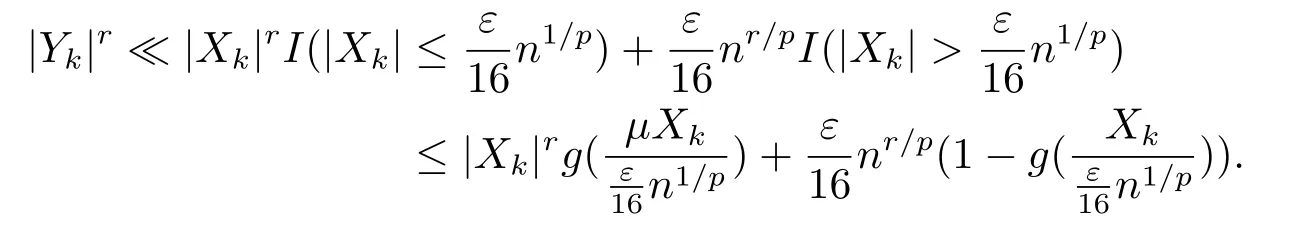
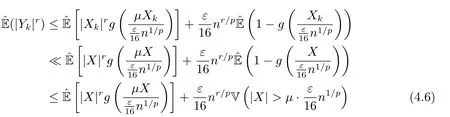
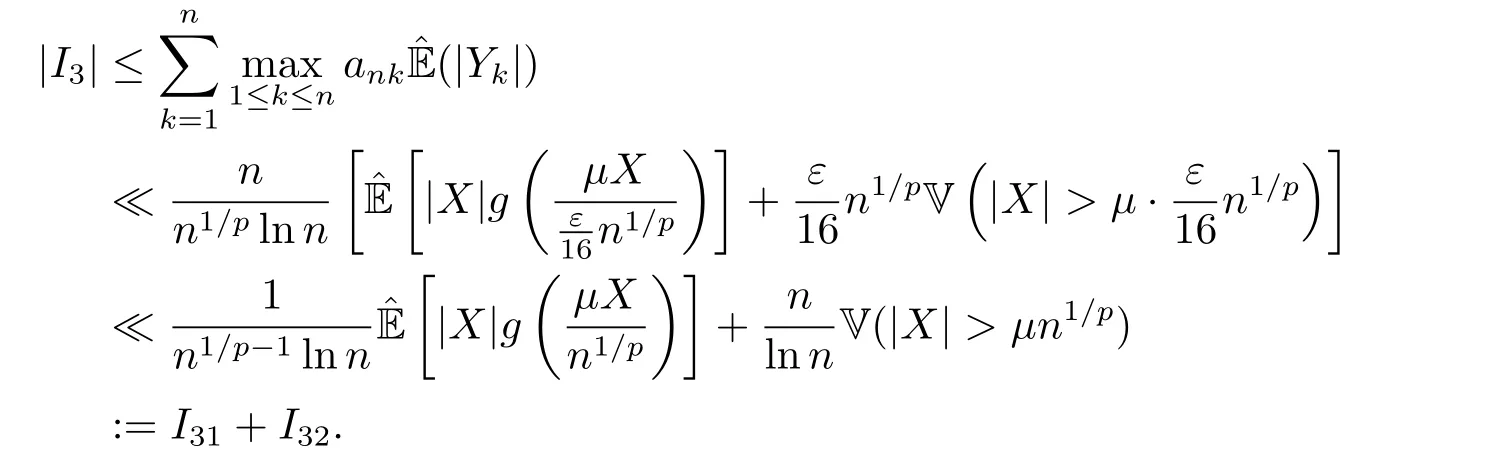

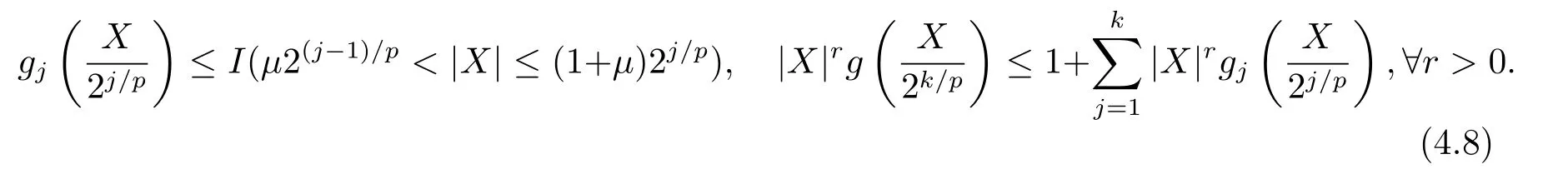
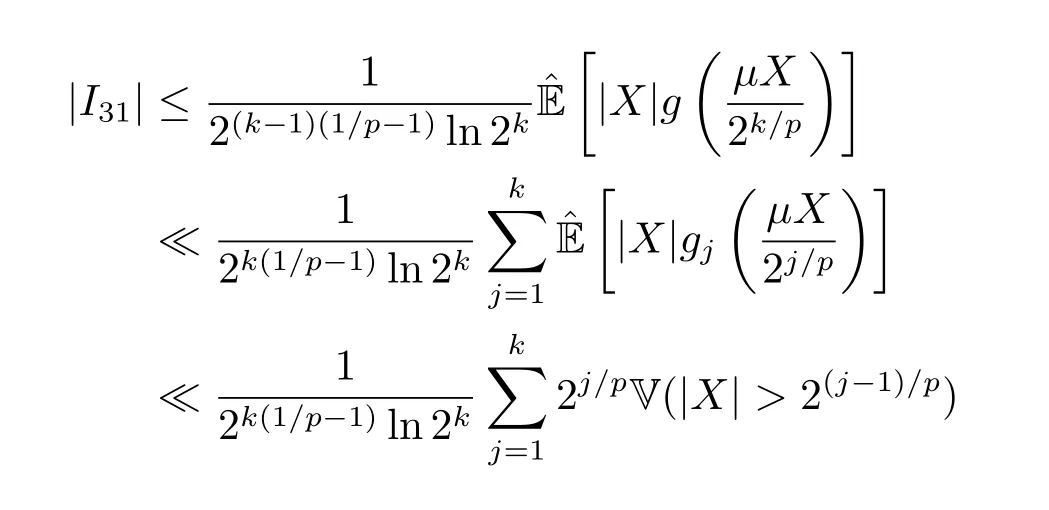
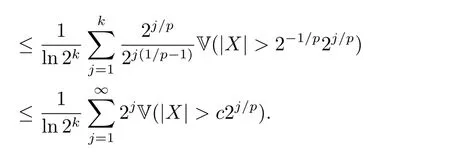


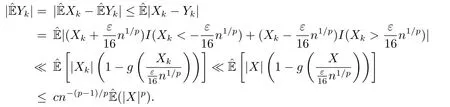
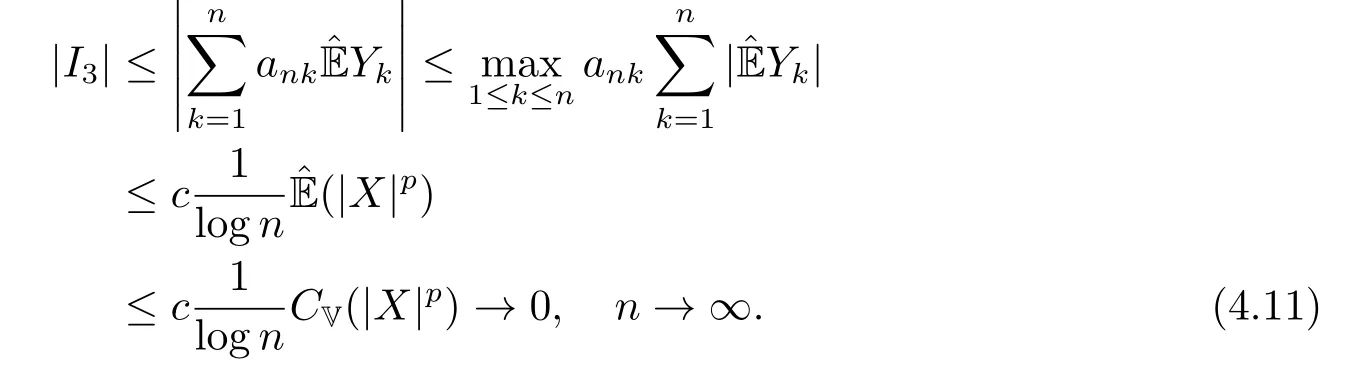

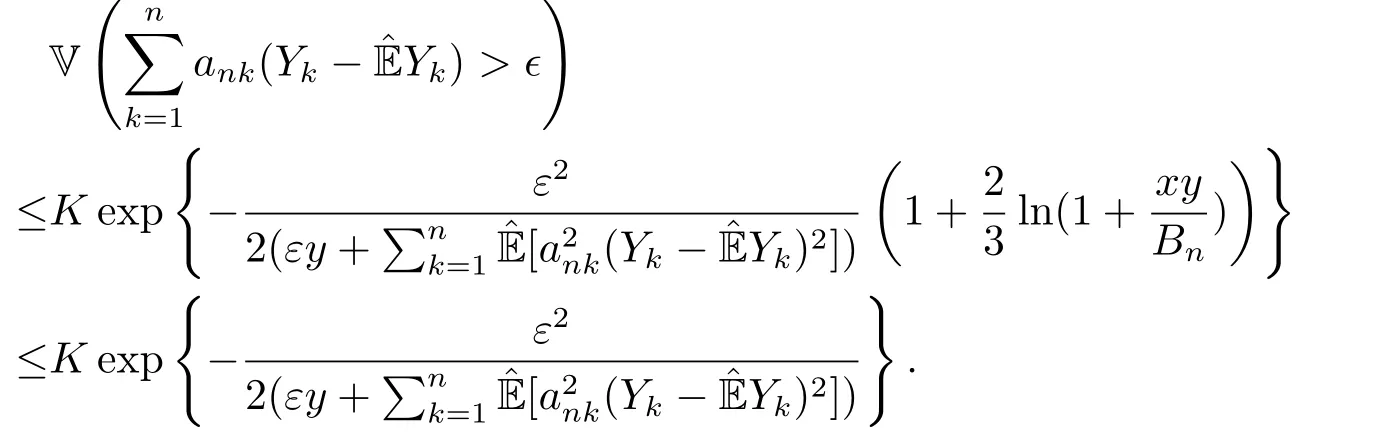
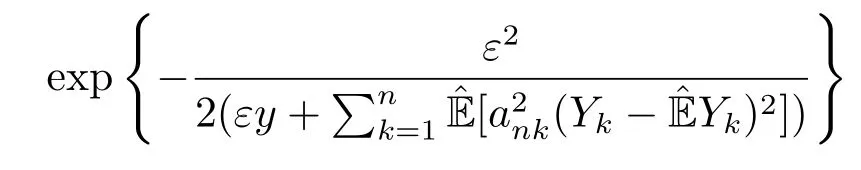



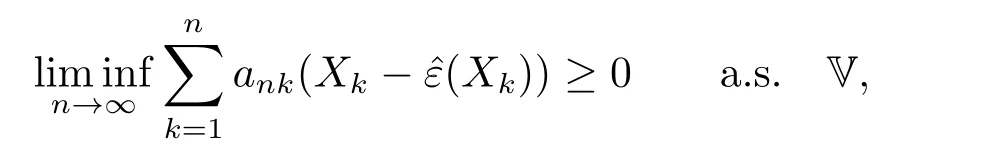
5.Conclusions

