SYMMETRY OF SOLUTIONS OF MONGE-AMPèRE EQUATIONS IN THE DOMAIN OUTSIDE A BALL
ZHANG Yun-xia,JIAN Huai-yu
(1.Public Class Teaching Department,Shanxi Financial and Taxation College,Taiyuan 030024,China)
(2.Department of Mathematical Sciences,Tsinghua University,Beijing 100084,China)
Abstract:We study the symmetry of solutions to a class of Monge-Ampère type equations in the domain outside a ball.By using a moving plane method and the transform introduced by Jian and Wang,we prove the radially symmetry of the solutions.
Keywords:symmetry solution;Monge-Ampère equation;moving plane;extreme principle
1 Introduction
In this paper,we study the radially symmetry of solutions to the equation in the form of
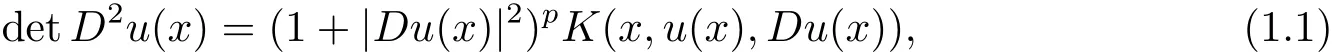
When K(x,u(x),Du(x))=[(xDu(x)?u(x)]n+2and p=0,(1.1)is the equation of the well-known affine hyperbolic sphere,and its Bernstein property,which may implies the symmetry under the normal condition(1.2),was studied in[6].Basing a transform introduced by Jian and Wang in[6],the authors in[7]studied the symmetry of solutions of(1.1)with K(x,Du(x),u(x))=[(xDu(x)? u(x)]βF(u(x))in the entire space Rn.They proved that a C4-strictly convex solution to(1.1)in Rnis the radially symmetric about the lowest point,say for example the origin,provided that
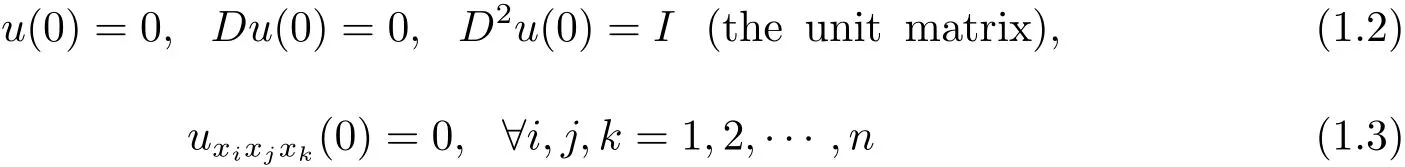
and

Obviously,the strict convexity,(1.2)and(1.4)are natural assumptions,which implies that for any small r>0,
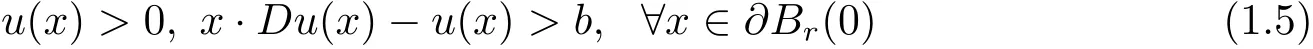
for some b>0.But assumptions(1.3)and the C4-smoothness for the solutions is too restrictive.
Recall that a C2-function h(x)is called strictly convex in ? if its Hessian matrix[D2h(x)]is positive definite in ?.
In this paper,we study the symmetry of solutions of(1.1)in the domain outside a ball.Interestingly,in this case we can remove assumption(1.3)and the smoothness of the solutions needs only C2.Our main result is the following theorem.
Theorem 1.1 Suppose that p,β ∈ R and
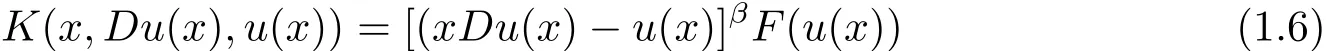
with F satisfies
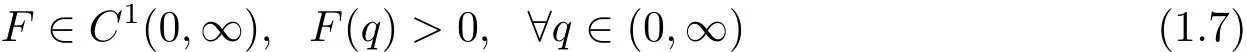
and

If there exist positive constants c,r,b such that u∈C2(RnBr(0))satisfies(1.1)in(1.4)and
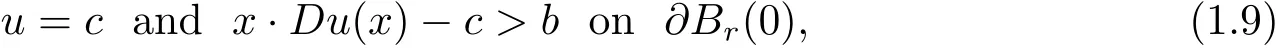
and if u is strictly convex,then u is radially symmetric in RnBr(0)about the origin.
By Theorem 1.1 and(1.5),it is easy to see that the main result in[7]still holds true if assumption(1.3)is replaced by the assumption that u is radially symmetric about the origin in Br(0)for some small r>0.
The radial symmetry for the positive solutions of the equations Δu+f(u)=0 for x ∈ Rnwas studied in[8]under the ground state conditions:u(x)→ 0 as|x|→ ∞.Afterwards,a lot of works were published along this direction,dealing with various symmetry problems for nonlinear elliptic equations.See,for example,[9–13]and the references in[7].However,all those symmetric results,up to authors’knowledge,need the a priori ground state condition,which can not be satisfied for solutions to Monge-Ampère equations.
The proof of Theorem 1.1 is done in Section 3;in Section 2,some lemmas necessary for the proof are given.
2 Some Lemmas
In[6],Jian and Wang introduced a transform which reduces the behavior of u near∞to that of the new function near the origin and preserves the form of equation(1.1).This transform is

where we assume u∈C2and u>0.Then

By calculations,we have
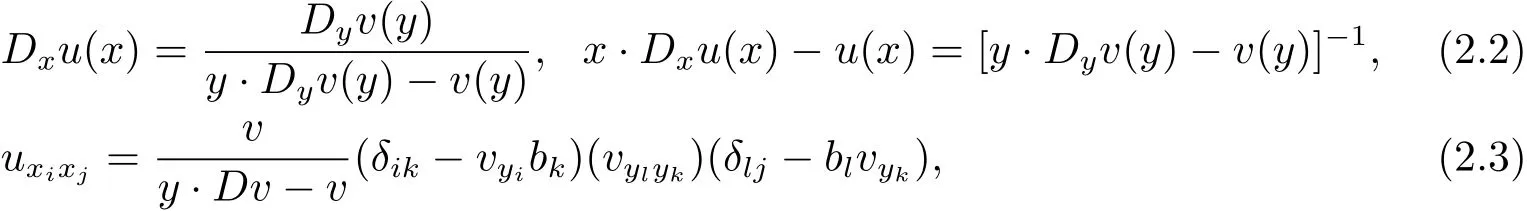
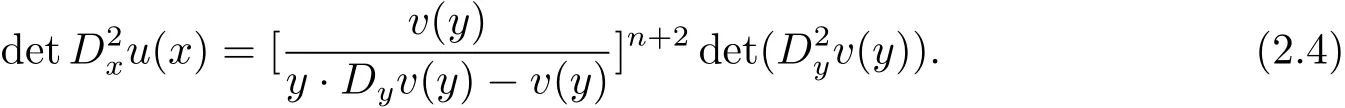
See(2.6)–(2.8)in[6]or(2.3)–(2.5)in[7].
Lemma 2.1 Suppose that a strictly convex function u∈C2(RnBr(0))satisfies(1.1)in(1.4),(1.6)and(1.9).Let y and v be given by(2.1).Then
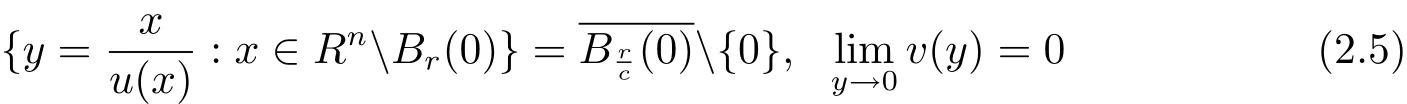
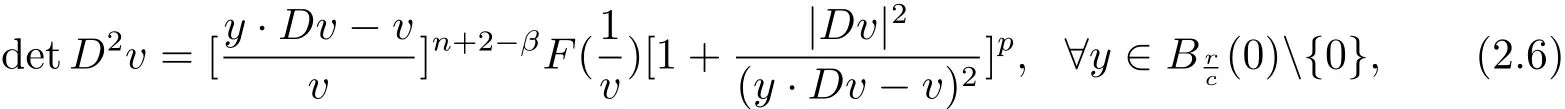
and
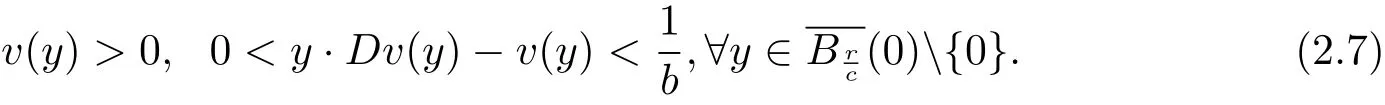
Proof Obviously,the convexity implies that u(x)≥c>0 for all x∈RnBr(0).To prove(2.7),we have,by(1.9)and the continuity,that u(x)?x·Du(x)< ?b for x near?Br(0).This means the intersecting point,(0,u(x)? x·Du(x)),between the supporting plane of the graph of u at(x,u(x))with the xn+1-axis is below the point(0,?b).Since the convexity preserves this property as x is away from?Br(0),we obtain
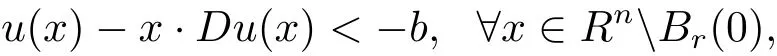
which,together with(2.2),implies(2.7).
Since?b< 0,the position of the supporting plane of the graph of u shows the graph{(x,u(x)):x near?Br(0)}is above the cone:x near?Br(0)},so the whole graph{(x,u(x)):is above the whole cone,i.e.,
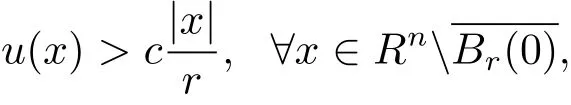
which implies
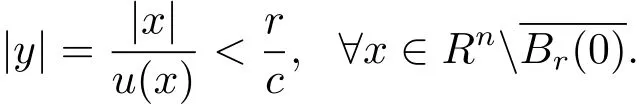
Obviously,
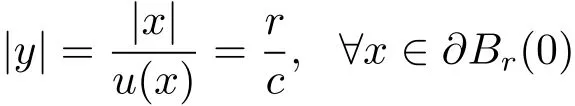
and
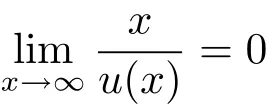
by(1.4)and(1.9).Hence,we obtain(2.5).
Now,by(1.1),(1.6),(2.2)and(2.3),we see thatis a strictly convex and positive function,satisfying(2.6).
Lemma 2.2 Let w ∈ C2(?)be a nonnegative solution to

where ? is an open set in Rn,aij,bi,C(x) ∈ L∞(?′)and the matrix[aij(x)]is positivedefinite in ?′for any compact set ?′?.Then either w≡0 in ? or w(x)>0 for all x∈ ?.Moreover,if w∈C2(?)TC1()and w(x0)>0 for some x0∈? and w()=0 for some∈?? which is smooth near,thenwhere ν is the unit outer normal of??.
The proof of Lemma 2.2 can be found in[14].
Lemma 2.3 Suppose that diam(?)≤ d,aij,bi,C(x)∈ L∞(?)and the matrix[aij(x)]is positive in.Let w∈C2(?)satisfies(2.8)andThere exists a δ> 0 depending only on n,d and the bound of the coefficients such that w(x) ≥ 0 in ? provided that the measure|?|< δ.
This lemma is exactly Proposition 1.1 in[9].
3 Proof of Theorem 1.1
Assume u∈C2(Rn)Br(0)is strictly convex,satisfies(1.1)in(1.4)and(1.9)with K satisfying(1.6)–(1.8).Replacing u by,we may assume c=1 in Theorem 1.1.Let y and v(y)be given by(2.1).It is enough to prove that v is radially symmetric about the origin in Br(0){0}.
It follows Lemma 2.1 that Thenis a strictly convex function,satisfying
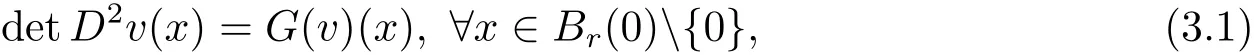
where
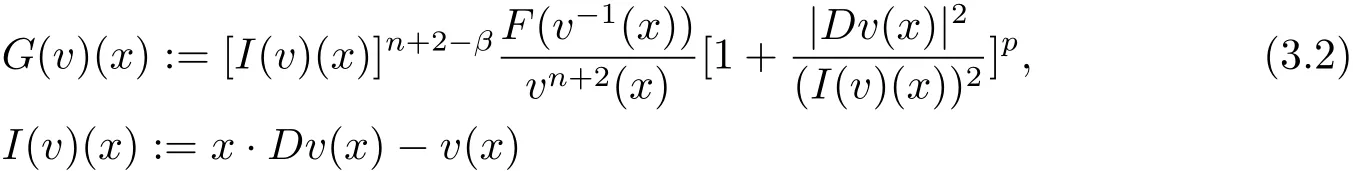
and
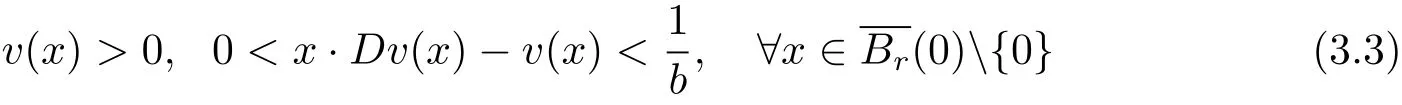
and
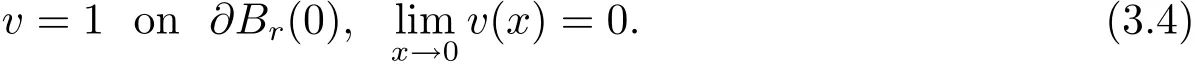
We will use the moving planes method to prove that v is radially symmetric with respect to the origin.This needs to show that v is symmetric in any direction with respect to the origin.Since equation(3.1)is invariant under orthonogal transforms,it is sufficient to do this in one direction.Without loss of generality,we will do it in e1-direction.In a word,to show Theorem 1.1,it is enough to prove that
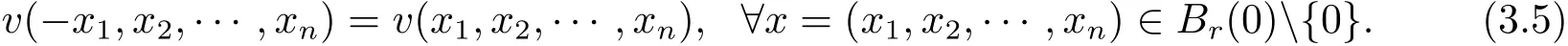
Use(x1,x′):=(x1,x2,···,xn)to denote a point x in Rn.For any λ ∈ R,denote
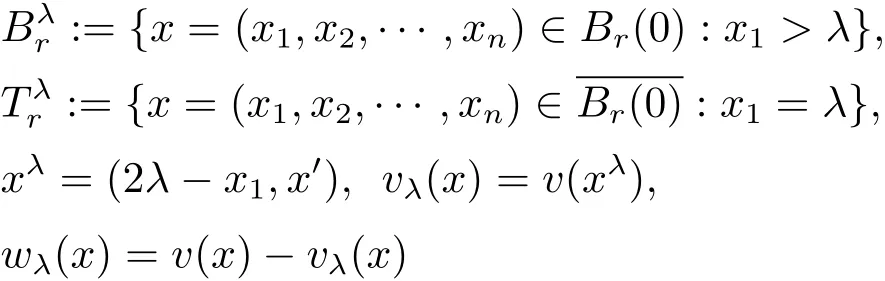
and
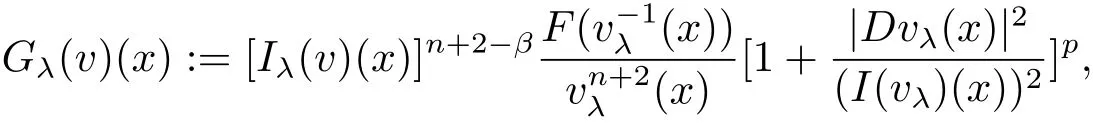
where

As in[7],we introduce the following differential operator
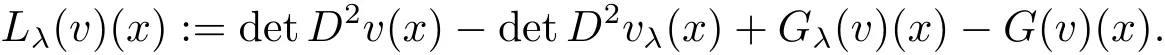
By assumption(1.7)and a mean value theorem,we have the following obvious result.
Lemma 3.1 Let r be any positive constant.Ifis bounded,positive and strictly convex,then for any compact ? inthere exist a constant C1> 0 independent of λ ∈ (0,∞)(but depending on ?)and piecewise continuous functions{(x)},{(x)},Cλ(x)(all depending on the v and its derivatives up to second order in ?),such that
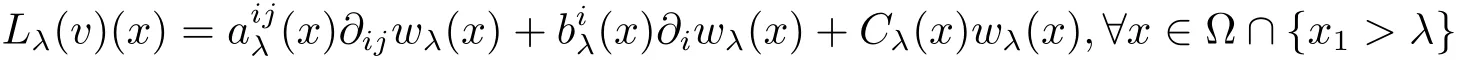
and
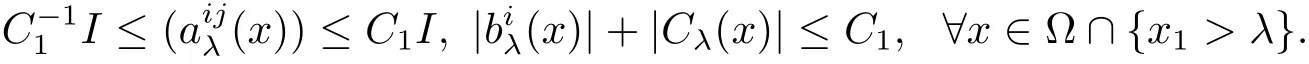
We will complete the proof of Theorem 1.1 after proving the following three claims.
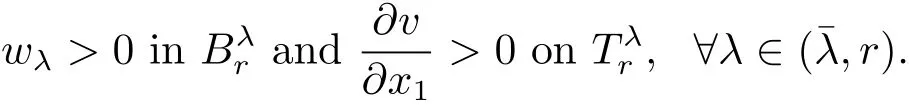
To show it,we see,by(3.1),(1.7)and(3.3),that

So,the usual strong maximum principle and Hopf’s boundary point lemma in[4]implies

and
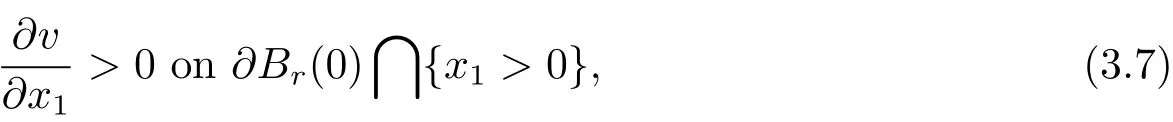
where we have used the fact that the angel between the vector(x1,x′)∈ ?Br(0)and the out normal of?Br(0)at the point x=(x1,x′)is less thanfor x1>0.
By continuity and(3.7),we see that that there is a λ1∈ (,r)such that
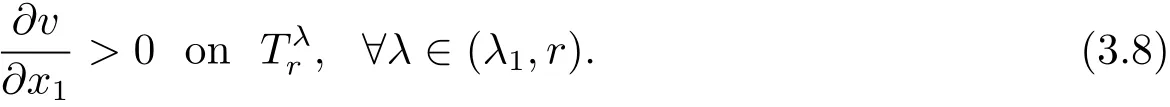
By(3.4)and(3.6),we see that
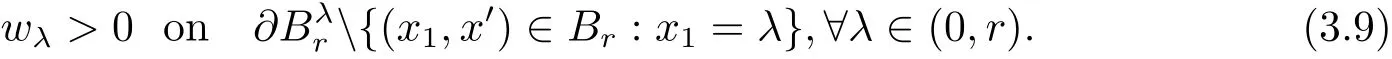
To complete the proof,we notice,for λ > 0 and λ < x1< 2λ,that
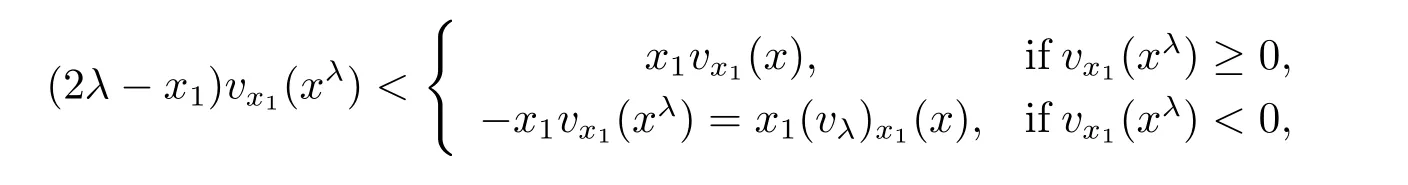
where we have used the fact vx1(xλ)< vx1(x)by the convexity.It follows that
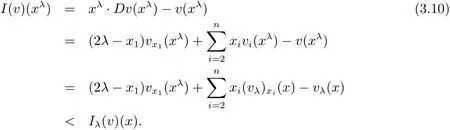
This,together with assumptions(1.8),implies
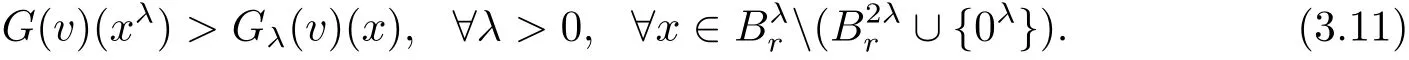
Noting detD2v(xλ)=detD2vλ(x)and using(3.11),we have,by equation(3.1),that
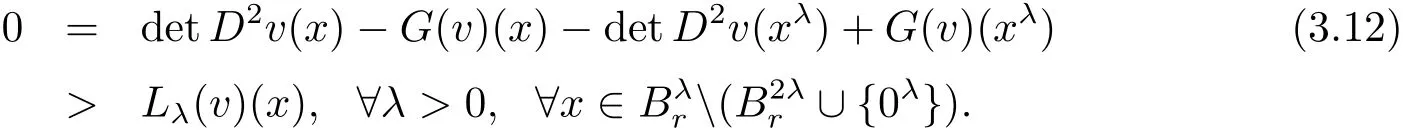
Observing that the measure ofcan be smaller than any positive constant if r?λ1>0 is small.Applying Lemmas 3.1 and 2.3 to(3.12),we obtain a constant∈(λ1,r)such that wλ≥0 infor all λ ∈[,r).Since λ is arbitrary in[,r),we have wλ≥0 in.Furthermore,Lemma 2.2 implies
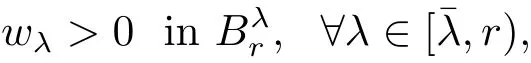
which,together with(3.7)and continuity,complete the proof of Claim 1.
Let
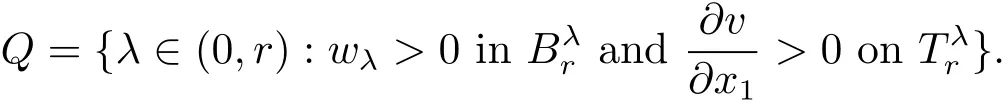
Claim 2 The set Q is open in(0,r).Suppose this Claim is false,i.e.,there exist a λ′∈Q and a number sequence λkand a sequence of points{xk}?such that
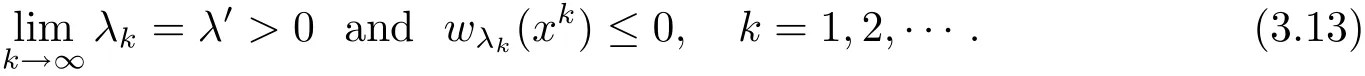
Otherwise,we have a sequence yk∈such that≤ 0,which implies immediately that(y)≤ 0 for some y∈,contradicting with λ′∈ Q.
Next,we want to get a contradiction by(3.13).First,by the boundedness of{xk},we can choose a subsequence such that

Then
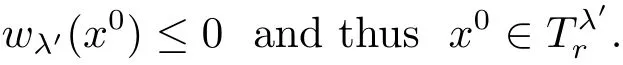
Because λ′∈ Q,we have

Sine(3.13)means that v(xk)≤ v((xk)λk),and

we see that
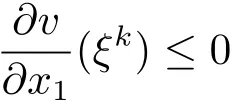
for some ξkin the segment connecting xkand(xk)λkfor k=1,2,···.Moreover,ξk→ x0by(3.14)and the factThen,,contradicting(3.15).This proves Claim 2.
Claim 3Let(λ0,r)be the connected component of Q in(0,r)containing[,r).Then λ0=0.
By the definition of λ0,we have

and

Observing wλ=0 on,by Lemmas 3.1 and 2.2,we see thatand soon eachfor all λ ∈ (λ0,r).That is

Suppose the contrary λ0> 0.We conclude that

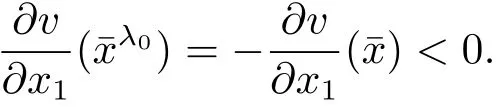
Set
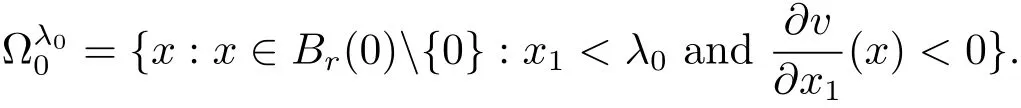
Let ?0be the symmetric set ofwith respect to the plane x1= λ0.Then ?0is an open set andis its interior point,and
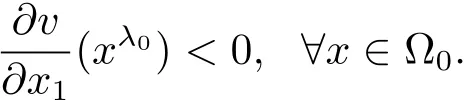
Recalling the definition of Iλ0(v)(x),we have,by the assumption λ0> 0,that
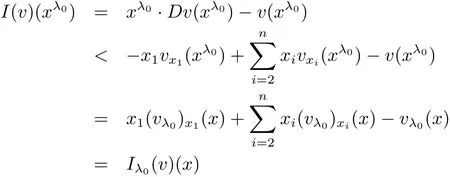
for all x∈?0.
Hence,(3.10)–(3.12)hold for λ = λ0and all x ∈ ?0,i.e.,

Using Lemmas 2.2 and 3.1,we obtain that wλ0≡0 in a ball Bδ()contained in ?0.Therefore v≡vλ0and so Lλ0(v)≡0 in Bδ(),contradicting(3.19).This proves(3.18).
With(3.18)in hands,we use Lemmas 2.2 and 3.1 again to obtain
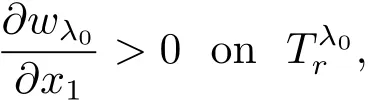
which implies
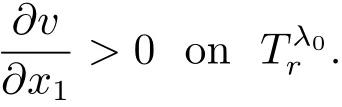
This and(3.18)mean λ0∈ Q,contradicting the definition of λ0.In this way,we have proved Claim 3.
Now we complete the proof of Theorem 1.1.Since λ0=0,by Claim 3 and(3.16),we have
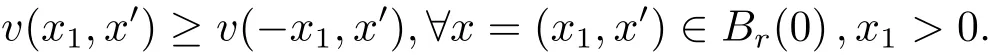
The opposite inequality is also true,because V(x):=v(?x1,x′)is a solution to(3.1)in Br(0){0}and the same conditions as v holds for V.This proves(3.5)and thus Theorem 1.1.

