Online Group Recommendation with Local Optimization

Haitao Zou , Yifan He, Shang Zheng, Hualong Yu and Chunlong Hu

1 Introduction

Recommendation technology is a popular and highly practical research topic. It provides reference about movies, products, restaurants and many other items by analyzing group perception data in a certain area. Collaborative recommender systems derive a list of recommended items by analyzing the similarity between users and predicting a user’s rating of an item based on similar users’ ratings of the same item. The classical recommendations are personalized, each user receives his own suggestions. However,there are some scenarios where a group of individuals participate in a single activity, such as watching a movie, or travel together, in which a group recommender suggestion is needed. Generally, the group recommendation should reflect a set of connected individuals’ preferences, which can be done by (i) analyzing a joint profile created by all users in the group [Yu, Zhou, Hao et al. (2006)] or (ii) collecting the recommendations of all members in the group into one recommender list [Gorla, Lathia, Robertson et al.(2013); Ntoutsi, Stefanidis, Kjetil et al. (2012)]. Nevertheless, the first method may bring bias towards those users with limited purchase records, while the second one is more flexible but its complexity directly depends on the number of individual users, which is extremely large considering the currentE-commerce data volume.

Our work in this paper follows the first approach solving the online group recommendation problem, because we argue that when utilizing the same kind of recommendation algorithms (such as matrix factorization based, or neighbourhood based collaborative filtering techniques), Using a joint profile of a group to derive the recommendation is faster than using individual user profile. Considering the circumstance in Fig. 1, the graph is divided into three groups. When using a joint profile to produce the group recommendation,its process only involves three profiles; meanwhile, using individual user profile to achieve the same task, it has to process 13 profiles (since identifying groups is a necessary procedure for both methods, the processing time of this part is not taken into account). And it is a general case that the number of groups is much smaller than the number of users in online social networks. The main challenge here is how to capture and eliminate the bias towards certain users. Through close study we find that, the bias is not mainly constructed by the one towards users with sparsest profile but users with limited or loose connections to the target group. The difference between these tow kinds of users is that,the profiles of users with limited connections to the target group are not necessarily sparse, they are just not in the core of the group; but users with sparest profile are always dangling or stay outside of the existed groups.

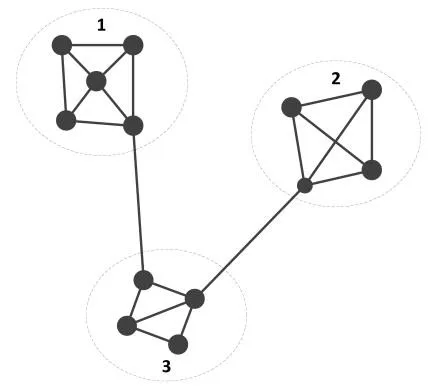
Figure 1: Group partition sample

In this work, we present a local optimization model for online group recommendation.This model spots the difference between each group members with the relevance of items to the group as a whole. In doing so, we show that higher quality and efficiency recommendations can be computed by eliminating the bias towards users at the edge of the online group through introducing jointly group profiles rather than merging individuals’ ranked recommendations. In summary, we make the following contributions:

(1) We introduce a local optimization model for group recommendation, unlike previous work which focuses on merging recommendations computed for individual users, we use sub-group profiles to compute the item relevance. Such method not only captures and removes the bias existed in the traditional group recommendation algorithms in a certain degree, but also shows an clear efficiency advantage comparing with some of the state-of-the-arts.

(2) We then use this model to derive a local-topology based framework for individual recommendation. We calculate the difference between users with their groups and use it to generate a personalized item list.

(3) We also propose an approach to overcome the problem caused by dynamic change or user updating about the network. We can detect the target user’s (when he is newly added, or changes his connections with other users) group by analyzing the link types between he and his neighbours, and then use the group information to generate his recommendations.

(4) We evaluate our group and single-user recommendation model alongside state-ofthe-art CF approaches on MovieLens datasets, and all the results sustain our claims that the proposed methods consistently generate the promising result.

The rest of the work is organized as follows: in Section 2, we introduce the preliminaries and the general process for single-user recommendation and group recommendation,respectively. Section 3 provides the fundamentals, theoretical and the main ideas about our algorithms. The experimental results are shown in Section 4. Related works are presented in Section 5, followed by conclusions in Section 6.

2 Preliminaries

In this work, we consider an online recommender system with a set of items I, and a set of users U. Each user u∈U can specify one (or no) rating on each item i∈I. Without loss of generality, let the domain of users’ ratings be the real values in [0,1], where 0 and 1 indicate total dislike and maximum appreciation, respectively. We use Ruto denote the rating vector of user u, and Ru,kis the rating from user u on item k. Obviously, the recommendation techniques are introduced to predict those blank entries in R, and they can be divided in to two kinds based on their recommender targets: single-user recommendations, and group recommendations.

2.1 Single-user recommendations

The recommendation strategies can be categorized into: (i) content filtering, that only relies on users’ past behaviors; (ii) collaborative filtering, that uses similar users’behaviors to recommend items; and (iii) hybrid, that combines (i) and (ii) together to generate recommendations. Our work is focused on collaborative filtering techniques,and we fall into the area of Latent Factor Models. The idea behind these models is to factorize the rating matrix R into two lower matrices u and ?, which minimizes the regularized squared error on the set of known ratings [Cheng, Yuan, Wang et al. (2014);Koren, Bell and Volinsky (2009)], the objective function is shown as (1):

Where u denotes the user factors and ? denotes the item factors, K is the rating set that Rijexists. Each user and item is represented over a fixed f-dimensional feature space.

Some of the popular latent factor models are based on Matrix Factorization (MF). In this work, we utilize this model to assist group recommendation.

2.2 Group recommendations

In most cases, recommender systems are dedicated to help individual users. Yet, there are still some situations in which items are chosen for a group of users. Furthermore, in a real life situation, the size of groups with highly similar members tend to be small, since they are family members or close friends. While, in a online social network, the size of groups with highly similar members will be larger due to the rapid development of internet,which makes the definition about group is close to the definition of community [Burton and Giraud-Carrier (2014); Chen, Zhu, Peng et al. (2014); Han and Tang (2015)]. In this work, we focus on online group recommendation, which can be achieved by two categories of approaches: (i) analyzing a joint profile created by all users in the group,and (ii) generating the recommendations of all users in the group, and then aggregating them into one recommender list.

Creating Group Profiles.Such method is very simple and straightforward, we borrow the description about this idea from Gorla et al. [Gorla, Lathia, Robertson et al. (2013)]:Suppose we have two users in the group. If they rated {i1,i2} and {i3,i4} respectively,their group profile is {i1,i2,i3,i4}; If their ratings is overlapped on certain items, such as{i1,i2} and {i2,i3}, then their group profile is {i1,mean(i2),i3}. This group profile can be treated as a individual user’s profile, and further used in any state-of-the-art collaborative filtering methods.

Aggregating Individual Recommender List.This kind of approach is a further processing about the single-user recommendation. When we generate recommender item lists for users of a group, the system selects an aggregating method (least misery design,fair design, ormost optimistic design), and sets relevance score for each item in the above mentioned lists.Then, a re-ordered group recommender list based on the relevance score is generated.

The first approach outperforms the second one in efficiency, but it may bring bias towards those users having limited connections with this group [Gorla, Lathia, Robertson et al. (2013)]. The second approach is more flexible, but its complexity directly depends on the number of individual users, which is extremely large considering the current E-commerce data volume [Ntoutsi, Stefanidis, Kjetil et al. (2012)]. In this work, we fuses both approaches by proposing a local optimizing group recommendation model in order to produce better online group recommender results. The key challenge is how to overcome their drawbacks but keep their advantages.

3 Local optimization for online group recommendation

As we mentioned in the previous section, our model has to solve the problems caused by the classic strategies, which are bias towards users with limited connections and high computational complexity.

3.1 Bias eliminating

This part of improvement is targeted at the approach which creates group profiles and uses it to recommend. A key aspect of such method that is missing is the notion of divergence among users in the group.

We consider an online user group topology as an undirected graph G(V,E), where each node in V is corresponding to a user in the group, and each edge in E represents the link that connected two group members. Then the group recommendation problem can be defined as:

Problem:Given a group G (V, E), how to find a set of itemsStoG, and satisfy

where Sjis the group preference rating on item j.

Generally, Sjcan be computed by the relevant collaborative filtering techniques where group file about G is created and treated as an individual user. However, when creating group profile to capture G’s preference, users in the group center have the same contributions as the users on the group edge, which causes such preference deviate from the right zone. The main problem here is how to correct the offset or how to avoid such situation. Further, the regulation of constructing G is varied based on its purpose. But basically, users in G share their preferences somehow, in most cases, either they are connected by preference similarity, or they are connected by social links. Hence, it is intuitive to classify the nodes ∈G into several sub-groups by their connectivities, so as to refine their contributions towards the final group recommender results.

The definition about connectivity between users is relevant with the criterion that we construct the group: If G is built on users’ preferences, the connectivity between two users can be measured by Pearson Correlation Coefficient; If G is modeled by social links,the connectivity between two users is measured by its Jaccard Similarity. Formally, we refer toas the neighbours of node v. Notation dvdenotes the number of nodes in. Then we have the following definition:

Definition (connectivity):Ifu∈G,v∈G, andev,u∈E, then the connectivity betweenu,vis denoted as:

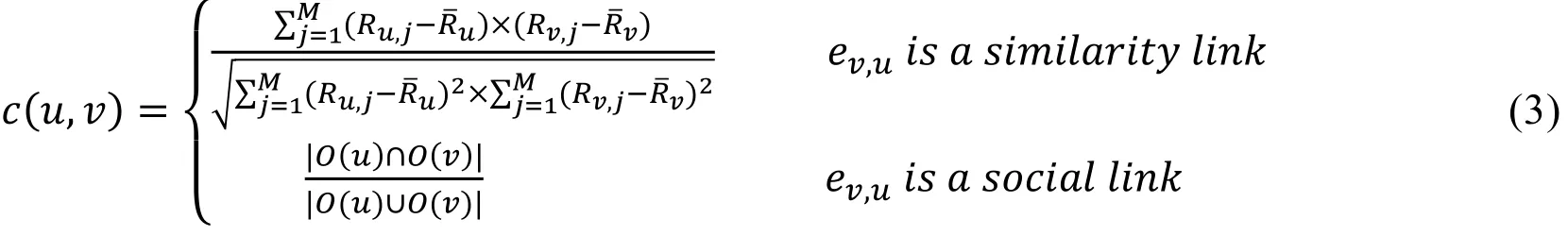
Suppose g1,… ,gmis the sub-groups of G which is derived from users’ connectivities,G’s corresponding sub-group recommender item sets are s1,…,smrespectively. Then, the original group recommendation problem can be transformed to satisfy (4):

where si,jis the preference rating of sub-group gion item j, and it can be computed with the same techniques as Sj.

Eq. (2) and Eq. (4) are not equivalent, since (4) is a local optimization process, while (2)is a global optimal solution. Generally, we have the following proposition.

Propersition:Given the online groupG (V,E), if we partitionGinto sub-groups byusers’ connectivity, the local optimization solution is better than the global one.

The advantages of using local optimization method come from several aspects. We first transform (2) as:

When group partition is ideal, S and giare orthogonal, which makesand helps to remove the redundant nodes. Moreover, the local optimal solution can assign weight to each sub-group according to their contributions toward G,and it is more suitable and robust for dynamic systems and achieves better real-time performance.

3.2 Computational complexity reducing

In order to achieve better performance about computational complexity, our processing steps is shown as:

(i) Partition G into g1,… ,gmby users’ connectivities in G. We can apply classification algorithms (such as SVM, ELM, etc.) here or just divide G by setting the sub-group size manually.

(ii) Create sub-group profile for each sub-group, which is very similar to the process about creating group profiles: If users u and v rated {i1,i2} and {i3,i4} respectively(u,v∈gk), their sub-group profile for gkis {i1,i2,i3,i4}; If their ratings is overlapped on certain items, such as i1,i2and i2,i3, their sub-group profile for gkis{i1,mean(i2),i3}.

(iii) Treat each sub-group profile as an individual user’s profile, and use MF methods to estimate the sub-group preference ratings.

(iv) Aggregate sub-group recommender list. We choose theleast miserystrategy, since Baltrunas et al. [Baltrunas, Makcinskas and Ricci (2010)] concludes that such strategy outperforms a range of other techniques.

One may notice that, our method is very flexible. When the number of sub-groups is small enough, it can shrink into one large group, which is G, then it is corresponding to the classic approach using group profile to recommend. When the number of sub-groups is large enough, it can be equal to |G|, then it is corresponding to the approach that aggregates individual recommender list as group recommendation.

Unfortunately, introducing sub-groups may still affect the precision of the prediction on group preference ratings. When we utilize MF techniques to implement step (iii), the traditional methods try to optimize (1). Conceptually, minimizing the difference between the real ratings and the estimated ratings can be viewed as a self-calibration process.However, the solution space of the optimization problem could be large, especially when we treat sub-group profiles as individual user profiles, which makes the user-item matrix sparser, and might result in a biased estimator for uiand ?j. Thus, we introduce the highorder distance principle [Xu, Yao, Tong et al. (2017)] which aims to minimize not only the difference between the estimated and real ratings of the same (user, item) pair, but also the difference between the estimated and real rating difference of the same user across different items (i.e. the second-order rating distance). The optimization function is shown in (6):

where λdis the parameter to control the effect of the second-order rating distance.σ(x,y)=1/(1+e?(x?y)), and Iij,i′j′=1 if ratings Rijand Ri′j′exist with

3.3 Single-user recommendation estimation

Since we treat each sub-group profile as individual user profile, it is convenient to estimate single-user predictive ratings on items by utilizing collaborative filtering algorithms, and generate a recommender item list based on this rating for a target user.The intuition of this idea is that users’ preferences on items construct the group preference, and therefore, group preference on items helps to derive users’ preferences.Further, the group G is partitioned into sub-groups, which have different affects on predictive ratings: The sub-group that the target user is belong to affects more than the one that target user is not. Hence, each sub-group should be assigned different weights.The predictive rating from user u on item j is computed as:

whereand siis gi’s sub-group profile.andare the average ratings for u and sirespectively, c(u,si) is computed with (3) as eu,siis a similarity link.Moreover, user u may belongs to several groups due to his disperse preference or different purpose on organizing user groups. Our computation about his predictive ratings should take this circumstance into account. Fortunately, Eq. (7) can be easily extended by considering all the groups where u is belong to, and using all the sub-groups constructed the corresponding group to implement the estimation about predictive ratings on items.Such extension not only utilizes more information to achieve better prediction on item ratings, but also satisfies the requirement of users’ diverse interests. Since the number of sub-groups is much smaller than the number of users, our method decreases the computation complexity comparing with the traditional collaborative filtering process.

3.4 Single-user recommendation dynamic updating

The traditional method to handle the dynamic change is to provide a periodic analysis of the network to achieve this purpose. Such process not only needs much more time, it also lacks flexibility to reflect a user’s current state. Therefore, we propose a local topology based approach, which only evolves the neighbors of the target user (node), to determine which new groups he is belong to, and then use those groups’ information to estimate the predictive ratings for him by (7).

The idea of our approach is to identify the relationships between the target user and the groups that he is connected with. Take Fig. 2 as an example, user v can be either belong to G, or not belong to G. It is intuitive to derive the result by considering the edges that v links to G (or the subset of G). Our previous work [Zou, Gong and Hu (2016)] proposes a claim, which is used to determine whether a target node belongs to a community or not.The concept of a “community” in a (web, social, or informative) network is understood as a set of individuals that are very similar, or close to each other, more than to anybody else outside the community. Meanwhile, the concept “group” we discussed in this work is built by similarity links or social links. Therefore, we can introduce this claim to determine the target user belongs to a certain group or not.

Figure 2: Examples that shows different partitions between v and U

Formally, our claim is stated as:

Claim:Given groupG(V,E), suppose={u1,…,uk}? G,?v ∈ V, if

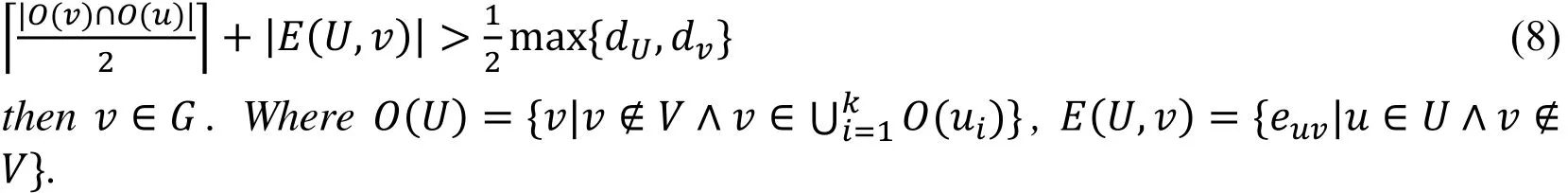
The proof about this claim can be learned from Zou et al. [Zou, Gong and Hu (2016)].With this claim, for a given node who changes his local topology of his network (or newly added into this network), if he and a well-clustered set of nodes have enough common neighbors, we can deterministically say that this node belongs to the same group as that set of nodes. And we can generate a recommender item list for him ordered by the predictive ratings using the group information he is part of.

4 Experiments

We implement all the experiments on a PC with quad-core CPU (Intel i5, 3.3 GHZ), 8.0 GB main memory and 1 T hard disk, running Microsoft Windows 7 Edition, and perform the relevant algorithms on three available MovieLens datasets2https://grouplens.org/datasets/movielens/(which differ in sizes)during the experiments: MovieLens 1M (labeled as ML1M) contains 1 million ratings from 6000 users on 4000 movies; MovieLens 10M (labeled as ML10M) contains 10 million ratings, 100,000 tag applications applied to 10,000 movies by 72,000 users;MovieLens 20M (labeled as ML20M) contains 20 million ratings, 465,000 tag applications applied to 27,000 movies by 138,000 users.

The distribution of users on the number of rated movies in these datasets is shown in Fig.3. We can see that users with small number of rated movies take a large proportion in user distribution. Although previous researches have used the MovieLens data to examine group recommendation scenarios, these datasets do not include any explicit group membership data. We reference process in Baltrunas et al. [Baltrunas, Makcinskas and Ricci (2010)] and overcome this problem. Since our approaches are focused on online group recommendation, which is mainly about the users with common tastes, we group users with high inner similarities.

Figure 3: Item distribution over the number of users on Movielens

During the experiments, we randomly divided each user’s purchase record in the datasets by 60% for training and 40% for testing, and repeat this process 10 times and generate average testing results for their corresponding measurements. We set the dimensional feature number f=40, and the iteration times to be 80 for our algorithms when introducing MF method to generate group recommendation.

4.1 Methodology and metrics

The goals of our evaluations are addressing three questions: 1) How do our approaches perform for group recommendation and single-user recommendation, respectively? 2)What is the performance improvement with complexity reducing? 3) How effective can our algorithms achieve? We select two kinds of metrics to evaluate the relevant performance.

Metrics for Group Recommendation.We measure the normalized Discounted Cumulative Gain (nDCG), which is used to measure the goodness of ranked list by considering the item ratings with Discounted Cumulative Gain (DCG). Suppose j1,…,jlis a ranked list of items recommended to the target group, the DCG for user u at rank k and the nDCG are computed as:

Whereis the maximum possible gain value for user u that is obtained with the optimal re-order of thekitems in j1,…,jl.

Metrics for Single-User Recommendation.We use Mean Absolute Error (MAE) and Standard Deviation of MAE (SDM) to measure the accuracy of the predictive ratings.MAE and SDM are computed as:

4.2 How many sub-groups should be divided

Since our method would divide the target group into sub-groups, if the target group size is too small, which is discussed in Baltrunas et al. [Baltrunas, Makcinskas and Ricci(2010)], it is not consistent with the online group status, and makes our method similar to those approaches aggregating individual recommender list. Therefore, we set the group size to be 50, and investigate the balance between the number of sub-groups and the algorithms’ precision.

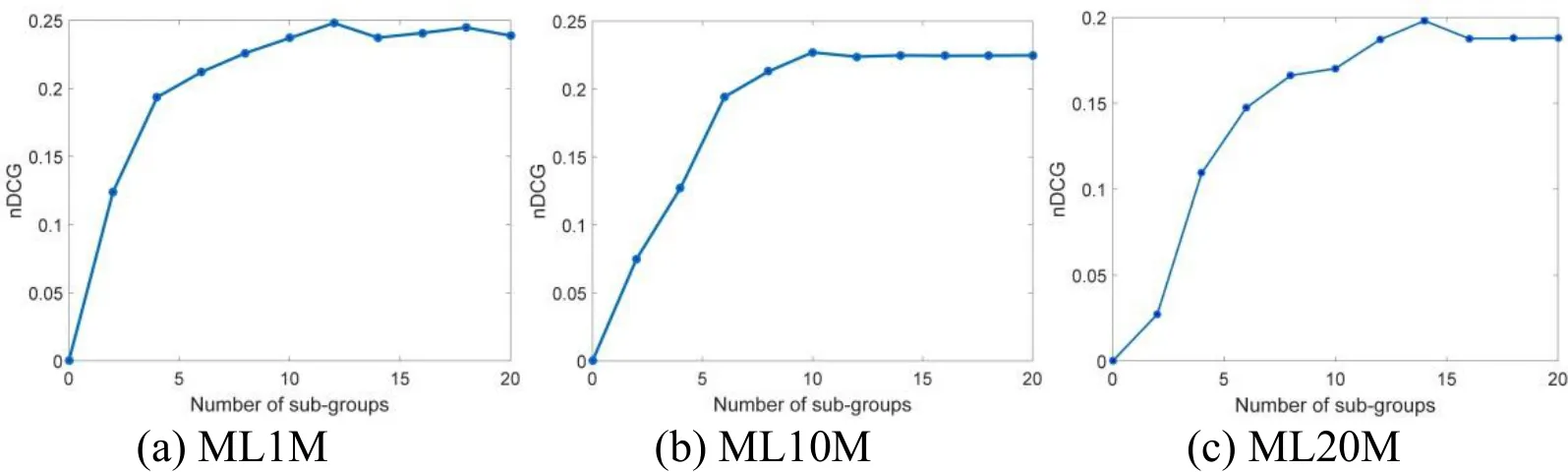
Figure 4: nDCG variation over the number of sub-groups on MovieLens

Fig. 4 shows the number of subgroups and their corresponding nDCG that our algorithm achieves. We can see that, the more sub-groups we divided, the better nDCG our method will perform, and nDCG increases gently when the number of sub-groups reaches a certain number: on ML1M, this number is 12; on ML10M, this number is 10; on ML20M,this number is 14. We set the number of sub-groups is 12, 10, and 14 for each dataset respectively by default.

4.3 Performance of group recommendation

During the experiments about the group recommendation, we compute nDCG over all the users in any group with the similar method as in Baltrunas et al. [Baltrunas, Makcinskas and Ricci (2010)], and test the time consuming about the relevant methods. We choose the Information Matching Model (IMM) introduced in Gorla et al. [Gorla, Lathia,Robertson et al. (2013)] for comparison. We name our local optimization method as LOM, which is only utilizing bias eliminating process, and further name our method LOM+CCR, which is the advanced model with bias eliminating and computational complexity reducing. The results are shown in Tab. 1.

We can see that IMM performs a little better than LOM and LOM+CRR, and LOM+CRR is better than LOM when considering nDCG, which means aggregating individual recommender list may utilize more useful information than merging group profiles, and using the high-order distance principle to enhance the precision about group recommendation is more accurate. When comparing the efficiency, IMM and LOM+CRR are much slower than LOM. IMM is better than LOM+CRR in ML10M and ML20M,and LOM+CRR is better than IMM in ML1M. The reason why LOM+CRR is slower is that, LOM+CRR brings further computation about the real rating difference of the same user across different items, which may harm the efficiency in a certain degree.

In conclusion, although LOM and LOM+CCR are not better than IMM in nDCG, LOM extraordinarily outperforms IMM in efficiency.

Table 1: Group recommendation performance results

4.4 Performance of single-user recommendation

When testing the performance of single-user recommendation, we choose MF [Koren,Bell and Volinsky (2009)] as the classical method, and HoORaYs [Xu, Yao, Tong et al.(2017)] as the state-of-the-art for comparison. We still use LOM and LOM+CRR to denote the methods for our individual recommendation approaches respectively. The results are shown in Tab. 2.

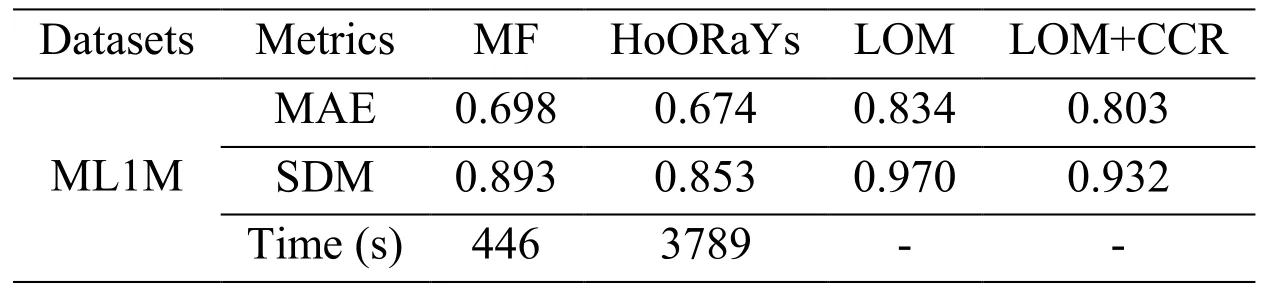
Table 2: Single-user recommendation performance results

MAE 0.633 0.623 0.811 0.784 ML10M SDM 0.831 0.802 0.911 0.885 Time (s) 4553 59073 - -MAE 0.617 0.629 0.800 0.774 ML20M SDM 0.815 0.812 0.889 0.891 Time (s) 8224 119611 - -

Generally, if we sort the algorithms used for comparison by their accuracy about the predictive ratings, we have HoORaYs, MF, LOM+CCR, and LOM. Since HoORaYs and MF are introduced directly for individual recommendations, their design is more suitable for computing the predictive ratings. And HoORaYs minimizes not only the difference between the estimated and real ratings of the same (user, item) pair, but also the difference between the estimated and real rating difference of the same user across different items, it is more accurate than MF, which is the similar reason why LOM+CCR is more accurate than LOM. Further, the average similarity among each group is no more than 0.30, when using such group information to estimate single-user predictive ratings(LOM and LOM+CCR) will bring much noise. We speculate that, if the groups are well organized (the inner group similarity is higher), our LOM and LOM+CCR would perform better. Meanwhile, if we sort the algorithms used for comparison by their efficiency, we have LOM, LOM+CCR, MF, and HoORaYs. And the HoORaYs is much slower than all the other algorithms. This is due to the extra calculation about the secondorder rating distance, which is the similar reason for LOM+CCR is slower than LOM.Since LOM, LOM+CCR are not designed for personal recommendation directly, their time consuming is relevant with the results about group recommendation, and based on the previous results, their efficiency is better than HoORaYs and MF.

In summary, LOM and LOM+CCR are less accurate than MF and HoORaYs, but when processing large data volume in E-commerce systems, they may save much time.

5 Related works

The researchers have conducted a wide range of research about recommendations, such as recommending products [Zhang, Zheng, Yuan et al. (2015); Zou, Gong, Zhang et al.(2014)], POI [Guo and Gong (2016); Zhang, Zheng, Yuan et al. (2015)], texts [He, Chen,Kan et al. (2015); Moghaddam and Ester (2011)], etc. These works are very different from the technical level, but the main ideas are basically the same: They use the most relevant data dimension (for example, purchase records for product recommendations;geographic latitude for POI recommendations; textual data for text recommendations) as key attribute, and combine with other dimensions such as social network topology, time,locations (or the above-mentioned data dimensions cross-assistance) as auxiliary information, to provide recommendations for individuals.

Recently, several works have been focused on group recommendations which can be classified into two kinds. The first kind provides the group recommendations by introducing a joint profile created by all users belong to this group. The second kind aggregates the recommendations of all users in the group into a single recommendation list. Some works select the second method since it is more flexible and offers opportunities for improvements in terms of efficiency [Ntoutsi, Stefanidis, Kjetil et al.(2012)]. For example, Gorla et al. [Gorla, Lathia, Robertson et al. (2013)] presents a probabilistic group recommendation framework for movies based on the notion of information matching. This model defines group relevance as a combination of the item’s relevance to each user as an individual and as a member of the group. Quintarelli et al.[Quintarelli, Rabosio and Tanca (2016)] proposes a new-items sensitive model and determines the preference of an ephemeral group by combining the preferences of the group members on the basis of their contextual influence. Kotsogiannis et al.[Kotsogiannis, Zheleva and Machanavajjhala (2017)] considers the problem of directed edge recommendations where the system recommends the best item that a user can gift,share or recommend to another user that he is connected to, which utilizes the preferences of both the sender and the recipient by integrating individual user preference models into the recommendation process. Besides, there are many research works which are devoted to optimization strategy, such as package fairness [Serbos, Qi, Mamoulis et al. (2017)],group satisfaction [Roy, Lakshmanan and Liu (2015)], etc.

However, the computational complexity of all the above mentioned group recommendation models directly depends on the number of individual users, which makes their efficiencies questionable when taking today’s online data scale into account. In this work, we design a local optimization approach which focuses on the sub-group profiles to compute the item relevance. Since such computation scale grows linearly with the number of groups instead of the number of users, it can be accomplished efficiently. We also provide a local-topology based updating strategy by analyzing the link types between user and his neighbours when the topology of user network changes or increases, the time demand is also linear.

6 Conclusions

Recent research about group recommendation is usually designed to aggregate individual recommender list or create group profiles for further computing. These methods either strongly limited by their application environment, or bring bias towards those users having limited connections with this group. In this work, we propose a local optimizing approach for group recommendation, which eliminates bias, and reduces computational complexity in a certain degree. Our approach may also derive single-user recommendation, and overcome the problem caused by dynamic change or user updating about the network.Experimental analysis on three different MovieLens datasets shows that, our LOM and LOM+CCR generally outperform several state-of-the-arts in efficiency. And we also provide the explanations behind the phenomena during the experiments.

Acknowledgement:This research was financially supported by the High Level Talents Scientific Research Fund in Jiangsu University of Science and Technology under grants 1132921506 and Jiangsu natural science foundation under grants BK20150471. Any opinions, findings, conclusions, and/or recommendations expressed in this material,either expressed or implied, are those of the authors and do not necessarily reflect the views of the sponsors listed above.

Baltrunas, L.; Makcinskas, T.; Ricci, F.(2010): Group recommendations with rank aggregation and collaborative filtering.ACM Conference on Recommender Systems, pp.119-126.

Burton, S. H.; Giraud-Carrier, C. G. (2014): Discovering social circles in directed graphs.ACM Transactions on Knowledge Discovery from Data,vol. 8, pp. 1-27.

Chen, Y.; Zhu, W.; Peng, W.; Lee, W. C.; Lee, S. Y. (2014): CIM: Community-based influence maximization in social networks.ACM Transactions on Intelligent Systems &Technology,vol. 5, pp. 25.

Cheng, J.; Yuan, T.; Wang, J.; Lu, H.(2014): Group latent factor model for recommendation with multiple user behaviors.International ACM SIGIR Conference on Research & Development in Information Retrieval, pp. 995-998.

Gorla, J.; Lathia, N.; Robertson, S.; Wang, J. (2013): Probabilistic group recommendation via information matching.Proceedings of the 22nd International Conference on World Wide,vol. 4, pp. 495-504.

Guo, J.; Gong, Z.(2016): A nonparametric model for event discovery in the geospatialtemporal space.ACM International on Conference on Information and Knowledge Management, pp. 499-508.

Han, Y.; Tang, J. (2015): Probabilistic community and role model for social networks.Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 407-416.

He, X.; Chen, T.; Kan, M. Y.; Chen, X.(2015): TriRank: review-aware explainable recommendation by modeling aspects.ACM International Conference on Information and Knowledge Management, pp. 1661-1670.

Koren, Y.; Bell, R.; Volinsky, C. (2009): Matrix factorization techniques for recommender systems.Computer,vol. 42, pp. 30-37.

Kotsogiannis, I.; Zheleva, E.; Machanavajjhala, A.(2017): Directed edge recommender system.Tenth ACM International Conference on Web Search and Data Mining, pp. 525-533.

Moghaddam, S.; Ester, M. (2011): ILDA: Interdependent LDA model for learning latent aspects and their ratings from online product reviews.Proceedings of the 34th international ACM SIGIR conference on Research and development in Information Retrieval, pp. 665-674.

Ntoutsi, E.; Stefanidis, K.; Kjetil, G.; Kriegel, H. P. (2012):Fast group recommendations by applying user clustering. Springer Berlin Heidelberg.

Quintarelli, E.; Rabosio, E.; Tanca, L.(2016): Recommending new items to ephemeral groups using contextual user influence.ACM Conference on Recommender Systems, pp.285-292.

Roy, S. B.; Lakshmanan, L. V. S.; Liu, R.(2015): From group recommendations to group formation.ACM SIGMOD International Conference on Management of Data, pp.1603-1616.

Serbos, D.; Qi, S.; Mamoulis, N.; Pitoura, E.; Tsaparas, P.(2017): Fairness in package-to-group recommendations.International Conference, pp. 371-379.

Xu, J.; Yao, Y.; Tong, H.; Tao, X.; Lu, J.(2017): HoORaYs: High-order optimization of rating distance for recommender systems.ACM SIGKDD International Conference, pp.525-534.

Yu, Z.; Zhou, X.; Hao, Y.; Gu, J. (2006): TV program recommendation for multiple viewers based on user profile merging.User Modeling and User-Adapted Interaction,vol.16, pp. 63-82.

Zhang, F.; Zheng, K.; Yuan, N. J.; Xie, X.; Chen, E. et al.(2015): A novelty-seeking based dining recommender system.International Conference on World Wide Web, pp.1362-1372.

Zou, H.; Gong, Z.; Hu, W. (2016): Identifying diverse reviews about products.World Wide Web-internet & Web Information Systems,vol. 20, pp. 1-19.

Zou, H.; Gong, Z.; Zhang, N.; Li, Q.; Rao, Y. (2014): Adaptive ensemble with trust networks and collaborative recommendations.Knowledge & Information Systems,vol. 44,pp. 1-26.