Coherence migration in high-dimensional bipartite systems
Zhi-Yong Ding(丁智勇) Pan-Feng Zhou(周攀峰) Xiao-Gang Fan(范小剛)Cheng-Cheng Liu(劉程程) Juan He(何娟) and Liu Ye(葉柳)
1School of Physics and Electronic Engineering,Fuyang Normal University,Fuyang 236037,China
2Key Laboratory of Functional Materials and Devices for Informatics of Anhui Educational Institutions,Fuyang Normal University,Fuyang 236037,China
3School of Physics and Optoelectronics Engineering,Anhui University,Hefei 230039,China
Keywords: first-order coherence,mutual correlation,coherence migration,high-dimensional
1. Introduction
Coherence, being an inevitable consequence of the superposition principle, is one of the most important concepts in quantum optics research, which can be used to describe the interference capability of interacting fields and the characteristics of photon stream.[1–5]It even plays an important role in some interdisciplinary fields, such as quantum thermodynamics,[6–8]quantum metrology,[9–11]and quantum biology.[12–14]To quantify coherence of a quantum state,many measurements have been proposed from different perspectives. Some are based on quantum optical methods,[15,16]and others are based on the viewpoints of resource theory.[17–20]Although coherence is usually considered to be the characteristics of the whole physical system, we need to investigate the internal distribution of coherence between subsystems and their correlations for predicting coherence evolution (migration). For a composite quantum state, coherence between subsystems can be looked as its ability to create entanglement.[21,22]Therefore,it is of great significance to explore the rule of coherence migration for a bipartite composite system.
In 2015, Svozil′?ket al. proposed a conservation law between the first-order coherence and mutual correlation for arbitrary bipartite qubit states under global unitary transformations. They analyzed the characteristics of coherence migration and introduced two unitary operators for obtaining minimum or maximum first-order coherence for a given bipartite qubit state.[15]Meanwhile, Geet al.studied coherence migration and conservation relation of nonclassicality and entanglement for Gaussian states in a beam splitter.[23]Especially,ˇCernochet al.demonstrated the theory of coherence migration through two interesting experimental schemes,among which,one is based on linear optical controlled-phase quantum gate and the other employs nonlinear optical process.[24]Despite the inspiring success in theory and experiment, the conservation law for coherence and correlation are carried out only for a bipartite qubit state.It is then natural to question whether there is a more general conclusion for high-dimensional bipartite composite state. Inspired by the aforementioned research,we consider such a problem in this paper. We firstly construct an extended Bloch decomposition form of an arbitrary (m ?n)-dimensional bipartite composite state,and then generalize the concepts such as first-order coherence, mean coherence, mutual correlation and the conservation law to an arbitrary highdimensional system. Meanwhile, coherence migration under global unitary transformations in high-dimensional systems is investigated, and two kinds of unitary operators are generalized. We also show through explicit examples its capacity for obtaining the maximum and minimum first-order coherence.
On the other hand,the evolution of quantum states in open systems is an important research content of quantum information science.[25]It goes without saying that the inescapable interaction between a quantum system and its surrounding environment may lead to decoherence.[26–31]A popular method to investigate the dynamics of an open quantum system is to regard the principal system and the interacting environment as a larger composite closed quantum state,whose evolution can be described by a unitary transformation.[25]Here, this composite state is called as system-environment bipartite composite state. In general, the dimensions of the principal system and the environment are not the same. With assuming that the dimension of the system isd, the environment can be modeled in a Hilbert space of no more thann(n ≤d2)dimensions.Therefore,the system-environment state can be regarded as a typical (d ?n)-dimensional bipartite composite state. In this work,we explore the coherence migration of an arbitrary qubit system in a depolarizing channel in detail. The results show that the reduced first-order coherence of the principal system over time is transformed into mutual correlation of the systemenvironment bipartite composite state.The study of coherence migration in high-dimensional systems helps us not only understand the characteristics of first-order coherence and mutual correlation from the perspective of resource theory, but also design different schemes to enhance or weaken coherence. It is worth mentioning that our results might present a new mind of manipulating coherence and quantum correlation.
2. Conservation law of coherence and correlation in high-dimensional bipartite systems
The qubit is a fundamental concept of quantum computation and quantum information. Any single qubit state can be graphically represented by the Bloch vector.[25]If we extend the concept of qubit from two dimensions to finite dimensions,we use qudit to represent a quantum state ind-dimensional Hilbert space. In this section, we first review the decomposition form of a qudit state,and propose an extended Bloch representation for any (m ?n)-dimensional bipartite composite state. Then,we generalize the framework of first-order coherence, mean coherence, mutual correlation, and conservation law for coherence and correlation.
2.1. High-dimensional bipartite composite state
An arbitrary single qudit state in the finited-dimensional Hilbert space can be decomposed as[32]


where Im(n)is them×m(n×n) identity matrix,x{x1,x2,...,xm2-1}andy{y1,y2,...,yn2-1}are the corresponding extended Bloch vector of subsystems A and B withxi=Tr(ρABλi ?In),yj=Tr(ρABIm ?λj), andTis the correlation tensor of composite system withtij=Tr(ρABλi ?λj).
2.2. Conservation law for coherence and correlation
For a(m ?n)-dimensional bipartite composite stateρAB,as shown in Eq.(3),composed of subsystems A and B,we can calculate the reduced matrices of each subsystem as a partial trace, i.e.,ρA=TrB(ρAB)andρB=TrA(ρAB). By promoting the definition of Ref.[15],the degree of first-order coherence of each subsystem can be written as

On the other hand,we also generalize the definition of the mutual correlation between the two high-dimensional subsystems in Ref.[24]as

whereP=Tr(ρ2AB) is the purity of the high-dimensional bipartite composite state. We know that if the evolution of the composite state is unitary transformation, the purity will remain unchanged. That indicates when the mean coherence decreases (increases), the mutual correlation increases (decreases). We refer to the change of coherence between subsystems in this process as coherence migration.
3. Coherence migration under global unitary transformations
For simplicity, we assume that the dimensions of the two subsystems of the bipartite composite system are consistent. Now the research objectρABis limited to an arbitrary bipartite state in a composite Hilbert space?A??Bwith dim?A=dim?B=d. We know that the dynamics of a closed quantum system are described by a unitary transformation, which does not change the purity of the system. Therefore,if the global unitary operator acting on the quantum stateρABis represented byU, the evolution state can be expressed asρ′AB=UρABU?.
3.1. Maximum first-order coherence


Figs.1(a)and 1(b). In these figures,the dashed lines and solid lines represent the value of the original state and evolutionary state by the global unitary operation,respectively.The gray areas represent allowable values achievable by arbitrary global unitary transformations. We prepare 80000 random unitary operators by numerical simulation,and each gray point in the figures represents the evolution state after a possible unitary transformation.

Fig. 1. The (a) mean coherence and (b) mutual correlation as a function of parameter p of the isotropic state. Purple dashed line and brown dashed line depict the values of the mean coherence and the mutual correlation of the original state. The maximum of mean coherence and the minimum of mutual correlation are marked by purple solid line and brown solid line,respectively.The gray areas represent allowable values achievable by arbitrary global unitary transformations.
3.2. Minimum first-order coherence

In (3?3)-dimensional composite Hilbert space, the 9 mutually orthogonal maximally entangled states can be given as[36]
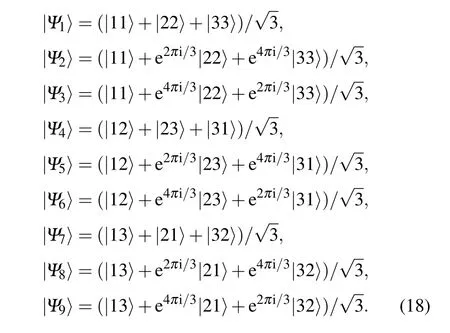

4. Coherence migration in open quantum systems
The dynamics of open quantum systems studies the interaction between the quantum system and its surrounding environment. A common method to investigate the dynamics of an open quantum system is to regard the principal system and the interacting environment as a larger composite closed quantum state,whose evolution can be described by a unitary transform.[25]Suppose we have a principal quantum systemρSind-dimensional Hilbert space, which is subjected to a dynamical evolution. Meanwhile, we assume that{|iE〉}ni=1is an orthonormal basis for the state space of environment,which can be modeled in a Hilbert space of no more thann(n ≤d2) dimensions. There is no loss of generality in assuming that the environment starts in a pure state. So thatρE=|1E〉〈1E|represents the initial state of interacting environment. The system-environment bipartite composite state is a typical(d ?n)-dimensional product stateρSE=ρS?|1E〉〈1E|.Assume that the global unitary operator acting on the composite state is denoted byU,whose specific form depends on the actual physical situation and system-environment interaction. Then the evolution state of the principal system can be obtained by performing a partial trace over the environment,
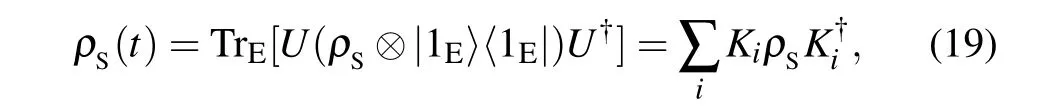
whereKi ≡〈iE|U|iE〉is customarily known as the Kraus operator on the state space of the principal system,which satisfies a normalization condition ∑i K?i Ki=I. Further,we can easily obtain the evolution state of the environment and the composite state,

where the probabilityp= 1-e-γ0tcan be considered as a time-dependent parameter to describe the strength of channel noise, andγ0is the corresponding decay factor. Therefore,we should assume that the environment is 4-dimensional,and{|1E〉,|2E〉,|3E〉,|4E〉}is an orthonormal basis for the state space of the environment. The system-environment stateρSE=ρS?|1E〉〈1E|is a(2?4)-dimensional bipartite composite state.
By use of Eqs.(19)and(20),we can calculate the evolution states of principal system and environment as

From the the above equations, we can find that the firstorder coherence of the principal systemD2S(t)decreases from the initial|r|2to 0, while the first-order coherence of the environmentD2E(t)decreases from 3 to|r|2with the increase of time. Therefore,the mean coherenceD(t)also monotonically decreases from the initial(3+|r|2)/8 to|r|2/8. Meanwhile,the mutual correlationT(t)increases monotonously from the initial(1+3|r|2)/8 to(4+3|r|2)/8. Note that we regard the principal system and the interacting environment as a larger composite closed quantum state, hence, the evolution of the open quantum system can be described by a unitary transform.Therefore, the conservation law for mean coherence and mutual correlation is still satisfied,i.e.,D+T=P=(1+|r|2)/2.It means that with the evolution of time,the reduced mean coherence is all transferred to the mutual correlation of the composite state.
Assume that the initial principal system is a general single qubit state withρS=r{0.7,0.5,0.4}. The coherence as a function of time-dependent parameterγ0tunder the depolarizing channel is shown in Figs. 2(a) and 2(b). As can be seen from Fig. 2(a), with the passage of time, the first-order coherence of the principal system gradually decreases from the initial 0.9 to 0, while the first-order coherence of the environment gradually decreases from the initial 3 to 0.9. We notice from Figs.2(a)and 2(b),although the first-order coherence of the environment may exceed 1, the mean coherence and mutual correlation of the open quantum systems are always within the range of[0,1]. The changes of coherence and correlation are completely symmetrical,and the center of symmetry isP/2=0.475.

Fig.2. (a)The first order coherence of the principal system(red line)and environment(blue line), (b)the mean coherence (purple line), and the mutual correlation(green line)as a function of time-dependent parameter γ0t under the depolarizing channel(assume the initial state is ρS =r{0.7,0.5,0.4}).
5. Summary and discussion
In summary, we have generalized the framework of the conservation law for first-order coherence and mutual correlation to an arbitrary(m?n)-dimensional bipartite composite state by introducing an extended Bloch decomposition form of the state. Then, we investigate coherence migration under global unitary transformations in high-dimensional systems,and generalize two kinds of unitary operators,which can help us obtain the maximum or minimum first-order coherence when they act on the quantum states. Moreover, we take depolarizing channels as a typical example to discuss coherent migration in open systems.
It is worth discussing that in order to describe the nonclassical correlation of bipartite composite systems, we generalize the definition of the mutual correlation between the two subsystems in Ref. [24] as Eq. (6). The research on the nonclassical correlation of bipartite composite systems is not only that, but also the violation of the CHSH inequality,[21]the discord,[37]the intrinsic concurrence,[39]the nonlocal advantage of quantum coherence,[39–41]and so on. These nonclassical correlations can be regarded as a useful quantum resource.[42]It is still an open problem to study the transformation of coherent and other quantum resources in highdimensional systems. We expect that our paper would present a useful idea to regulate the quantum resource for quantum information processing.
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant No.11605028),Anhui Provincial Natural Science Foundation, China (Grant Nos. 2108085MA18 and 2008085QA47), the Natural Science Research Project of Education Department of Anhui Province of China (Grant Nos. KJ2020A0527, KJ2021ZD0071 and KJ2021A0678),the Key Program of Excellent Youth Talent Project of the Education Department of Anhui Province of China (Grant No.gxyqZD2019042),and the Research Center for Quantum Information Technology of Fuyang Normal University(Grant No.kytd201706).
Appendix A



- Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes