ON A NEW NONTRIVIAL ELEMENT INVOLVING THE THIRD PERIODICITY γ-FAMILY IN π?S

WANG Yu-yu,WANG Jian-bo

(1.School of Mathematics and Science,Tianjin Normal University,Tianjin 300387,China)

(2.Department of Mathematics,School of Science,Tianjin University,Tianjin 300072,China)

ON A NEW NONTRIVIAL ELEMENT INVOLVING THE THIRD PERIODICITY γ-FAMILY IN π?S

WANG Yu-yu1,WANG Jian-bo2

(1.School of Mathematics and Science,Tianjin Normal University,Tianjin 300387,China)

(2.Department of Mathematics,School of Science,Tianjin University,Tianjin 300072,China)

In this paper,we discuss stable homotopy groups of spheres.By making a nontrivial secondary dif f erential as geometric input in the Adams spectral sequence,the convergence of h0gn(n＞3)in π?S is given.Furthermore,by the knowledge of Yoneda products,a new nontrivial element in π?S is detected.The scale of the nontrivial elements is expanded by our results.

stable homotopy groups of spheres;Toda-Smith spectrum;Adams spectral sequence;May spectral sequence;Adams dif f erential

1 Introduction

Let S denote the sphere spectrum localized at p and p denote an odd prime.From [14],the homotopy group of n-dimensional sphere(r＞0)is a fi nite group.So the determination ofhas become one of the central problems in algebraic topology.

Ever since the introduction of the Adams spectral sequence(ASS)in the late 1950’s(see [1]),the study of the homotopy groups of spheres π?S was split into algebraic and geometric problems,including the computation ofand the detection which element ofcan survive to,here A is the mod p Steenrod algebra,is the E2-term of the ASS.By[2],

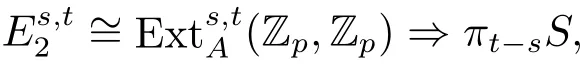
and the Adams dif f erential is

In addition,we also have the Adams-Novikov spectral sequence(ANSS)[12,13]based on the Brown-Peterson spectrum BP in the determination of π?S.

Many wonderful results were obtained,however,it is still far from the total determination of π?S.After the detection ofS for p=2,j 6=2,by Mahowald in[11],which was represented bymany nontrivial elements in π?S were found.Please see references[5-9]for details.In recent years,the fi rst author established several convergence of elements by an arithmatic method,see[16-18,21].

In[5],Cohen made the nontrivial secondary Adams di ff erential d2(hi)=a0bi-1(p＞2,i＞0)as geometric input,then,a nontrivial element ξi∈π(pi+1+1)qS(i≥0)is detected. In this paper,we also detect a new family in π?S by geometric method,the only geometric input used in the proof is the secondary nontrivial di ff erential given in[20].

The main result is obtained as follows.

Theorem 1.1Let 3≤s＜p-1,n＞3,p≥7,then

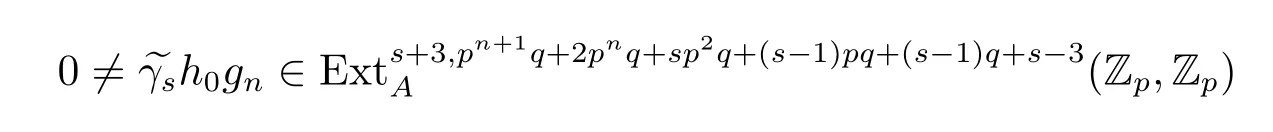
is a permanent cycle in the Adams spectral sequence and converges to a nontrivial element of order p in

The paper is organized as follows.After giving some necessary preliminaries and useful knowledge about the MSS in Section 2.The proof of Theorem 1.1 and some results on Ext groups will be given in Section 3.

2 Related Spectrum and the May Spectral Sequence

For the convenience of the reader,let us brief l y indicate the necessary preliminaries in the proof of the propositions and theorems.

Let M be the Moore spectrum modulo an odd prime p given by the cof i bration

Let α：PqM→M be the Adams map and V(1)be its cof i bre given by the cof i bration

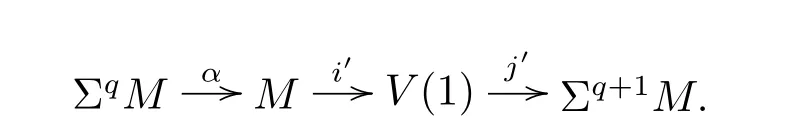
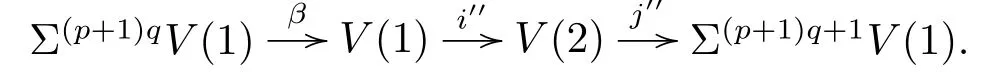
From[19],we know that the third periodicity family γsis represented by the third Greek letter family element

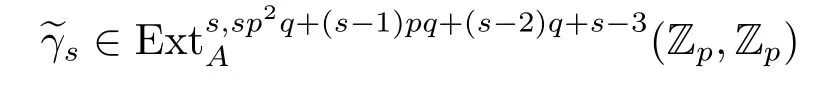
in the ASS,which is represented by the element

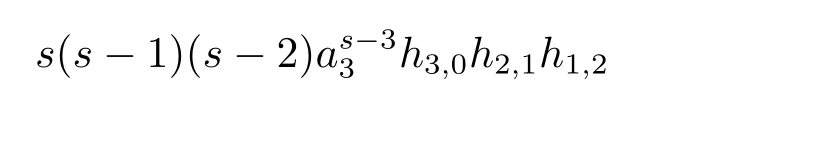
in the May spectral sequence(MSS).

Let L be the cof i bre of α1=jαiS→S given by the cof i bration

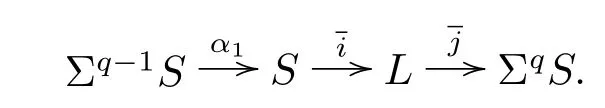
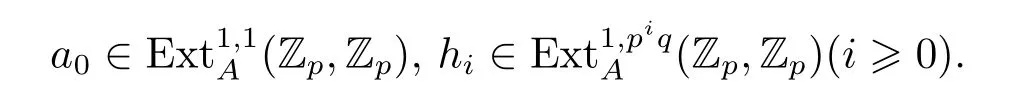
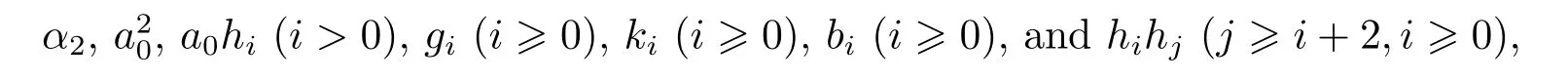
In the following,recall the Adams resolution of some spectra related to S from[4].Let

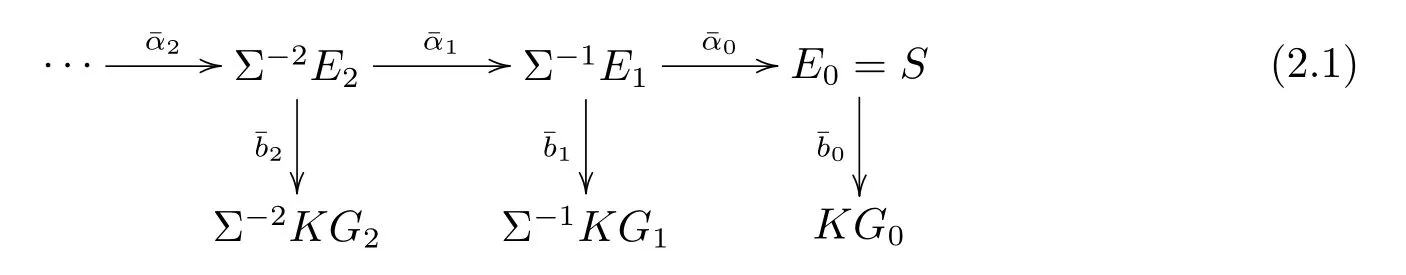
be the minimal Adams resolution of the sphere spectrum S which satis fi es

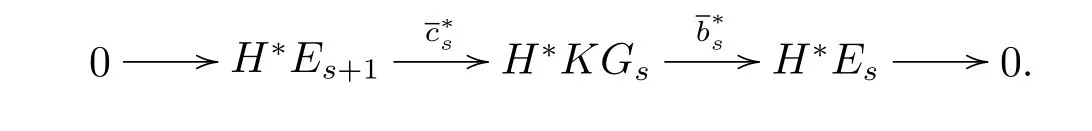
(B)KGsare the graded wedge sums of Eilenberg-Maclane spectrum KZpof type Zp. (C)πtKGsare the-terms of the ASS,

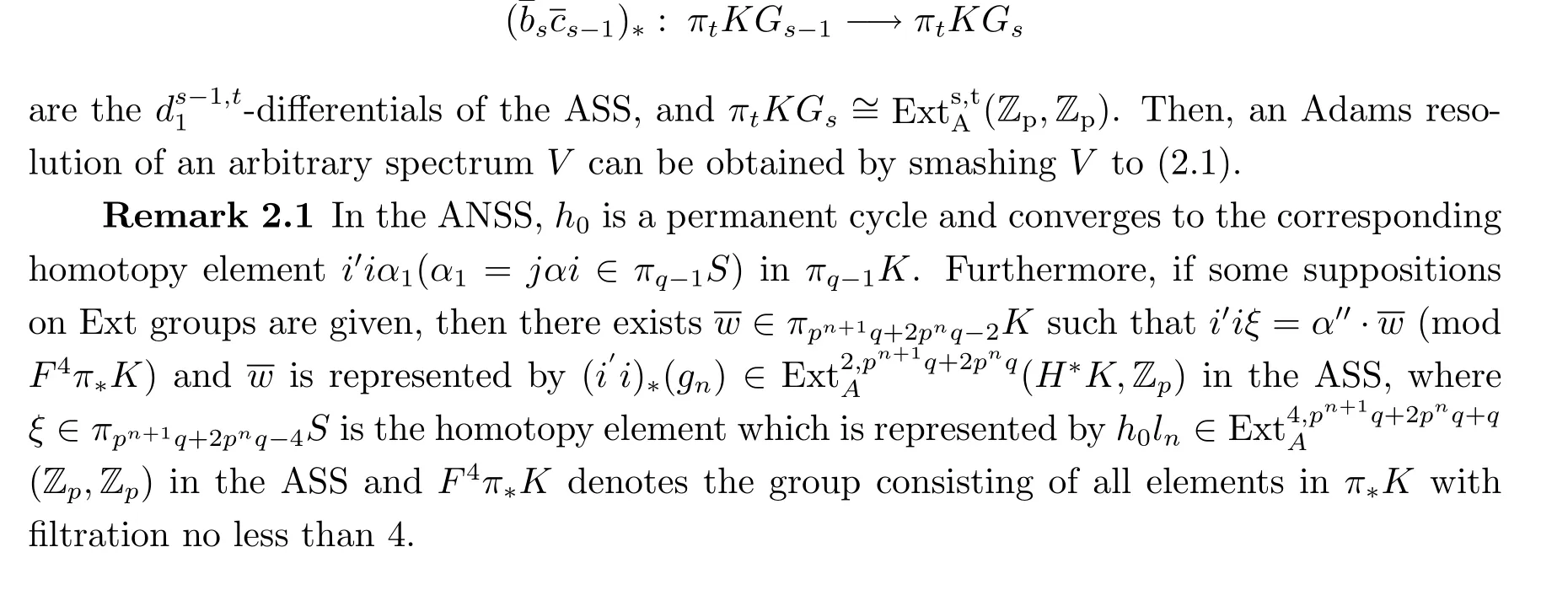
To detect π?S with the ASS,we must compute the E2-term of the ASS,Ext?A,?(Zp,Zp). The most successful method for computing it is the MSS.

From[13],there is a MSS{Ers,t,?,dr},which converges to ExtsA,t(Zp,Zp)with E1-term

where E()denotes the exterior algebra,P()denotes the polynomial algebra,and

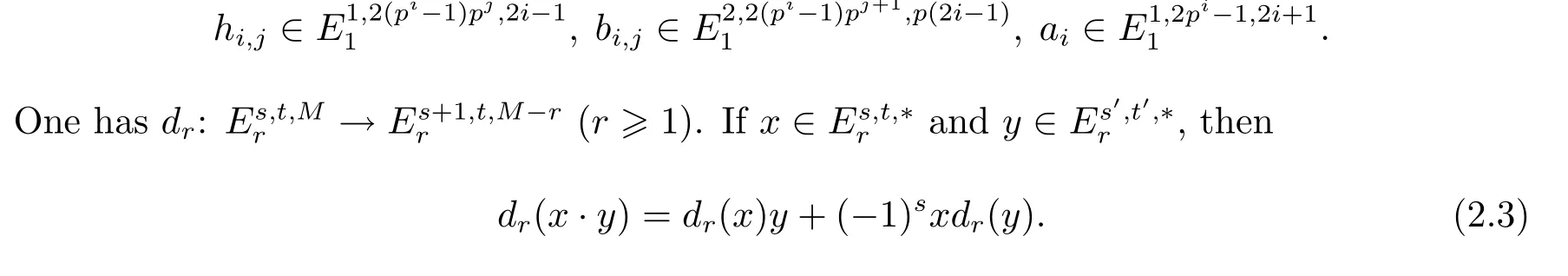
Furthermore,the May E1-term is graded commutative in the sense that

The fi rst May di ff erential d1is given by

For each element x∈E1s,t,?,if we denote dim x=s,deg x=t,we have

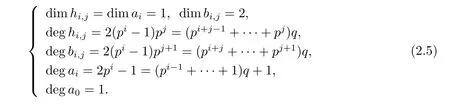
Remark 2.2 Any positive integer t can be expressed uniquely as t=···+c1p+c0)+e,where 0≤ci＜p(0≤i＜n),0＜cn＜p,0≤e＜q. Then,it is easy to get the following result from[16].

Proposition 2.3 In the MSS,we have=0 for some j(0≤j≤n),s＜cj,where s is also a positive integer with 0＜s＜p.

3 Some Adams E2-Terms

In this section,we mainly give some important results about Adams E2-terms.At the end,the proof of Theorem 1.1 will be given.

Proposition 3.1 Let 3≤s＜p-1,n＞3,p≥7,then

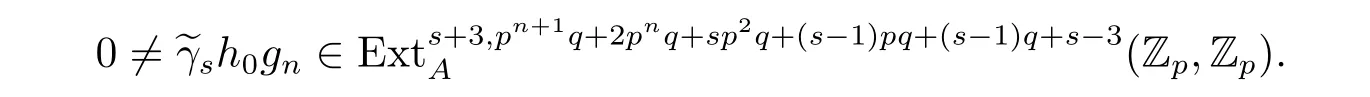
Proof Consider the structure ofin the MSS,where t=(s-1)pq+(s-1)q+s-3.Due to 3≤s＜p-1,then 5≤s+2＜p+1.

Case 1 5≤s+2＜p.Let h=x1x2···xmbe the generator of,where xiis one of ak,hi,jor bu,z,0≤k≤n+2,0＜i+j≤n+2,0＜u+z≤n+1,i＞0,j≥0,u＞0, z≥0.

Assume that degxi=+ei,where ci,j=0 or 1,ei=1 if xi=akor ei=0,then

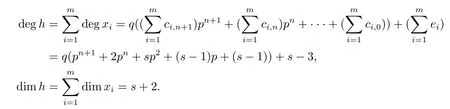
where t′=sp2q+(s-1)pq+(s-1)q+s-3.

We list all the possibilities of h′iin the following table(i=1,2,···,8),thus h doesn’t exist in this case.

Table 1：the possibilities of

Table 1：the possibilities of

The possibilityAnalysisThe existence of h′ih′1h′2h′3h′4 s-3＜m-3P i=1 ci,2=sNonexistent s-4＜m-3P i=1 ci,2=sNonexistent s-3＜h′4=as-33h22,0h1,0=0Nonexistent m-3P i=1 ci,2=sNonexistent h′5 s-1＜m-2P i=1 ci,2=sNonexistent h′6 s-1＜m-2P i=1 ci,2=sNonexistent h′7 s-2＜m-2P i=1 ci,2=sNonexistent h′8 s-2＜ci,2=sNonexistent m-3P i=1

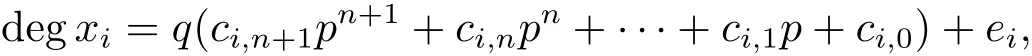
where ci,j=0 or 1,ei=1 if xi=akior ei=0,then

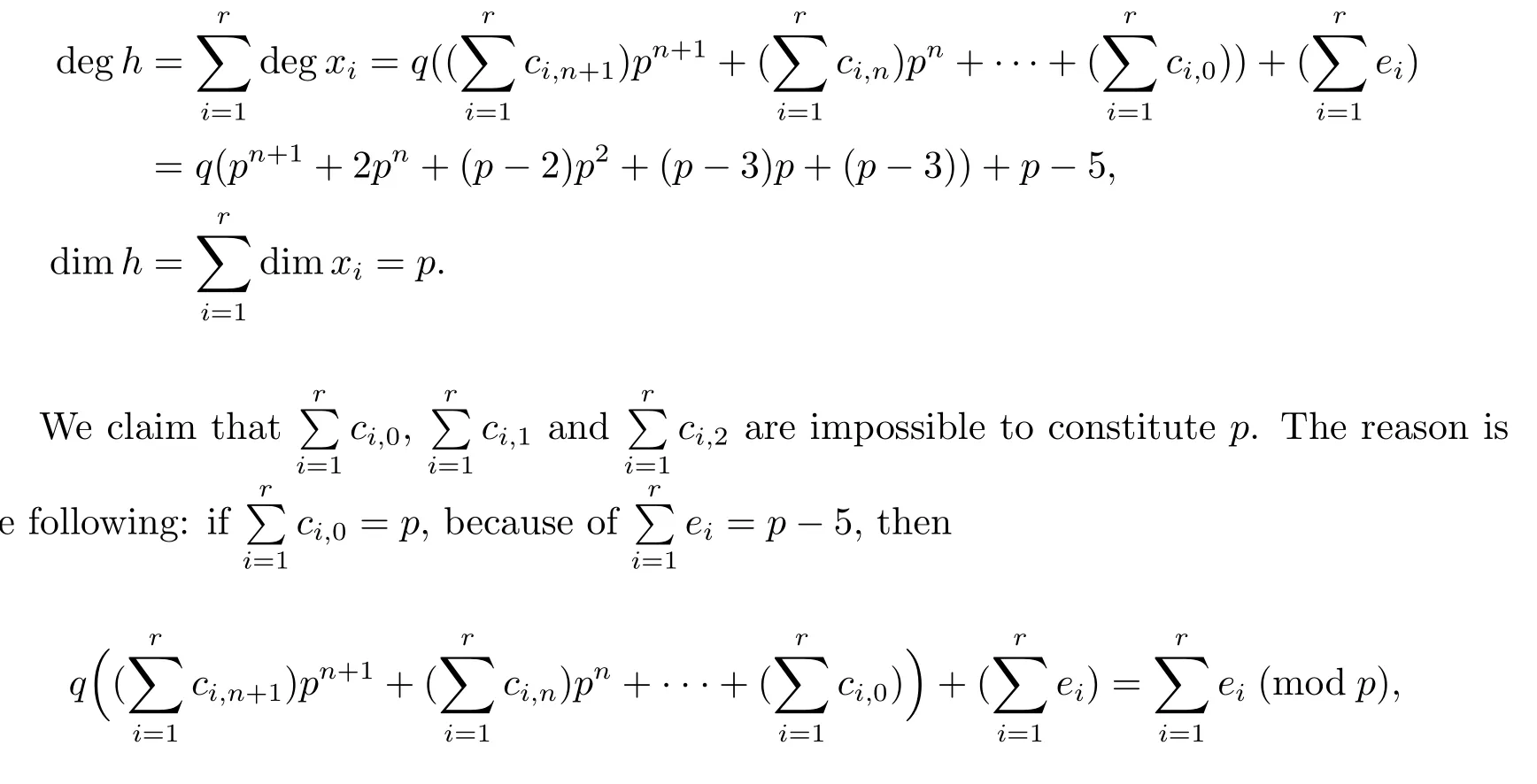
this contradicts to q(pn+1+2pn+(p-2)p2+(p-3)p+(p-3))+p-5=(p-3)q+p-5(modp). For the same reasonimpossible to constitute p.

From dimxi=1 or 2 and=p,we can see that r≤p.By Remark 2.2 andr≤p,ci,j=0 or 1,ei=0 or 1,we have

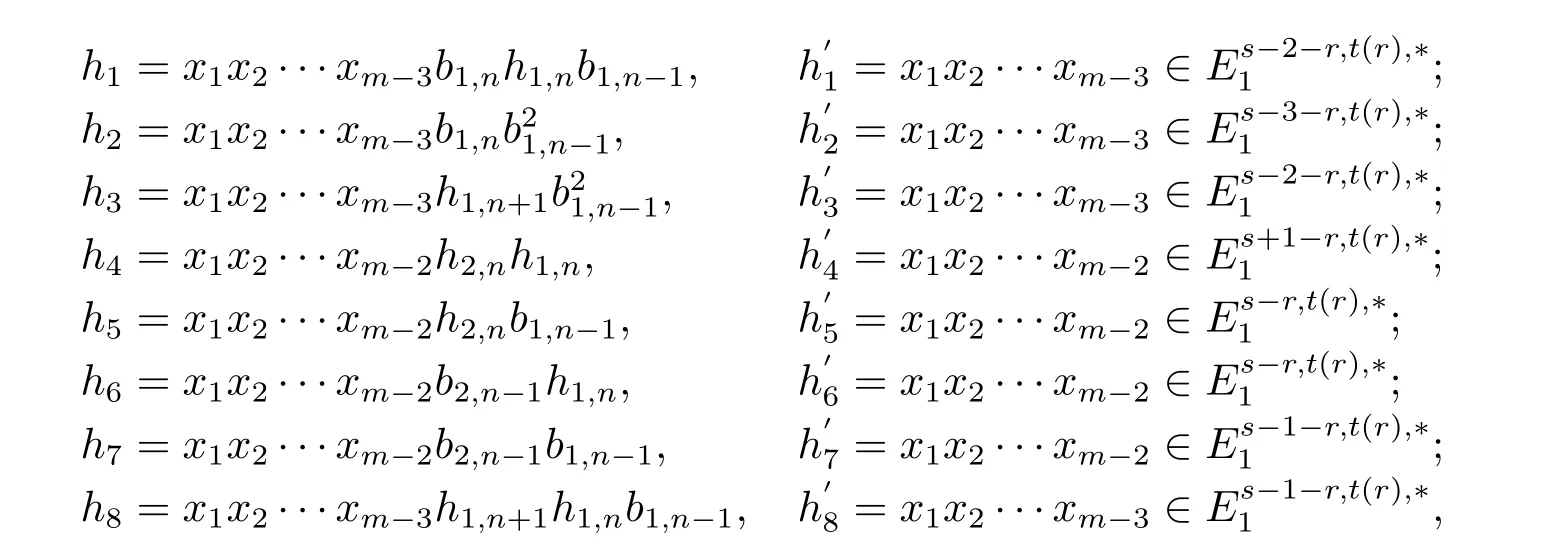
where t(r)=sp2q+(s-1)pq+(s-1)q+s-2-r.

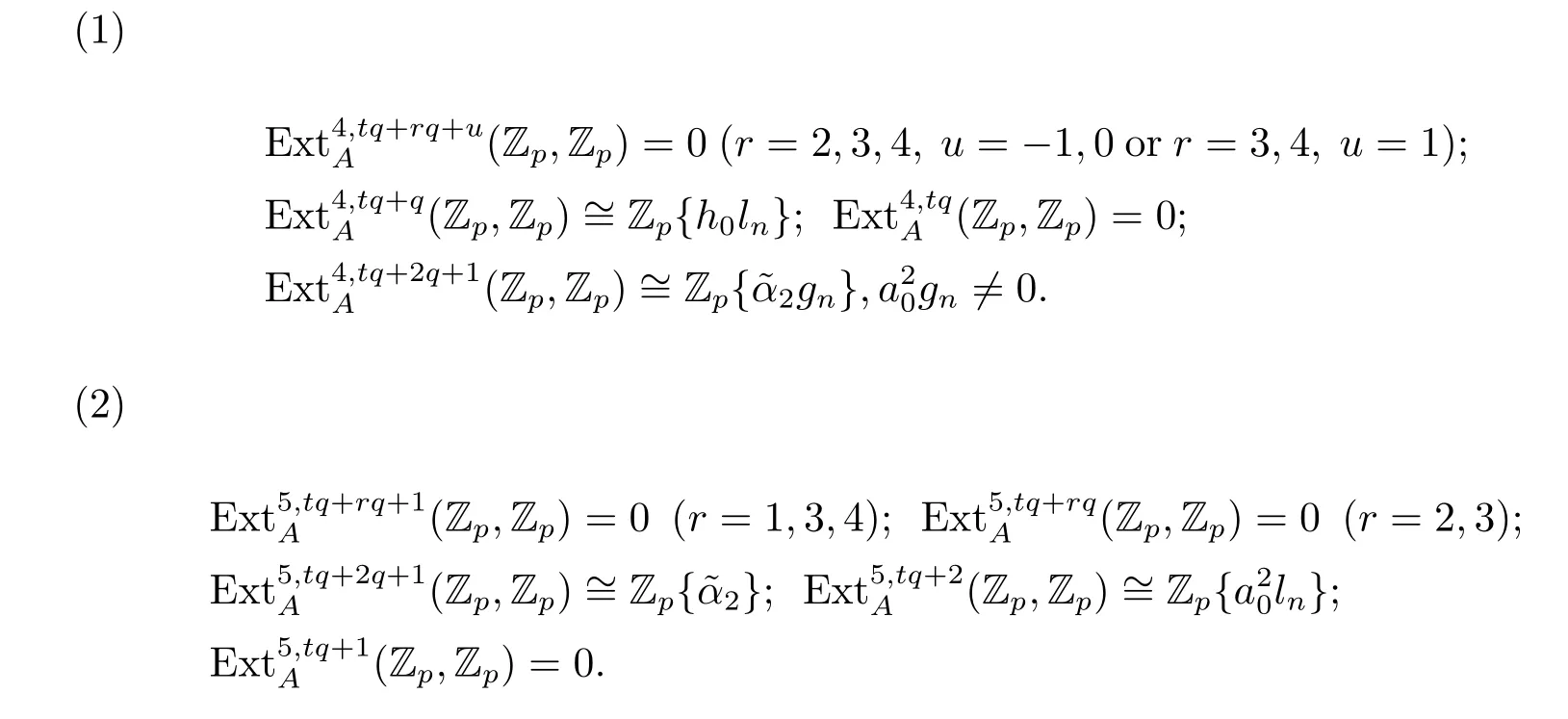
Proof(1)Consider the second degrees(mod pn+1q)of the generators in the E1-terms of the MSS,where 0≤j≤n+1,

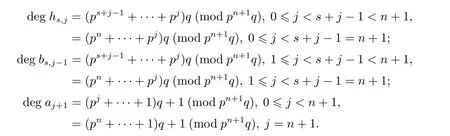
For the second degree k=tq+rq+u(0≤r≤4,-1≤u≤2)=2pnq+rq+u(mod pn+1q), and excluding the factor which has second degree≥tq+pq,we can get that the possibility of the factor of the generators in

b1,n,b1,n-1and b2,n-1.Thus from the degree we know that

Since a0,b1,n-1,h1,nand h1,n+1are all permanent cycles in the MSS and converge to a0,bn-1,hnand hn+1,respectively,it is easy to get that a0b1,n-1h1,nh1,n+1is a permanent cycle in the MSS and converges to a0bn-1hnhn+1which equals 0∈(Zp,Zp)byhnhn+1=0.Furthermore,we have d2p-1(b2,n-1)=b1,nh1,n-b1,n-1h1,n+1from[10],then d2p-1(a0b2,n-1b1,n-1)6=0 and so(Zp,Zp)=0.

Theorem 3.4 Let p≥7,n＞3,then

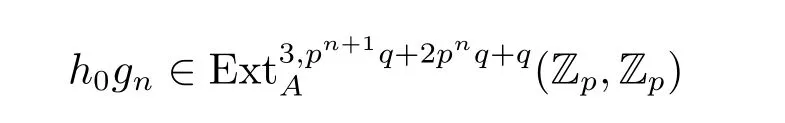
is a permanent cycle in the ASS,and converges to a nontrivial element in πpn+1q+2pnq+q-3S.

Proof From[20,Theorem 1.1],there is a nontrivial di ff erential d2(gn)=a0ln(n≥1) in the ASS,the elements gnand lnare called a pair of a0-related elements.The condition of Theorem A in[7]can be established by the Zp-bases of(s≤3)in[10] and Proposition 3.3 in the above.Furthermore,we have κ·(α1)L=(1E4∧p)f with f∈L,E4](see[7],9.2.34),then(1E4∧i)κ·(α1)L=0.Thus

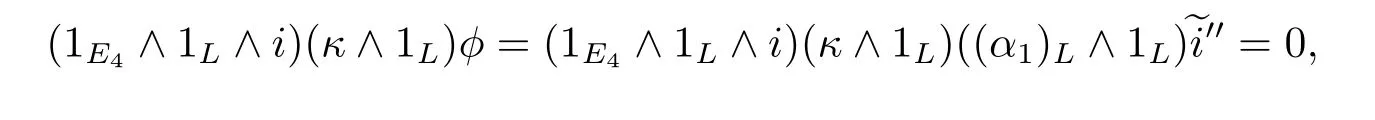
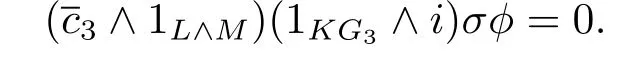
So we can get that(1L∧i)?φ?(gn)(H?L∧M,Zp)is a permanent cycle in the ASS.Then Theorem 3.4 will be concluded by Theorem C in[7],here φ∈S,L], κ∈πtq+1E4.

The Proof of Theorem 1.1 From Theorem 3.4,h0gn∈is a permanent cycle in the ASS and converges to a nontrivial elementS for n＞3.

Consider the following composition of mappings

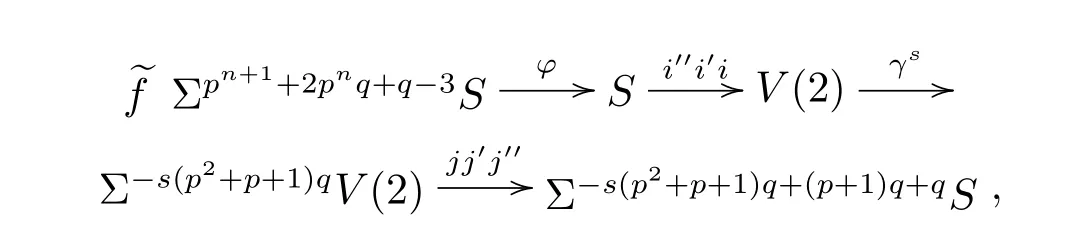
because φ is represented by h0gnin the ASS,then the above?f is represented by

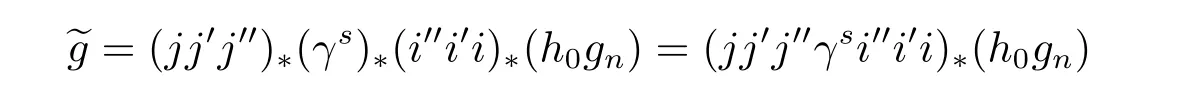
in the ASS.Furthermore,we know thatπ?S is represented byin the ASS.By using the Yoneda products,we know that the composition

is a multiplication(up to nonzero scalar)by

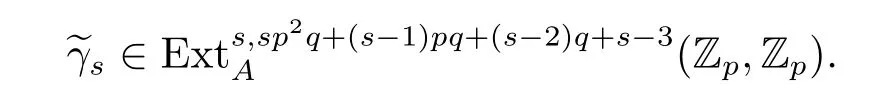
Hence,the composite map?f is represented(up to nonzero scalar)by

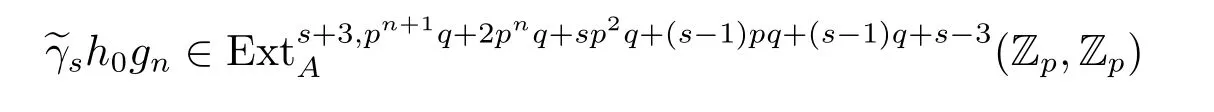
in the ASS.

From Proposition 3.1,we see that?γsh0gn6=0.Moreover,from Proposition 3.2,it follows that?γsh0gncan not be hit by any dif f erential in the ASS.Thus?γsh0gnsurvives nontrivially to a homotopy element in π?S.

[1]Adams J F.On the structure and application of Steenrod algebra[J].Comm.Math.Helv.,1958, 32(1)：180-214.

[2]Adams J F.Stable homotopy and generalized homotopy[M].Chicago：Univ.Chicago Press,1974.

[3]Aikawa T.3-dimensional cohomology of the mod p Steenrod algebra[J].Math.Scand.,1980,47：91-115.

[4]Cohen R,Goeress P.Secondary cohomology operations that detect homotopy class[J].Topology, 1984,23(2)：177-194.

[5]Cohen R.Odd primary inf i nite families in the stable homotopy theory[M].Providence RI：AMS, 1981.

[6]Lin J K.Third periodicity families in the stable homotopy of spheres[J].J.P.J.Geom.Topology, 2003,3(3)：179-219.

[7]Lin J K.Adams spectral sequence and stable homotopy groups of spheres(in Chinese)[M].Beijing：Science Press,2007,163-185.

[8]Liu X G.A new family represented by b1g0?γsin the stable homotopy of spheres[J].Sys.Sci.Math., 2006,26(2)：129-136.

[9]Lee C N.Detection of some elements in the stable homotopy groups of spheres[J].Math.Z.,1996, 222(2)：231-246.

[10]Liulevicius A.The factorizations of cyclic reduced powers by secondary cohomology operations[M]. Providence RI：AMS,1962.

[11]Mahowald M.A new inf i nite family in π?S[J].Topology,1977,16(3)：249-256.

[12]Miller H R,Ravenel D C,Wilson W S.Periodic phenomena in the Adams-Novikov spectral sequence[J].Ann.Math.,1977,106(3)：469-516.

[13]Ravenel D C.Complex cobordism and stable homotopy groups of spheres[M].New York：Academic Press,1986.

[14]Serre J P.Groupes d′homotopie et classes de groupes abeliens[J].Ann.Math.,1953,58(2)：258-294.

[15]Toda H.On spectra realizing exterior parts of the Steenrod algebra[J].Topology,1971,10(1)：53-65.

[16]Wang Y Y.A new familiy of f i ltration s+5 in the stable homotopy groups of spheres[J].Acta. Math.Sci.,2008,28(2)：321-332.

[17]Wang Y Y,Wang J L.A new family of elements in the stable homotopy groups of spheres[J].J. Math.,2015,35(2)：294-306.

[18]Wang Y Y,Wang J B.The nontrivility of ζn-related elements in the stable homotopy groups of sphere[J].Math.Scand.,2015,117：304-319.

[19]Wang X J,Zheng Q B.The convergencein Adams spectral sequence[J].Sci.China Math.,1998,41(6)：622-628.

[20]Zhao H,Wang X J.Two nontrivial di ff erentials in the Adams spectral sequence[J].Chinese Ann. Math.,2008,29A(1)：557-566.

[21]Zhong L N,Wang Y Y.Detection of a nontrivial product in the stable homotopy groups of spheres[J]. Alge.Geom.Top.,2013,13：3009-3029.

球面穩(wěn)定同倫群中第三周期γ類非平凡新元素

王玉玉1,王健波2

(1.天津師范大學數(shù)學科學學院,天津300387)
(2.天津大學理學院數(shù)學系,天津300072)

本文研究了球面穩(wěn)定同倫群的問題.以Adams譜序列中的第二非平凡微分為幾何輸入,給出了球面穩(wěn)定同倫群中h0gn(n＞3)的收斂性.同時,由Yoneda乘積的知識,發(fā)掘了球面穩(wěn)定同倫群中的一個非平凡新元素.非平凡元素的范圍將被我們的結果進一步擴大.

球面穩(wěn)定同倫群;Toda-Smith譜;Adams譜序列;May譜序列;Adams微分

O189.23

A

0255-7797(2017)05-0898-13

?Received date：2016-05-14Accepted date：2016-07-22

Supported by NSFC(11301386);NSFC(11001195)and Beiyang Elite Scholar Program of Tianjin University(0903061016);The Project Sponsored by the Scientif i c Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry.

Biography：Wang Yuyu(1979-),female,born at Handan,Hebei,professor,major in stable homotopy theory.

2010 MR Subject Classif i cation：55Q45