ON A SINGULAR ELLIPTIC SYSTEM INVOLVING THE CAFFARELLI-KOHN-NIRENBERG INEQUALITY

PENG Yan-fang

(Department of Mathematics and Science,Guizhou Normal University,Guiyang 550001,China)

ON A SINGULAR ELLIPTIC SYSTEM INVOLVING THE CAFFARELLI-KOHN-NIRENBERG INEQUALITY

PENG Yan-fang

(Department of Mathematics and Science,Guizhou Normal University,Guiyang 550001,China)

In this paper,we consider a singular elliptic system which involves critical exponent and the well-known Caffarelli-Kohn-Nirenberg inequality.By virtue of variational methods,we establish the existence of positive solution and sign-changing solution to the system,which partially extend the results in[19].

elliptic system;positive solution;sign-changing solution;singularity;Caffarelli-Kohn-Nirenberg inequality

1 Introduction

In this paper,we consider the following elliptic problem with singular coefficient

where Ω is a smooth bounded domain in RN(N≥ 3),0∈Ω,η ≥0,ai∈R,i=1,2,3,0≤For problem(1.1),we are interested in the existence and non-existence of a nontrivial solution(u,v),that is to say thatu0 andv0.Moreover,we call a solution(u,v)semi-trivial if(u,v)is type of(u,0)or(0,v).

Problem(1.1)can be seen as a counterpart of the following elliptic equation

In particular,whena=b=d=μ=0,problem(1.2)reduces to the Brezis-Nirenberg problem

In the well-known literature[5],Brezis and Nirenberg proved the existence of positive solutions to(1.3),when 0＜λ＜λ1(Ω),N≥ 4 andλ?＜λ＜λ1(Ω),N=3,whereλ1(Ω)is the fi rst eigenvalue of-Δ on Ω with Dirichlet boundary condition andλ?∈(0,λ1(Ω)).Moreover,in[11,13,28,29],sign-changing solutions to(1.3)were obtained.For(1.2),whena=b=d=0,μ/=0,i.e.,

For(1.4),Enrico Jannelli in[20]studied the role of space dimension on the existence of solutions,on one hand,the existence of positive solutions was obtained when;on the other hand,the non-existence of positive solutions was also proved in the case

Meanwhile,in[10,25],sign-changing solutions were proved to exist when.While for the nonexistence result,it was proved in[14]that(1.4)has no radial sign-changing solutions forλ∈(0,λ(N))when 3≤N≤6,Ω =B1(0),whereλ(N)＞0 depending onN.

For(1.2),it is clear that singularity occurs,the singularity of potentialis critical both from the mathematical and the physical point of view.As it does not belong to the Kato’s class,it cannot be regarded as a lower order perturbation of the laplacian but strongly in fl uences the properties of the associated elliptic operator.To be mentioned,singular potentials arise in many fi elds,such as quantum mechanics,nuclear physics,molecular physics,and quantum cosmology,we refer to[18]for further discussion and motivation.

Mathematically,(1.2)is related to the following well-known Caffarelli-Kohn-Nirenberg inequality(see[9])

Based on these results,a nature problem is：can we obtain the existence of positive solution and sign-changing solution for system(1.1)?In this paper,we will investigate the above problems and we obtain an affirmative answer.

To state our main results,we need to introduce some notations.

Setb=a+1 in(1.5),we have the following weighted Hardy inequality(see[7,12])

Hence norm(1.6)is well defined and equivalent to the usual norm

DenoteW：=H×Hto be the completion ofwith respect to the norm ‖(u,v)‖2：=‖u‖2+‖v‖2.

De fi ne the energy functional corresponding to problem(1.1)

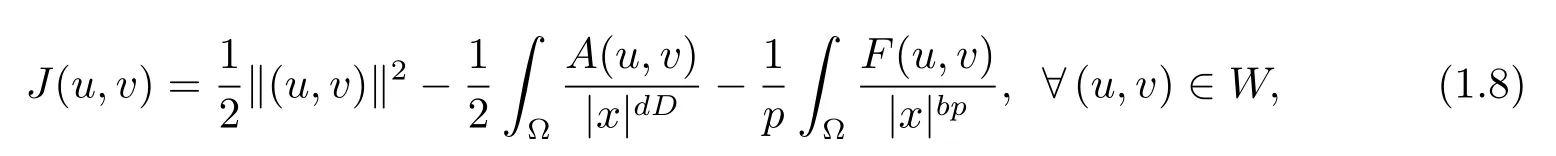
whereA(u,v) ：=a1u2+2a2uv+a3v2,F(u,v)：=|u|p+|v|p+η|u|α|v|β.ThenJ∈C1(W,R).The duality product betweenWand its dual spaceW-1is defined as

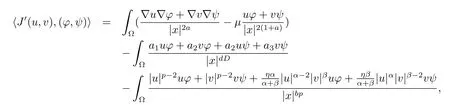
whereu,v,φ,ψ∈H.A pair of functions(u,v)∈Wis said to be a solution of problem(1.1)if

andλ1(μ)the fi rst eigenvalue of problem

By Sobolev inequality and Young inequality,the following best constants are well defined

Throughout this paper,we always assume that the following conditions：

(H2)ai≥ 0,i=1,2,3,,where Λ1and Λ2are the eigenvalues of the matrix

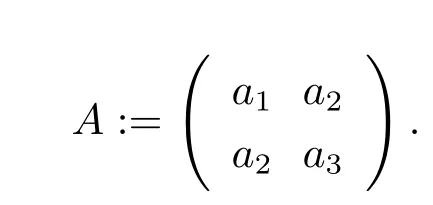
Our main results are as follows：

Theorem 1.1SupposeN≥4+4a-dDand(H1),(H2).,then(1.1)has a positive solution inWwhen,then(1.1)has a positive solution inWwhen

Theorem 1.2Suppose(H1),(H2),η=0,N≥max{ 6(1+a)-2dD,4+2a},,then(1.1)has a pair of sign-changing solutions.

Remark 1.3Theorem 1.2 says that whena=b=d=0,(1.1)has a pair of signchanging solutions.This result generalizes the results of Theorem 1.3(i)in[19].

To verify Theorem 1.1,we mainly employ the framework in[5,20].However,the singularity of the solutions and the non-uniform ellipticity of the operator-div(|x|-2a?·)bring us more difficulties,so we need to fi nd new arguments.On one hand,to obtain positivesolutions,a new maximum principle should be established;on the other hand,we need to estimate the asymptotic behavior(near the origin)of(1.2).Moreover,whether or notλ1(μ)can be attained is not clear and we also need to estimateλ1(μ)and

To obtain Theorem 1.2,our methods are inspired by the work of[19].However,comparing with[19],since the generality of(1.1),more complex calculation will be needed.

This paper is organized as follows.In Section 2,we will give some important preliminaries.A positive solution will be obtained in Section 3 by using the mountain pass lemma.In the last section,we will discuss the existence of sign-changing solutions.In this paper,for simplicity,we denoteC(may be di ff erent in di ff erent places)positive constants,Br(x)：={y∈RN：|y-x|＜r}and we omitdxin the integral.

2 Preliminaries

In this section,we shall give some preliminaries and a non-existence result.

Lemma 2.1Suppose.Then

(i)S(μ)is independent of Ω.

(ii)When Ω =RN,S(μ)can be achieved by the functions

for allε＞0.The functionsUε(x)solve the equation

ProofThe result was proved in[7,12].

Lemma 2.2Suppose(H1)and(H2),then

(i)Sη,α,β(μ)=f(τmin)S(μ).

(ii)Sη,α,β(μ)has the minimizers(Uε(x),τminUε(x)),?ε＞0,where1 andτminsatisfies

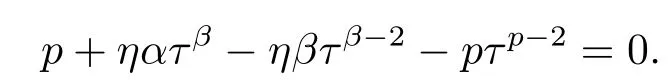
ProofThe proof is similar to Theorem 1.1 in[19].Here we omit it.

Lemma 2.3Letτ＞2-N.Suppose thatu∈C2(Ω{0}),u≥ 0,u/≡0 satis fi es-div(|x|τ?u)≥ 0,thenu＞0 in Ω{0}.

ProofThe proof is similar to[6]or[7].Here we omit it.

Lemma 2.4Suppose that(H1),(H2)and(u1(x),v1(x))∈Wis a positive solution of(1.1),then

(i)if 0≤μ＜(-a)2,then for anyBρ(0)?Ω,there exist 0＜C1＜C2＜ ∞such that

(ii)0≤λ1(μ)＜(μ).

ProofThe proof is similar to[6]and[20].Here we omit it.

To complete this section,we give a nonexistence result of solutions for(1.1).

Lemma 2.5If Ω is star-shaped with respect to the origin and Λ2≤0,then(1.1)has no solution inW.

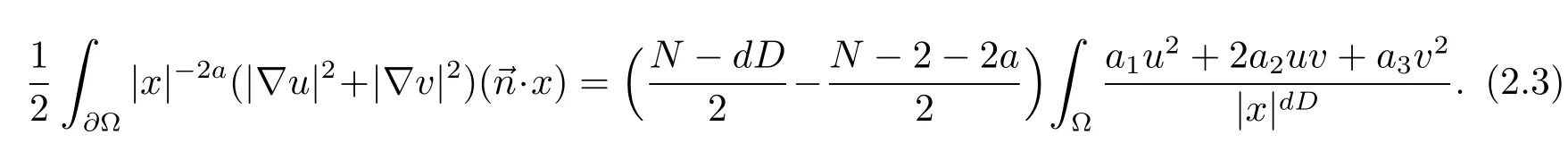
ProofThe proof is based on a Pohozaev’s type identity which can be verified by the similar method as[7].by our assumptions,hence(2.3)is impossible in the case Λ2≤0 since the left hand side of(2.3)is positive.So we complete our proof.

From Lemma 2.5,to obtain positive solution of(1.1),we impose the condition Λ1,Λ2＞0.

3 Positive Solution to Problem(1.1)

In this section,we will prove Theorem 1.1.SinceJ∈C2(W,R),we see that critical points of functionalJcorrespond to the weak solution of(1.1).

Lemma 3.1Suppose(H1)and(H2)hold.ThenJ(u,v)satis fi es the(PS)ccondition for

ProofThe proof is standard(see[5]for example)and we omit it.

Set

Set

Proof of Theorem 1.1Under assumption(H2),we have

Meanwhile,for anyv∈D1,2(RN,|x|-2a)andφ∈D,we see

Takingv=Uε,we obtain

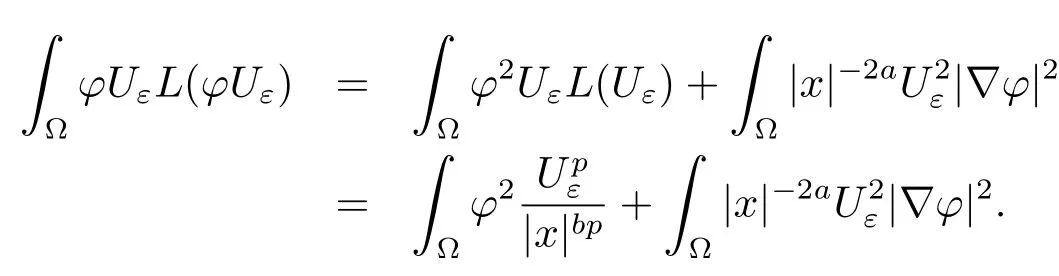
So fort＞0,

From(3.1)-(3.5),we see that forεsufficiently small,there exists boundedtεsuch thatHenceand

On the other hand,asε→0,

thus

Hence,considering 2a＜dD,we see that for a fi xedφ∈D,and any,we can chooseεsufficiently small such that

Therefore,forεsmall enough,

which is exactly(3.7).

By Lemma 2.4 and density arguments,for any,there existsφ∈D,such that(3.10)holds forεsufficiently small.Hence we also obtain(3.7).

4 Sign-Changing Solutions to Problem(1.1)

Let(u0,v0)be the positive solution of(1.1)obtained in Theorem 1.1 and setc0：=J(u0,v0).From[26],we can infer thatc0can be characterized by,where

Letg(u,v)be the functional defined inWby

Setu+=max{u,0},u-=max{-u,0}.De fi ne

thenσ ∈Σ fork＞0 large enough.

Lemma 4.1There exists a sequencesuch that

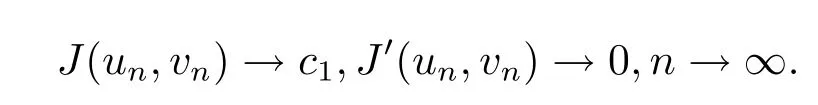
Furthermore,

ProofThe proof is similar to that of[25].Here we omit it.

Lemma 4.2Suppose that(H1)-(H3)hold.Ifc1＜c0+c?and{ (un,vn)}?satis fi es

then{ (un,vn)}is relatively compact inW.

ProofAccording to Lemma 2.1 and following the same lines as in[25],we can obtain the result.Here we omit it.

Lemma 4.3Suppose that(H1),(H2),η=0 andβ?＞max{ 2(1+a)-dD,1},thenc1＜c0+c?.

ProofBy the proof of Theorem 1.1,we infer thatτmin=0 andS0,α,β=S(μ).In this case,.By Lemma 4.1,it suffices to show that

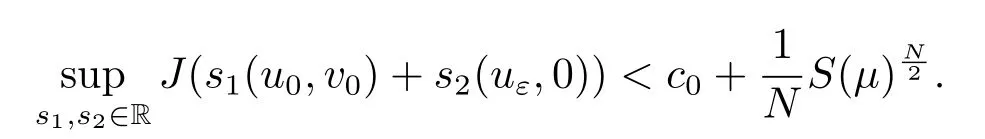
Since

we may assume that there exist constants 0＜C1＜C2such thatC1≤|si|≤C2,i=1,2.Note that the following elementary inequality holds：?q∈[1,+∞),there exists a constantC=C(q)＞0 such that

Since(u0,v0)is a positive solution of(1.1),we have that〈J′(u0,v0),(φ,ψ)=0,i.e.,

In particular,〈J′(u0,v0),(uε,0)〉=0.Consequently,

From Lemma 2.4,it follows that

Similarly,

Arguing as the proof of Theorem 1.1 and by(3.1)-(3.4),(4.1)-(4.2),we have

where we use the fact thatβ?＞max{ 2(1+a)-dD,1}.

Proof of Theorem 1.2By Lemma4.1-Lemma4.3,there exists a sequence{ (un,vn)}?such that

Passing to a subsequence if necessary,(un,vn)→(u,v)inWasn→∞.Therefore(u,v)is a critical point ofJand solves(1.1).Since(un,vn)∈,we infer that(u,v)∈.Moreover,we have00.It follows from the H¨older and Young inequality that there exists a constantδ＞0 such that

Therefore(u,v)is a sign-changing solution of(1.1)and(-u,-v)is also a solution.So far,the proof of Theorem 1.2 is completed.

[1]Abdellaoui B,Colorado E,Peral I.Existence and nonexistence results for a class of linear and semilinear parabolic equations related to some Caffarelli-Kohn-Nirenberg inequalities[J].J.Eur.Math.Soc.,2004,6：119-148.

[2]Abdellaoui B,Colorado E,Peral I.Some improved Caffarelli-Kohn-Nirenberg inequalities[J].Calc.Var.Part.Di ff.Equ.,2005,23：327-345.

[3]Abdellaoui B,Felli V,Peral I.Existence and multiplicity for perturbations of an equation involving Hardy inequality and critical Sobolev exponent in the whole RN[J].Adv.Di ff.Equ.,2004,9：481-508.

[4]Abdellaoui B,Peral I.On quasilinear elliptic equations related to some Caffarelli-Kohn-Nirenberg inequalities[J].Comm.Pure Appl.Anal.,2003,2：539-566.

[5]Brezis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents[J].Comm.Pure Appl.Math.,1983,36：437-477.

[6]Chen J.Multiple positive solutions for a class of nonlinear elliptic equations[J].J.Math.Anal.Appl.,2004,295：341-354.

[7]Chou K,Chu C.On the best constant for a weighted Sobolev-Hardy inequality[J].J.London Math.Soc.,1993,48：137-151.

[8]Cao D,Han P.Solutions to critical elliptic equations with multi-singular inverse square potentials[J].J.Di ff.Equ.,2006,224：332-372.

[9]Caffarelli L,Kohn R,Nirenberg L.First order interpolation inequality with weights[J].Compositio Math.,1984,53：259-275.

[10]Cao D,Peng S.A note on the sign-changing solutions to elliptic problems with critical Sobolev exponent and Hardy terms[J].J.Di ff.Equ.,2003,193：424-434.

[11]Cerami G,Solimini S,Struwe M.Some existence results for superlinear elliptic boundary value problems involving critical exponents[J].J.Funct.Anal.,1986,69：289-306.

[12]Catrina F,Wang Z.On the Caffarelli-Kohn-Nirenberg inequalities：sharp constants,existence(and nonexistence),and symmetry of extermal functions[J].Comm.Pure Appl.Math.,2001,54：229-258.

[13]Roselli P,Willem M.Least energy nodal solutions of the Brezia-Nirenberg problem in dimensionN=5[J].Comm.Contemp.Math.,2009,1：59-69.

[14]Deng Y,Wang J.Nonexistence of radial node solutions for elliptic problems with critical exponents[J].Nonl.Anal.,2009,71：172-178.

[15]Ferrero A,Gazzola F.Existence of solutions for singular critical growth semilinear elliptic equations[J].J.Di ff.Equ.,2001,177：494-522.

[16]Felli V,Schneider M.Perturbation results of critical elliptic equations of Caffarelli-Kohn-Nirenberg type[J].J.Di ff.Equ.,2003,191：407-426.

[17]Felli V,Schneider M.Compactness and existence results for degenerate critical elliptic equations[J].Comm.Contemp.Math.,2005,7：37-73.

[18]Frank W,Land D,Spector R.Singular potentials[J].Rev.Modern Phys.,1971,43：36-98.

[19]Huang Y,Kang D.On the singular elliptic systems involving multiple critical Sobolev exponents[J].Nonl.Anal.,2011,74：400-412.

[20]Jannelli E.The role played by space dimension in elliptic critical problems[J].J.Di ff.Equ.,1999,156：407-426.

[21]Ni W.Recent progress in semilinear elliptic equations[J].Math.Report Minnesota,1989,679：88-117.

[22]Peng Y.Existence and concenteration behavior of node solutions for a Kirchho ffequations in R3[J].J.Math.,2015,35(1)：75-84.

[23]Peng Y,Li B.Existence and nonexistence of sign-changing solutions for a singular elliptic problem[J].Acta Math.Sinica,Chinese Series,2014,57：281-294.

[24]Peng S,Peng Y.Least energy radial sign-changing solutions for a singular elliptic equation in lower dimensions[J].Comm.Cont.Math.,2014,16,1350048(16 pages).

[25]Tang Z.Sign-changing solutions of critical growth nonlinear elliptic systems[J].Nonl.Anal.,2006,64：2480-2491.

[26]Willem M.Minimax theorems[M].Boston：Birkh¨auser,1996.

[27]Wang Z,Willem M.Singular minimization problems[J].J.Di ff.Equ.,2000,161：307-320.

[28]Yarantello G.Nodal solutions of semilinear elliptic equations with critical exponent[J].Di ff.Integral Equ.,1992,5：25-42.

[29]Zhang D.On multiple solutions of.Nonl.Anal.,1989,13：353-372.

一類與Caffarelli-Kohn-Nirenberg不等式有關(guān)的奇異橢圓型方程組

彭艷芳

(貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,貴州貴陽 550001)

本文研究了一類與Caffarelli-Kohn-Nirenberg不等式有關(guān)的帶臨界指數(shù)的奇異橢圓型方程組.利用變分方法,證明了方程組的正解及變號解的存在性.結(jié)果部分推廣了文獻(xiàn)[19]的結(jié)果.

橢圓型方程組;正解;變號解;奇異性;Caffarelli-Kohn-Nirenberg不等式

O175.23

on：35J60;35B33

A Article ID： 0255-7797(2017)04-0685-13

date：2015-08-29Accepted date：2016-02-18

Supported by National Natural Science Foundation of China(11501143);the Ph.D Launch Scienti fi c Research Projects of Guizhou Normal University(2014).

Biography：Peng Yanfang(1982-),female,born at Xinyu,Jiangxi,associate professor,major in partial di ff erential equations.