A Generalized Schwarz Lemma

ZHAO Lian-kun,LI Hong-yi

(LIIB.School of Mathematics and System Science,Beihang University,Beijing 100191,China)

A Generalized Schwarz Lemma

ZHAO Lian-kun,LI Hong-yi

(LIIB.School of Mathematics and System Science,Beihang University,Beijing 100191,China)

In this paper,we establish a boundary Schwarz Lemma for holomorphic mapping on the generalized complex ellipsoid in Cn.

several complex variables;Schwarz Lemma;generalized complex ellipsoid

§1.Introduction

Schwarz lemma is the most fundamental and significant result in complex analysis,having attracted wide attention and analysis over the past century.This noted lemma reveals that the range of homomorphic functions,which satisfy certain condition,will be compressed along with its domain of definition.As is well known,Riemann mapping theorem is no longer valid in several complex variables.Even two of the most simple domains unit ball Bnand polydisc Dnin several complex variables are not holomorphic equivalent.Therefore,it is essential to study the corresponding versions of Schwarz lemma in distinct domains in several complex variables.

1.1 Schwarz Lemma in One Complex Variable

In one complex variables,the following Schwarz Lemma is classical[1].

Theorem ALet is unit disk in complex plane C and f:D→D is a homomorphic function.If f(0)=0,then?ζ∈D,

The above equality holds if and only if f(z)=cz,where|c|=1.

The classical result was first introduced by H A Schwarz in 1869.According to this lemma, if a holomorphic function f of D into itself with f(0)=0,then the module of range can be controlled by the module of domain of definition.

Given a boundary point,there is a boundary Schwarz Lemma

Theorem BLet is a unit disk in complex plane C and let f:D→D be a holomorphic function.Iffis holomorphic at z=1 and f(0)=0,f(1)=1,then f′(1)≥1.Moreover,the inequality is sharp.

RemarkNotice that,if the condition of f(0)=0 in Theorem A is removed and apply Theorem B to

one can get

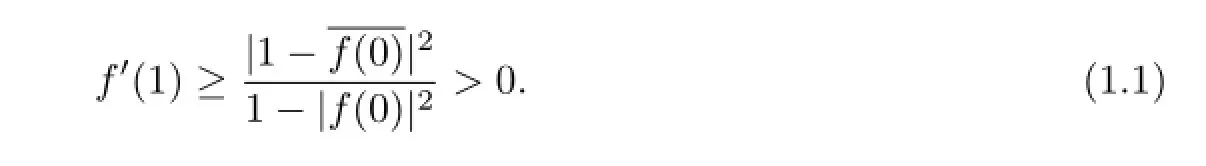
Before taking a closer look at Schwarz lemma,some notations and definitions are given.

1.2 Some Notations and Definitions

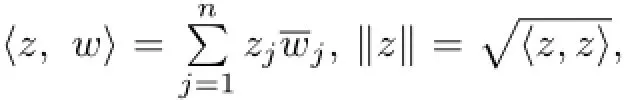
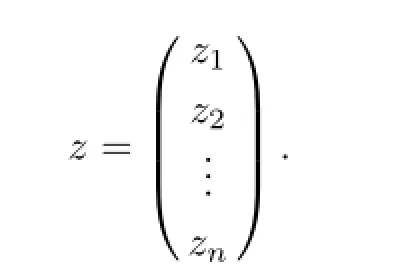
The derivative of f=(f1,f2,···,fn)Tat z0is the complex Jacobi matrix of f,which is defined as follows,

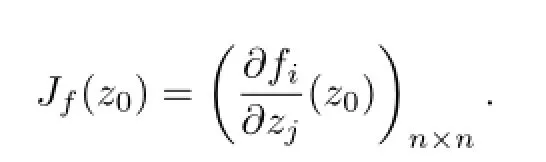
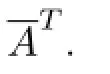
Definite 1Let ? be a domain in Cn.If for any(z1,···,zn)T∈? and θ1,···,θn∈R, one can get

then ? is called Reinhardt domain.

Definite 2Generalized complex ellipsoid in Cnis defined as follows,

where n≥2,p＞0.

Definite 3z0∈Bp,n,the tangent space Tz0(?Rp)to?Rpat z0is defined by

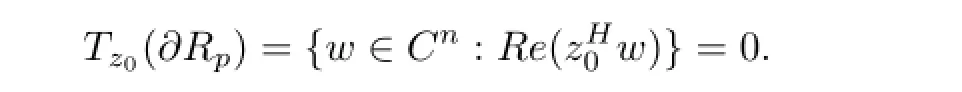
Notice that,generalized complex ellipsoid Bp,nis bounded and is a special kind of Reinhardt domain.

1.3 Relative Results

Theorem 1[2]Let ? denote bounded domains in Cn,f is a holomorphic function of ?, p∈? is a fixed point,then

(1)The module of all eigenvalues of Jf(p)less than 1;

(2)|det Jf(p)|≤1;

(3)If|det Jf(p)|=1,then f is a biholomorphism mapping of ?.

Theorem 2[3]Let ? be a bounded strongly pseudoconvex domain in Cn,p∈??,f:?→? is a holomorphic function,when z→p,f(z)=z+O(|z-p|4),then f(z)≡z.

Theorem 3[4]Let ? be a strictly convex domains in Cn(n＞1),p∈??,f:?→?is a holomorphic function,for a certain point z0∈?,f(z0)=z0and when z→p,f(z)= z+O(|z-p|2).then f(z)≡z.

For the past few years,plenty of research and development work is being done about Schwarz Lemma in many distinctive domains in Cn,which includes boundary Schwarz Lemma between unit ball Bnin Cn[5],between polydisk Dnin Cn[6],form polydisk Dnto unit ball Bn[7], strictly convex domains Cn[8],strongly pseudoconvex domain[9]and between a special kind of Reinhardt domain Bp1,p2={(z1,z2,···,zn)T∈Cn:|z1|p1+|z2|p2+···+|zn|p2＜1}, p1≥1,p2≥1[10].

§2.A Boundary Schwarz Lemma for Holomorphic Mapping on the Generalized Complex Ellipsoid in Cn

We establish a boundary Schwarz Lemma of generalized complex ellipsoid Bp,nin this paper and the main results are as follows.

Theorem 2.1Let Bp,nis a generalized complex ellipsoid in Cn,where n≥2,p＞0. f:Bp,n→Bp,nis a holomorphic mapping,z0∈S,where S=?Bp,nT?Bn,f is holomorphic at z0,f(z0)=z0,then the eigenvalues of Jf(z0)λ1,μ2,···,μnsatisfy the following statements

(1)z0is the eigenvector of Jf(z0)Hwith respect to λ.That is to say,Jf(z0)Hz0=λz0;

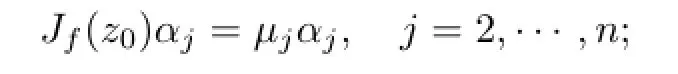
Proof

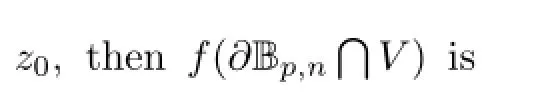
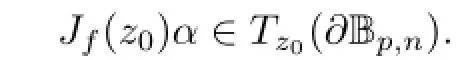
So,for any α∈Tz0(?Bp,n),

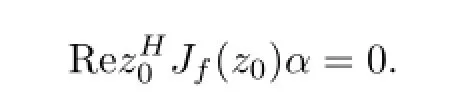
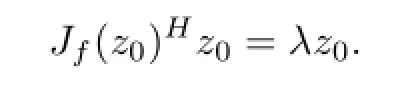
This shows that λ is a eigenvector of Jf(z0)H.λ is a real number,then λ is the eigenvalue of Jf(z0)

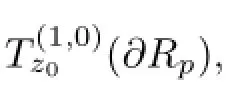
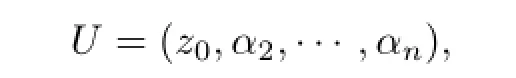
then U is a unitary matrix of order n.Because Jf(z0)Hz0=λz0,we get

where V is a complex matrix of order(n-1),B is an complex matrix of order(n-1)×1. Hence,

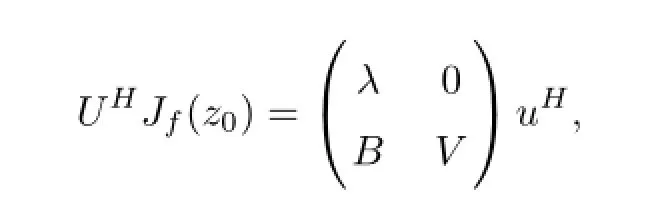
that is,

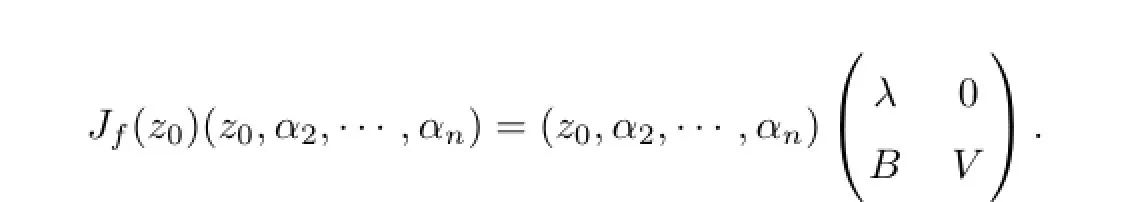
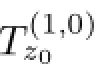
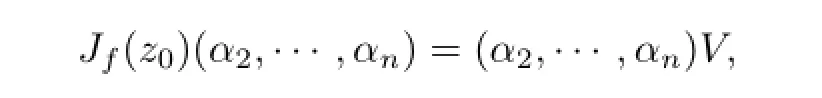
the roots of det(xIn?1-V)areμ2,···,μn.If λ/∈{μ2,···,μn},then λ,μ2,···,μnare all eigenvalues of Jfz0.

Suppose that λ=μi0is a zero point of order k of det(xIn?1-V)and Jf(z0)is a linear transformation on Cn,then characteristic polynomial of Jf(z0)is

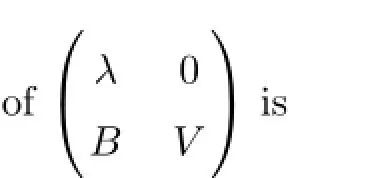
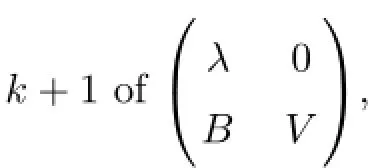
(3)According to hypothesis S=?Bp,nT?Bn,obviously(eiθ,0,···,0)T,···,(0,···,0,eiθ)T∈S,so S is not empty.

Without loss of generality,z0=(eiθ,0,···,0)T.z0=(0,···,0,eiθ,0,···,0)T,j-th element of which is eiθ,can be transformed to z0=(eiθ,0,···,0)Tby a simple permutation transformation ψ

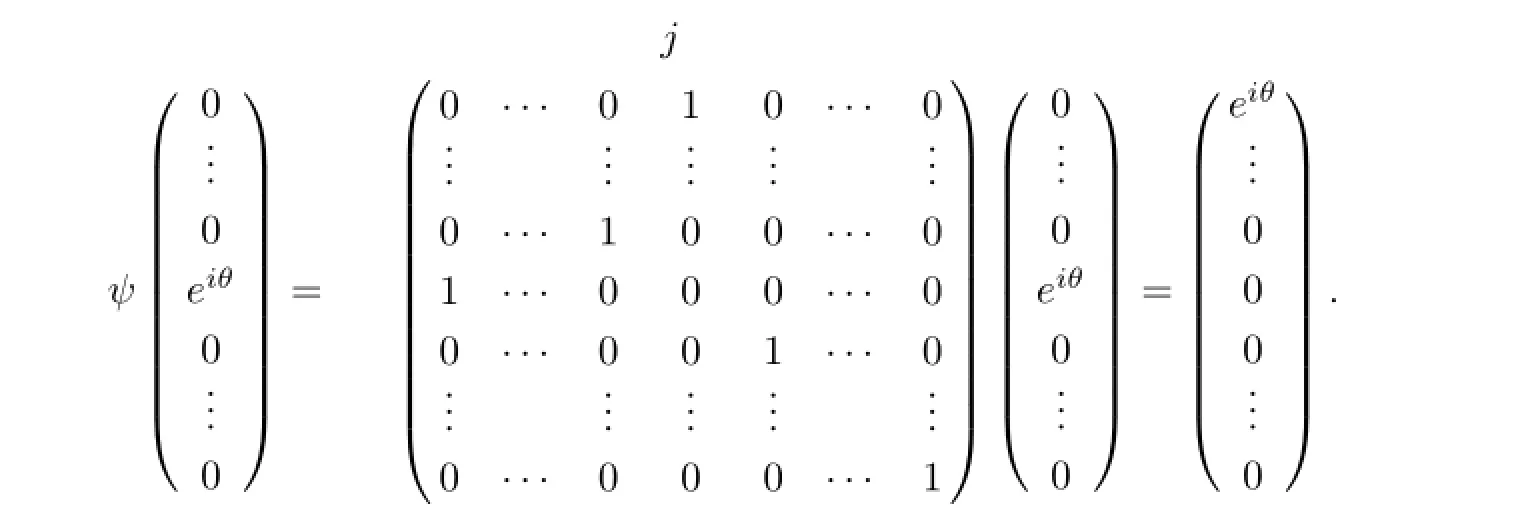
where a=f(0),if a=0,it follows that λ≥1.

[1]YIN Wei-ping.The Bergman kernel function of super-Cartan domain of the first type[J].Science in China, 1999,29A(7):607-615.

[1]GARNETT J B.Bounded Analytic Functions[M].New York:Springer,2007.

[2]WU Hong-xi.Normal families of holomorphic mappings[J].Acta Mathematica,1967,119(1):193-233.

[3]BURNS D M,KRANTZ S G.Rigidity of holomorphic mappings and a new Schwarz Lemma at the boundary[J].Journal of the American Mathematical Society,1994,7(3):661-676.

[4]HUANG Xiao-jun.A boundary rigidity problem for holomorphic mappings on some weakly pseudoconvex domains[J].Canadian Journal of Mathematics,1995,47(2):405-420.

[5]LIU Tai-shun,WANG Jian-fei,TANG Xiao-min.Schwarz Lemma at the boundary of the unit ball in C n and its applications[J].The Journal of Geometric Analysis,2015,25(3):1890-1914.

[6]TANG Xiao-min,LIU Tai-shun,LU Jin.Schwarz Lemma at the boundary of the unit polydisk in Cn[J]. Science China Mathematics,2015,58(8):1639-1652.

[7]LIU Yang,CHEN Zhi-hua,PAN Yi-fei.A boundary Schwarz Lemma for holomorphic mappings from the polydisc to the unit ball[J].2014,arXiv preprint arXiv:1411.0603.

[8]WANG Xie-ping.Schwarz Lemma at the boundary of strongly convex domains in Cn[J].Complex Analysis and Operator Theory,2015,11(2):1-14.

[9]LIU Tai-shun,TANG Xiao-min.Schwarz Lemma at the boundary of strongly pseudoconvex domain in Cn[J].Mathematische Annalen,2016,366(1-2):655-666.

[10]ZHANG Xiao-fei.Schwarz Lemma at the Boundary for Several Complex Variables and Its Applications[D]. Hefei:University of Science and Technology of China,2013.

tion:32H02,30C80,32A30

:A

1002–0462(2017)01–0001–06

date:2016-10-23

Supported by the National Natural Science Foundation of China(61379001)

Biographies:ZHAO Lian-kun(1991-),male,native of Tengzhou,Shandong,a master of mathematics of Beihang University,engages in complex analysis;LI Hong-yi(corresponding author)(1960-),female,native of Kaifeng,Henan,a professor of Beihang University,Ph.D.,engages in complex analysis and its application.

CLC number:O174.56