Existence and Uniqueness of Solutions to Singular Higher Order Two-point BVPs on Time Scales

TENG Nan,MA Fu-bo,YU Tong,MO Ran

(1.Department of Mathematics,Harbin University,Harbin 150086,China;2.Department of Civil Engineering,Harbin University,Harbin 150086,China)

Existence and Uniqueness of Solutions to Singular Higher Order Two-point BVPs on Time Scales

TENG Nan1,MA Fu-bo2,YU Tong2,MO Ran1

(1.Department of Mathematics,Harbin University,Harbin 150086,China;2.Department of Civil Engineering,Harbin University,Harbin 150086,China)

This paper investigates the existence and uniqueness of solutions for singular higher order boundary value problems on time scales by using mixed monotone method. The theorems obtained are very general.For the different time scale,the problem may be the corresponding continuous or discrete boundary value problem.

time scale;boundary value problem;mixed monotone operator;singularity

§1.Introduction

Let T be a time scale(nonempty closed subset of R)and[a,b]Tis subset of T such that [a,b]T={t∈T:a≤t≤b},with the subspace topology inherited from the Euclidean topology on R.Open intervals and half-open intervals and so on are defined accordingly.In this paper, we consider the existence and uniqueness of solution to the following singular higher order two-point boundary value problem(BVP,in short)with a parameter λ on time scales

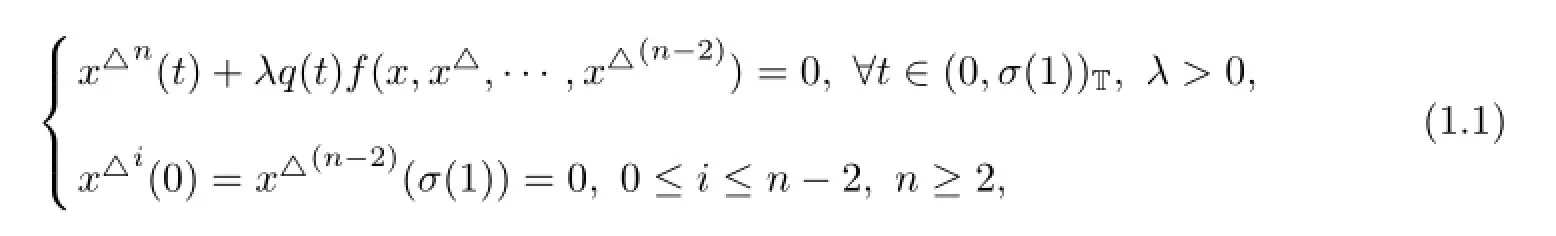
where q(t)∈Crd((0,σ(1))T,(0,+∞)),f∈C((0,+∞)n?1,(0,+∞))and q may be singular at t=0 and/or t=σ(1)and also f may be singular at x=0.

When T=R,in particular,then BVP(1.1)is the following differential equation

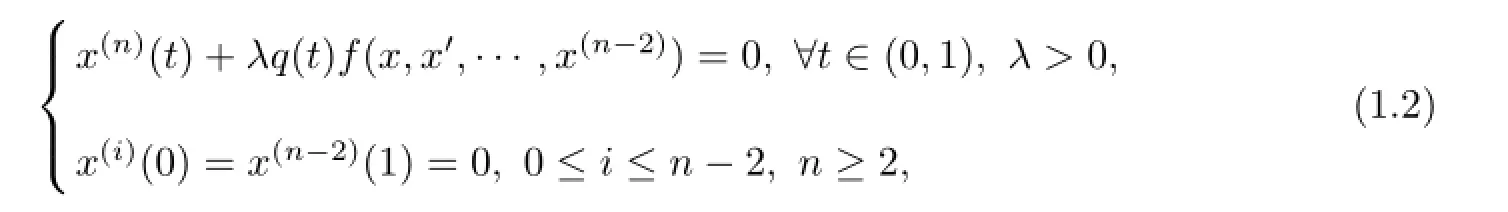
where q(t)∈C((0,1),(0,+∞)),f∈C((0,+∞)n?1,(0,+∞))and q may be singular at t=0 and/or t=1 and also f may be singular at x=0.

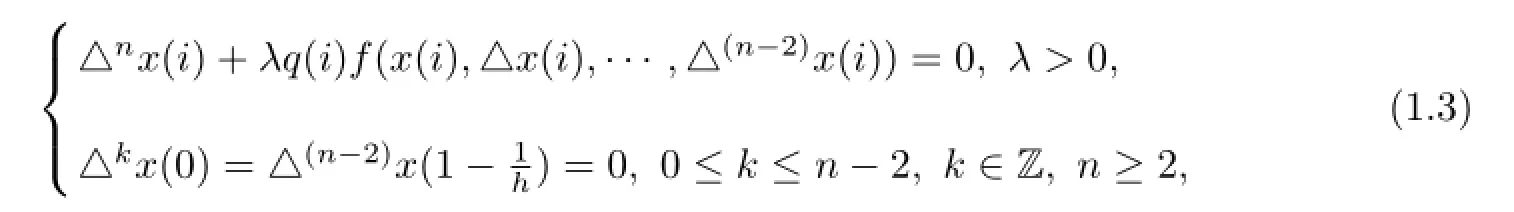
The study of higher order continuous and discrete boundary value problems have been studied extensively in the literature(for example,see[1-5,9]).Most of the results told us that the equations had at least single and multiple positive solutions.Vamsi and Baruah[14]gave bounds for solutions to initial-value problems associated with nonlinear singular interface problems by using the method of upper and lower solutions intertwined with monotone iterative technique.

Time scales can be used in microeconomics models to study behavior which is sometimes continuous and sometimes discrete.A simple example of this continuous-discrete behavior is seen in suppliers’short-run decisions and long-run decisions.Unifying both continuous and discrete model can avoid repeat researches and therefrom we have the capacity to get some different types of models which are neither continuous nor discrete ones that can be effectively described.

Inspired by the paper[15],we dedicated to the research the boundary value problems on time scales.The principle aim of this paper is to systematically study and unify the existence and uniqueness of solutions for the problem(1.1)by ordinary differential equations and their discrete analogues in form of difference equations and to extend these results to more general time scales.In our approach,specifically,we do not deal with a system of classical ordinary differential equations but,more generally,with a system of dynamical equations on time scales. Above,it is a characteristic and innovation of this paper,which differs from the current available literatures.

§2.Preliminaries

In this section,we will give definitions and some lemmas which are useful in proving ourmain results.

Let G(t,s)be the Green’s function for the boundary value problem

which is given by

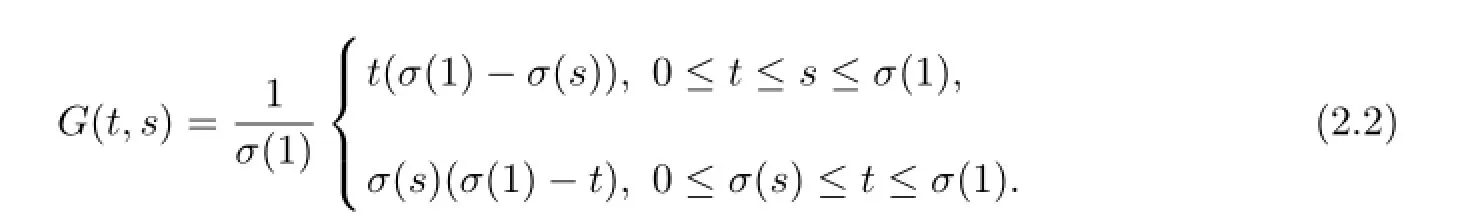
One can show that

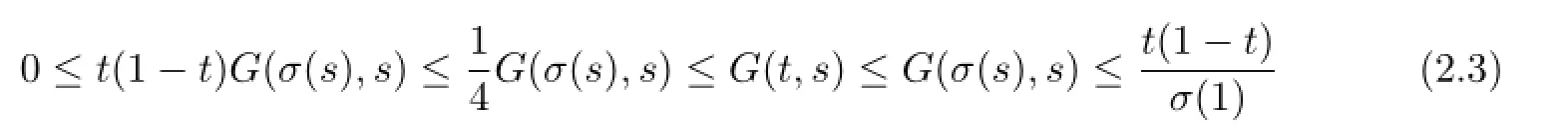
for t∈[0,σ(1)]T.

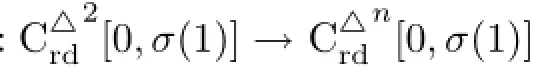
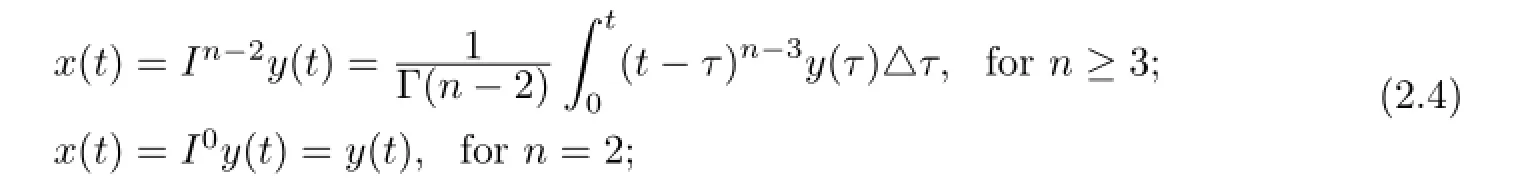
then we have

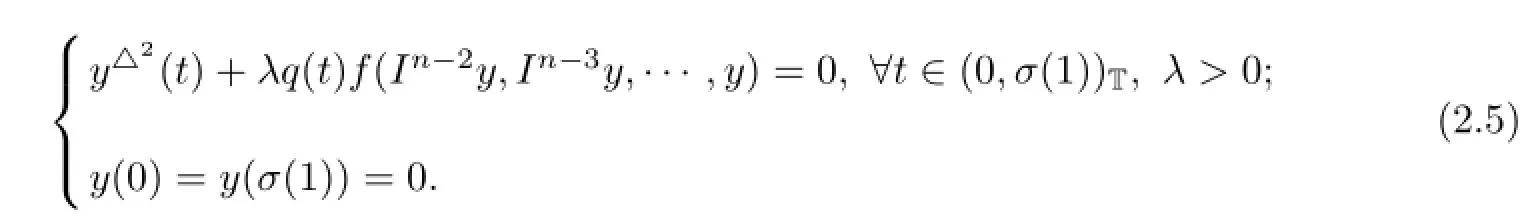
Therefore,if y(t)solves BVP(2.5),then x(t)is a solution to BVP(1.1)by(2.4)and if y(t)is a positive solution of(2.5),then

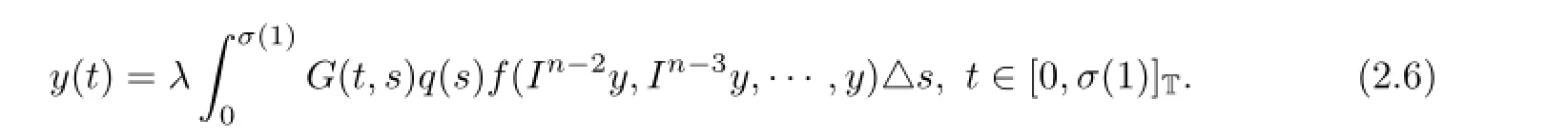
The following definitions and results can be found in[68].

Definition 2.1Let E be a real Banach space.A nonempty closed set K?E is called a cone of E if and only if

(i)a,b∈R,a,b≥0 and x,y∈K implies ax+by∈K;

(ii)x∈K and-x∈K implies x=0.

Given a cone P?E,we define a partial order≤on E with respect to P by x≤y if and only if y-x∈P.We will write x＜y to indicate that x＜y but x/=y,while x?y will stand for y-x∈P?(P?denotes the interior of P).

Definition 2.2A cone P?E is called normal cone if there is a positive number N＞0 such that for all x,y∈E,0≤x≤y implies‖x‖≤N‖y‖.The smallest N is called the normal constant of P.

Let P be a normal cone of Banach space E and e∈P with‖e‖≤1,e/=θ.Define

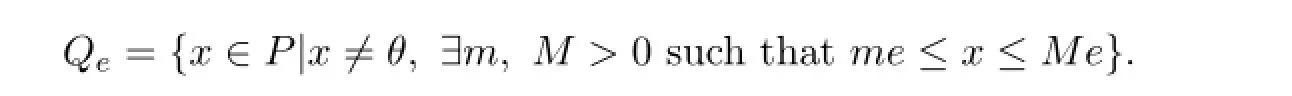
Definition 2.3Assume that A:Qe×Qe→Qe.Now A is said to be mixed monotone if A(x,y)is nondecreasing in x and nonincreasing in y,i.e.,if x1≤x2(x1,x2∈Qe)implies A(x1,y)≤A(x2,y)for any y∈Qeand y1≤y2(y1,y2∈Qe)implies A(x,y1)≥A(x,y2)for any x∈Qe.One says x?∈Qeis a fixed point of A if A(x?,x?)=x?.

Lemma 2.1Assume that A:Qe×Qe→Qeis a mixed monotone operator and there exists a constant α,0≤α＜1,such that

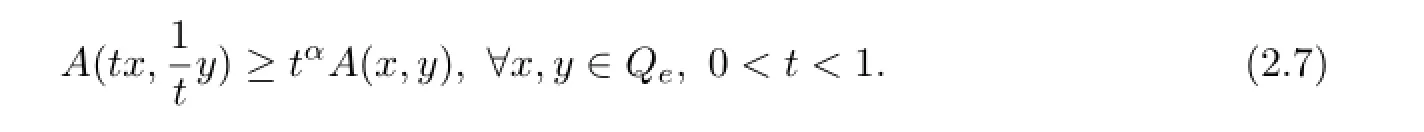
Then A has a unique fixed point x?∈Qe.Moreover,for any(x0,y0)∈Qe×Qe,

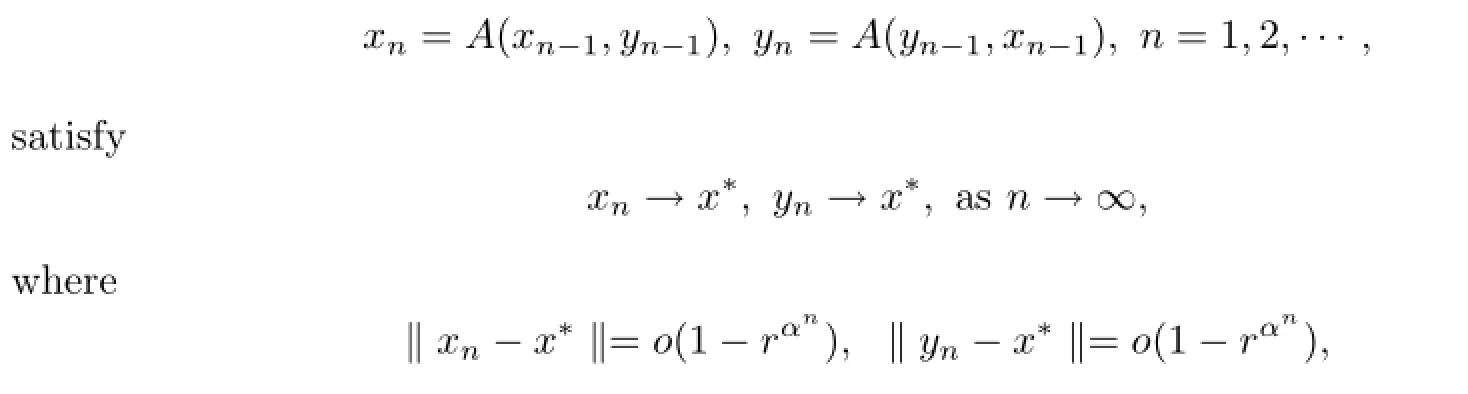
0＜r＜1,r is a constant from(x0,y0).

Lemma 2.2Assume that A:Qe×Qe→Qeis a mixed monotone operator and there exists a constant α∈(0,1)such that(2.7)holds.If x?λis a unique solution of equation

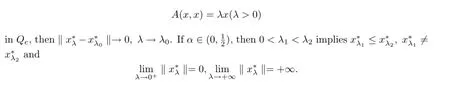
In order to obtain our main results,we also assume that

(A1)f(u1,u2,···,un?1)=g(u1,u2,···,un?1)+h(u1,u2,···,un?1),where

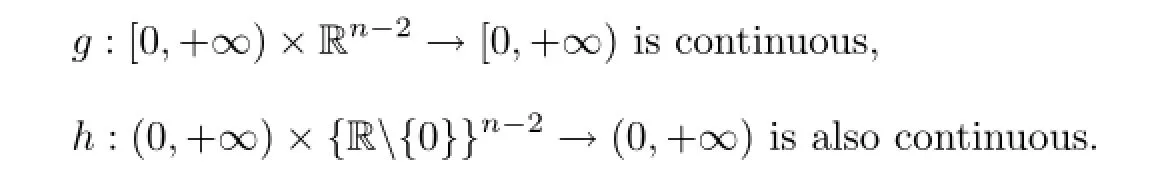
(A2)g is non-decreasing in ui＞0,i=1,2,···,n-1,also h is non-increasing in ui＞0 for i=1,2,···,n-1.

(A3)?α∈(0,1)such that

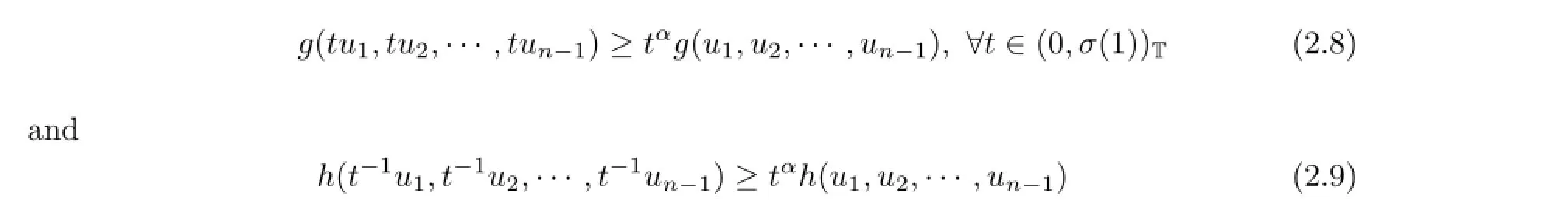
for ui＞0,i=1,2,···,n-1,?t∈(0,σ(1))T.

(A4)q∈Crd((0,σ(1))T,(0,+∞))satisfies

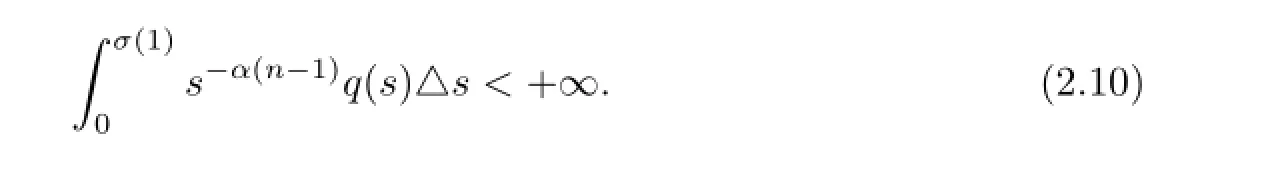
§3.Existence and Uniqueness of Solution

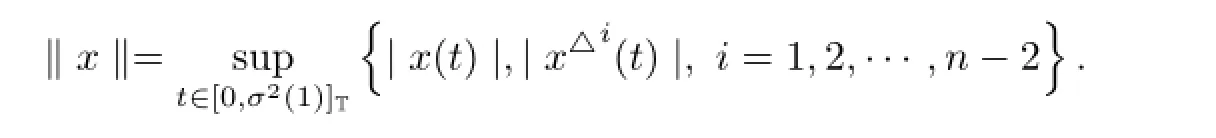
Define a cone by P={x∈E|x(t)≥0,t∈[0,σ(1)]T}and clearly P is a normal cone of the Banach space E.

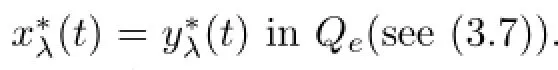
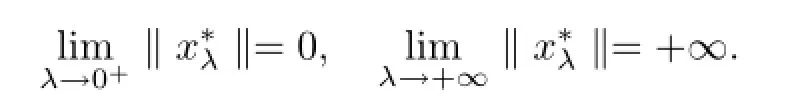
Proof Since(2.9)holds,let t?1ui=vi,i=1,2,···,n-1,one has

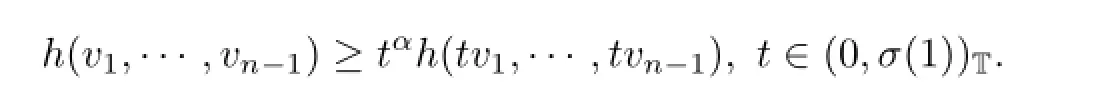
Now with vi=1,i=1,2,···,n-1,there is

From(2.9)and(3.1),one yields

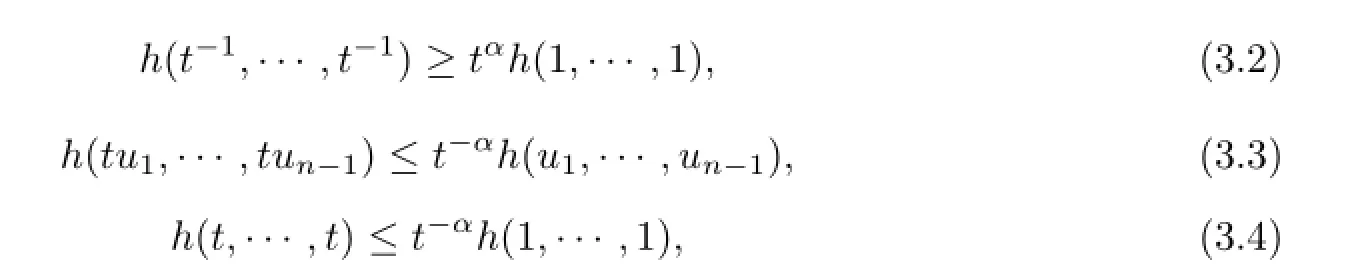
for t∈(0,σ(1)),ui＞0,i=1,2,···,n-1.Similarly,there is

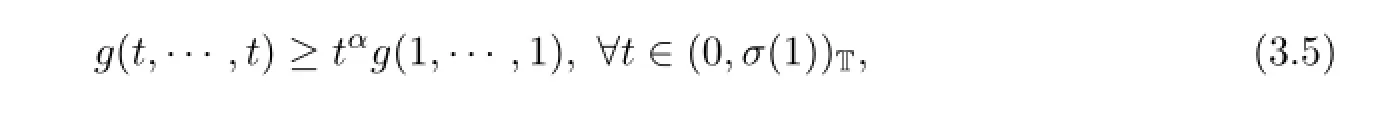
with ui=1,i=1,2,···,n-1,from(2.8).

Now,when u1=u2=···=un?1=:ˉu＞1,let t=ˉu?1,then

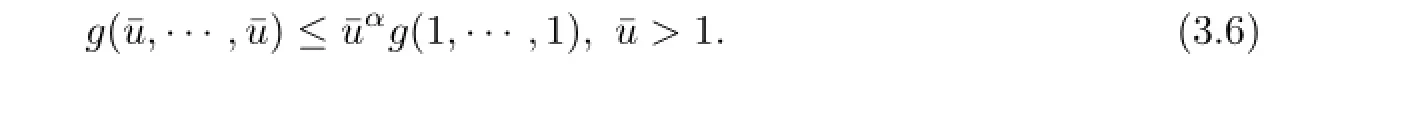
Set e(t):=t(1-t).It is clear that‖e‖≤1 and we define

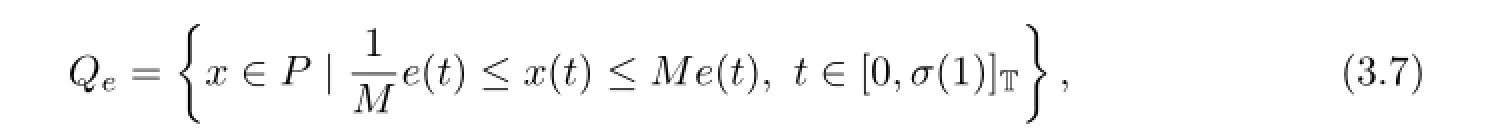
where M＞1 is chosen such that

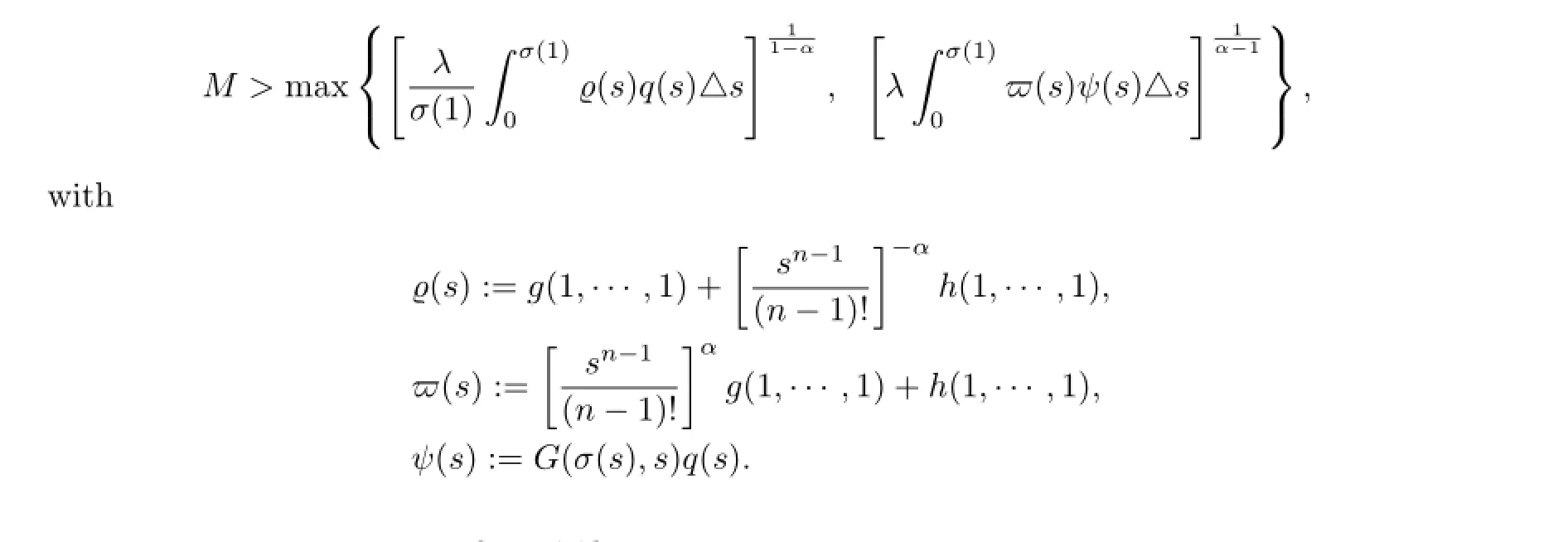
For any v,w∈Qe,?t∈[0,σ(1)]T,now define

First we show that Aλ:Qe×Qe→Qe.Let v,w∈Qe,from(3.6)we have

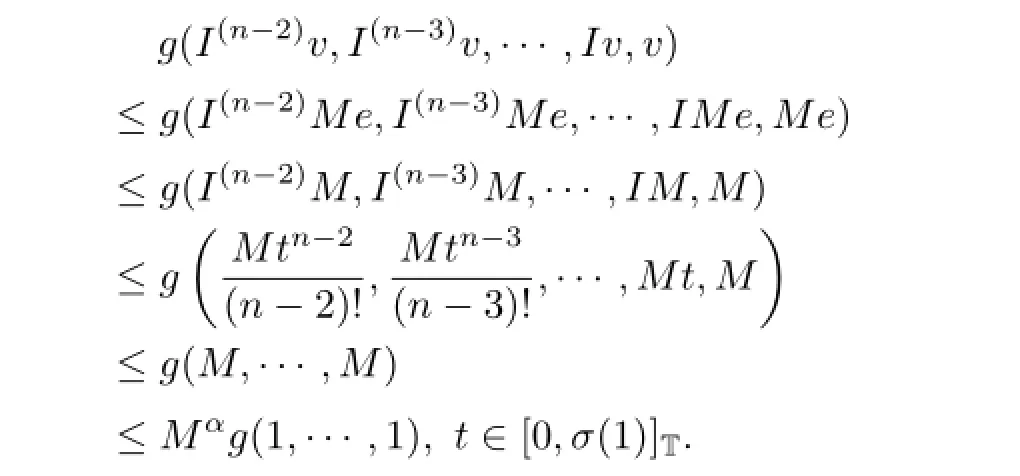
And from(3.3)～(3.4)we obtain

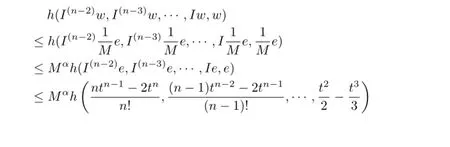
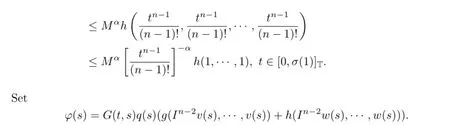
Hence,?t∈[0,σ(1)]T,

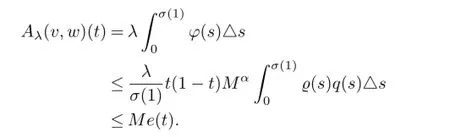
On the other hand,for any v,w∈Qe,by(3.5),we have

Thus we yield

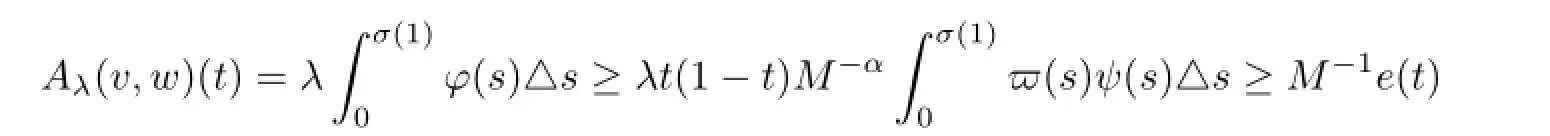
for t∈[0,σ(1)]T.

So,Aλis well defined and Aλ(Qe×Qe)?Qe.Next,?l∈(0,1)and?v,w∈Qe,let

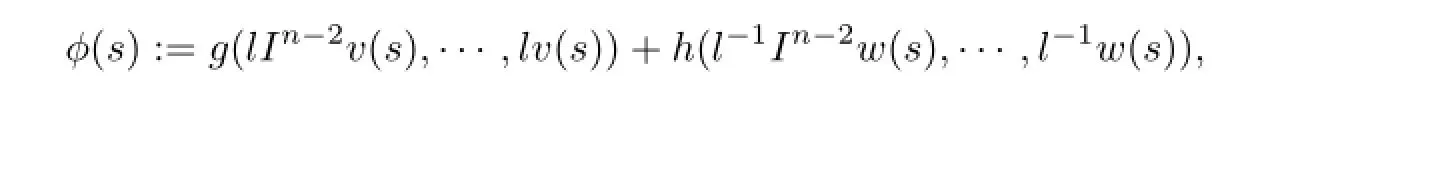
one has

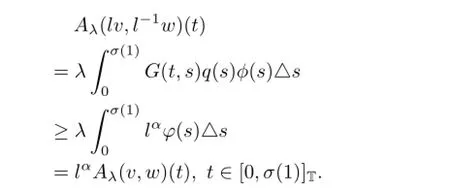
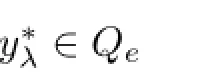
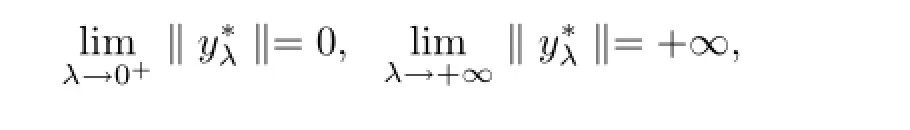
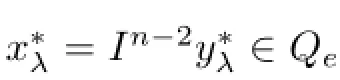
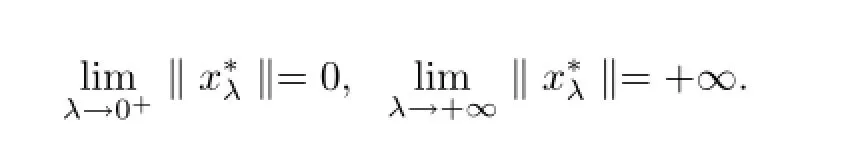
This completes the proof.

§4.Applications

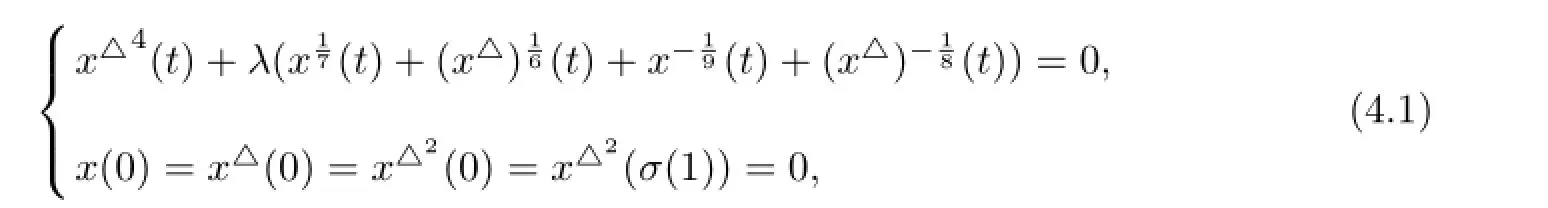
for λ＞0,t∈[0,1]T.

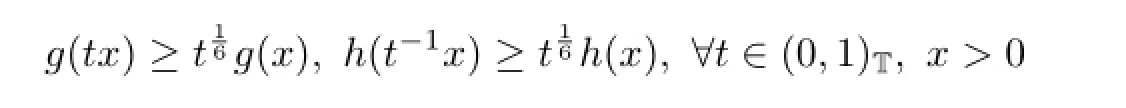
and by calculating directly,we get

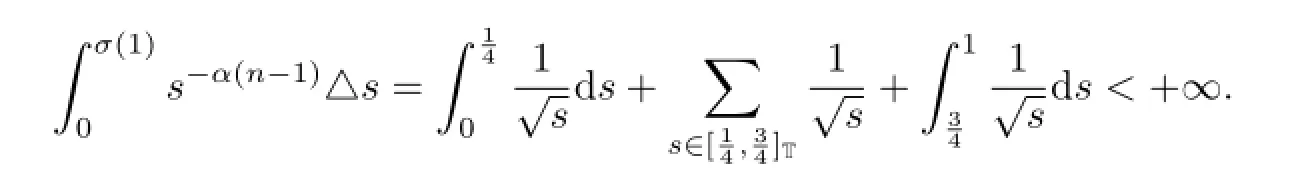
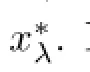
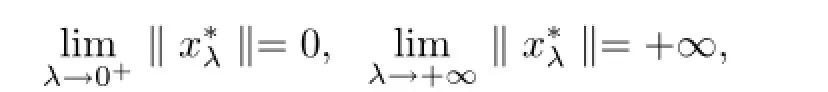
In the same way as in Theorem 3.1,we can obtain the another unique existence result of positive solution to BVP(1.1),under the following assumptions

(A5)f(u1,u2,···,un?1)=g(u1,u2,···,un?1)·h(u1,u2,···,un?1),where

(A6)g is non-decreasing in ui＞0,i=1,2,···,n-1,also h is non-increasing in ui＞0, i=1,2,···,n-1.

(A7)There exist α,β＞0,α+β∈(0,1),such that

for ui＞0,i=1,2,···,n-1,?t∈(0,σ(1))T.

(A8)q∈Crd((0,σ(1))T,(0,+∞))satisfies

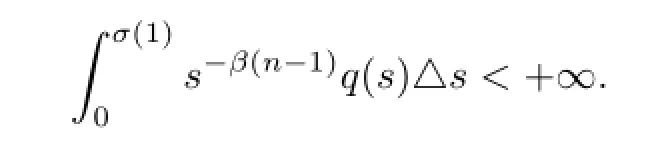
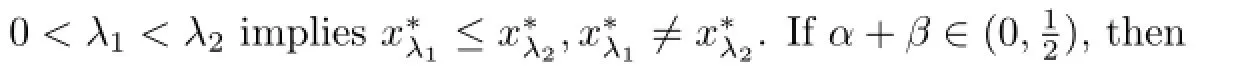
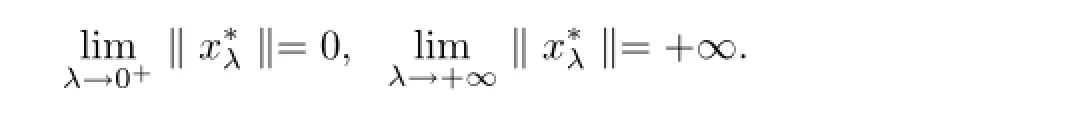
Example 4.2 Consider the following singular boundary value problem

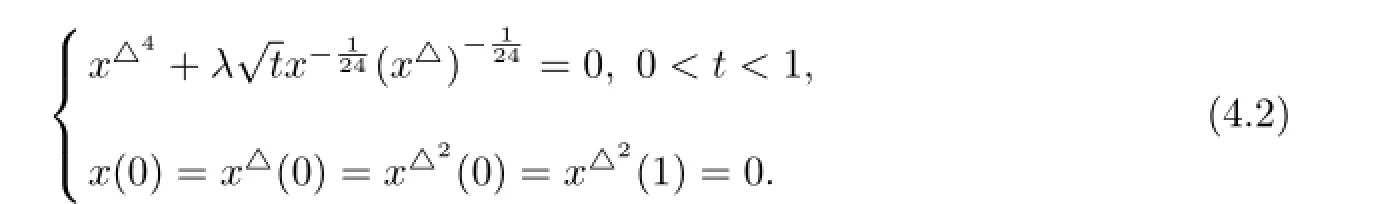
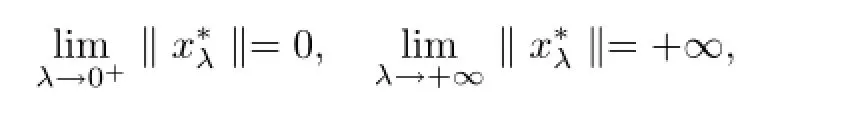
[1]GRAEF J R,YANG Bo.Positive solutions to a multi-point higher order boundary value problem[J].J of Math Anal Appl,2006,316(2):409-421.

[2]GUO Yan-ping,TIAN,Ji-wei.Positive solutions of m-point boundary value problems for higher order ordinary differential equations[J].Nonlinear Analysis,2007,66(7):1573-1586.

[3]JIANG Da-qing,Multiple positive solutions to singular boundary value problems for superlinear higher-order ODEs[J].Acta Math Sci Ser B,2002,22(2):199-206.

[4]AGARWAL R P,O’REGAN D,RACHUNKOVA I,STANEK S.Two-point higher-order BVPs with singularities in phase variables[J].Comput Math Appl,2003,46(12),1799-1826.

[5]AGARWAL R P,WONG Fu-Hsiang.Existence of positive solutions for higher order difference equations[J]. Appl Math Lett,1997,10(5):67-74.

[6]GUO Da-jun,LAKSHMIKANTHAM V.Nonlinear Problems in Abstract Cones[M].Boston:Academic Press,1988.

[7]GUO Da-jun.Partial Order Methods in Nonlinear Analysis[M].Jinan:Shandong Science and Technology Press,2000.

[8]LIN Xiao-ning,JIANG Da-qing,LI Xiao-yue.Existence and uniqueness of solutions for singular fourth-order boundary value problems[J].J of Comput Appl Math,2006,196(1):155-161.

[9]DU Zeng-ji,LIU Wen-bin,LIN Xiao-jie.Multiple solutions to a three-point boundary value problem for higher-order ordinary differential equations[J].J of Math Anal Appl,2007,335(2):1207-1218.

[10]AGARWAL R P,O’REGAN D.Nonlinear superlinear singular and nonsingular second order boundary value problems[J].J of Differential Equations,1998,143(1):60-95.

[11]RAO A K,RAO S N.Multiple positive solutions of boundary value problems for systems of nonlinear second-order dynamic equations on time scales[J].Math Commun,2010,15(1):129-138.

[12]ZHANG Shu-qin.Positive solutions to singular boundary value problem for nonlinear fractional differential equation[J].Comput Math Appl,2010,59(3):1300-1309.

[13]KELLER H B.Existence theory for two point boundary value problems[J].Bull Amer Math Soc,1966, 72(4):728-731.

[14]VAMSI D K K,BARUAH P K.Bounds for solutions of nonlinear singular interface problems on time scales using monotone iterative method[J].Electronic J of Differential Equations,2010,158(15):1714-1717.

[15]LIU Zhen-jie,FANG Xiao-chao,et al.Periodic solutions to a delayed semi-ratio dependent diffusion system on time scales[J].China Quart J of Math,2012,27(2):254-258.

tion:34B16,34B18,34N05

:A

1002–0462(2017)01–0049–10

date:2015-12-12

Supported by the Foundation for Students Innovative Projects of Heilongjiang Province (201510234012)

Biography:TENG Nan(1995-),female,native of Hailun,Heilongjiang,an undergraduate of Harbin University,engages in application and modeling of differential equation.

CLC number:O175.8