[0,1]-拓?fù)淇臻g中T*分離性的非標(biāo)準(zhǔn)分析方法研究

馬春暉, 史艷維, 翟美娟

(1.西安建筑科技大學(xué) 理學(xué)院, 西安 710055; 2.西安培華學(xué)院 基礎(chǔ)部, 西安 710125)

?

[0,1]-拓?fù)淇臻g中T*分離性的非標(biāo)準(zhǔn)分析方法研究

馬春暉1*, 史艷維2, 翟美娟1

(1.西安建筑科技大學(xué) 理學(xué)院, 西安 710055; 2.西安培華學(xué)院 基礎(chǔ)部, 西安 710125)

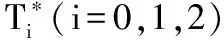
非標(biāo)準(zhǔn)擴(kuò)大模型; 準(zhǔn)分離; 模糊集的鄰域; 模糊集的單子

1 預(yù)備知識(shí)

在一般拓?fù)鋵W(xué)[1]中,許多深刻的結(jié)果都是要求拓?fù)淇臻g具有某種分離性,對(duì)于[0,1]-拓?fù)淇臻g而言,情形也是一樣,因此對(duì)[0,1]-拓?fù)淇臻g中的分離性進(jìn)行深入研究是非常有必要的.自1968年,C. L. Chang[2]以L. A. Zadeh[3]的模糊集理論為骨架創(chuàng)立[0,1]-拓?fù)鋵W(xué)以來(lái),模糊分離性就成為了[0,1]-拓?fù)鋵W(xué)的研究熱點(diǎn)之一.1975年和1977年,B. Hutton先后提出了模糊正則性[4]和模糊完全正則性[5]的概念,這些分離性及其特征刻畫與一般拓?fù)鋵W(xué)中一種傳統(tǒng)的方法是平行的.1980年蒲保明和劉應(yīng)明[6]在研究模糊點(diǎn)的鄰近結(jié)構(gòu)時(shí),基于模糊點(diǎn)的重域,首次提出了準(zhǔn)T0,T0,T1和T2分離性的概念,并對(duì)這些分離性進(jìn)行了系統(tǒng)地討論.之后,王國(guó)俊在文獻(xiàn)[7-8]中利用模糊點(diǎn)的遠(yuǎn)域重建了T分離性.在一般拓?fù)鋵W(xué)中,分離性有多重不同的等價(jià)形式,但在[0,1]-拓?fù)鋵W(xué)中以這些熟知的分離性為藍(lán)本來(lái)建立的模糊分離性卻不等價(jià),于是從不同角度來(lái)推廣一般拓?fù)鋵W(xué)中的同一分離性可以得到不同的模糊分離性.在文獻(xiàn)[7-8]中,王國(guó)俊在T分離性的基礎(chǔ)上,建立了一套系統(tǒng)的T*分離性,這種分離性有別于T分離性,也是一種“好的推廣”(good extension).

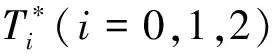
為行文方便,先來(lái)回顧一些非標(biāo)準(zhǔn)分析和[0,1]-拓?fù)鋵W(xué)中的基本概念,詳細(xì)內(nèi)容可以參見(jiàn)文獻(xiàn)[8-11].

如果S≠?滿足以下條件:(1) 對(duì)于任意的x∈S,x≠?;(2) 對(duì)于任意的x∈S,y?x(?y∈S),則稱S是個(gè)體集.對(duì)于個(gè)體集S,歸納定義:

V0(S)=S;Vn+1(S)=Vn(S)∪2Vn(S),

n=0,1,2,…,

定義1設(shè)個(gè)體集S是無(wú)限集,如果映射*:V(S)→V(*S)滿足以下條件:

(1)*?=?;

(2) 對(duì)于任意的s∈S,*s=s;

(3) 轉(zhuǎn)換原理成立,即|=α當(dāng)且僅當(dāng)*|=*α,其中,α是LV(S)中的有界量詞語(yǔ)句,*α是將α中的常量c替換為*c得到的LV(*S)中的有界量詞語(yǔ)句;

(4) 共點(diǎn)原理成立,即對(duì)于任意的V(S)中的共點(diǎn)關(guān)系r,存在y∈V(*S),使得〈*x,y〉∈*r(?x∈dom(r)),

則稱V(*S)是個(gè)體集S的非標(biāo)準(zhǔn)擴(kuò)大模型.

本文總假設(shè)X是無(wú)限集,[0,1]是單位閉區(qū)間,X∪[0,1]?S,且V(*S)是S的非標(biāo)準(zhǔn)擴(kuò)大模型.

關(guān)于模糊點(diǎn)的單子有如下性質(zhì),詳細(xì)的證明可以參見(jiàn)文獻(xiàn)[12].

2 主要結(jié)果

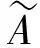
定義4設(shè)(X,δ)是[0,1]-拓?fù)淇臻g,對(duì)于任意X上的模糊點(diǎn)xλ,yμ,當(dāng)xλ與yμ準(zhǔn)分離時(shí):

定理1設(shè)(X,δ)是[0,1]-拓?fù)淇臻g:

證明僅證(3),結(jié)論(1)和(2)類似可證.

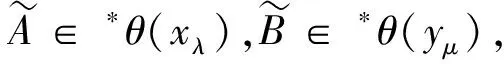
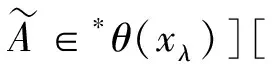
由轉(zhuǎn)換原理可得,如下有界量詞語(yǔ)句在V(S)中成立,

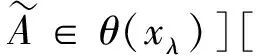
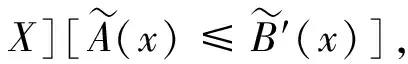
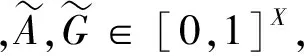
可見(jiàn),模糊集的單子是模糊點(diǎn)的單子的推廣,關(guān)于模糊集的單子,也有類似于引理1的結(jié)論:

證明考慮如下V(S)中的二元關(guān)系

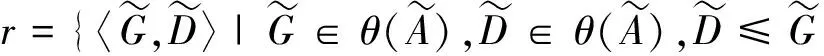
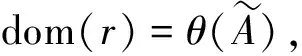
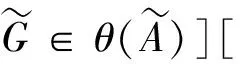
由轉(zhuǎn)換原理可得如下V(*S)中的有界量詞語(yǔ)句成立,

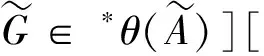
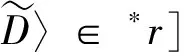
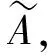
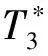
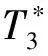
[1]KelleyJL.GeneralTopology[M].NewYork:VanNostrand, 1955.

[2]ChangCL.Fuzzytopologicalspaces[J].JMAA, 1968, 24:182-190.

[3]ZadehLA.Fuzzysets[J].InformationControl, 1965, 8: 338-353.

[4]HuttonB.Normalityinfuzzytopologicalspaces[J].JMAA, 1975, 50:74-79.

[5]HuttonB.Uniformitiesonfuzzytopologicalspaces[J].IBID, 1977, 58:559-571.

[6]PuBaoming,LiuYingming.FuzzytopologyI,NeighborhoodstructureofafuzzypointandMoore-SmithConvergence[J].JMAA, 1980, 76: 571-599.

[7] 王國(guó)俊. 拓?fù)浞肿痈竦姆蛛x公理[J]. 數(shù)學(xué)研究與評(píng)論, 1983, 3(2): 9-16.

[8] 王國(guó)俊.L-Fuzzy拓?fù)淇臻g論[M]. 西安: 陜西師范大學(xué)出版社, 1988.

[9]RobinsonA.NonstandardAnalysis[M].Amsterdam:North-Holland, 1963.

[10]DavisM.AppliedNonstandardAnalysis[M].NewYork:Wiley, 1977.

[11]CutlandNJ.Nonstandardmeasuretheoryanditsapplications[J].BullLondonMathSoc, 1983,15: 529-589.

[12] 馬春暉, 陳東立, 史艷維. [0,1]-拓?fù)淇臻g中的單子及其逼近原理[J]. 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué), 2007, 23(1): 108-111.

A study inT*separations by nonstandard analysis methods in [0,1]-topological spaces

MA Chunhui1, SHI Yanwei2, ZHAI Meijuan1

(1.School of Science, Xi'an University of Architecture and Technology, Xi’an 710055;2.Department of Basic Courses, Xi'an Peihua University, Xi'an 710125)

nonstandard enlarged model; pre-separated; neighborhood of fuzzy set; monad of fuzzy set

2014-10-08.

陜西省自然科學(xué)基金項(xiàng)目(2007A12); 陜西省教育廳專項(xiàng)科研基金項(xiàng)目(2013JK0574); 西安建筑科技大學(xué)人才科技基金項(xiàng)目(RC1239).

1000-1190(2015)02-0167-04

O141.41

A

*E-mail: ma-chunhui@163.com.