Dynamic Anti-plane Crack Analysis in Functional Graded Piezoelectric Semiconductor Crystals

J.SladekV.SladekE.Panand D.L.Young

1　Introduction

Piezoelectric materials(PZ)can be either dielectrics or semiconductors.These materials have been widely used in various electromechanical devices and systems.Up to date dielectric materials are more intensively investigated than semiconductors.However,PZ semiconductors play a crucial role in offering the great electromechanical couling effect within a high-frequency regime.In PZ semiconductors the induced electric field produces also the electric current.The interaction between mechanical fields and mobile charges in PZ semiconductors is called the acoustoelectric effect[Hutson and White(1962);White(1962)].An acoustic wave traveling in a PZ semiconductor can be amplified by application of an initial or biasing dc electric field[Yang and Zhou(2005)].This phenomenon is utilized in many acoustoelectric devices[Heyman(1978);Busse and Miller(1981)].When an acoustic field deforms the PZ material,space charges are generated by the elastic field,causing the electrons to redistribute accordingly.The electron drift induced by an external field can become supersonic,and amplification can take place due to the phonon emission of carriers.

Piezoelectric ceramics are brittle and susceptible to fracture during service.To improve the performance and to predict the reliable service lifetime of ceramic PZ components,it is necessary to analyze theoretically the damage and fracture processes taking place in PZ materials with consideration of the coupling effect between mechanics and electrics.Deeg(1980)and Pak(1990)addressed the inplane and anti-plane fracture problems of an in finite PZ body and obtained the closed form solutions of stress field and electric displacement field near the crack tip.

To meet the demand of advanced PZ materials with improved mechanical,thermal,corrosion and wear resistant properties,the concept of functionally graded materials(FGMs)[Suresh and Mortensen(1998)]has recently been extended to the field of PZ solids.Consequently,the concept of FGMs can be extended to the piezoelasticity to obtain PZ materials with high strength,high toughness,low thermal expansion coefficient and low dielectric constant.Devices such as actuators based on functionally graded PZ materials(FGPMs)are presented by Zhu et al.(1995,1999).Fracture of FGPMs under a thermal load was studied by Wang and Noda(2001).An anti-plane crack problem can be described by relatively simpler governing equations than for in-plane problems[Li and Weng 2002a].The electroelastic problem of an anti-plane shear crack propagating in a functionally graded PZ ceramic strip was analyzed by the integral transform approach[Kwon(2004)].Recently,the in-plane crack problem in FGPMs was analyzed by Chen et al.(2003)and Ueda(2003).Anti-plane cracks in finite functionally graded PZ solids under time-harmonic loading was studied via a non-hypersingular traction based boundary integral equation method[Dineva et al.(2010)].The electrically nonlinear crack problem in a functionally graded PZ ceramic strip was analyzed by Kwon(2003).However,in all these crack problems,the PZ material was considered as a non-conducting dielectric.

There are only few papers devoted to crack problems in PZ semiconductor materials.All papers concern the anti-plane crack problem in unbounded domain with a semi-in finite crack[Yang(2005)]and a finite crack[Hu et al.(2007)]under stationary conditions.The Fourier transform technique is usually applied to reduce the problem to a pair of dual integral equations.In the present paper,we aim at analyzing the anti-plane crack problem in bounded domains with functionally graded material properties and under transient loading conditions.The solution of the boundary value problems for continuously nonhomogeneous PZ solids requires advanced numerical methods due to the high mathematical complexity.The governing equations are more complicated than in a homogeneous counterpart and the electric and mechanical fields are coupled with each other.Transient regime brings additional complications.

In recent years,meshless formulations are becoming popular due to their high adaptivity and low costs to prepare input and output data for numerical analyses.A variety of meshless methods has been proposed so far and some of them are also applied to PZ problems[Ohs and Aluru(2001);Liu et al.(2002);Sladek et al.(2007,2010,2012)].They can be derived either from a weak-form formulation on the global domain or a set of local subdomains.In the global formulation,background cells are required for the integration of the weak-form.The meshless local Petrov-Galerkin(MLPG)method is a fundamental base for the derivation of many meshless formulations,since trial and test functions can be chosen from different functional spaces.Recently,the MLPG method with a Heaviside step function as the test functions[Atluri et al.(2003);Atluri(2004);Sladek et al.(2004);Sladek et al.(2013)]was applied to crack problems in continuously nonhomogeneous medium[Sladek et al.(2007)]and an interface crack problem[Sladek et al.(2010)].Impermeable or permeable crack conditions were considered there.Energetically consistent boundary conditions on the crack-faces are considered too[Sladek et al.(2012)].This model is leading to consistency of total and crack-tip energy release rates.An additional closing traction is added to the well-known semi-permeable crack-face boundary conditions.

In this paper,the MLPG is applied to a finite continuously nonhomogeneous PZ conducting solid with anti-plane crack under transient boundary conditions.The coupled governing partial differential equations for shear stresses,electric displacement field and current are satisfied in a weak-form on small fictitious subdomains.Nodal points are introduced and spread on the analyzed domain and each node is surrounded by a small circle for simplicity,but without loss of generality.If the shape of subdomains has a simple form,numerical integrations over them can be easily carried out.The integral equations have a very simple nonsingular form.The spatial variations of the displacement,electric potential and electron density are approximated by the Moving Least-Squares(MLS)scheme[Zhu et al.(1998)].After performing the spatial integrations,a system of ordinary differential equa-tions for unknown nodal values is obtained.The essential boundary conditions on the global boundary are satisfied by the collocation approach.Then,the system of the ordinary differential equations of the second order resulting from the equations of motion is solved by the Houbolt finite-difference scheme[Houbolt 1950]as a time-stepping method.

2　Local integral equations for piezoelectric semiconductor

Consider a homogeneous n-type PZ semiconductor withm0electron density in unloaded state with vanishing initial electric fieldE0.Supposing the frequency of external loadings to be close to characteristic frequency of elastic waves,one can assume quasi-static approximation for the electromagnetic field.Then,the effect of Faraday’s induction is neglected even if there is a magnetic field induced by the electric current according to the Ampere’s law.Eventually,the governing equations within the linear theory are given by the balance of momentum,Gauss’s law and conservation of charge[Hutson and White(1962)]

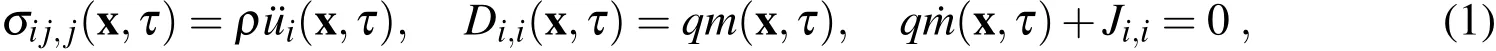
where¨ui,σij,Di,andqare the acceleration of displacements,stress tensor,electric displacement field,and electric charge of the electron,respectively.The electron density and electric current are denoted bymandJi,respectively.Symbolρis used for the mass density.A comma followed by an index denotes partial differentiation with respect to the coordinate associated with the index.

These governing equations(1)have to be supplemented by the constitutive equations below[Hutson and White(1962);White(1962)]

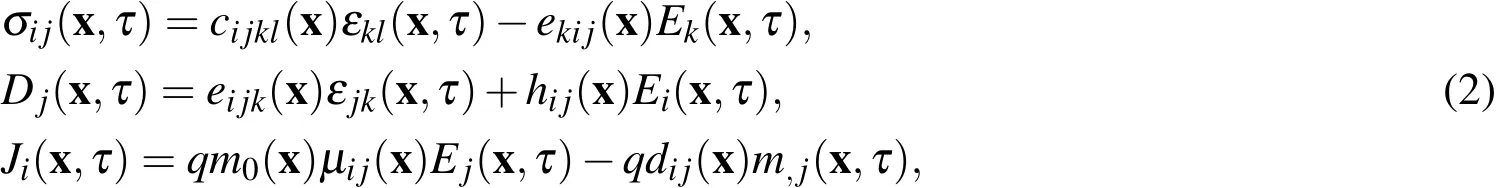
wherecijkl(x),eijk(x),hij(x),μij(x)anddij(x)are the elastic,PZ,dielectric,electron mobility and carrier diffusion material coefficients,respectively.Generally,these coefficients can depend on Cartesian coordinates in functionally graded materials.

Finally,the strain tensorεijand the electric field vectorEjare related to the displacementsuiand the electric potentialφby

In this analysis,we assume a transversely isotropic PZ solid.Assuming anti-plane deformations(u1=u2=0)with all the fields dependent on the in-plane coordinates(x1,x2),hence the following fields vanish:

Then,the governing equations are transformed into a simpler form

The constitutive equations for the transversally isotropic anti-plane problem become[Hu et al.(2007)]

Instead of writing the global weak-form for the above governing equations,we apply the MLPG method to construct a weak-form on the local fictitious subdomains such as ?s,which is a small region taken for each node inside the global domain[Atluri(2004)].The local subdomains are distributed inside the whole global domain ?.The local subdomains could be of any geometrical shape and size.In the present paper,the local subdomains are taken to be of circular shape.The local weak-form of the governing equations(5)can be written as

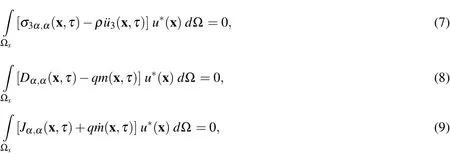
whereu?(x)is a test function.

Applying the Gauss divergence theorem to equations(7)-(9)one obtains

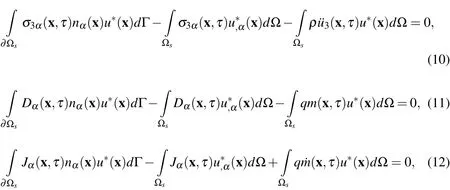
where??sis the boundary of the local subdomain[Atluri 2004]andnαis a unit normal vector to the boundary??s.By choosing a Heaviside step function as the test functionu?(x)in each subdomain

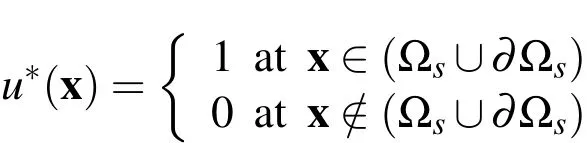
the local weak-forms(10)-(12)are converted into the following local boundarydomain integral equations

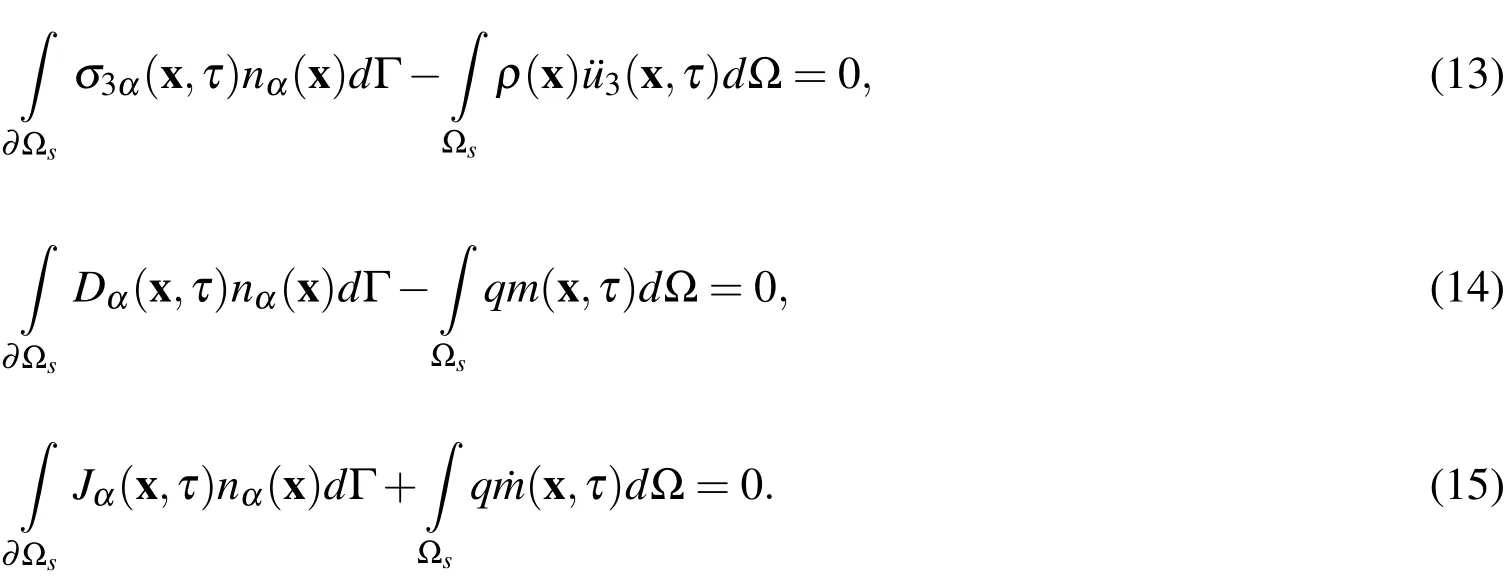
In the MLPG method the test and trial functions are not necessarily from the same functional spaces.For internal nodes,the test function is chosen as the Heaviside step function with its support on the local subdomain.The trial functions,on the other hand,are chosen to be the moving least-squares(MLS)approximation over a number of nodes spread within the domain of influence.Details are given in the next section.

3　Numerical solution

According to the MLS[Lancaster and Salkauskas(1981);Nayroles et al.(1992)]method,the approximation of physical fieldsf(x,τ)(i.e.,the displacement,electric potential and electron density)over a number of randomly located nodes=1,2,...n,is given by

wherenis the number of nodes used for the approximation.It is determined by the weight functionwa(x)associated with the nodea.The symbolstands for the fictitious nodal values,but not the nodal values of the unknown trial functions in general.The stationarity ofsin eq.(19)with respect to a(x,τ)leads to the following linear relation between a(x,τ)and

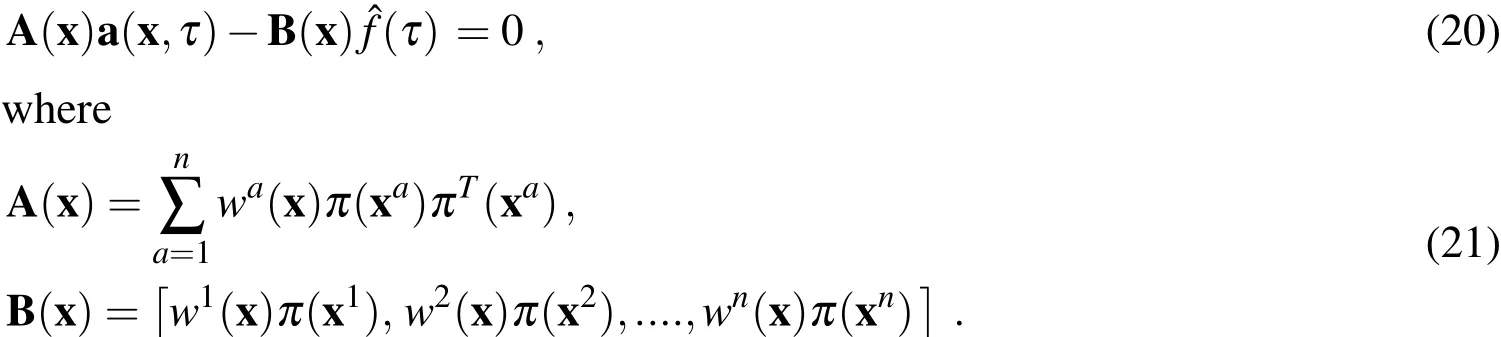
The solution of Eq.(20)for a(x,τ)and a subsequent substitution into Eq.(16)gives the approximation formulas for the displacement,electric potential,and electron density[Sladek et al.(2010)]

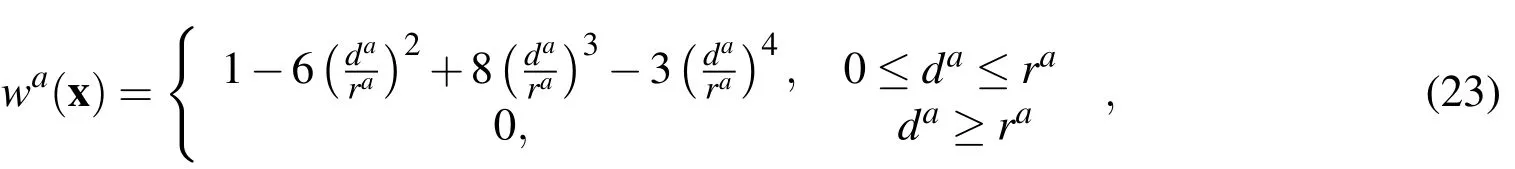
whereis the size of the support domain.It is seen that theC1-continuity is ensured over the entire domain;therefore the continuity conditions of the traction,electric charge and the electric current are satisfied.

In the local integral equations(13)-(15)we have the scalar products of the normal vector with shear stresses,electrical displacement and electric current.Substituting the MLS approximations into the scalar products we obtain

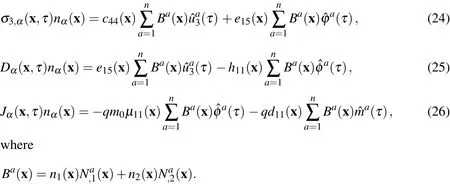
Substituting Eqs.(24)-(26)into the local integral equations(13)-(15),we obtain the following system of ordinary differential equations

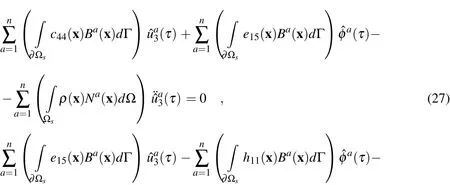
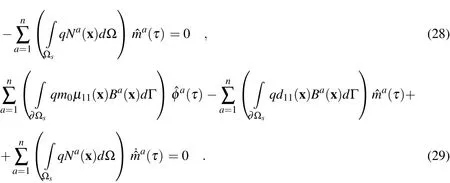
The essential boundary conditions at nodal points on the global boundary are satisfied by approximation formula(22)

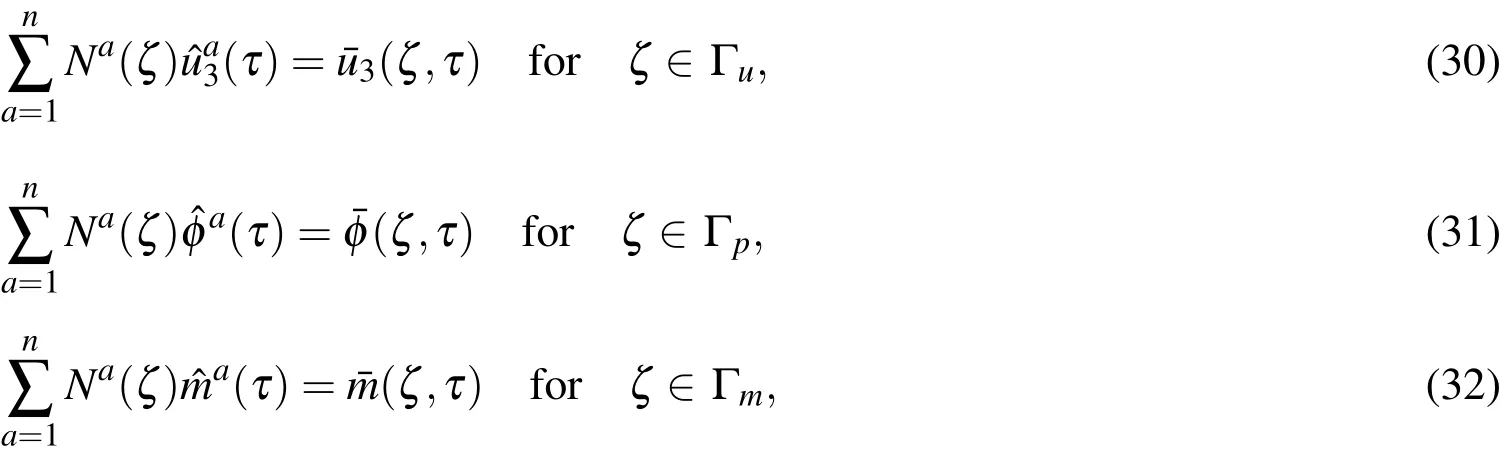
It should be noted that one of the most important properties of the MLS approximation is its high-order continuity of approximated fields.On the other hand,there are such problems in which even the primary fields suffer certain discontinuities.For instance,the displacements are discontinuous across the crack surface.Crack discontinuities can be treated in several ways in the meshless approximation[Organ et al.(1996);Carpinteri et al.(2003)].The simplest approach to satisfy the discontinuity of displacements on the crack surfaces is the visibility criterion.Nodes lying inside the domain ABC shown in Fig.1 are not considered for the evaluation of the shape function at the point x in the MLS-approximation(i.e.,the mentioned nodes are excluded from the support domain).Another approach for the treatment of crack discontinuities in both the meshless and the FEM is based on the introduction of discontinuous enrichment functions[Belytschko et al.(2001)].Carpinteri et al.(2003)proposed the method where the crack is virtually extended in the direction of the tangent at the crack-tip.All the weight functions whose support domains intersect the real crack are cut along the crack line(real+virtual),while the weight functions are left unchanged if the support domains intersect only the virtual crack.That method has to be applied to problems where symmetry with respect to the crack plane cannot be utilized and both crack surfaces has to be modeled.It happens if materials properties are varying along the direction normal to the crack plane.

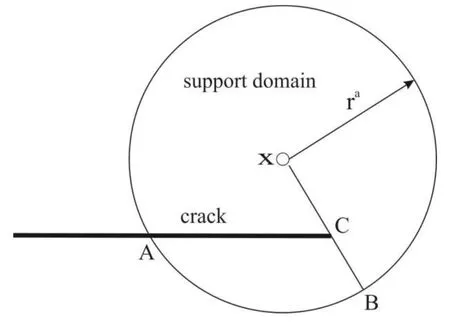
Figure 1:Visibility criterion for the support of domain in the crack-tip vicinity.

4　Numerical examples

Consider a finite PZ semiconductor strip in planex1-x2with size 2H×2L(Fig.2)and a central crack with length 2a.On the top and bottom surfaces,the shear stressτ0,electric displacementD0and the electric currentJ0are applied.Electrically impermeable boundary conditions on the crack surface are considered that gives rise to singular behavior of both the electric intensity and electric displacement fields near the crack tips.First,the numerical analysis is performed for a homogeneous material.The material properties correspond to Cadmium Sulfide CdS[Auld 1973]:

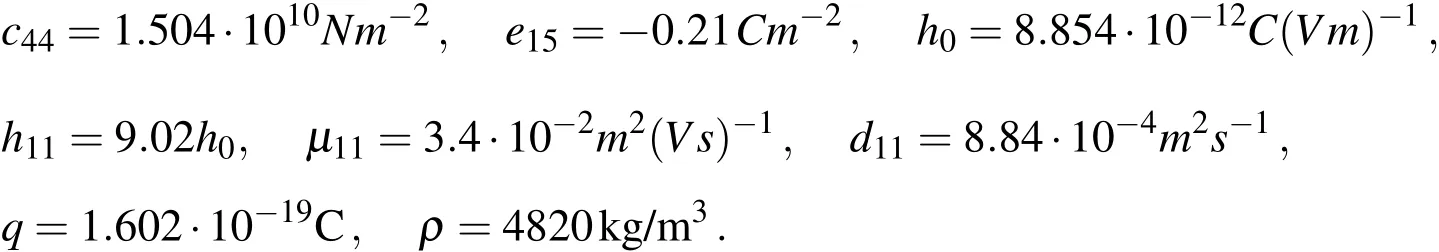
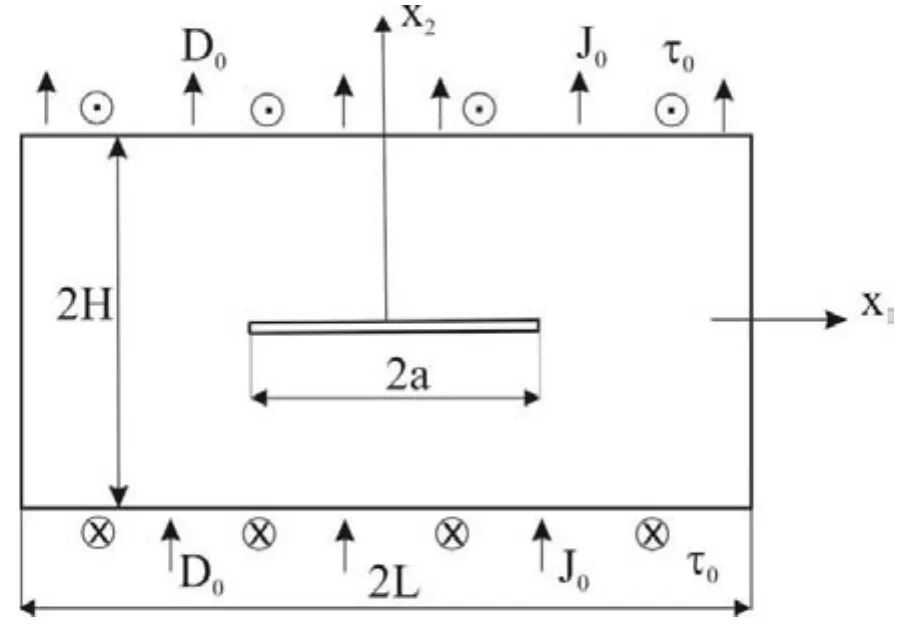
Figure 2:Anti-plane crack in a finite strip.

Due to the symmetry of the problem,it is sufficient to analyze only a quarter of the cracked strip.The strip widthL=2.5a,crack lengtha=0.08mand height of the striph=1.25Lare considered.In the first example the crack size is relatively small with respect to the strip size.The mechanical displacement,electrical potential and electron density in the quarter of the specimen are approximated with 930(31x30)nodes equidistantly distributed.The local subdomains are considered to be circular with a radiusrloc=0.006m.

Variations of displacements,electric potentials and electron densities along the crack surface for various initial electron densitiesm0are presented in Figs 3,4 and 5,respectively.The presented numerical results correspond to a pure mechanical loadτ0=1Pa.One can observe that initial electron density has a small influence on the crack displacement.However,the induced electric potential is strongly dependent on the initial electron density.The largest value of the induced potential is for a non-conducting PZ material.With increasing value ofm0,the induced electric potential decreases.The observed electron density on the crack surface is strongly dependent onm0value.The higher value ofm0results in lower density of electronsm.

For cracks in homogeneous and linear PZ solids the asymptotic behaviour of the field quantities near the crack tip has been given by Sosa(1991)and Pak(1992).In one of our previous papers[Sladek et al.(2007)]we showed that the stress singularity at the crack tip in a continuously nonhomogeneous PZ solid is the same as that in a homogeneous one.Therefore,similarly to a homogeneous case[Hu et al.,(2007)]we can de fine field intensity factors in functionally graded PZ semiconductors as

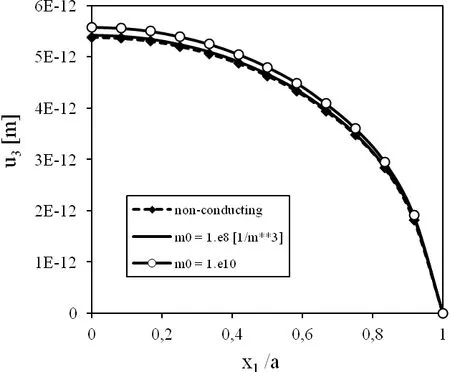
Figure 3:Variation of displacement u3along the crack under a pure mechanical load τ0=1N/m2.

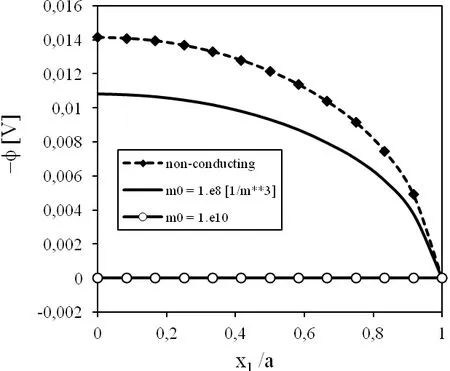
Figure 4:Variation of the electric potential(-φ)along the crack under a pure mechanical load τ0=1N/m2.

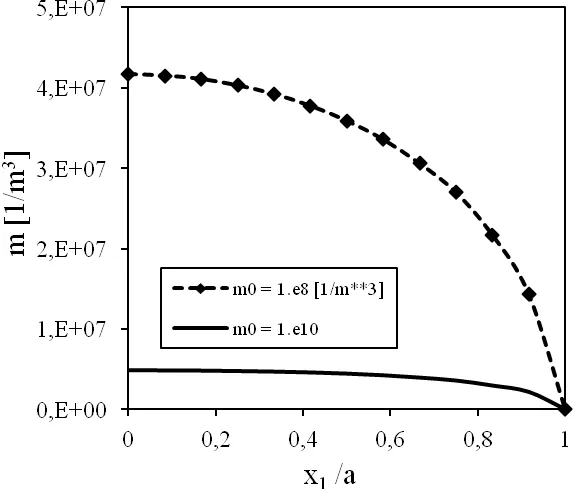
Figure 5:Variation of the electron density m along the crack under a pure mechanical load τ0=1N/m2.

whereare the stress intensity factor,electrical displacement intensity factor,strain intensity factor and electric field intensity factor,respectively All intensity factors(IFs)in equations(33)-(36)are computed using the extrapolations technique from three corresponding quantities at three points ahead the crack tip.Their distance from the crack tip has to be sufficiently small due to validity of asymptotic expansion of stressσ23,electric displacementD2,strainγ23and electric intensity fieldE2.It follows from constitutive equations(2)and(6)that intensity factorsKσandKDcan be expressed byKγandKE,respectively.Then,one gets

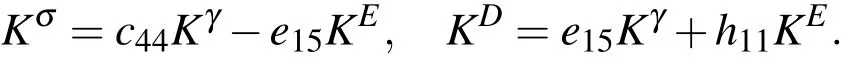
The energy release rate can be de fined on the base of above given intensity factors[Pak(1990)]

For stationary boundary conditions the stress intensity factor(SIF)for nonconducting PZ solid is independent on electric loadD0.The SIF vanishes in such a case since the stressesσ23are zero ahead the crack tip on the crack line because of the immediate electromechanical interaction,despite the finite value of induced electric potential for a pure mechanical load(Fig.4).It means that displacement and electric potential are coupled;however,intensity factors are decoupled in a stationary case.

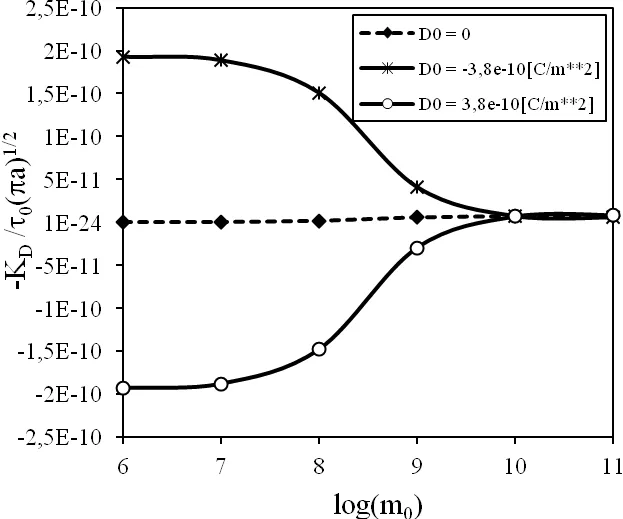
Figure 6:Variation of the electric displacement intensity factor with initial electron density.

In conducting PZ solids we observe a strong influence of the initial electronic densitym0on the induced electric potential.Therefore,it is interesting to investigate the influence ofm0on the electric displacement intensity factor for the crack under a mixed mechanicalτ0and electric loadD0.The variation ofKDwith initial electron density is given in Fig.6.For a pure mechanical load we get a vanishing value ofKDfor any value ofm0.For a finite value of the electric loadD0we get a finite value ofKDfor non-conducting material.With increasing conductivity of PZ semiconductor,theKDvalue is reduced and form0=1011m-3the electric displacement intensity factor is almost zero.

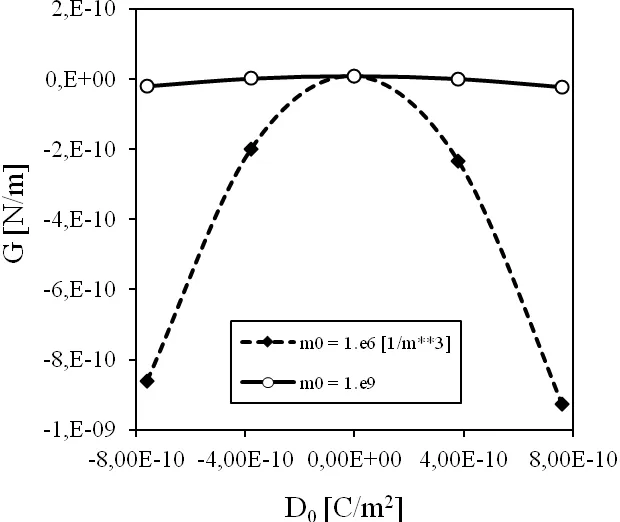
Figure 7:Influence of the electric load on the energy release rate for a mixed load.

The influence of the electric loadD0and electric currentJ0on the energy release rate is shown in Fig.7 and 8,respectively.Two different initial electron densities are considered in the numerical analyses.One can observe that the energy release rate is less sensitive on the electric load and electric current for PZ semiconductor as for non-conducting PZ solid,since the initial electron densitym0=106can be considered as a value corresponding to a non-conducting solid.

It is also interesting to investigate influence of the geometry(crack size and strip size)on G.Therefore,we consider a larger crack with lengtha=0.08mand smaller strip heighth=1.0Land strip widthL=2.0a.The energy release rate for this cracked specimen is givenin Fig.9.The sensitivity on the electric current is smaller for a larger crack size and smaller specimen.A similar influence is observed for the electric loadD0as shown in Fig.10.

We now consider the influence of the non-stationary boundary conditions on the physical quantities.The strip is subjected to an impact load with Heaviside time variation and the intensityτ0=1Pafor a pure mechanical load.Time variation of the normalized stress intensity factors for a non-conducting and semiconductor PZ solid are presented in Fig.11,whereOne can observe that the initial electron density has vanishing influence on the SIF.In non-stationary case a pure electrical load can induce finite value of the SIF.The response of the electric fields is immediate,while that of the elastic ones is taken as finite because of the finite velocity of elastic waves.On the other hand,in a static case,the response of both the mechanical(strain,stress)and electrical fields is immediate.One can observe finite value of the electric displacement intensity factor(EDIF)for a pure mechanical load in Fig.12.However,due to small value of the PZ coefficient,the induced EDIF is small for non-conducting solid.Larger values are observed for the conducting material.It is due to strong influence ofm0onKDas observed for stationary boundary conditions.

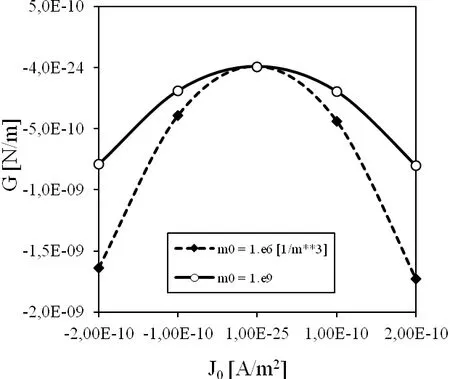
Figure 8:Influence of the electric current on the energy release rate for a mixed load.

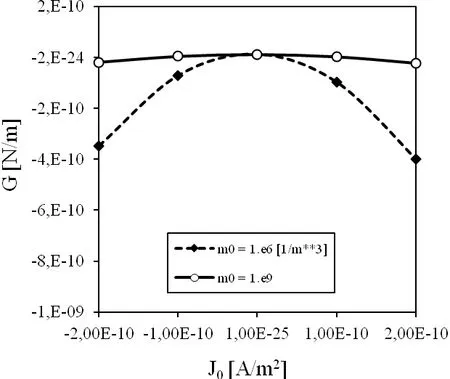
Figure 9:Influence of the electric current J0on the energy release rate for a mixed load when the crack is larger with a=0.1m.

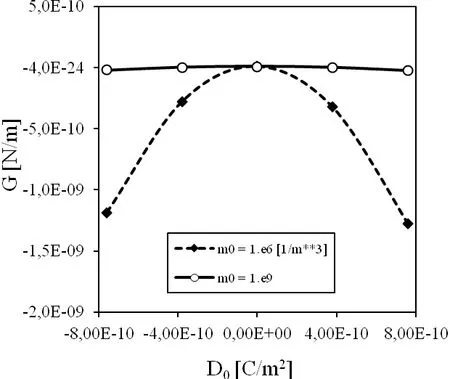
Figure 10:Influence of the electric load D0on the energy release rate for a mixed load when the crack is larger with a=0.1m.

If a pure electric loadD0is applied one can observe a strong influence ofm0on the SIF as shown in Fig.13.Larger values of the SIF are achieved in non-conducting PZ material.The time variation of the normalized EDIF is presented in Fig.14.For both conducting and non-conducting materials the EDIF in the whole time interval is almost uniform.A larger reduction of the EDIF is observed for conducting PZ material.

Finally,we consider the functionally graded material(FGM)properties for the shear modulusc44inx2coordinate.An exponential variation is used

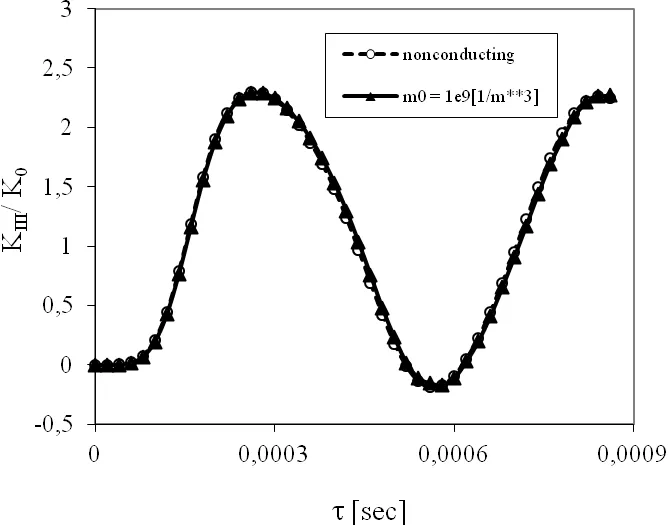
Figure 11:Normalized stress intensity factor for the anti-plane crack within a strip under a pure mechanical load τ0.

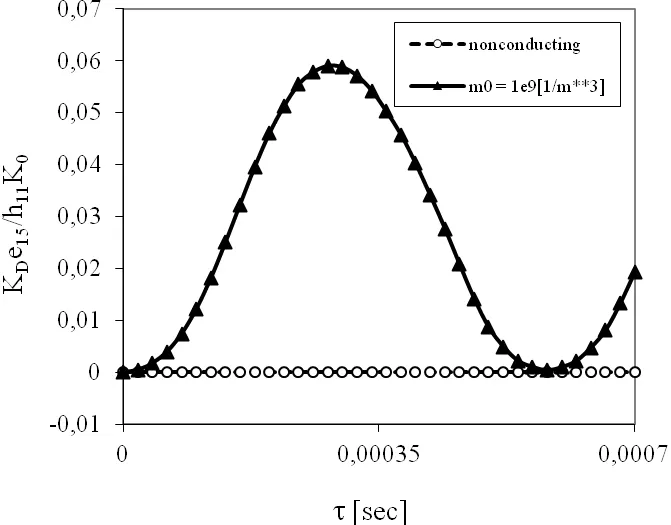
Figure 12:Normalized EDIF for the anti-plane crack within a strip under a pure mechanical load τ0.

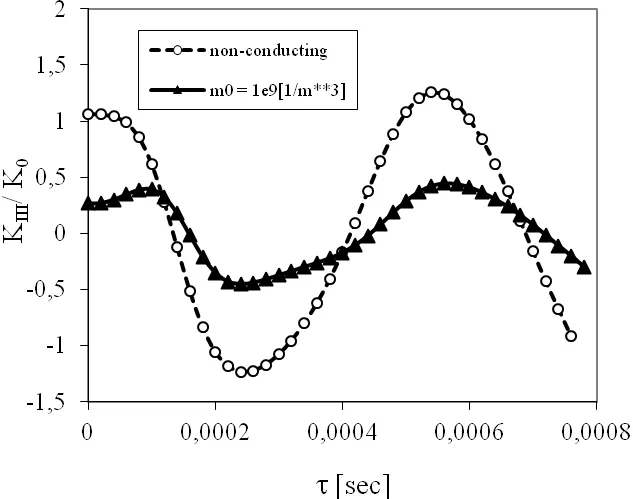
Figure 13:Normalized SIF for the anti-plane crack within a strip under a pure electric load D0=0,38·10-10C/m2.

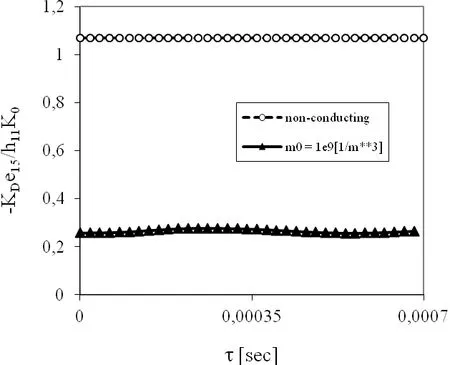
Figure 14:Normalized EDIF for the anti-plane crack within a strip under a pure electric load D0=0,38·10-10C/m2.

wherec440corresponds to material parameter used in the previous example.For considered geometry and material gradation the shear modulus is almost doubled on the top and bottom surfaces than in the crack plane.Other material parameters are uniform with values given in earlier examples.A pure impact load with Heaviside time variation and initial electron densitym0=109m-3are considered.Numerical results for normalized stress intensity factor are presented in Fig.15.

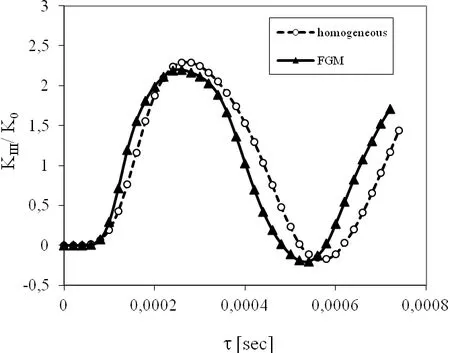
Figure 15:Influence of the shear modulus gradation on the SIF in a cracked strip under a pure mechanical impact load with m0=109m-3.

For a gradation of mechanical material properties withx2coordinate and a uniform mass density,the wave propagation grows withx2.Therefore,the peak value of the SIF is reached in a shorter time instant in FGM strip than in a homogeneous one.The maximum value of the SIF is only slightly reduced for the FGM cracked strip.

5　Conclusions

The meshless local Petrov-Galerkin method(MLPG)is developed for transient dynamic analyses of the anti-plane crack problem in continuously nonhomogeneous PZ semiconductors.The analyzed 2-D domain of arbitrary shape is divided into small subdomains for which local integral equations are derived.The moving least-squares(MLS)scheme is adopted for approximating the physical quantities.The numerical results revealed that initial density of electrons(carriers of electric charge in n-type PZ semiconductors)has a strong influence on the induced electric potential and electric displacement intensity factor(EDIF).With increasing electric current in PZ semiconductor,the EDIF is decreasing.It has been observed that energy release rate is less sensitive to the electric load and electric current for PZ semiconductor as for non-conducting PZ solid.The influence of the ratio of crack length to the specimen size on the energy release rate is investigated too.The sensitivity of the energy release rate on the electric current and electric load decreases with increasing crack length ratio.

One can observe that the initial electron density has vanishing influence on the stress intensity factor(SIF)for a crack under a pure impact mechanical load.In non-stationary case a pure electrical load yields a finite value of the SIF.More distinct response is observed in non-conducting material than in the PZ semiconductors.The normalized EDIF is almost invariable in time for both the conducting and non-conducting PZ samples.The EDIF for conducting PZ material,however,is significantly lower than that for the non-conducting PZ material.

Acknowledgement:The authors gratefully acknowledge the supports by the Slovak Science and Technology Assistance Agency registered under number APVV-0014-10 and the Slovak Grant Agency VEGA-2/0011/13.

Atluri S.N.(2004):The Meshless Method,(MLPG)For Domain&BIE Discretizations,Forsyth,Tech Science Press.

Atluri,S.N.;Han,Z.D.;Shen,S.(2003):Meshless local Petrov-Galerkin(MLPG)approaches for solving the weakly-singular traction&displacement boundary integral equations.CMES:Computer Modeling in Engineering&Sciences,vol.4,no.5,pp.507-516.

Auld,B.A.(1973):Acoustic Fields and Waves in Solids.John Wiley and Sons,New York,pp.357-382.

Belytschko,T.;Moes,N.;Usi,S.;Parimi,C.(2001):Arbitrary discontinuities in finite elements.Int.J.Num.Meth.Eng.,vol.50,pp.993-1013.

Deeg,W.F.(1980):The analysis of dislocation,crack,and inclusion problems in piezoelectric solids.Ph.D.Thesis,Stanford University,Stanford,CA.

Busse,L.J.;Miller,J.G.(1981):Response characteristics of a finite aperture,phase insensitive ultrasonic receiver based upon the acoustoelectric effect.J.A-coust.Soc.Am.,vol.70,pp.1370-1376.

Carpinteri,A.;Ferro,G.;Ventura,G.(2003):The partition of unity quadrature in element-free crack modeling.Comput.Struct.,vol.81,pp.1783-1794.

Chen,J.;Liu,Z.X.;Zou,Z.Z.(2003):Electromechanical impact of a crack in a functionally graded piezoelectric medium.Theoretical and Applied FractureMechanics,vol.39,pp.47-60.

Dineva,P.;Gross,D.;Muller,R.;Rangelov,T.(2010):BIEM analysis of dynamically loaded anti-plane cracks in graded piezoelectric finite solids.Int.J.Solids Structures,vol.47,pp.3150-3165.

Heyman,J.S.(1978):Phase insensitive acoustoelectric transducer.J.Acoust.Soc.Am.,vol.64,pp.243-249.

Houbolt,J.C.(1950):A recurrence matrix solution for the dynamic response of elastic aircraft.Journal of Aeronautical Sciences,vol.17,pp.371-376.

Hu,Y.;Zeng,Y.;Yang,J.(2007):A mode III crack in a piezoelectric semiconductor of crystals with 6mm symmetry.Int.J.Solids Structures,vol.44,pp.3928-3938.

Hutson,A.R.;White,D.L.(1962):Elastic wave propagation in piezoelectric semiconductors.J.Appl.Phys.,vol.33,pp.40-47.

Kwon,S.M.(2004):On the dynamic propagation of an anti-plane shear crack in a functionally graded piezoelectric strip.Acta Mechanica,vol.167,pp.73-89.

Kwon,S.M.(2003):Electrical nonlinear anti-plane shear crack in a functionally graded piezoelectric strip.Int.J Solids Structures,vol.40,pp.5649-5667.

Lancaster,P.;Salkauskas,K.(1981):Surfaces generated by moving least square methods.Math.Comput.,vol.37,pp.141-158.

Li,C.;Weng,G.J.(2002):Antiplane crack problem on functionally graded piezoelectric materials.ASME Journal of Applied Mechanics,vol.69,pp.481-488.

Liu,G.R.;Dai,K.Y.;Lim,K.M.;Gu,Y.T.(2002):A point interpolation mesh free method for static and frequency analysis of two-dimensional piezoelectric structures.Comput.Mech.,vol.29,pp.510-519.

Nayroles,B.;Touzot,G.;Villon,P.(1992):Generalizing the finite element method.Comput.Mech.,vol.10,pp.307-318.

Ohs,R.R.;Aluru,N.R.(2001):Meshless analysis of piezoelectric devices.Comput.Mech.,vol.27,pp.23-36.

Organ,D.;Fleming,M.;Terry,T.;Belytschko,T.(1996):Continuous meshless approximations for convex bodies by diffraction and transparency.Comput.Mech.,vol.18,pp.1-11.

Pak,Y.E.(1990):Crack extension force in a piezoelectric material.ASME J.Applied Mechanics,vol.57,pp.647-653.

Pak,Y.E.(1992):Linear electro-elastic fracture mechanics of piezoelectric materials.Int.J.Fracture,vol.54,pp.79-100.

Sladek,J.;Sladek,V.;Atluri,S.N.(2004):Meshless local Petrov-Galerkin method in anisotropic elasticity.CMES:Computer Modeling in Engn&Sciences,vol.6,no.5,pp.477-489.

Sladek,J.;Sladek,V.;Wunsche,M.;Zhang,Ch.(2012):Analysis of an interface crack between two dissimilar piezoelectric solids.Eng.Fracture Mech.,vol.89,pp.114–127.

Sladek,J.;Sladek,V.;Zhang,Ch.;Wunsche,M.(2010):Crack analysis in piezoelectric solids with energetically consistent boundary conditions by the MLPG.CMES-Computer Modeling in Engineering&Sciences,vol.68,no.2,pp.185-220.

Sladek,J.;Sladek,V.;Zhang,Ch.;Solek,P.;Pan,E.(2007):Evaluation of fracture parameters in continuously nonhomogeneous piezoelectric solids.Int.J.Fracture,vol.145,pp.313–326.

Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the MLPG method in engineering&Sciences:A review.CMES-Computer Modeling in Engineering&Sciences,vol.92,no.5,pp.423-475.

Sosa,H.(1991):Plane problems in piezoelectric media with defects.Int.J.Solids Structures,vol.28,pp.491-505.

Suresh,S.;Mortensen,A.(1998):Fundamentals of Functionally Graded Materials,Institute of Materials,London.

Ueda,S.(2003):Crack in functionally graded piezoelectric strip bonded to elastic surface layers under electromechanical loading.Theoretical Applied Fracture Mechanics,vol.40,pp.225-236.

Yang,J.(2005):An anti-plane crack in a piezoelectric semiconductor.Int.J.Fracture,vol.136,pp.L27-L32.

Yang,J.S.;Zhou,H.G.(2005):Amplification of acoustic waves in piezoelectric semiconductor plates.Int.J.Solids Structures,vol.42,pp.3171-3183.

Wang,B.L.;Noda,N.(2001):Thermally induced fracture of a smart functionally graded composite structure.Theoretical Applied Fracture Mechanics,vol.35,pp.93-109.

White,D.L.(1962):Amplification of ultrasonic waves in piezoelectric semiconductors.J.Appl.Phys.,vol.33,pp.2547-2554.

Zhu,T.;Zhang,J.D.;Atluri,S.N.(1998):A local boundary integral equation(LBIE)method in computational mechanics,and a meshless discretization approaches.Comput.Mech.,vol.21,pp.223-235.

Zhu,X.;Wang,Z.;Meng,A.(1995):A functionally gradient piezoelectric actuator prepared by metallurgical process in PMN-PZ-PT system.J.Mater.Sci.Lett.,vol.14,pp.516-518.

Zhu,X.;Zhu,J.;Zhou,S.;Li,Q.;Liu,Z.(1999):Microstructures of the monomorph piezoelectric ceramic actuators with functionally gradient.Sensors Actuators A,vol.74,pp.198-202.