Stable higher derivative models withconstraints by Hamiltonian analysis

ZHAI Xianghua, AO Xichen

(Shanghai United Center for Astrophysics (SUCA), Shanghai Normal University, Shanghai 200234, China)

1 Introduction

Recently,Chen et al.[1]proved that the Ostrogradski instability can be removed by the addition of constraints if the original theory′s phase space is reduced.Based on their study,we find the sufficient and necessary condition to establish a stable higher derivative models with constraints,which would help us to find a reasonable field theory with higher derivatives.There has been a reviviscence of interest in higher derivative theories,especially within attempts to modify Einstein′s gravity theory[2-3].Modified gravity theories can predict observed cosmic phenomena without the need for dark energy[4-5]and maybe even dark matter[6-7].The string and brane theories both show that the higher derivative terms could have interesting cosmological implications in high energy realm[8].The higher derviative terms may be interpreted as the quantum corrections of the matter fields[9].The flat spacetime Galileon is a scalar field theory whose Lagrangian involves the higher derivative terms[10].It seems that we should study higher derivative theory if we try to explain some current riddles of physics with deviation from Einstein′s general relativity.However,Ostrogradski[11]proved in the middle of the 19th century that there exists a linear instability in any nondegenerate theory whose fundamental dynamical variable is higher than 2nd order in time derivative.In various modified gravity models,the higher order gravity theories employing terms such asRμνRμν,RμνρδRμνρδorCμνρδCμνρδgenerally suffer the sickness of Ostrogradski instability.It is often possible to accommodate higher derivatives in the Lagrangian while retaining 2nd order field equations.The usual practices are that the original Lagrangian is added by a judicious term including first or higher derivatives,which is basic ingredient for the modified gravity.So far,one does not know if there is a universal Dirac′s method[12]of Hamiltonian analysis to curve Ostragradski′s instability by the addition of constraints.

(1)

and the canonical phase space should have 2N coordinates.Following Ostrogradski′s choices,the canonical coordinates are

Qi≡q(i-1),

(2)

Nondegeneracy means that there exists a functiona(Q1, …,QN,PN),which can be expressed in terms of canonical coordinates by Eq.(3)

(3)

And the Hamiltonian is

(4)

It is easy to find that the Hamiltonian is linear inP1,…,PN-1,so it is not bounded from below (or above).It will become problematic when the interactions with other degrees of freedom are introduced,whose Hamiltonians are bounded from below (or above)[5].

Imposing constraints is a desirable way out to cure Ostrogradski instability for higher derivative theories[1],which makes the Hamiltonian bounded.In other words,the Ostrogradski instability can be removed by the addition of constraints,which reduce the dimensionality of the phase space of original system.One can introduce auxiliary variables to realize the reduction.In fact, the total phase space is enlarged after introducing auxiliary variables,but the dimensionality of the reduced phase space keeps the same or even gets smaller,because trajectories are constrained.It has been proven that the addition of Lagrange multipliers can not reduce the original phase space,so the constraints must contain second or higher derivative terms of auxiliary variables.

The Pais-Uhlenbeck (PU) oscillator[13]is a fascinating toy model for the investigation of higher derivative theories[14-18].It is a quantum mechanical analog to a field theory containing both the second and the fourth order derivative terms.On the classical level, the simplest interaction is an external dissipative force for a PU oscillator[15].On the quantum level,Bender and Mannheim showed that PT-symmetric Hamiltonians are ghost-free up to fourth order[16].A stable and unitary quantum system of the PU oscillator is discussed in Refs.[14].

In this paper,we find the sufficient and necessary condition to establish a stable linear system with constraints,in which the Lagrangian involved with 2nd time derivatives.We also move on and generalize the discussions of linear system to a second time derivative system with arbitrary potentialV(q).We present a class of exactly solvable higher derivative models with and without constraints.We show explicitly that the Ostrogradski instability can be removed by imposing constraints in this model.In the case without constraints,the exact solution of classical dynamics includes four quasi-normal modes (QNMs),among which two modes increase exponentially.That indicates an exponential instability of the system.While in the case with constraints,the two divergent modes are eliminated and the good ones are retained.So the exact solution includes only two stable QNMs.All these discussions and conclusions would pave the way to establish a reasonable field theory with higher order derivative.

This paper is organized as follows.In section 2 we investigate the PU oscillator with an external dissipative force to illustrate the instability of a higher derivative system.In section 3,using Dirac′s Hamlitonian method,we obtain the sufficient and necessary condition to establish a stable linear system with constraints,in which the Lagrangina invloved with 2nd time derivative.We also discuss the generalized system with an arbitray potential term.In section 4,we reexamine the PU model with constraints suggested by Chen et al.[1],and find that model is still not stable within some range of the parametersω1andω2,although it exorcises Ostrogradski instability.In section 5,using the sufficient and necessary condition obtained in Sec.3,we find a stable PU model with constraints for allω1andω2.And this model maintains the characteristics of the PU oscillator.In the last section,we summarize all the investigations,and discuss what we can learn from them.

2 A Pais-Uhlenbeck oscillator with an external dissipative interaction

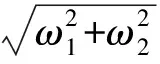
(5)

whereω1andω2are positive constants,and the Euler-Lagrange equation is

(6)

The general solution of Eq.(6) has the format,

q(t)=a1e-iΩ1t+a2e-iΩ2t+a3e-iΩ3t+a4e-iΩ4t,

(7)

whereai(i=1,…,4) are integral constants,and

(8)

(9)

(10)

(11)

and

(12)

(13)

According to Eq.(2),the canonical coordinates are

(14)

The Hamiltonian is obtained by Legendre transforming

(15)

whose linear dependence onP1means the unstableness of the system,which is consistent with the result of the discussion of QNMs for solutions(7).

3 Higher derivative linear system with constraints and its generalization

The Lagrangian contains the whole information about the system dynamics for the fundamental physics,in which possible constraints of dynamical variables can be included.The existence of constraints means that the total phase space is reduced to a submanifold in physics.In order to amend the Ostrogradski instability,the dimensionality of original system′s phase space must be reduced by imposing constraints.Constraints can be classified into two classes.The first class constraints are those associated with gauge freedoms in the theory,and the second class constraints are physical,which means the solutions of motion equations are different with or without constraints.In this paper,we can check all the constraints are connected with second class.

(16)

Therefore,the general second time derivative Lagrangian is given by

(17)

Furthermore,the most general Lagrangian of second time derivative linear system with constraints can be written as

(18)

whereα,β,a,b,candeare real parameters.Following Dirac′s analysis of constraints systems[18]and Ostrogradski′s choice[17],we define canonical variables as

(19)

(20)

(21)

(22)

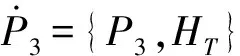
Φ2:{Φ1,HT}=bQ1+cQ2+eP2+(2a-e2)Q3～ 0.

(23)

If the parameters 2a≠e2,Φ1andΦ2are both second class constraints andQ3andP3are functions of other canonical variables,

Q3～(2a-e2)-1(bQ1+cQ2+eP2),P3=0.

(24)

That is to say,further consistency relations only give rise to the form of the arbitrary functionu1,and there′s no further constraints.The source of Ostrogradski instability is the vexatious linear termP1Q2.To exorcise this instability we have to find a constraint whereQ2is some function ofP1.Therefore,we have

2a=e2

(25)

between the parametersaande,if we want to exorcise Ostrogradski instability.

In the 2a=e2case,repeating the procedures above,one can find the further consistency relations

Φ3: {Φ2,HT}=(b+2αe)Q2-eP1+cP2～0,

(26)

Φ4: {Φ3,HT}=(c2-2αe2-2be)Q3-2eβQ1+

2αcQ2-cP1+(b+2αe)P2～0.

(27)

It is easy to check all the constraints are second class constraints.By using these constraints,the reduced Hamiltonian can be written as

(28)

Obviously,the effective dimensionality of phase space is reduced from four (Q1,Q2,P1,P2) to two (Q1,P1),and the Ostrogradski instability is exorcised.Furthermore,the reduced Hamiltonian will be positive or negative definite when suitable relations are satisfied among the parametersα,β,b,cande.

From the discussions above,we obtain Theorem 1 stated as follows,

Theorem1 The most general Lagrangian (18) of second time derivative linear system with constraints is stable and nontrivial iff 2a=e2,e≠0 and

(29)

Also,we can move on and generalize the discussions of the system Eq.(18) to a second time derivative system with arbitrary potentials,whose Lagrangian is as follows,

(30)

(31)

The relationship betweenQ2andP1is

(32)

andQ2can be inverted as a function ofQ1andP1for a fixedc(Q1,Q2) in Eq.(31).So,the dimensionality of phase space can be reduced to two (Q1,P1) from four (Q1,P1,Q2,P2).From Eq.(31) and (32),we obtain Theorem 2,stated as follows,

Theorem2 For a second time derivative dynamical system with constraints,Eq.(30),

(i) By choosing some appropriate functionc(Q1,Q2),one can always change the original system into a stable one,and the dimensionality of the phase space is reduced to two (Q1,P1) from four (Q1,P1,Q2,P2) ,but the characteristics of the constrained system might change essentially.

4 A PU model with constraints: the stability is dependent on parameters ω1 and ω2

We reexamine a PU model with constraints discussed by Chen et al.in Ref.[1],whose Lagrangian is

(33)

Here,we point out that the model is not stable within some range of the parametersω1andω2,although it can exorcise Ostrogradski′s ghost from the system of the PU oscillator.Furthermore,we show the exact solution after introducing an external dissipative force.The canonical variables are defined by

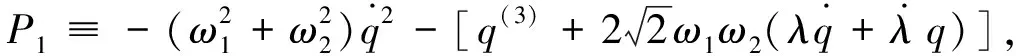
(34)

(35)

Q3≡λ?P3≡0,

(36)

and the total Hamiltonian is

(37)

whereΦ1is primary constraint andΦ1:P3=0.The secondary constraints are

(38)

(39)

(40)

Using these constraints,we obtain the correct expression of the reduced Hamiltonian,

(41)

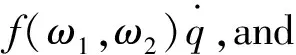
(42)

whereθ(x) is the Heaviside function guaranteeing the positivity of the friction coefficient for allω1,ω2>0.From the Lagrangian (33) and (42),the equations of motion are

(43)

and

(44)

From Eqs.(33) and (42),Eqs.(43) and (44) are reduced to

(45)

and

(46)

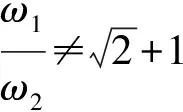
q(t)=μ1e?Ω1 t+μ2e?Ω2t,

(47)

and

(48)

(49)

(50)

(51)

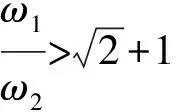
5 A PU model with constraints:the stability is independent on parameters ω1 and ω2

According to the sufficient and necessary condition in Theorem 1,we consider the Lagrangian

(52)

where the choice of parameters satisfies Eq.(29),so this system with constraints is bound to a stable one.The canonical variables are defined by

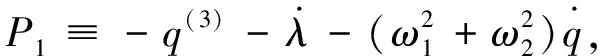
(53)

(54)

Q3≡λ?P3≡0,

(55)

and the total Hamiltonian is

(56)

The primary constraintsΦ1and secondary constraintsΦ2,Φ3andΦ4are

Φ1:P3=0,

(57)

(58)

(59)

(60)

By using the constraints (57)-(60),the reduced Hamiltonian can be written as

(61)

which is negative definite for all values ofω1>0 andω2>0 (See Fig.1).The reduced system is not only free from Ostrogradski′s ghost,but also stable.

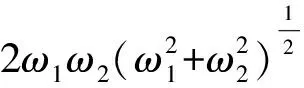
(62)

and

(63)

By some explicit and lengthy calculation,we find the general solutions of Eqs.(62) and (63) are

(64)

and

(65)

whereAandδare integral constants,and

(66)

and

(67)

Here,

(68)

and

(69)

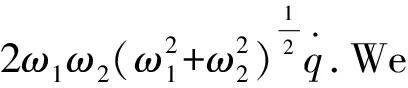
6 Conclusion and discussion

As is known to all,there exists linear instabilities (Ostrogradski instability) in any nondegenerate theory whose fundamental dynamical variable is higher than 2nd order in time derivative.But these instabilities can be removed by imposing constraints which reduce the dimensionality of original system′s phase space.In this paper,we have investigated the most general system of second time derivative linear system with constraints,and showed the sufficient and necessary condition in Theorem 1.Furthermore,we also generalized the investigations of linear system to a higher derivative system with an arbitrary potential termV(q).

Lesson 1: In order to obtain a stable system,we have to choose the Lagrangian of the auxiliary field seriously.In the restricted case of the linear system,Theorem 1 gives an explicit answer,but we should explore further for more general cases.Theorem 2 is just a preliminary study of nonlinear cases.

Lesson 2: The solutions of motion equations are different between the two models with and without second class constraints.One significant reason for the revival of interest in higher derivative theories is related to modified gravity.A reasonable modified gravity model with nondegenerate higher derivatives ought to be free from Ostrogradski instability brought by the higher derivatives,maintain the virtue of the general relativity,and also be competitive in solving the problems such as the accelerating expansion of the universe.When we study modified gravity with nondegnerate higher derivatives,the models are sure to meet these requirements.

Lesson 3: The consistency relation,which introduces a complete set of reasonable constraints,is the key point to remove the factor causing instability of the system.For example,in a linear case,good constraints could eliminate the divergent QNMs,but retain the stable ones.

Finally,for general nonlinear higher derivative theories with constraints,we have found a class of system with the following Lagrangian

(70)

which is free from Ostrogradski′s ghost.We will investigate the stability conditions of this system in the forthcoming work.In any case,the higher derivative theory mentioned above is only a class of toy models for the fundamental physics.It seems that we have to go beyond simple models,if we attempt to explain some current riddles of physics with a deviation from general relativity.However,our experience from the higher derivative theory discussed above would help us to find a reasonable field theory with higher derivatives.

:

[1] CHEN T J,FASIELLO M,LIM E A,et al.Higher derivative theories with constraints:Exorcising Ostrogradski′s Ghost[J].J Cosmol Astropart Phys,2013(2):042,1-17.

[2] SOTIRIOU T P,FARAONI V.f(R) theory of gravity[J].Rev Mod Phys,2010,82:451-497.

[3] CLIFTON T,FERREIRA P G,PADILLA A,SKORDIS C.Modified gravity and cosmology[J].Phys Rept,2012,513:1-189.

[4] BERTONE G,HOOPER D,SILK J.Particle dark matter:evidence,candidates and constraints[J].Phys Rept,2005,405:279-390.

[5] WOODARD R P.Avoiding dark energy with 1/Rmodifications of gravity[C]//PAPANTONOPOULOS L.The Insisible Universe:Dark Matter and Darak Energy,Lect Notes in Phys,Vol 720,Berlin Heidelberg:Springer,2007.

[6] ZHANG H S,LI X Z.MOND cosmology from entropic force[J].Phys Lett B,2012,715:15-18.

[7] CHARMOUSIS C,Goutéraux B,Kiritsis E.Higher-derivative scalar-vector-tensor theories:black holes,Galileons,singularity cloaking and holography[J].J High Energy Phys,2012(9):011,1-44.

[8] ZHANG H S,GUO Z K,CHEN C Y,et al.On asymmetric brane creation[J].J High Energy Phys,2012(1):019,1-19.

[9] CHAPLINE G F,MANTON N S.Unification of Yang-Mills theory and supergravity in ten dimensions[J].Phys Lett B,1983,120:105-109.

[10] NICOLIS A,RATTAZZI R,TRINCHERINI E.Galileon as a local modification of gravity[J].Phys Rev D,2009,79:064036.

[11] OSTROGRADSKI M.Mémoires sur les équations différentielles relatives au problème des isopérimètres[J].Mem Acad St Peterbourg,1850,VI:385-517.

[12] DIRAC P A M.Lectures on Quantum Mechanics[M].New York:Yeshiva University,1964.

[13] PAIS A,UHLENBECK G E.On field theories with non-localized action[J].Phys Rev,1950,79:145-165.

[14] SMILGA A.Ghost-free higher-derivative theory[J].Phys Lett B,2006,632:433-438.

[15] NESTERENKO V V.Instability of classical dynamics in theories with higher derivatives[J].Phys Rev D,2007,75:087703.

[16] BENDER C M,MANNHEIM P D.No-Ghost theorem for the Fourth-Order derivative Pais-Uhlenbeck oscillator model[J].Phys Rev Lett,2008,100:110402.

[17] SMILGA A.Comments on the dynamics of the Pais-Uhlenbeck oscillator[J].SIGMA,2009,5:1-13,17.

[18] ILHAN I B,KOVNER A.Some comments on ghosts and unitarity:The Pais-Uhlenbeck oscillator revisited[J].Phys Rev D,2013,88:044045.