A Class of Regular Simple ω2-semigroups-II

SHANG YU,WANG LI-MINAND FENG YING-YING

(1.Department of Mathematics,Simao Teacher's College,Puer,Yunnan,665000) (2.School of Mathematics,South China Normal University,Guangzhou,510631) (3.Department of Information Science and Mathematics,Foshan University,Foshan, Guangdong,528000)

Communicated by Du Xian-kun

A Class of Regular Simple ω2-semigroups-II

SHANG YU1,WANG LI-MIN2AND FENG YING-YING3

(1.Department of Mathematics,Simao Teacher's College,Puer,Yunnan,665000) (2.School of Mathematics,South China Normal University,Guangzhou,510631) (3.Department of Information Science and Mathematics,Foshan University,Foshan, Guangdong,528000)

Communicated by Du Xian-kun

In this paper,we study regular simple ω2-semigroups in which D|ES=Wdby the generalized Bruck-Reilly extension and obtain its structure theorem.

regular semigroup,simple ω2-semigroup,generalized Bruck-Reilly extension

1 Introduction

For any semigroup S we denote by ESthe set of idempotents of S.Let S be a semigroup whose set ESis non-empty.We define a partial order“≥”on ESsuch that e≥f if and onlyifef=f=fe.Denote by N the set of all non-negative integers and by N+the set of all positive integers.If ES={ei:i∈N}and the elements of ESform a chain e0＞e1＞e2＞···,then S is called an ω-semigroup.We denote by Cωthe set {e0,e1,e2,···}with e0＞e1＞e2＞···We partially order N×N in the following manner: for(m,n),(p,q)∈N×N,

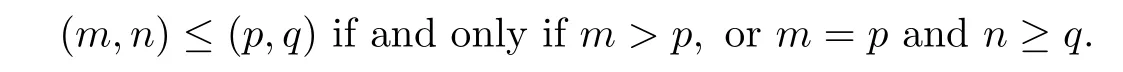
The set N×N with the partial order is called an ω2-chain,and is denoted by C2ω.Any partially ordered set order isomorphic to C2ωis also called an ω2-chain.We say that a semigroup S is an ω2-semigroup if ESis order isomorphic to C2ω.Thus,if S is an ω2-semigroup,then we can write

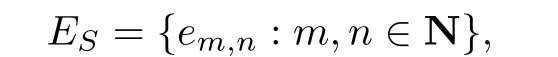
where em,n≤ep,qif and only if(m,n)≤(p,q).In[1],the structure of a bisimple ωsemigroup is shown to be determined entirely by its group of units and an endomorphism of its group of units.Munn[2]studied and classified regular ω-semigroups which are entirely determined by a sequence of groups Gi(i=0,1,···,d-1),homomorphism γd-1of the form Gd-1→G0and homomorphism γiof the form Gi→Gi+1(i=0,···,d-2)if d＞1,where the integer d is characterized as the number of distinct D-classes in this kind of semigroups.Warne[3]investigated the bisimple ωn-semigroups,and proved that any bisimple ωn-semigroup has a structure as(G×Cn,?),where G is a group and Cnis a 2n-cyclic semigroup,under a suitable multiplication.

Regular simple ω2-semigroups can be regarded as a natural generalization of regular simple ω-semigroups.We manage to do the similar work in[2]in this paper for regular simple ω2-semigroups.Section 2 presents some information and other necessary notations and terminology.In Section 3 we construct a regular simple ω2-semigroup in which D|ES=Wdfrom a sequence of groups Gi(i=0,1,···,d-1),homomorphism β,homomorphism γ and an element u of G0by the generalized Bruck-Reilly extension.The integer d is characterized as the number of distinct D-classes in such semigroups.It is then proved in Section 4 that this construction provides the most general regular simple ω2-semigroup in which D|ES=Wd.

2 Definitions and Preliminaries

We use the terminologies and notations in Howie[4]and Petrich[5].Let a,b be the elements of a semigroup S.Then a and b are said to be L[R]-equivalent if and only if S1a=S1b [aS1=bS1].We write H=L∩R and D=L∨R=L?R=R?L.Then L,R,H and D are equivalence relations on S such that H?L?D and H?R?D.Write D|ES=D∩(ES×ES).A semigroup is called bisimple if it contains only one D-class.A semigroup without zero is called simple if it has no proper ideals.A semigroup is simple if and only if for a,b in S there exist x,y in S such that xay=b.We denote by La[Ra,Ha,Da] the L[R,H,D]-class of S containing the element a.For an ω2-semigroup S with ES={em,n: m,n∈N},let Rm,nbe the R-class containing an idempotent em,n,and Lp,qbe the L-class with idempotent ep,q,that is,

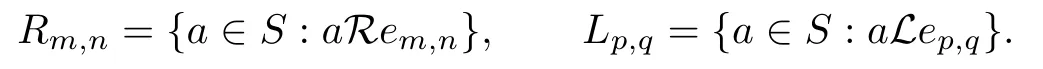
Let H(m,n),(q,p)be the Rm,n∩Lp,q,that is,

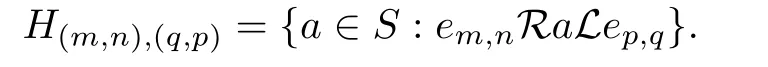
Wang and Shang[6]have shown that the set S=N×N×N×N with the operation defined by

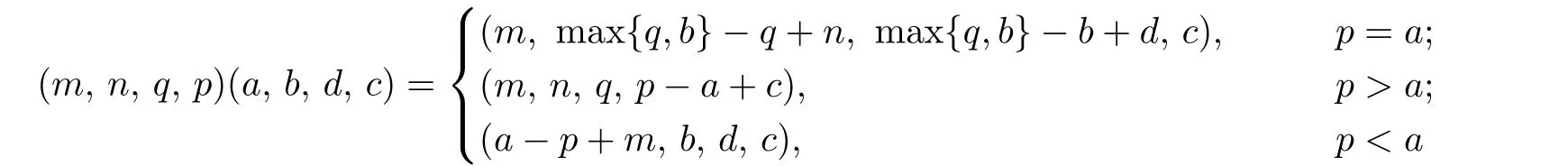
is a bisimple ω2-semigroup and called it the quadrucyclic semigroup,which is denoted by Bω2.Wang and Shang[6]have introduced the generalized Bruck-Reilly extension also.Let

T be a monoid with Heas the H-class which contains the identity element e of T.The set S=N×N×T×N×N is a semigroup with the operation defined by

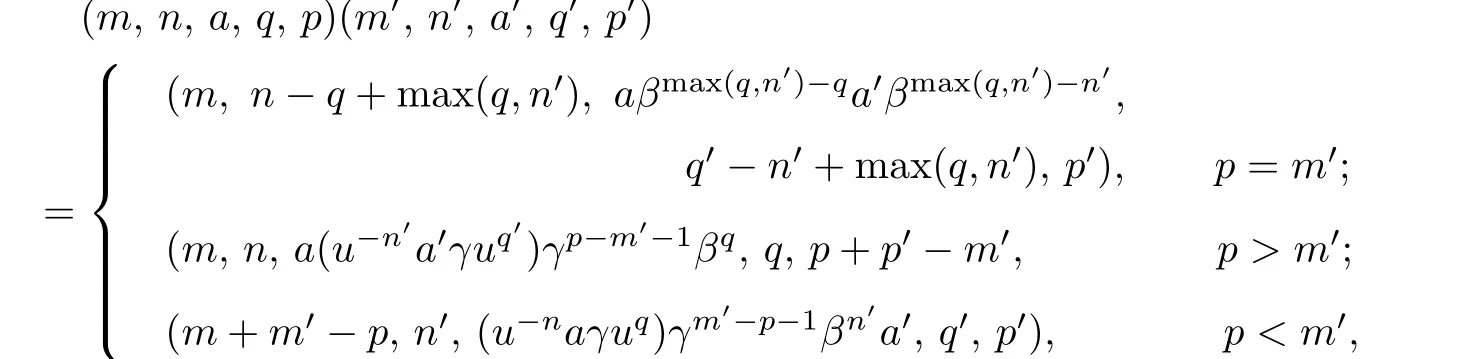
where u is an element of He,τuis the inner automorphism of Hedefined by g→ugu-1,β and γ are two homomorphisms from T into Hesuch that

β0and γ0are interpreted as identity maps of T,and u0=e.The semigroup S=N×N×T× N×N constructed above is called the generalized Bruck-Reilly extension of T determined by β,γ,u,and denoted by GBR(T;β,γ;u).It can be verified that(m,n,a,q,p)is an idempotent of S if and only if m=p,n=q and a2=a.Furthermore,(m,n,a,q,p)is regular if and only if a is regular.An element(m,n,a,q,p)in S has an inverse(i,j,b,l,k)∈S if and only if b is the inverse of a in T,and i=p,j=q,l=n,k=m.For any (m,n,a,q,p),(m′,n′,a′,q′,p′)∈GBR(T;β,γ;u),it can be verified that

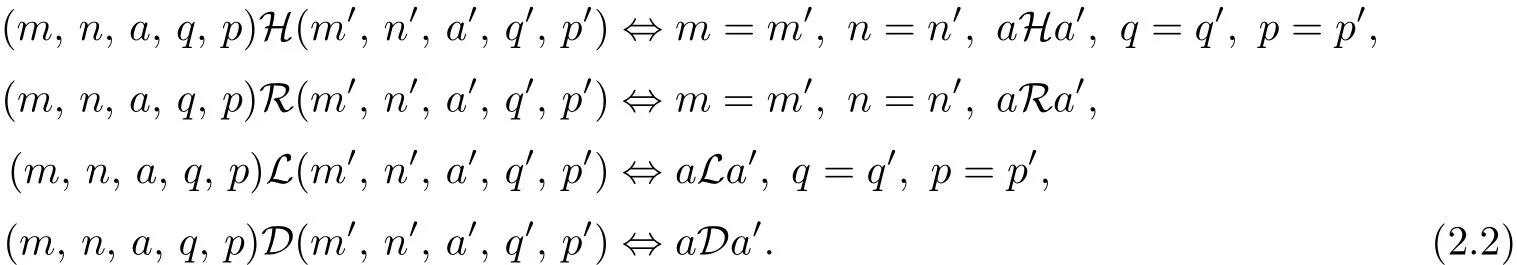
Suppose that we have a semilattice Y and a set of groups Gαindexed by Y,and for all α≥β in Y there exists a homomorphism φα,β:Gα→Gβsuch that

(i)for all α in Y φα,α=1Gα;

(ii)for all α,β,γ in Y such that α≥β≥γ,φα,βφβ,γ=φα,γ. Now define a multiplication inby the rule that,for each x in Gαand y in Gβ,

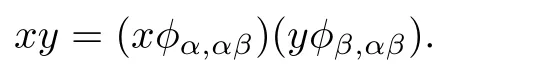
Then S is a semigroup,called a strong semilattice of groups.We write S=S(Y;Gα;φα,β). From[4],we know that S is a Cliffordsemigroup if and only if S is a strong semilattice of groups.We also know that S is a Clifford semigroup if and only if S is regular and every D-class contains exactly one idempotent.

Let E be a semilattice.For each e in E the set Ee={i∈E:i≤e}is a principal ideal of E.The uniformity relation U on E is given by U={(e,f)∈E×E:Ee?Ef}. For each(e,f)in U,we define Te,fto be the set of all isomorphisms from Ee onto Ef.LetThen TEis called the Munn semigroup of the semilattice E.From[4], we know that TEis an inverse semigroup and ETE?E.A semilattice E is rigid if there is only one isomorphism between Ee and Ef for each pair e,f∈E.

Lemma 2.1([4],Theorem 5.4.4)For every inverse semigroup S with semilattice of idempotents E there is a homomorphism φ:S→TEwhose kernel isμ,the maximum idempotent separating congruences on S.

Lemma 2.2[4]Let S be an inverse semigroup with semilattice of idempotents E and E be rigid.Then the semigroup S has the property thatμ=H,and H is a congruence.

Let M={(x,y,p,q,m,n)∈N×N×N×N×N×N:(x,y)≤(p,q)}.We define a map α:M→N by the rule that

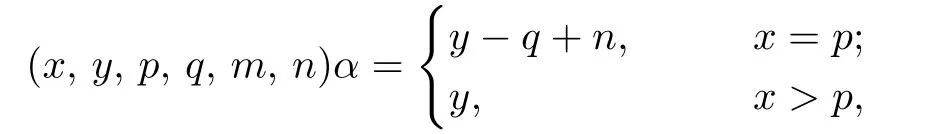
and a binary operation“*”on N×N such that(p,q)*(m,n)=min{(p,q),(m,n)}.Let E=Cω2={em,n:m,n∈N}be an ω2-chain with

Then Eem,n={ei,j:(i,j)≤(m,n)},and Eem,n?Eep,qfor every m,n,p,q∈N.The only isomorphism from Eem,nonto Eep,qis δ(m,n),(p,q),given by

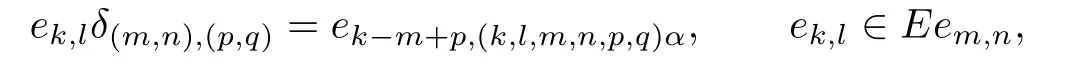
the inverse being

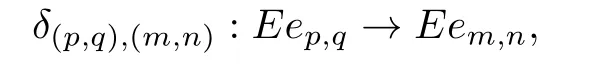
def i ned by

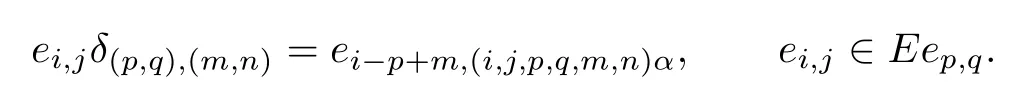
Thus,Cω2is rigid.Ifandare the elements of TE,then their product mapsonto.If we write(x,y)= (p,q)*(a,b),then we can say thamapsonto Eex-a+c,(x,y,a,b,c,d)α.Hence

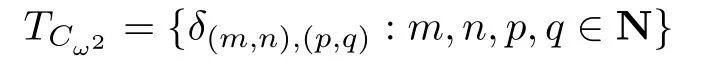
with the operation defined by

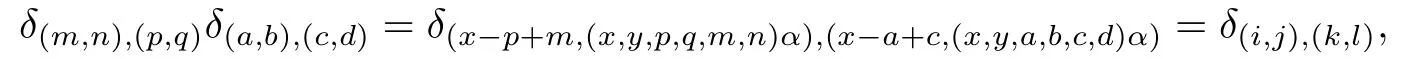
where(x,y)=(p,q)*(a,b)and

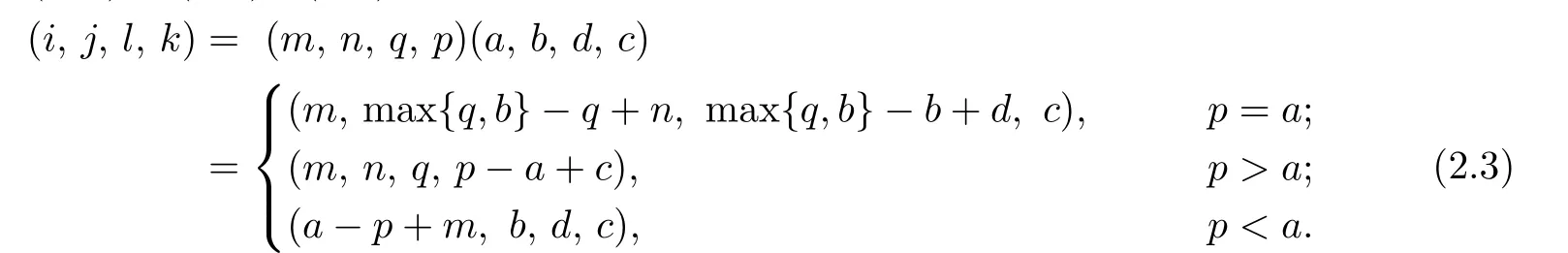
Let S be a regular ω2-semigroup with ES={em,n:m,n∈N}.Then S is an inverse semigroup and TESis isomorphic to TCω2.By Lemma 2.1,there is a homomorphism φ: S→TCω2whose kernel isμ.In fact,by Lemma 2.2,μ=H.A typical H-class of S is

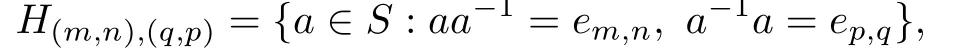
and by the proof of Lemma 2.1,each element a of H(m,n),(q,p)is maped by φ to an element αaof TCω2whose domain is Eaa-1=Eem,nand image is Ea-1a=Eep,q.There is only one such element,and so

Hence we have established the following Lemma.

Lemma 2.3Let S be a regular ω2-semigroup.Then

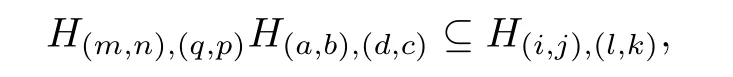
where(i,j,l,k)is the same as(2.3).

Let S be a regular simple ω2-semigroup with the set{em,n:m,n∈N}of idempotents, d be any positive integer,and em,n,ep,q∈ES.The relation Wdis defined on ESby

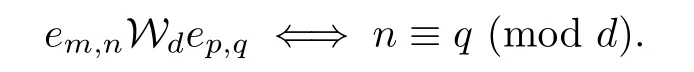
Wdis an equivalence relation on ES.In what follows we study regular simple ω2-semigroup in which D|ES=Wd.We conclude this section with an example of a regular simple ω2-semigroup such that D|ES=Wd.Let d be any positive integer and B0,dbe defined by

where Bω2is the quadrucyclic semigroup.Then B0,dis a subsemigroup of Bω2.Furthermore, it can be shown that B0,dis a regular simple ω2-semigroup in which D|ES=Wd.

3 The Semigroup GBR(T;β,γ;u)

In this section we give a process for constructing a regular simple ω2-semigroup in which D|ES=Wdfrom a finite set of groups and homomorphisms.In particular,the number of D-classes of such semigroup is finite.In Section 4 this construction yields the most general type of regular simple ω2-semigroup in which D|ES=Wd.

We now take T to be a strong semilattice of groups—a Clifford semigroup—of a special form.More precisely,let T be the union of disjoint groups G0,G1,···,Gd-1,where d is a positive integer,and for i=0,1,···,d-2,let γi:Gi→Gi+1be a homomorphism.Then, for all i,j in{0,1,···,d-1}with i＜j,there is a homomorphism αi,j:Gi→Gjdefined by

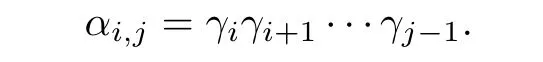
If,for each i in{0,1,···,d-1},we define αi,ito be the identity map of Gi,then we certainly have

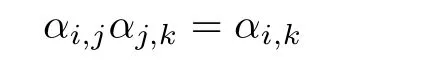
whenever i≤j≤k,and so we have a Clifford semigroup T=S(Y;Gi;αi,j),in which the semilattice Y is the chain{0,1,···,d-1}.We denote the idempotents of T by f0,f1,···, fd-1(the identity elements of G0,G1,···,Gd-1,respectively).Note that in T,

The element f0is the identity of T.We refer to T as a finite chain of groups of length d.

Theorem 3.1Let T be a finite chain of groups of length d.Then GBR(T;β,γ;u)is a regular simple ω2-semigroup with exactly d D-classes such that D|ES=Wd.

Proof.Write S=GBR(T;β,γ;u).Let fibe the identity of the group Gi,and for gi∈Gi,be the inverse of giin Gi(i=0,···,d-1).

We know that S is a semigroup.Let(m,n,gi,q,p)∈S.Since

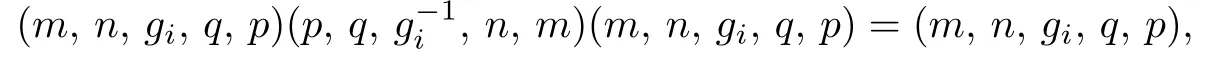
S is regular.The identity of S is(0,0,f0,0,0)and it is readily verified that

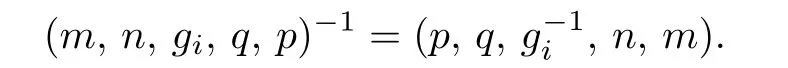
Let(m,n,a,q,p),(m′,n′,a′,q′,p′)∈S.There exist(m′,n′,(aβ)-1,n+1,m)and(p,q+ 1,a′,q′,p′)in S such that

So S is simple.

Next we prove that{(m,n,fi,n,m):m,n∈N;i=0,···,d-1}is the set of idempotents of S.It is clear that(m,n,fi,n,m)is an idempotent.Conversely,let x=(m,n,gi,q,p), where x2=x.Then it follows from(m,n,gi,q,p)(m,n,gi,q,p)=(m,n,gi,q,p)that p＞m or p＜m which is impossible.Thus p=m and so

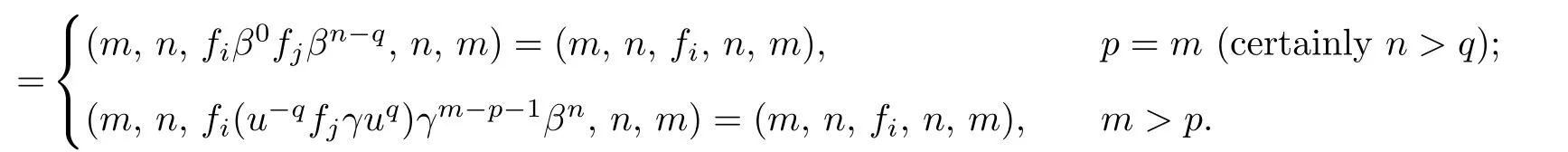
Hence(m,n,fi,n,m)＜(p,q,fj,q,p).It follows that,under the natural partial ordering,the idempotents form a chain

For any m,i,j∈N with 0≤j≤d-1,we write em,n=(m,i,fj,i,m)with n=id+j. Then the set of idempotents of S is:m,n∈N}.Andif and only if(m,n)≤(p,q).Thus S is an ω2-semigroup.For any em,n,ep,q∈ES,by(2.2),we have that (em,n,ep,q)∈D if and only if n≡q(mod d).So S is a regular simple ω2-semigroup in which D|ES=Wd.

Now we show that S has exactly d D-classes.Since S is regular in which each D-class contains an idempotent,it is sufficient to show that

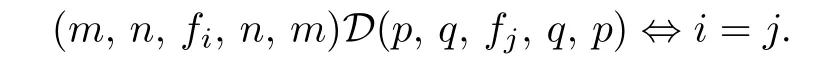
Write e=(m,n,fi,n,m),e′=(p,q,fj,q,p).We use the fact that(e,e′)∈D if and only if there exists x∈S such that xx-1=e,x-1x=e′.

First suppose that(e,e′)∈D.Let x=(u,v,gk,r,s),where xx-1=e,x-1x=e′.Since xx-1=(u,v,fk,v,u)and x-1x=(s,r,fk,r,s),we see,in particular,that i=k=j. Conversely,suppose that i=j.Take x=(m,n,fi,q,p).Then xx-1=e and x-1x=e′, which shows that(e,e′)∈D.This completes the proof of the theorem.

4 The Structure Theorem

This section is devoted to showing that any regular simple ω2-semigroup in which D|ES=Wdis isomorphic to a semigroup of the type GBR(T;β,γ;u).

We follow the notations given in Section 2.Let S be a regular simple ω2-semigroup in which D|ES=Wd.Then we can write ES={em,n:m,n∈N},where em,n≤ep,qif and only if(m,n)≤(p,q).To save repetition,the full hypotheses is not restated for successive lemmas.

Lemma 4.1∈D for all i,j,k,n∈N.

Since every idempotent of S is of the form em,id+jfor some m,i,j∈N such that 0≤j＜d,the result shows that S has at most d distinct D-classes.The next lemma establishes that there are exactly d D-classes.

Lemma 4.2Let i,j∈N and 0≤i＜j＜d.Then)/∈D.

Proof.Notice that D|ES=Wd,and the proof is trivial.

From the previous two lemmas we can now state which of theare non-empty.

Lemma 4.3For any m,n,p,q∈N,the following conditions are equivalent:

(i)H(m,n),(q,p)/=?;

(ii)(em,n,ep,q)∈D;

(iii)n≡q(mod d).

Let the D-class of S containing e0,ibe denoted by Di(i=0,1,···,d-1)and let the groupe denoted by Gi(i=0,1,···,d-1).Evidently,and Di∩Dj=? if 0≤i＜j≤d-1.

Lemma 4.4(i)Diis a bisimple ω2-semigroup with identity e0,iand group of units Gi.

(ii)The R[L]-classes of Diare the sets(k,n∈N).

Proof.(i)Since S is regular and its idempotents form a chain,each Diis a bisimple inverse subsemigroup of S(see[7]).Moreover,by Lemma 4.3,the set of idempotents of Diis{ek,nd+i:k,n∈N}.Thus Diis a bisimple ω2-semigroup with identity e0,i.The group of units of Diis the maximal subgroup of Dicontaining e0,i.But Gi?Diand Giis the maximal subgroup of S containing e0,i.Hence the group of units of Diis Gi.

(ii)From Lemma 4.3 we have that

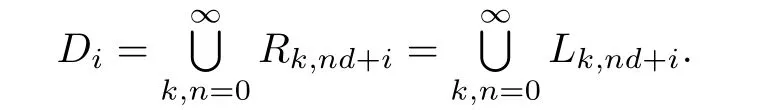
It is clear that each R-class of Diis contained in an R-class of S.Let k,n∈N and.To show thatis an R-class of Diit is enough to prove that a and b are R-equivalent in Di.Since(a,b)∈R there exist elements x,y such that a=bx,b=ay. Write.Then a=bx′,b=ay′.Further,(a,x′)∈L and (b,y′)∈L.Hence x′,y′∈Di.This gives the required result.

Lemma 4.5Let ai∈H(0,i),(d+i,0)and bi∈H(0,i),(i,1)(0≤i＜d).Take a0i=e0,i,.Then

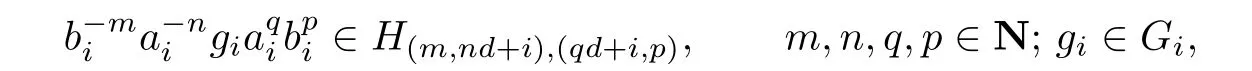
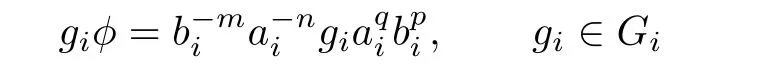
is a bijection.

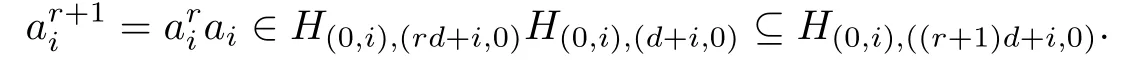
Hence,for all non-negative integers n,Similarly,let m,n be any nonnegative integers.Then

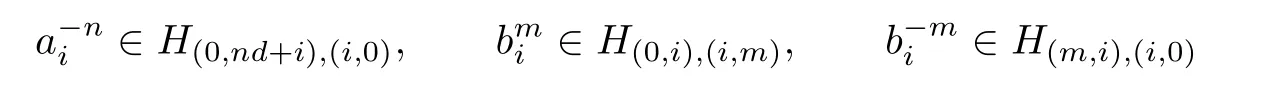
satisfy

Thus,by Lemma 2.3,

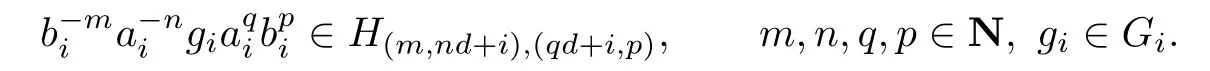
If

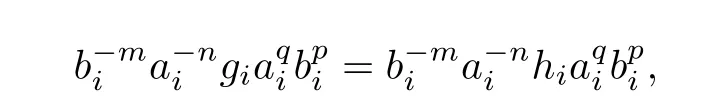
then

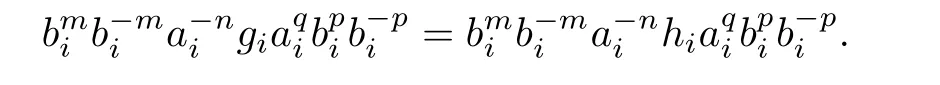
So

Thus

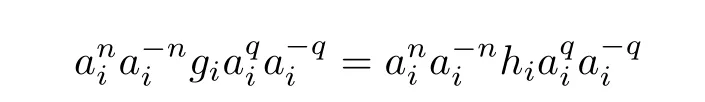
and g=h.Also,with

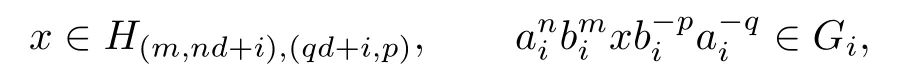
we get

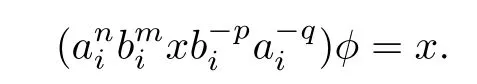
Therefore,φ is a bijection.

Lemma 4.6,0≤i＜d.

Lemma 4.7Every element of S is uniquely expressible in the form

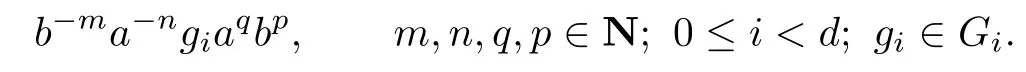
Proof.Let 0≤i＜d.We first show that

This holds trivially for n=1.Assume that(e0,ia)r=e0,iarfor some positive integer r.By Lemma 4.6,e0,ia∈H(0,i),(d+i,0)?Di,and so

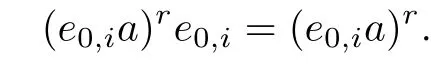
Hence

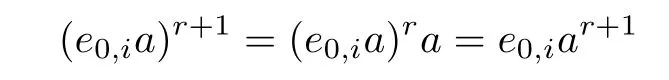
and the result follows.Similarly,,n=1,2,3,···

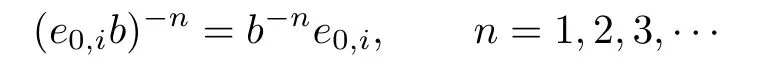
Now take ai=e0,ia and bi=e0,ib in Lemma 4.5.Also(e0,ia)n=e0,ianfor all positive integers n and it holds also for n=0 since a0iand a0are defined to be ei,0and e0,0respectively.Similarly,andN).

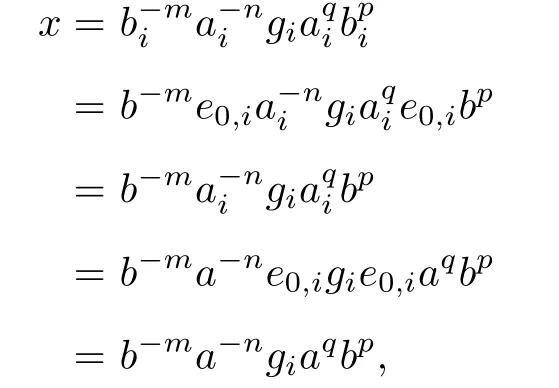
where gi∈Gi.Moreover,if,then

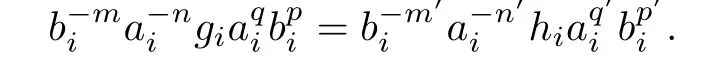
So m=m′,n=n′,q=q′,p=p′and gi=hiby Lemma 4.5.Thus the expression for x is unique.

Lemma 4.8Let 0≤i＜d,gi∈Gi.Thenand

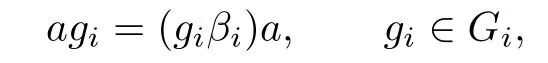
and γi:Gi→G0by the equation

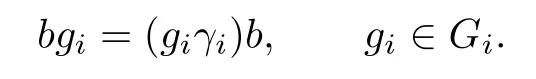
Let

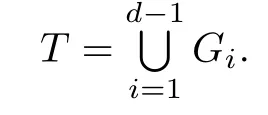
For i,j∈{0,1,···,d-1}with i≤j,by Lemma 2.3 and the fact that

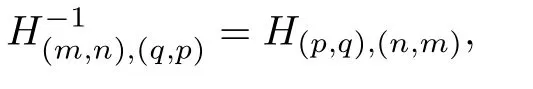
we have

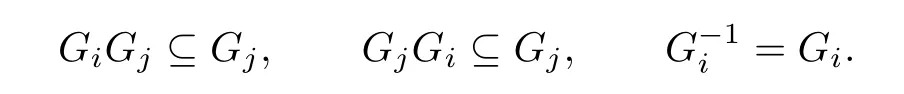
Hence T is an inverse subsemigroup of S.Since it is also evidently completely regular,T is, in fact,a Clifford semigroup in which the idempotents form the finite chain

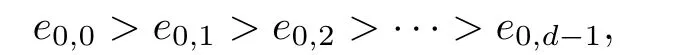
where e0,iis the identity of the group Gi(i=0,1,···,d-1).Thus T is a finite chain of groups of length d.Since the groups G0,G1,···,Gd-1are disjoint,we can use the maps β1,β2,···,βd-1thus obtained to piece together a map β:T→G0,

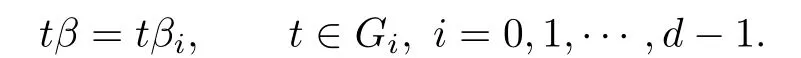
Similarly,we obtain a map γ:T→G0,

Lemma 4.9β and γ are two homomorphisms.

Proof.Let x,y∈T,where x∈Gi,y∈Gjand i≤j.Then

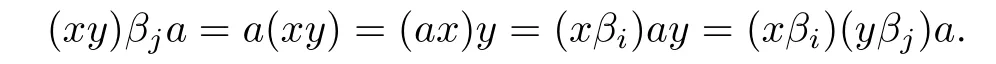
Since aa-1=e0,0,one has

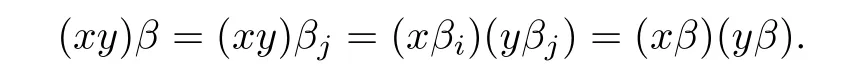
Thus β is a homomorphism.Similarly,γ is a homomorphism.

Lemma 4.10Let x∈T and k be a non-negative integer.Then

(i)akx=(xβk)ak;

(ii)xa-k=a-k(xβk);

(iii)bkx=(xγk)bk;

(iv)xb-k=b-k(xγk).

Proof.(i)The result holds for k=0.Assume that it holds for k=n-1(n＞1).Then

Hence the result holds for r=n.So,by induction,it holds for all non-negative integers k.

(ii)From agi=(giβi)a(gi∈Gi)we can deduce that g-1

ia-1=a-1(giβi)-1for every giin Gi.Hence,changing notion,we deduce that gia-1=a-1(giβi)(gi∈Gi).Similar to (i),we have xa-k=a-k(xβk)for all non-negative integers k.

(iii)Similar to(i).

(iv)Similar to(ii).

Lemma 4.11Let u=bab-1.Thenandfor all n∈N,where a0=e0,0,b0=e0,0and u0=e0,0.

Lemma 4.12Let u=bab-1.Then u∈G0and γτu=βγ.

Proof.We may deduce from H(0,0),(0,1)H(0,0),(d,0)H(1,0),(0,0)?H(0,0),(0,0)that u=bab-1∈G0and

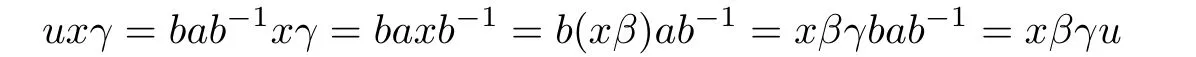
for each x∈T.Therefore,for all x∈T,uxγu-1=xβγ.Hence xγτu=xβγ,where τu:G0→G0is the automorphism defined by yτu=uyu-1.Thus we obtain γτu=βγ.

We now come to the main result.

Theorem 4.1Let S be a regular simple ω2-semigroup in which D|ES=Wd.Then S?GBR(T;β,γ;u)for some T,β,γ,u.

Proof.Let T,β,γ,u be as above.By Lemma 4.7,every element of S is uniquely expressible in the form b-ma-ngaqbp(m,n,p,q∈N;g∈T).

Let x=b-ma-ngaqbp,y=b-m′a-n′g′aq′bp′,where m,n,p,q,m′,n′,p′,q′∈N and g,g′∈T.To simplify the productxy we distinguish three cases.

I.If p=m′,then bp-m′=e0,0.Hence xy=b-ma-ngaq-n′g′aq′bp′.If q=n′,then xy=b-ma-ngg′aq′bp′;If q＞n′,then xy=b-ma-ng(g′βq-n′)aq+q′-n′bp′;If q＜n′,then xy=b-ma-(n-q+n′)(gβn′-q)g′aq′bp′.

II.If p＞m′,then,by Lemmas 4.10 and 4.11,we have

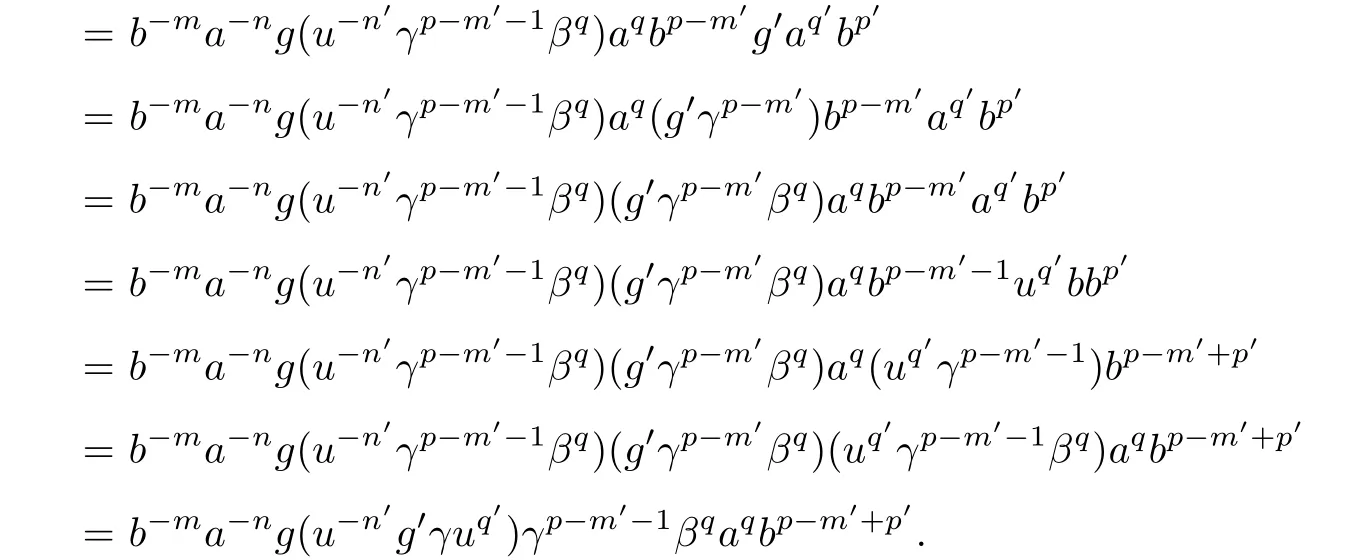
III.If p＜m′,then,by Lemmas 4.10 and 4.11,we have

Thus the mapping ψ:S→GBR(T;β,γ;u)defined by

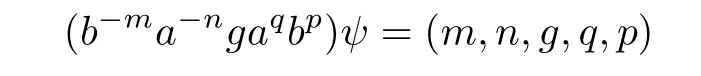
is an isomorphism.This completes the proof.

[1]Reilly N R.Bisimple ω-semigroups.Proc.Glasg.Math.Assoc.,1966,7:160–167.

[2]Munn W D.Regular ω-semigroups.Glasg.Math.J.,1968,9:46–66.

[3]Warne R J.Bisimple inverse semigroups mod groups.Duke Math.J.,1967,34:787–811.

[4]Howie J M.Fundamentals of Semigroup Theory.Oxford:Clarendon Press,1995.

[5]Petrich M.Inverse Semigroups.New York:Wiley-Interscience,1984.

[6]Wang L M,Shang Y.Regular bisimple ω2-semigroups.Adv.Math.(China),2008,37(1):121–122.

[7]Warne R J.A characterization of certain regular d-classes in semigroups.Illinois J.Math.,1965, 9:304–306.

20M10

A

1674-5647(2013)04-0351-12

Received date:July 5,2011.

The NSF(10901134)of China and the Science Foundation(2011Y478)of the Department of Education of Yunnan Province.

E-mail address:shangyu503@163.com(Shang Y).