Structural,Elastic,Electronic and Optical Properties of Zinc-Blende MTe(M=Zn/Mg)

GUO Lei HU Ge,* FENG Wen-Jiang ZHANG Sheng-Tao

(1School of Chemistry and Chemical Engineering,Chongqing University,Chongqing 400044,P.R.China;2College of Physics Science and Technology,Shenyang Normal University,Shenyang 110034,P.R.China)

1 lntroduction

In the last few decades,II-VI ground semiconductors(MX;M=Be,Mg,Ca,Ba,Zn,Cd,Hg,X=O,S,Se,Te)have attracted both scientific and technological interest due to their good chemical and physical properties,technological applications in fabricating light-emitting devices.1The devices are used in rectifiers,transparent conductors,optical switching,solar cells,visible-light detectors,solid-state laser devices,etc.2,3Complex quantum structures such as quantum wires and wells,self organised quantum dots,laser structures,and microcavities are grown using II-VI materials(ZnTe,CdTe,and MgTe).4

In recent years numerical simulations,and increasing computational power of the computer have made it possible to predict properties of solids under experimental conditions with great accuracy.The electronic band structures of ZnTe and BeTe have been investigated by Joshiet al.5using empirical pseudo-potential method.A three-body potential(Tersoff potential)coupled with a molecular-dynamics(MD)method have been used to calculate structural and thermodynamic properties of ZnTe in zinc-blende(B3)phase.6Duanet al.7calculated the electronic band structures of zinc-blende ZnTe and CdTe applying a self-consistent full-potential linearized augmented planewave(FP-LAPW)method.Khenataet al.8have used the local density approximation(LDA)within the FP-LAPW+lo method to study the structural,electronic and optical properties of ZnX(X=S/Se/Te)in B3 structure.Experimental structural studies on MgTe are less frequently reported mainly because of its high hygroscopicity.However,there were a large amount of reports on the studies of structural properties and possible phase transitions under pressure for MgTe9-11and ZnTe3,12,13.For ZnTe the structural sequence under pressure is B3→cinnabar→Cmcm.Cocoletzi's results9show that generalized gradient approximation(GGA)calculations predict the ground state phase:wurtzite/B3 for MgTe.Gko?luet al.14investigated the structural stability of three magnesium chalcogenides using projector augmented waves(PAW)potentials.They found that zincblende and wurtzite structures have similar energetics for MgTe using both LDAandGGAfunctionals.

With the development of functional,DFT15leads to more and more accurate results from the initial LDA,GGAto hybridization functional.Further,different computation methods can result in tiny differences.In this work,we performab initiocalculations for binary compounds MgTe and ZnTe in B3 structure by using a pseudopotential plane wave(PP-PW)method.Our main aim is to present a systematic and complementary investigation on the structural stabilities,elastic,electronic,and optical properties.The lattice parameters,band-gap energies,density of states(DOS),elastic and dielectric constants are theoretically reported.Comparisons have been made wherever possible with the experimental and previously reported theoretical data.

2 Computational methods

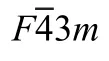
The first-principles calculations were performed within DFT,as implemented in the CASTEP16package.The exchange-correlation function was described in GGA with Perdew-Burke-Ernzerhof parameterization method.17We used the ultrasoft vanderbilt pseudopotential18to describe the electron-ion interaction.The Mg(2p63s2),Te(5s25p4),and Zn(3d104s2)electrons were treated as valence electrons.The plane-wave basis set cut-off was 380 eV for all cases.The special point sampling integration over the Brillouin zone was employed by using the Monkhorst-Pack method with varied specialk-point mesh.19The tolerances for geometry optimization were set as the difference in total energy within 5.0×10-6eV·atom-1,the maximum ionic Hellmann-Feynman force within 0.1 eV·nm-1,the maximum ionic displacement within 5.0×10-5nm,and the maximum stress within 0.02 GPa.

Considering the usual underestimation of energy gaps within the GGA/LDA approximation which is known to result from the discontinuity of the exchange-correlation energy,screened exchange LDA(sX-LDA)20and the hybrid density functional B3LYP21were also applied here to obtain more reliable electronic properties,which are computationally much less demanding than using the GW quasiparticle method.

Elastic constants were calculated for cubic lattice structures.In this work,the volume contribution to total energy can be eliminated using volume conserving strains.For both structures,we carried out calculations for strains in the range of-0.003 to 0.003 with the step of 0.0012 for each distortion.The systems were fully relaxed after each distortion in order to reach the equilibrium state with approximately zero forces on all atoms.22Here,the second-order elastic constants were determined by the analysis of change in calculated stress values resulting from change in the strain.

Optical properties of a solid may be determined using the complex dielectric functionε(ω)=ε1(ω)+iε2(ω),which is mainly connected with the electronic structures.23The imaginary part of the dielectric functionε2(ω)was calculated from the momentum matrix elements between the occupied and unoccupied wave functions24as follows:

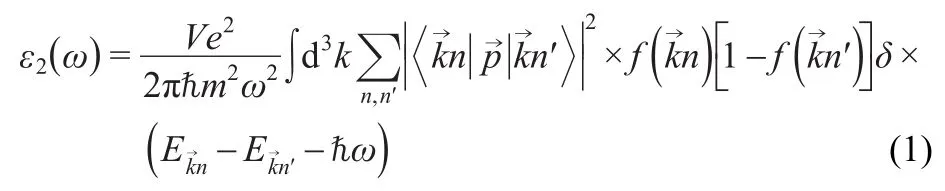
whereeis the electron charge,mis the electron mass,Vis the unit cell volume,ωis the photon frequency,is the momentum operator,ωis the energy of the incident phonon,andare the conduction band(CB)and valence band(VB)wave functions corresponding to thenth andn′th eigenvalue with crystal momentum,andis the Fermi distribution func-tion.The real part of the dielectric functionε1(ω)can be attracted fromε2(ω)by using the Kramers-Kronig relationship:25

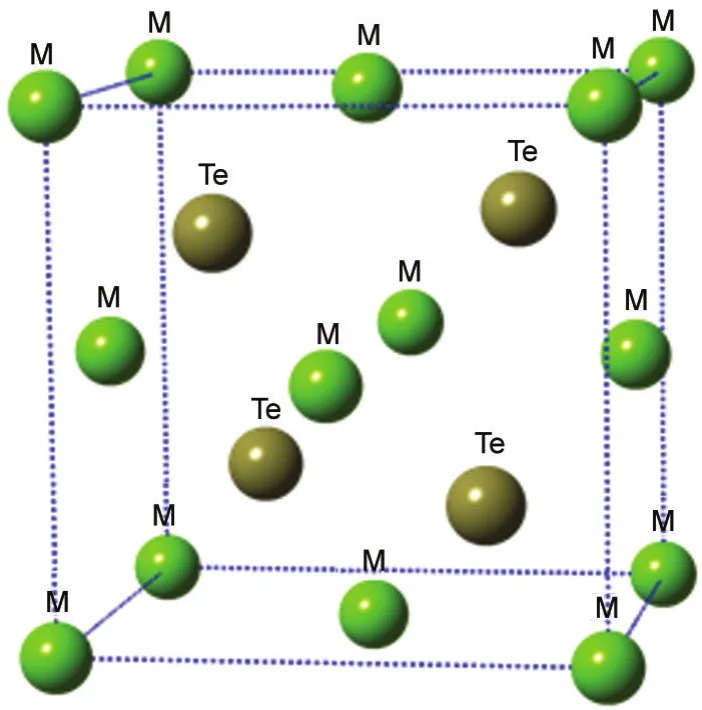
Fig.1 Zinc-blend conventional unit cells of bulk MTe(M=Mg/Zn)

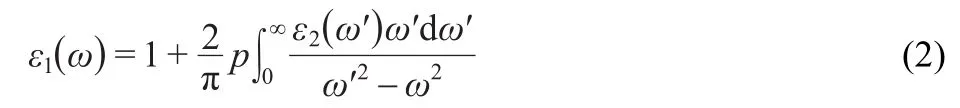
wherepis the principal value of the integral.The knowledge of both the real and imaginary parts of the dielectric function allows the calculation of important optical functions such as the refractive indexn(ω),normal-incidence reflectivityR(ω),and energy-loss spectrumL(ω):

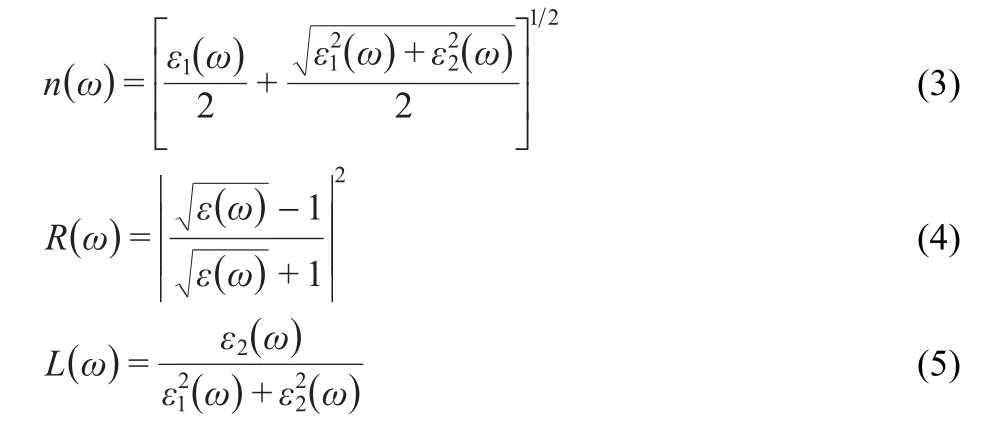
3 Results and discussion

3.1 Structural properties

Firstly,the total energies of MTe(M=Zn/Mg)with a set of volumes were calculated.Then the lattice constantsa0,bulk modulusBand its derivativeB'were obtained by fitting the entire energyversusvolume according to the Birch-Murnaghan equation of states(EOS),26and were summarized in Table 1,together with previous data.3,4,13,14,27,28

The calculated structural parameters are 0.618 and 0.652 nm for ZnTe and MgTe,respectively,it can be clearly seen that they are slightly beyond the experimental values.This overestimation of the lattice constants based on the GGAmethod is reasonable.The small discrepancies compared to other theoretical results may be explained by using different approximations in the density functional methods.In Table 1,the calculated bulk modulus is 49.7 and 34.3 GPa for ZnTe and MgTe,the corresponding compressibility is 0.02 and 0.03,respectively.This result confirms the validity of the empirical relation proposed by Cohen,29B=1761d-3.5(wheredis the nearest-neighbor distance in angstroms).

To investigate the phase stability,the enthalpy of formation(ΔfH)of MTe compounds was calculated by using the following expressions:30

Table 1 Calculated lattice constant(a0),bulk modulus(B),and pressure derivative(B′)at equilibrium volume in B3 structure for MTe(M=Zn/Mg)compounds compared with previous results

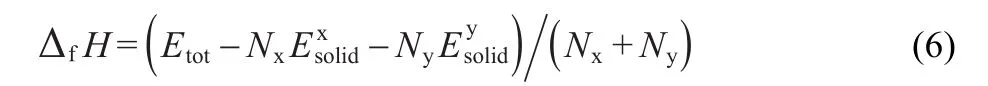
We calculate the ΔfHand obtain the results of-6.65 and-5.81 eV for MgTe and ZnTe,respectively.The fact that all enthalpy of formation are negative means that the structure,of both compounds can exist and should be stable.Generally speaking,larger ΔfHvalue provides lower thermodynamic stability.Grounded on these calculated values,we conclude that MgTe phase is more stable than ZnTe due to the smaller ΔfHin the ground state.

3.2 Elastic properties

The elastic constants are fundamental and indispensable parameters that describe the response to an applied macroscopic stress and especially important as they are related to various physical properties,such as the elasticity,mechanical stability and stiffness of materials.

For cubic crystals,there are three independent elastic constants(C11,C12,andC44)and the traditional mechanical stability conditions areC11-C12＞0,C11＞0,C44＞0,C11+2C12＞0,C12＜B＜C11.For MTe(M=Zn/Mg)compounds,the present elastic constants in Table 2 satisfy these stability criterions,indicating that they are mechanically stable.

The Poisson's ratiov,Zener anisotropy factorA,and Young's modulusE,which are the most interesting elastic properties for applications,are often measured for polycrystalline materials when investigating their hardness.These quantities are calculated in term of the computed data using the following relations:

whereB=(C11+2C12)/3,is bulk modulus,andG=(GR+GV)/2,is the isotropic shear modulus,GRis the Reuss's shear modulus corresponding to the lower bound ofGvalues,andGVis the Voigt's shear modulus corresponding to the upper bound ofGvalues;they can be written as:GV=(C11-C12+3C44)/5,5/GR=4/(C11-C12)+3/C44.

The Kleinman parameterξdescribes the relative positions of the cation and anion sublattices under volume conserving strain distortions for which positions are not fixed by symmetry.It is known that a low value ofξimplies the existence of a large resistance against bond bending or bond-angle distortion andvice versa.31This parameter can be written as:

The calculated elastic constants,B,A,v,E,G,andξ,based on the above expressions,for MTe are found to be in reason-able order and given in Table 2.Also are shown for comparison the available experimental32and theoretical8data from the literature.Contrast Table 1 with Table 2,the bulk modulus from the total energy minimization and elastic constants have nearly the same value.This may be an estimate of the reliability and accuracy of our calculated elastic constants.Form Table 2,it is obvious to observe a light difference between our results and those found recently.It results from the different input data and calculated methods which have been used.We can see that theAvalues are greater than 1.0 and we cannot regard MgTe and ZnTe as elastically isotropic.Push33introduced the ratio of the bulk modulus to shear modulus(B/G)of polycrystalline phases as prediction of the brittleness and ductile behavior of materials.A high(low)B/Gvalue is associated with ductility(brittleness).The critical value which separates ductility from brittleness is about 1.75.It can be seen that both compounds are not brittle materials.According to the Young's modulusE,MgTe has a better plasticity than ZnTe,but the latter is stiffer than the former.νprovides the information about the characteristic of the bonding forces.The calculatedνfor ZnTe is very close to 0.25,which means that this material is with predominantly central inter-atomic forces.34

Table 2 Calculated bulk modulus(B),elastic constants(Cij),shear modulus(G),Young's modulus(E),B/G,Zener anisotropy factor(A),Poisson's ratio(ν),and Kleinman parameter(ξ)for MTe(Te=Zn/Mg)

The Debye temperature(ΘD)is known to be an important fundamental parameter closely related to many physical properties,and is used to distinguish between high-and low-temperature regions for a solid.IfT＞ΘDwe expect all modes to have energykBT,and ifT＜ΘDone expects high-frequency modes to be frozen.35Hence,at low temperatures the Debye temperature calculated from elastic constants is the same as that determined from specific heat measurements.We have estimated theΘDusing the calculated elastic constant data,sinceΘDis proportional to the sound velocity(averaged)νmby the equation36

wherehis Planck's constant,kBis Boltzmann's constant,NAis Avogadro's number,nis the number of atoms per formula unit,Mis the molecular mass per formula unit,ρis the density,andνmis approximately given by

whereνtandνlare the transverse and longitudinal elastic wave velocities,respectively,which are obtained from the Navier's equation37

The present Debye temperatures computed for ZnTe and MgTe are 758 and 585 K,respectively.The Debye temperature defines a division line between quantum mechanical and classical behaviour of phonons.In the absence of any available measured data in the literature,they could not be compared.Future experimental work will testify our calculated results.ΘDcan be used to describe the strength of the covalent bond in solid.Thus,the covalent interaction in ZnTe could be stronger.

3.3 Electronic and bonding properties

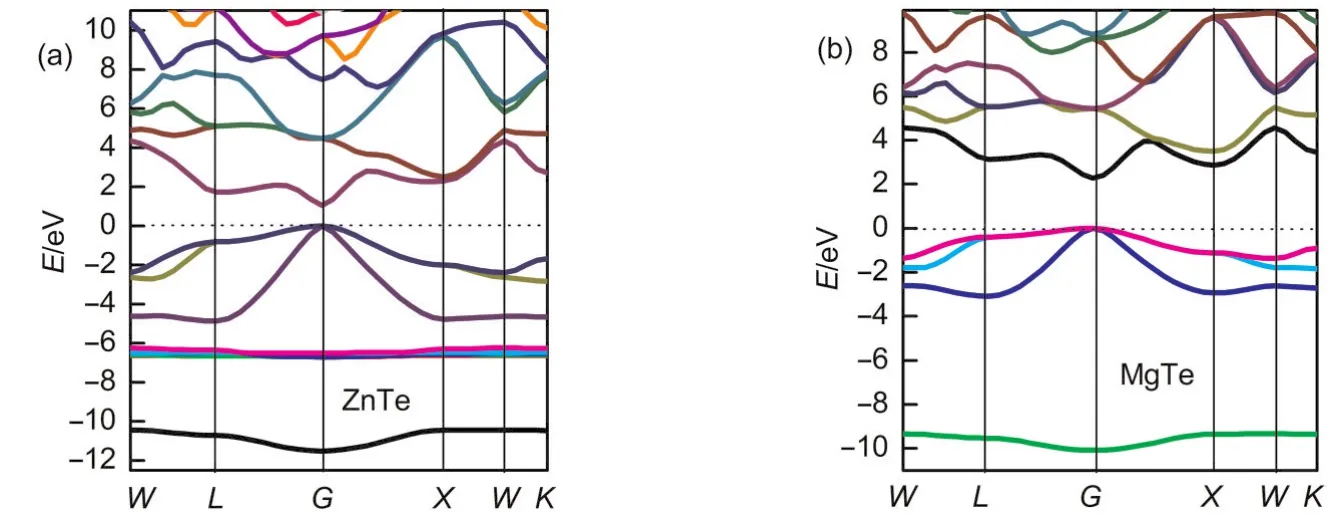
Fig.2 Electronic band structures of the ZnTe(a)and MgTe(b)compounds from GGAcalculations

Fig.2(a,b)shows the calculated electronic band structures along the high symmetry points in the Brillouin zone(BZ)for ZnTe and MgTe.Basically,the energy structure of crystals depends on the interactions between orbitals in the lattice.In both cases,the maximum valance band and minimum conduction band occur at theGpoint.The existence of a gap at Fermi level confirms the semiconductor character and indicates the respective presence of conducting features.The calculated band structure profiles for MTe(M=Mg/Zn)were similar except for the values of their band gaps.At the bottom,there are Tesbands exhibiting a weak dispersion.For ZnTe,a group of bands above thesband is composed of five Zndbands.Thesedbands are very narrow and show very little dispersion.The finite bandwidth results from thep-dhybridization with the Tepbands.38The bandwidth(i.e.,splitting)of Zn 3dlevels atGis 0.21 eV.Thisp-dcoupling exists,because in tetrahedral coordinated compounds(withTdsite symmetry)both the anionpand the cationdorbitals have the same representation atG.39These two equal-symmetry states can thus interact with each other,leading to consequent dramatic consequences(i)lower the band gaps,(ii)reduce the cohesive energy,(iii)increase the equilibrium lattice parameters and also have an influence on other features.

In Table 3,calculated direct and indirect band-gaps of MTe together with a few experimental40,41and published results3,42are summarized.The calculated minimum band gaps by GGA deviatefromtheexperimentalvalueswithin-51.7%and-34.0%for ZnTe and MgTe,respectively.However,they are in good agreement with other theoretical results.This underestimation of the band gaps is mainly due to the fact that the simple form of GGA neglects the quasiparticle self-energy which makes it not sufficiently flexible to accurately reproduce both exchange correlation energy and its charge derivative.43According to the data in the Table 3,the simulation results show that the B3LYP results are closer to the experimental data,and this method is more reasonable and precise than that of sX-LDAalgorithm.

In order to elucidate the major contribution of orbital in the band structure,the total and partial density of states(TDOS,PDOS)of these two compounds are calculated and shown in Fig.3.Likewise,a band gap at the Fermi level can be observed for the two crystals.The large peaks in the calculated TDOS from-7.0 to-6.0 eV for ZnTe and-42.6 to-41.6 eV for MgTe are mainly driven from Zn 3dand Mg 2porbitals,respectively.Additionally,the calculated PDOS of both ZnTe and MgTe crystals indicates that 5sand 5porbitals of Te are in low-lying states.Specially,a strong hybridization can be observed for ZnTe in the energy range between-7.0 and-6.0 eV due to an overlap with 3dorbital of Zn,which confirms the energy band structure analysis.The PDOS in Fig.3(a)indicate that conduction band minimum of ZnTe originate mainly from the cooperative contributions of Zn 4sand Te 5porbitals.For MgTe,the lower part of the valence bands is dominated by Te 5sstate,and upper part by Te 5p,Mg 3p,and Mg 3sstates.The first conduction band of MgTe consists mainly of Mg 3sand Mg 3pstates.

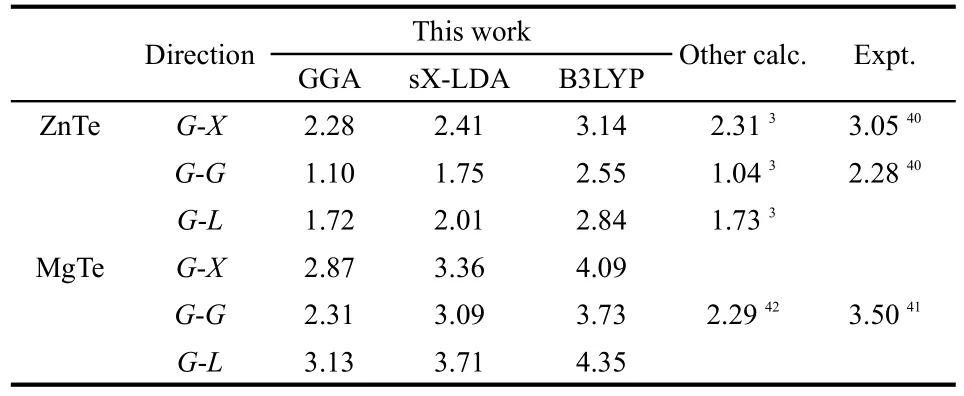
Table 3 Calculated energy band gap(eV)for MTe compounds compared to experimental and other theoretical works

In addition,we also calculated Mulliken populations for both ZnTe and MgTe on the grounds and this helps to understand bonding behavior,as listed in Table 4.In addition to providing an objective criterion for bonding between atoms,the overlap population may be used to assess the covalent or ionic nature of a bond.44The calculated overlap populations of Zn―Te and Mg―Te bonds are 0.43 and 0.09,respectively.It is clear that these values are positive,which means that both bonds are covalent.Bonding states may correlate with the relative high values of theB/Gof these two compounds.Moreover,Zn―Te bonds are more covalent than Mg―Te bonds due to the higher overlap population values.The bonding nature of MgTe may be described as a mixture of covalent-ionic,as mentioned above,and be partly metallic characters.In short,ZnTe with a valence state of Zn-0.18Te0.18is more covalent than MgTe with Mg0.51Te-0.51,while the ionicity of studied compounds decreases in the following sequence MgTe→ZnTe.

The bonding picture can be more vividly illustrated by plotting the charge density maps of specific crystallographic planes.The electron density distribution map is plotted in the way of the electron density difference map,as presented in Fig.4.The electron density difference was determined as Δρ={ρcrystal-Σρa(bǔ)tom},whereρcrystalandρa(bǔ)tomare the valence electron densities for MTe(M=Zn/Mg)and the corresponding free atoms,respectively.In general,many isolated atoms are connected together through such as chemical bond to form a solid and liquid.The electron density difference here denotes the difference in the electron density between the bonded atoms and the isolated atoms.This index allows visualizing the electron redistribution of the atoms after chemical bonding.It is obvious that the electron density on Zn―Te is stronger than that on Mg―Te,certificating that the covalence of Zn―Te is stronger than Mg―Te,which is coincided with the Mulliken population analysis.

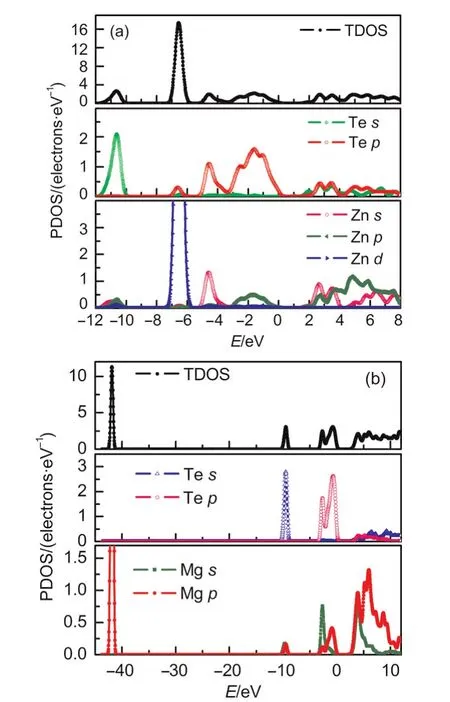
Fig.3 Calculated total density of state(TDOS)and partial density of state(PDOS)for ZnTe and MgTe compounds by GGA

Table 4 Mulliken populations of MgTe and ZnTe

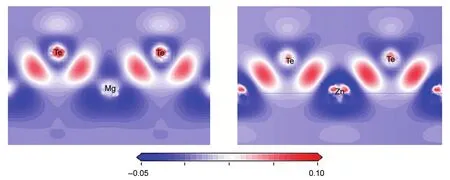
Fig.4 Electron density difference map of the plane containing M―Te bonds for MTe(M=Mg/Zn)plotted from-50 e·nm-3(blue)to 100 e·nm-3(red)

3.4 Optical properties

The optical properties are important for compounds under investigation,since they can find potential applications in photoelectron devices and the semiconductor industry.We already identify that the calculated direct band gap is smaller than the measured value,and the calculated dielectric function shifts towards lower energy.Hence,we amended bands gaps by using a scissor operator(scissor:ZnTe～1.18 eV,MgTe～1.19 eV).

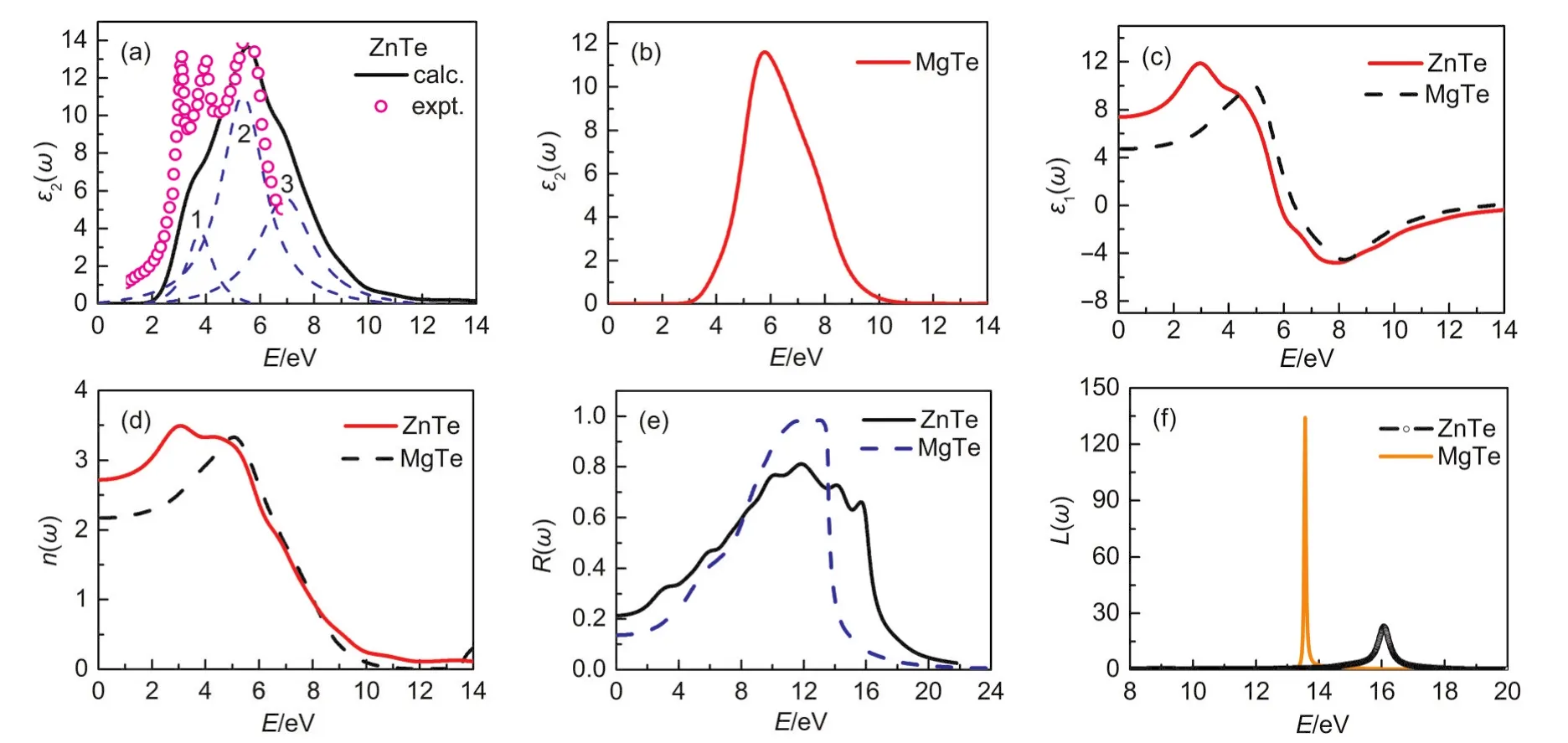
Fig.5 Calculated imaginary part ε2(ω)and real part ε1(ω)of the dielectric function ε(ω),refractive index n(ω),reflectivity spectrum R(ω),and energy loss spectrum L(ω)of MTe(M=Mg/Zn)

Table 5 Calculated refractive indices n and static dielectric constant ε for ZnTe and MgTe

The curves ofε2(ω)in Fig.5(a,b)indicate that the threshold energy(first critical point)of the dielectric function occurs at 2.26 and 3.48 eV for ZnTe and MgTe,respectively.These correspond to theGV-GCsplitting,for which evidence can be found in Fig.2,and give the threshold for direct optical transitions between the highest valence and the lowest conduction bands,which is known as the fundamental absorption edge.As illustrated in Fig.5(a),our calculatedε2(ω)for ZnTe reproduced qualitatively well the features observed in the experiment.45Additionally,three prominent peaks have been obtained by fitting theε2(ω)curve for ZnTe based on Lorenz function model:1(3.8 eV),2(5.0 eV),and 3(6.8 eV).Peak 1 mainly corresponds to the Te 4pVBs to the unoccupied CBs.Peaks 2 and 3 are assigned to the transition of inner electrons from Te 4sorbitals to the Zn 3dor Te 4pVBs,for which evidence can be found in the partial density of state(Fig.3(a)).The remarkable peak(5.7 eV)of MgTe in Fig.5(b)originates predominantly from the transitions of Te 4pelectrons into Mg 2pand 2sconduction bands.

The static dielectric constantεis given by the low energy limit ofε1(ω)as shown in Fig.5(c).Calculated values of the static macroscopic dielectric constants are given in Table 5.Unfortunately,as far as we know,there are no data available related to the static macroscopic dielectric constants in the literature for MTe(M=Zn/Mg),and this can serve as a prediction for future investigations.

The knowledge of the refractive indices of semiconductors is important in the design and analysis of heterostructure lasers and other wave-guiding semiconductor devices.Numerous semiempirical models have been proposed in the past years to model the refractive index of semiconductors below the lowest direct gap.46Such information forms an important part in the design of various optoelectronic devices.In this article,the refractive index(n)is also calculated using the Hervé and Vandamme empirical formula47which is related directly to the fundamental energy band-gapEgas

whereA=13.6 eV,B=3.4 eV,andEgis the lowest band gap.

The calculated refractive indices of studied compounds are investigated in Table 5.Note that our calculatednagrees well with the semi-empirical formul method,and also meet the ruleε≈n2,mentioned in literature.48In addition,a good agreement between the predicted value(2.717)and experimental49value(2.71)ofnfor ZnTe should confirm that our calculation method is reliable.

Fig.5(e)shows the results of the reflectivity functionR(ω)for the ZnTe and MgTe.The maximum reflectivity occurs in the energy regions of[10.9 eV,13.4 eV]and[10.0 eV,12.8 eV]for MgTe and ZnTe,respectively,and these are in the ultraviolet region.Therefore,the present results suggest that the two structures of MTe(M=Zn/Mg)materials can serve in optical devices such as shields for ultraviolet radiation.The electron energy loss functionL(ω)is an important factor describing the energy loss of a fast electron traversing in a material.Prominent peaks inL(ω)spectra represent the characteristics associated with the plasma oscillations and the corresponding frequencies are the so-called bulk plasma frequenciesω(p),which occurs whereε2＜1 andε1reaches zero point50.Obviously,one may note from the Fig.5(f)that the peaks ofL(ω)are located at about 13.58 and 16.04 eV for MgTe and ZnTe,respectively,which correspond to the abrupt reduction ofR(ω).

4 Conclusions

In summary,we have systematically studied the structural,elastic,electronic,and optical properties of the binary ZnTe and MgTe compounds in the zinc-blende phase using the first principles calculations based on a density functional PP-PW method with the GGA approximation.The choice of compounds was warranted by a great deal of attention given to these II-VI binaries because of their large field of applications.Some brief essential concluding remarks can be drawn below.

(1)The ground state properties such as lattice parameters,bulk modulus,and elastic constants were computed and compared with the experimental results which show good agreement.Both the investigated compounds are mechanically stable.

(2)TheB/Gvalues of MTe compounds show that both materials behave as ductile.The Debye temperatures for the investigated compounds are also reported for the first time.

(3)The bonding charge density calculations and the Mulliken population analysis reveal that the covalency of Zn-Te bonds are stronger than Mg-Te bonds and the chemical bonding in MgTe may be covalent-ionic.

(4)The electronic structure calculations show that MTe compounds in zinc-blende structure are direct band gap semiconductor materials.Compared to sX-LDA,B3LYP functional provides more accurate description for the electronic band structures of MTe.

(5)The imaginary and real parts of the dielectric function,the refractive index,reflectivity,and electron energy loss spectra are calculated.The static dielectric constantsεand refractive indexnhave been given.

(1) Kalpana,G.;Pari,G.;Bhattacharyya,A.K.Int.J.Mod.Phys.B1998,12,1975.doi:10.1142/S0217979298001149

(2) Triboulet,R.;Aulombard,R.L.;Mullin,J.B.Wide Gap II-VI Semiconductors:Proceedings of the E-MRSAdvanced Research Workshop;Adam Hilger:Montpellier,1991.

(3) Soykan,C.;Kart,S.O.J.Alloy.Compd.2012,529,148.doi:10.1016/j.jallcom.2012.02.170

(4) Drief,F.;Tadjer,A.;Mesri,D.;Aourag,H.Catal.Today2004,89,343.doi:10.1016/j.cattod.2003.12.013

(5) Joshi,K.B.;Pandya,R.K.;Kothari,R.K.;Sharma,B.K.Phys.Status Solidi B2009,246,1268.doi:10.1002/pssb.v246:6

(6) Kanoun,M.B.;Merad,A.E.;Aourag,H.;Cibert,J.;Merad,G.Solid State Sci.2003,5,1211.doi:10.1016/S1293-2558(03)00154-7

(7) Duan,H.;Chen,X.S.;Sun,L.Z.;Zhou,X.H.;Lu,W.Acta Phys.Sin.2005,54,5293.[段 鶴,陳效雙,孫立忠,周孝好,陸 衛(wèi).物理學(xué)報(bào),2005,54,5293.]

(8) Khenata,R.;Bouhemadou,A.;Sahnoun,M.;Reshak,A.H.;Baltache,H.;Rabah,M.Comput.Mat.Sci.2006,38,29.doi:10.1016/j.commatsci.2006.01.013

(9) Palomino-Rojas,L.A.;Cocoletzi,G.H.;de Coss,R.;Takeuchi,N.Solid State Sci.2009,11,1451.doi:10.1016/j.solidstatesciences.2009.04.030

(10) Chaudhuri,C.B.;Pari,G.;Mookerjee,A.;Bhattacharyya,A.K.Phys.Rev.B1999,60,11846.doi:10.1103/PhysRevB.60.11846(11) Varshney,D.;Kaurav,N.;Sharma,U.;Singh,R.K.J.Phys.Chem.Solids2008,69,60.doi:10.1016/j.jpcs.2007.07.121

(12) Franco,R.;Mori-Sánchez,P.;Recio,J.M.;Pandey,R.Phys.Rev.B2003,68,195208.doi:10.1103/PhysRevB.68.195208

(13) Gupta,S.K.;Kumar,S.;Auluck,S.Physica B2009,404,3789.doi:10.1016/j.physb.2009.06.149

(15)Kohn,W.;Sham,L.J.Phys.Rev.1965,140,1133.

(16) Payne,M.C.;Teter,M.P.;Allan,D.C.;Arias,T.A.;Joannopoulos,J.D.Rev.Mod.Phys.1992,64,1045.doi:10.1103/RevModPhys.64.1045

(17) Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77,3865.doi:10.1103/PhysRevLett.77.3865

(18) Vanderbilt,D.Phys.Rev.B1990,41,7892.doi:10.1103/PhysRevB.41.7892

(19) Fischer,T.H.;Almlf,J.J.Phys.Chem.1992,96,9768.doi:10.1021/j100203a036

(20)Lee,B.;Wang,L.W.;Spataru,C.D.;Louie,S.G.Phys.Rev.B2007,76,245114.doi:10.1103/PhysRevB.76.245114

(21) Stephens,P.J.;Devlin,F.J.;Chabalowski,C.F.;Frisch,M.J.J.Phys.Chem.1994,98,11623.doi:10.1021/j100096a001

(23) Zhang,Z.Y.;Yang,D.L.;Liu,Y.H.;Cao,H.B.;Shao,J.X.;Jing,Q.Acta Phys.-Chim.Sin.2009,25,1731.[張子英,楊德林,劉云虎,曹海濱,邵建新,井 群.物理化學(xué)學(xué)報(bào),2009,25,1731.]doi:10.3866/PKU.WHXB20090819

(24) Jiao,Z.Y.;Ma,S.H.;Yang,J.F.Solid State Sci.2001,13,331.

(25) O'Donnell,M.;Jaynes,E.T.;Miller,J.G.J.Acoust.Soc.Am.1981,69,696.doi:10.1121/1.385566

(26) Birch,F.Phys.Rev.1947,71,809.doi:10.1103/PhysRev.71.809

(27) Ley,L.;Pollak,R.A.;Mcfeely,F.R.;Kowalczy,S.P.;Shirley,D.A.Phys.Rev.B1974,9,600.doi:10.1103/PhysRevB.9.600

(28) Hartmann,J.M.;Cibert,J.;Kany,F.;Mariette,H.;Charleux,M.;Alleysson,P.;Langer,R.;Feuillet,G.J.Appl.Phys.1996,80,6257.doi:10.1063/1.363714

(29) Cohen,M.L.Phys.Rev.B1985,32,7988.doi:10.1103/PhysRevB.32.7988

(30) Zubov,V.I.;Tretiakov,N.P.;Rabelo J.N.T.;Ortiz,J.F.S.Phys.Lett.A1994,194,223.doi:10.1016/0375-9601(94)91288-2

(31) Korozlu,N.;Colakoglu,K.;Deligoz,E.;Aydin,S.J.Alloy.Compd.2013,546,157.doi:10.1016/j.jallcom.2012.08.062

(32) Lee,B.H.J.Appl.Phys.1970,41,2988.doi:10.1063/1.1659350

(33) Push,S.F.Philos.Mag.1954,45,823.

(34) Nye,J.F.Physical Properties of Crystals;Oxford University Press:Oxford,1985;Vol.2.

(35) Christman,J.R.Fundamentals of Solid State Physics;John Wiley&Sons:New York,1988.

(36)Anderson,O.L.J.Phys.Chem.Solids1963,24,909.

(37)Varshney,D.;Shriya,S.;Khenata,R.Mater.Chem.Phys.2012,135,365.doi:10.1016/j.matchemphys.2012.04.060

(38) Lee,G.D.;Lee,M.H.;Ihm,J.Phys.Rev.B1995,52,1459.doi:10.1103/PhysRevB.52.1459

(39) Merad,A.E.;Kanoun,M.B.;Merad,G.;Cibert,J.;Aourag,H.Mater.Chem.Phys.2005,92,333.doi:10.1016/j.matchemphys.2004.10.031

(40)Maksimoy,O.;Tamargo,M.C.Appl.Phys.Lett.2001,79,782.doi:10.1063/1.1390327

(41) Parker,S.G.;Reinberg,A.R.;Pinnell,J.E.;Holton,W.C.J.Electrochem.Soc.1971,118,979.doi:10.1149/1.2408236

(42) Fleszar,A.Phys.Rev.B2001,64,245204.doi:10.1103/PhysRevB.64.245204

(43)Rashkeev,S.N.;Lambrecht,W.R.L.Phys.Rev.B2001,63,165212.doi:10.1103/PhysRevB.63.165212

(44)Wang,Y.F.;Gao,J.K.;Lee,M.H.;He,W.;Xu,X.;Hao,L.Y.;Chen,J.H.Chin.J.Chem.Phys.2012,25,398.doi:10.1088/1674-0068/25/04/398-402

(45)Bang,C.Y.;Lee,M.S.;Kim,T.J.;Kim,Y.D.Aspnes,D.E.;Yu,Y.M.;O,B.S.;Choi,Y.D.J.Korean Phys.Soc.2001,39,462.

(46) Lee,D.;Johnson,A.M.;Zucker,J.E.;Burrus,C.A.;Feldman,R.D.;Austin,R.F.IEEE Photonics Technol.Lett.1992,4,949.doi:10.1109/68.157111

(47) Hervé,P.J.L.;Vandamme,L.K.J.J.Appl.Phys.1995,77,5476.doi:10.1063/1.359248

(48) Samara,G.A.Phys.Rev.B1983,27,3494.doi:10.1103/PhysRevB.27.3494

(49) Marple,D.T.F.J.Appl.Phys.1964,35,539.doi:10.1063/1.1713411

(50) deAlmeida,J.S.;Ahuja,R.Phys.Rev.B2006,73,165102.doi:10.1103/PhysRevB.73.165102