Method of variation of parameters for solving a constrained Birkhoffian system

Zhang Yi

(College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China)

The theory of integration for the constrained mechanical systems is an important aspect of the research for analytical dynamics. A set of beautiful methods of integration for conservative systems encountered great difficulties in reaching out to nonconservative, or nonholonomic dynamics. Therefore, it is an important research direction for analytical dynamics in providing the new versatile method of integration to complex dynamical systems. The Birkhoffian system is a quite extensive class of the dynamical system, and it is a generalization of the Hamiltonian system. The theory of integration for the Birkhoffian system is an important part of Birkhoffian dynamics[1]. The US physicist Santilli[2]studied the Birkhoff equations, the theory of transformation of the Birkhoff equations and the generalization of Galilei relativity in his monograph, and extended the Hamilton-Jacobi method to the Birkhoffian system. Galiullan et al.[3]studied the inverse problem of Birkhoffian dynamics, the integral invariants of the Birkhoffian system, and the conformal invariance etc. Mei[1,4-7]established the Poisson theory of the Birkhoffian system, the field method for integrating the Birkhoff equations, the symmetries and the conserved quantities, the inverse problems of dynamics and the integral invariants, and extended them to the generalized Birkhoffian system. Zhang[8]provided the method of variation of parameters for integrating the generalized Birkhoffian system. In recent years, some important results on the research of the theory of integration for Birkhoffian systems have been obtained[9-18].In this paper, we will further apply the method of variation of parameters for solving the integration issues of the constrained Birkhoffian system. The method is of universal importance, and it reveals the inherent relationship between the solution of a free Birkhoffian and that of a constrained Birkhoffian system.

1 Differential Equations of Motion for a Cons-trained Birkhoffian System

The Birkhoff equation in the general form of a Birkhoffian system is[1-2]

(1)

whereB=B(a,t) is called Birkhoffian;Rμ=Rμ(a,t) is the Birkhoff function.

Suppose that the variablesaμ(μ=1,2,…,2n) of system (1) are not independent of each other, but they are restricted by some constraints, and, as such, the system is called a constrained Birkhoffian system. If the restrictions can be expressed as the following constraint equations

fβ(a,t)=0β=1,2,…,g

(2)

then the restrictions added to the virtual displacements by constraints (2) are

(3)

The differential equations of motion with multipliers of the constrained Birkoffian system can be expressed as[1]

(4)

Considering that the system is non-singular and from Eqs.(2) and (4), we can seekλβas the function of (a,t) before integrating the differential equations of motion. Therefore, Eq.(4) can further be written as

(5)

where

ΩμνΩντ=δμτ, det(Ωμν)≠0

(6)

Eq.(5) is called the differential equations of motion for the free Birkhoffian system which corresponds to the constrained Birkhoffian systems (2) and (4). As long as the initial conditions of motion satisfy the constraint equation (2), the solution of the corresponding free system (5) gives the motion of the constrained Birkhoffian system.

2 Method of Variation of Parameters for a Con-strained Birkhoffian System

To solve the constrained Birkhoffian system with the method of variation of parameters, we build a system of auxiliary equations as

(7)

Let the general solution of Eq.(7) be

aμ=aμ(α1,α2,…,α2n,t)μ=1,2,…,2n

(8)

whereαμis an integral constant which is the value ofaμwhent=0. Without loss of generality, we takeαμas a new variable, make a variable substitution according to Eq.(8), and select

(9)

We can easily obtain[2]

(10)

Therefore, the transformation (8) is a generalized canonical transformation, and we have[2]

(11)

Suppose that the inverse transformation of the transformation (8) is

αμ=αμ(a1,a2,…,a2n,t)μ=1,2,…,2n

(12)

Since Eq.(12) is the first integral of Eq.(7), we have

(13)

Then, we find a general solution of Eq.(5).

Assume that the solution of Eq.(5) still has the form of Eq.(8), andαμis no longer a constant but a function of timet. Differentiating the formula (12) with respect to timet, we obtain

(14)

From Eq.(11), Eq. (14) can be written as

(15)

Hence, we have

(16)

(17)

The solution of the constrained Birkhoffian systems (2) and (4) under consideration is found by combining (16) and (17), which contains 2n-gindependent constants. Therefore, we obtain the following proposition.

3 Example

The BirkhoffianBand the Birkhoff functionsRμof a four-dimensional Birkhoffian system are respectively

R1=a3,R2=a4,R3=R4=0

(18)

whereg,φare constants. The constraint equations are

f1=a1-a2=0,f2=a3-2a4=0

(19)

We try to solve this problem by the method of this paper.

In order to solve this problem, we divide it into two steps. First, let us establish an auxiliary system and solve it. The auxiliary equation (7) gives that

(20)

The solution of Eq.(20) is

a3=α3+gtsinφ,a4=α4

(21)

whereαμ(μ=1,…,4) are constants of integration.

Choose

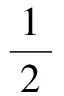
(22)

We can easily verify the validity of Eq.(10).

Secondly, let us give a variation of parameters and calculate the motion of the system. Eq.(4) gives that

(23)

From Eqs.(23) and (19), we can obtain

(24)

Therefore, we have

(25)

Eq.(15) gives that

(26)

Integrating Eq.(26), we have

(27)

Substituting (27) into (21), we obtain

(28)

Eq.(28) is the solutions of the corresponding free Birkhoffian system. Substituting the inertial conditions into the constraint equation (19), we have

(29)

Eqs.(28) and (29) give the general solution of the problem under consideration, and it contains two arbitrary constants. For this problem, we can verify that its solution is given by Eqs.(28) and (29) through direct calculation.

4 Conclusion

The constrained Birkhoffian systems are a broad class of dynamical systems. The method of variation of parameters for solving the generalized Birkhoffian system is extended to the constrained Birkhoffian system in this paper. By means of this method, we can integrate a constrained Birkhoffian system in two steps. In the first step, we can construct a system of auxiliary equations whose solution is known. In the second step, we can vary the parameters, and the problem is reduced to solving Eq.(15). The research results of this paper are of universal significance, which can be applied to the systems with holonomic and nonholonomic constraints.

[1]Mei F X, Shi R C, Zhang Y F, et al.DynamicsofBirkhoffiansystems[M]. Beijing: Beijing Institute of Technology Press, 1996. (in Chinese)

[2]Santilli R M.FoundationsoftheoreticalmechanicsⅡ [M]. New York: Springer-Verlag, 1983.

[3]Galiullin A S, Gafarov G G, Malaishka R P, et al.AnalyticaldynamicsofHelmholtz,BirkhoffandNambusystems[M]. Moscow: UFN, 1997. (in Russian)

[4]Mei F X. Noether theory of Birkhoffian system [J].ScienceinChina:SeriesA, 1993,36(12): 1456-1467.

[5]Mei F X. Poisson’s theory of Birkhoffian system [J].ChineseScienceBulletin, 1996,41(8): 641-645.

[6]Mei F X, Wu H B. First integral and integral invariant of Birkhoffian system [J].ChineseScienceBulletin, 2000,45(5): 412-414.

[7]Mei F X. On the Birkhoffian mechanics [J].InternationalJournalofNon-LinearMechanics, 2001,36(5): 817-834.

[8]Zhang Y. The method of variation on parameters for integration of a generalized Birkhoffian system [J].ActaMechanicaSinica, 2011,27(6):1059-1064.

[9]Guo Y X, Shang M, Luo S K. Poincaré-Cartan integral variants of Birkhoff system [J].AppliedMathematicsandMechanics, 2003,24(1): 76-82.

[10]Guo Y X, Liu C, Liu S X. Generalized Birkhoffian formulation of nonholonomic systems [J].CommunicationsinMathematics, 2010,18(1): 21-35.

[11]Luo S K, Guo Y X. Routh order reduction method of relativistic Birkhoffian systems [J].CommunicationinTheoreticalPhysics, 2007,47(2): 209-212.

[12]Mei F X, Wu H B. Form invariance and new conserved quantity of generalized Birkhoffian system [J].ChinesePhysicsB, 2010,19(5): 050301.

[13]Li Y M. Lie symmetries, perturbation to symmetries and adiabatic invariants of a generalized Birkhoff system [J].ChinesePhysicsLetters, 2010,27(1): 010202.

[14]Zhang Y. Poisson theory and integration method of Birkhoffian systems in the event space [J].ChinesePhysicsB, 2010,19(8): 080301.

[15]Zhang M J, Fang J H, Lu K. Perturbation to Mei symmetry and generalized Mei adiabatic invariants for Birkhoffian systems [J].InternationalJournalofTheoreticalPhysics, 2010,49(2): 427-437.

[16]Zhang Y, Zhou Y. Symmetries and conserved quantities for fractional action-like Pfaff variational problems [J].NonlinearDynamics, 2013,73(1/2): 783-793.

[17]Zhang Y. A new method for integration of a Birkhoffian system [J].JournalofSoutheastUniversity:EnglishEdition, 2011,27(2): 188-191.

[18]Wu H B, Mei F X. Type of integral and reduction for a generalized Birkhoffian system [J].ChinesePhysicsB, 2011,20(10): 104501.