Modeling and Numerical Simulation of Yield Viscoplastic Fluid Flow in Concentric and Eccentric Annuli*

MAO Zaisha (毛在砂)**, YANG Chao (楊超) and Vassilios C. Kelessidis2 Key Laboratory of Green Process and Engineering, Institute of Process Engineering, Chinese Academy of Sciences,Beijing 0090, China

2 Mineral Resources Engineering Department, Technical University of Crete, Greece

1 INTRODUCTION

In oil-well drilling, drilling fluids are used for a variety of function such as transporting the rock cuttings from the well bottom to the surface, providing hydraulic pressure, cooling the bit, etc. Various models are used to describe the rheological behavior of drilling fluids, including two parameter Bingham plastic model, power law model and three parameter models such as Herschel-Bulkley model, Carreau model and many others. For more description of these rheological models, the readers are referred to monographs like Bird et al. [1] and Chhabra [2].

As for the applications to drilling fluids, Kelessidis et al. [3] and many others used the Herschel-Bulkley model to represent their experimental data on the behavior of shear stress with shear rate:

where τ and τyare the shear stress and the yield stress respectively, K and n are the fluid consistency and fluid behavior index respectively, and γ is the shear rate in fluid. Their experiments [3, 4] were on waterbentonite suspensions with and without lignite from different places in Greece as thinning agent. Kelessidis et al. found that the Hershel-Bulkley model can effectively correlate the rheological data of several drilling fluids and proposed an improved method for determining the Herschel-Bulkley model parameters[3]. Although the argument on whether the yield stress really exists, the 3-parameter Herschel-Bulkley model is popularly used among petroleum industry practitioners [5].

Driven by the demand of knowledge on non-Newtonian fluid flow, many experimental studies on rheological behaviors and transport phenomena have been conducted in last decades. Due to the difficulty in conducting three-dimensional measurements and less developed measurement techniques for turbid and opaque fluids, numerical simulation approaches display gradually their advantages in conceiving the details of flow pattern and property distribution, which are not straightforwardly available just by experimental measurements. Numerical simulation of non-Newtonian fluid flow has been advanced to a sophisticated level and plays an important role in understanding the non-Newtonian fluid flow and guiding the industrial operation related with such fluids. Recent publications reviewed such technical progresses in numerical simulation of non-Newtonian fluid flows [5, 6].

In general, the constitutive equation of Herschel-Bulkley fluids presents great obstacles for numerical simulation of their flow and transport phenomena due to the discontinuity in Eq. (1). Actually, Eq. (1) applies only when γ＞0, while τ is indefinite between 0 and τywhen γ=0. This makes the stress and apparent viscosity μ(γ) discontinuous at γ=0 [μ(γ)→∞ as γ→0].To bypass this difficulty, other rheological constitutive equations without discontinuity are proposed. Among them, Papanastasiou [7] proposed the continuous viscoplastic approximation (CVA) for Bingham fluids to make the apparent viscosity be finite at γ→0:For Hershel-Bulkley fluids, its analog is

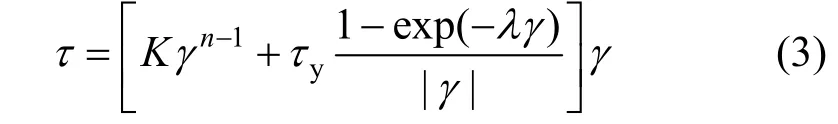
If parameterλis chosen sufficiently large, Eq. (3) becomes continuous and smooth, and the deviation from Eq. (1) occurs only in a small range very close toγ ～0,as illustrated in Fig. 1. This treatment makes the discontinuity of apparent viscosity,

atγ→0 reduces from a high order infinity to a lower order one offor 0＜n＜1 of drilling fluids.

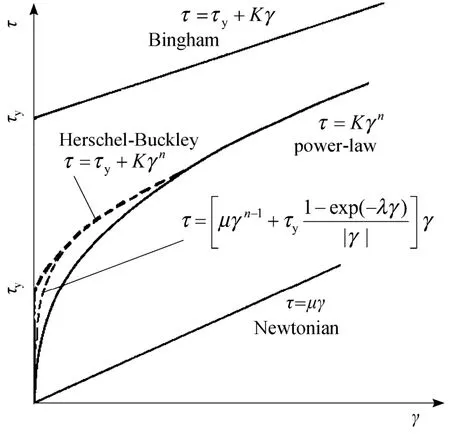
Figure 1 Non-Newtonian liquids with different rheological behaviors

CVA is popularly adopted by many authors in their numerical work on simulating the behaviors of Herschel-Bulkley fluids. For example, Papanastasiou and Boudouvis investigated numerically using CVA the flow structure in square, rectangular ducts and elliptic annular dies [8]. Hussain and Sharif [9] simulated the helical flow of yield viscoplastic fluids in eccentric annuli using the Papanastasiou’s modification of the Herschel-Bulkley constitutive equation, but the simulation was not compared with experiment because of lack of experimental data.

Another way of approximation is the so-called biviscosity model: the apparent viscosity is set to a constant of high value when the shear rate falls below a certain low level, while above the threshold the visco-plastic property is correctly expressed by the constitutive equation [10, 11]. Since the two regions do not connect smoothly, its applicability is expected to be even more awkward than CVA.

In this work, we propose a strict mathematical formulation of fully developed axial laminar flow of a Herschel-Bulkley fluid in concentric and eccentric annuli based on the control volume formulation on a boundary-fitted coordinate system. The algorithm for numerical solution is proposed. In view of the numerical difficulty in getting the converged general flow structure in both the yielded (shearing flow) and unyielded (plug flow) regions, some special structures meeting the governing equations and the boundary conditions on the boundary between two regions are conceived and tested. An alternative numerical strategy is explored to resolve the flow in a concentric annulus through optimization of parameters of a presumed flow structure. The challenges for the numerical solution in eccentric annulus and mathematical description of temporal development of Herschel-Bulkley fluid flow are briefly addressed.

2 FORMULATION OF HERSCHEL-BULKLEY FLUID IN ANNULUS

2.1 Physical conception

A Herschel-Bulkley fluid will not flow in an annular conduit, unless the shear stress at the external and internal walls is above the yield stress. As the fluid starts to flow, not the whole cross section has the shear rate above the value ofτy, so that the fluid in some region does not yield and it would move like a plug flow of unyielded soft solid. The typical situation is depicted in Fig. 2. In regionA, the fluid flows as driven by the pressure drop, and the flow is governed by the general continuity and momentum balance equations. In the plug flow regionsBandC, the fluid moves along with the yielded fluid as solid block, which is governed by the solid mechanical laws, with the strain induced by the same pressure drop. The deformation can be reasonably perceived as elastic such that the Hooke law would apply. At the boundary between these two regions, the balance between the yield shear stress and the elastic stress exists as the boundary condition. Thus, the fluid mechanical and solid mechanical equations will be solved in a coupled way. The detailed formulation will be described in the following sections.

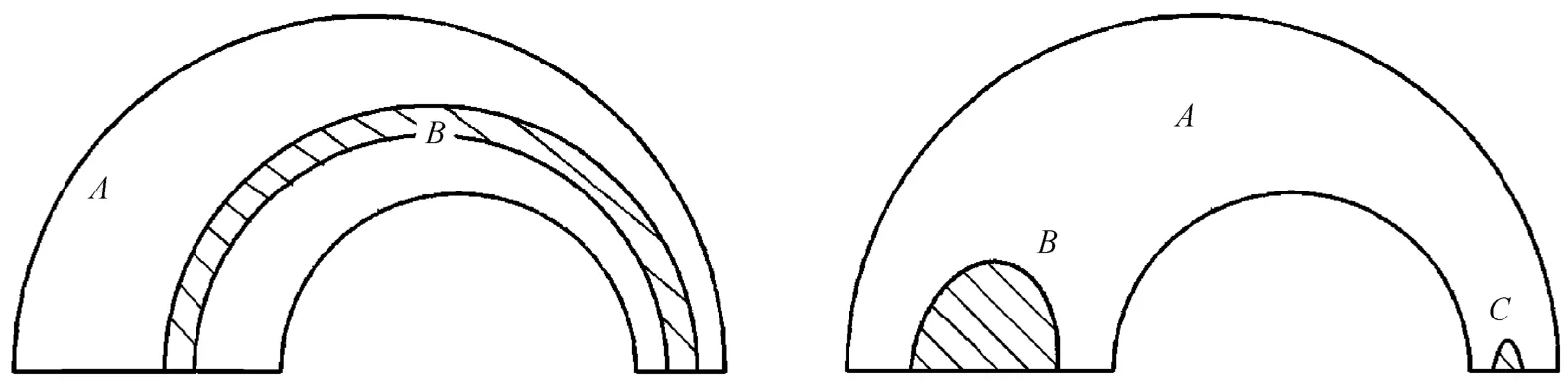
Figure 2 Feasible flow structure in an eccentric annulus with plug flow regions A—shear flow region (0γ＞), B, C—unyielded region (plug flow) (0γ=)

2.2 Governing equations in the yielded region

The yield viscoplastic fluid flow in a pipe or annulus is usually modeled based on the assumptions such as (1) the fluid is incompressible and isothermal and (2) the flow is laminar, steady and fully developed.Thus, the mathematical formulation of steady laminar flow of fluid may be expressed in general as

However, the stress tensorτis nonlinearly related to the rate of strain for non-Newtonian fluids. As the present viscoplastic fluid flow is concerned, the rheological equation in one-dimensional axial flow is represented by the Herschel-Bulkley model, Eq. (1).

If one-dimensional, fully-developed flow in a straight pipe or annulus depicted in Fig. 3 is considered, only the axial velocity componentw(x,y) is non-trivial and needs to be solved over the cross section. In this case, Eq. (5) of continuity is satisfied automatically, and the left-hand side of Eq. (6) turns out to be zero identically. The pressure changes only along thezaxis and the pressure drop dp/dzis a constant. Therefore, the governing equation becomes

in whichizis the unit vector in thezdirection. The shear stress tensor will be invariant in thezdirection and only two non-zero components survive therein:and its divergence is

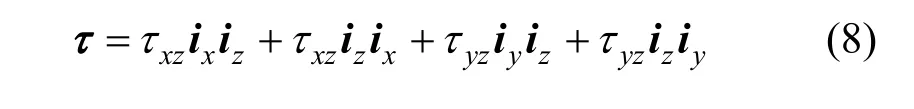
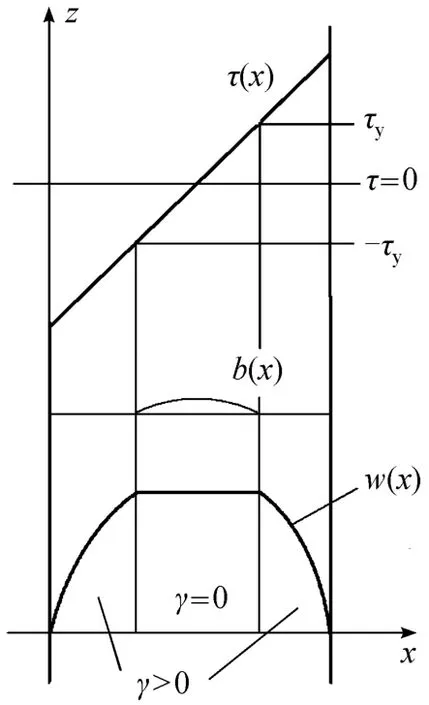
Figure 3 Sketches of velocity profile and stress distribution across the annulus

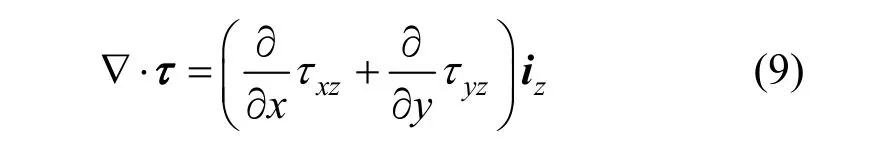
Thus, the governing momentum equation (6) in thezdirection is simplified to

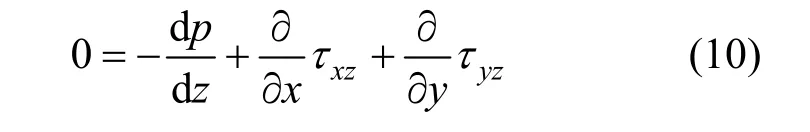
To get the solution of fluid flow and the area of each region, accurate enforcement of boundary conditions is necessary. Foreseeing the complex shape of the plug flow region, the boundary-fitted coordinate system is adopted to suit for the varying eccentricity of annulus,e:

and the momentum equation (10) is to be solved on a transformed computational domain in theξ-o-ηcoordinate system as depicted in Fig. 4. The annulus in the physical coordinate systemx-o’-yis transformed into a rectangle in the computational plainξ-o-ηby the orthogonal transformation. In the latter reference frame the domain boundaries are in coincidence with the coordinate axes so that the physical boundary conditions can be enforced more easily and accurately.

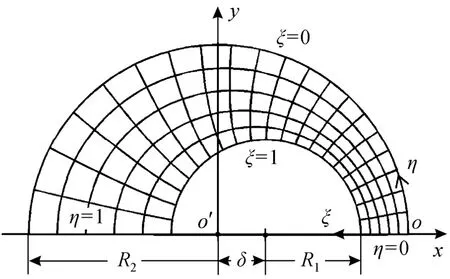
Figure 4 Sketch of eccentric annulus in physical x-o′-y system and computational orthogonal boundary-fitted ξ-o-η coordinate system

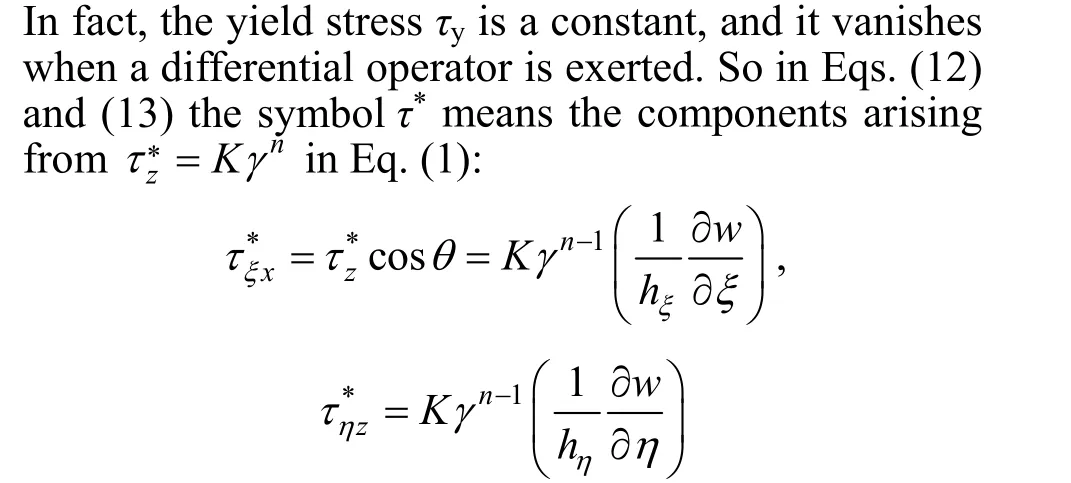
Equation (12) demands that the constant pressure drop is balanced by the net shear force over a rectangular cell as demarked by dotted lines in Fig. 5, meanwhile the shear force is decided through Eq. (13). The momentum balance Eq. (12) will be eventually transformed into a partial differential equation of velocity componentw(ξ,η) to be solved in the yielded flow region.

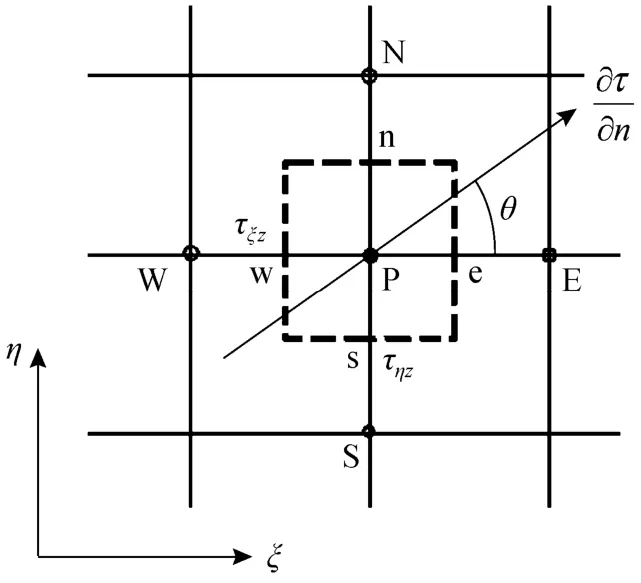
Figure 5 Typical cell (dotted line enclosed) around node P for velocity w

2.3 Numerical scheme for Eq. (12)

The numerical solution is based on a general finite difference method, particular the control volume formulation described by Patankar [12]. Eq. (12) is integrated over the control volume in Fig. 5 to get

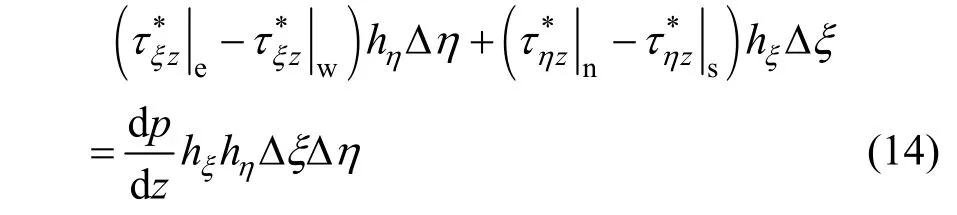
The rheological relation of yield viscoplastic fluid is nonlinear, thus it is not easy to convert Eq. (12)to an algebraic equation of velocity componentw(ξ,η).In this work, the linearization technique is applied to Eq. (14), and the following expressions of two shear stress components are obtained:

The discretized expressions forzξτat the east and west faces of cellPare Substituting the above linearized expressions into Eq.(14) leads to

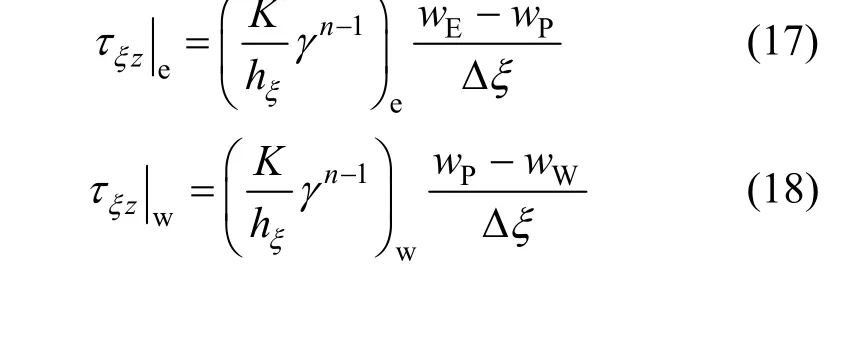
It is then rearranged to the general form of discrete equation as usually done in the control volume approach [12]:in which the following coefficients and source term are defined:

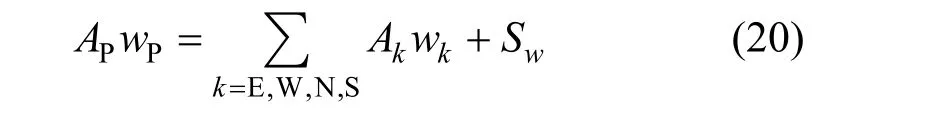
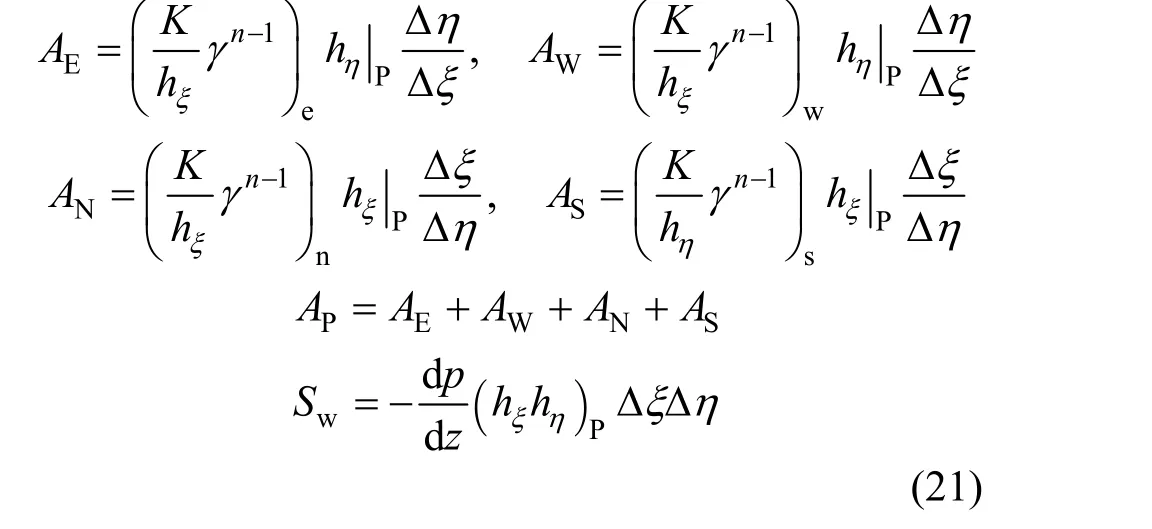
whereξΔ,ηΔ are the side length of a control volume in theξandηdirections. In above, the capital letter subscripts are indices to neighbor nodes and the lower case ones to the cell faces, as illustrated in Fig. 5.

As for the boundary conditions, no slip condition(w=0) at the solid walls is to be satisfied. On the boundary to the unyielded region, the magnitude ofτzapproachesτy, the rate of shear approaches 0 (γ→0),namely

In the present case of 1D axial flow normal to the cross section in Fig. 4 where the only non-zero velocity component isw(ξ,η), the magnitude of shear rate is

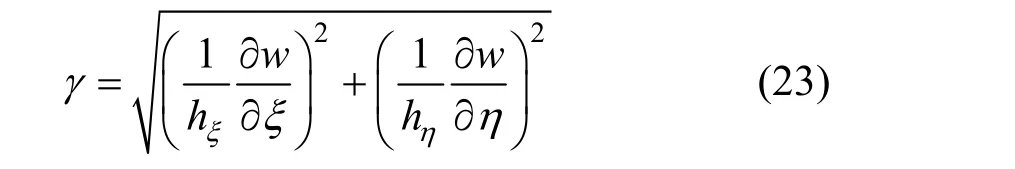
If the driving force of flow, -dp/dz, is specified,the solution ofw(x,y) from Eq. (20) would proceed in an iteration loop because the coefficients in Eq. (20)need to be updated from the just resolved w(x, y) field due to the non-linearity.

2.4 Governing equation of the unyielded region

When the shear stress is below the yield stressyτ,the fluid elements in the plug flow region are static relative to one another and each of them is subjected to the axial force balance. The plug flow region is exerted the pressure drop in the z direction so that elastic strain stress may occur as described by the force balance:

in which τ stands for the stress tensor resulted from elastic deformation of fluid. The stress is controlled by the general Hooke’s law:

where G is the elasticity modulus of the unyielded state and B the finger strain tensor [8]. For fully developed axial flow, Eq. (24) reads

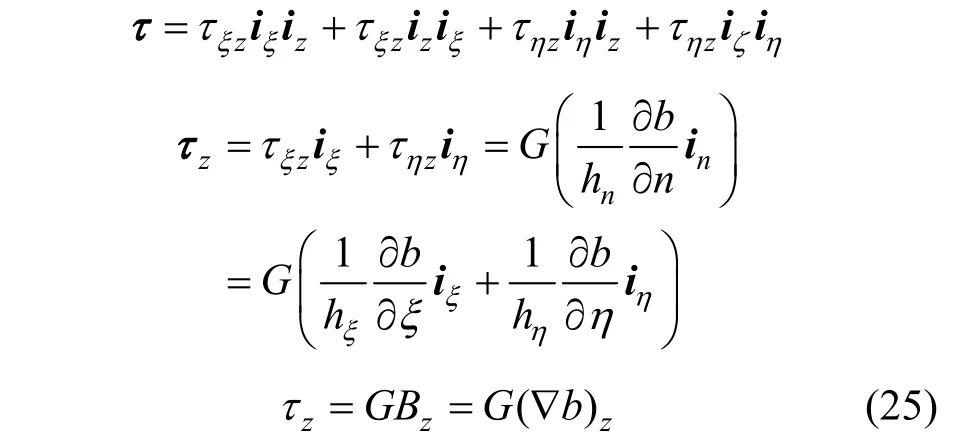
where subscript n indicates the direction of gradient of elastic deformation b(ξ, η). With Eq. (25) substituted into Eq. (7), we get

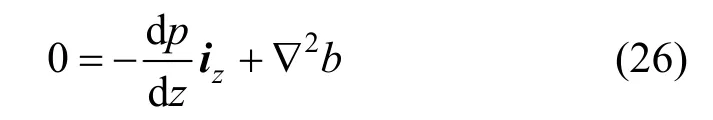
With the Laplacian operator in the (ξ, η, z) reference frame:

substituted, we finally get the partial differential equation for the elastic deformation b(ξ, η):

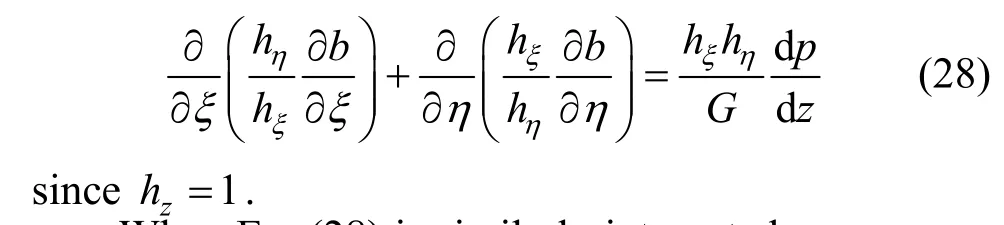
When Eq. (28) is similarly integrated over a control volume as Eq. (12) being treated, the following discretized algebraic equation is resulted:

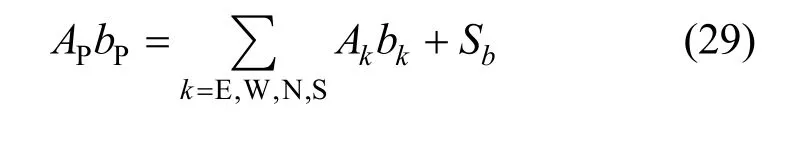
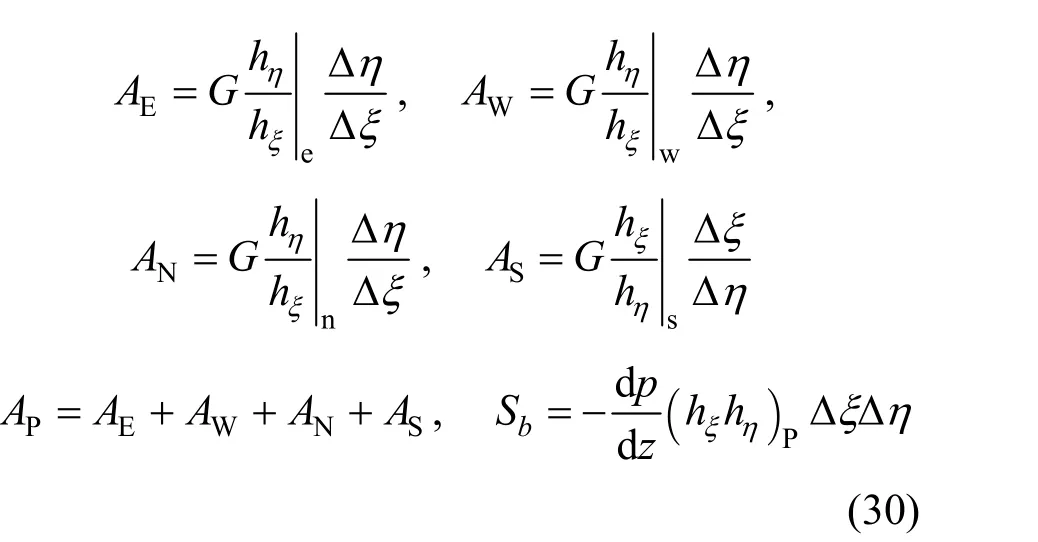
Equation (28) or (29) is the governing equation for elastic deformtion in the region of 0γ=. By solving it we get the fluid strain b(ξ, η), which is in fact a tiny elastic deformation. The stresszτ is evaluated from b(ξ, η), and it should be linearly distributed in the unyielded region betweenyτ- andyτ since the driving force on the left hand of Eq. (28) is a constant dp/dz, as indicated in Fig. 3.

However, the shear stress at the borders of regions B and C in Fig. 2 is always equal toyτ, and balanced by the pressure drop which drives the fluid to flow.This is indeed the boundary condition to be satisfied between the yielded and unyielded regions, namely

On the symmetry axis, zero derivative of b is to be enforced. With these boundary conditions, the twodimensional distribution of b(ξ, η) and τ(ξ, η) in the plug flow region can be resolved.

2.5 Boundary-fitted coordinate system

Eccentric annulus is geometrically complex and it is not convenient to perform numerical simulation in such a domain. A boundary-fitted orthogonal curvilinear coordinate system is beneficial to the numerical solution in this case because the boundary conditions at the outer and inner walls can be enforced more easily and accurately. The covariant Laplacian equations

are utilized to transform the physical domain of an eccentric annulus into a unit square (0≤ξ≤1, 0≤η≤1)in the computational plane (ξ, η) as indicated in Fig. 4.Orthogonal mapping is carried out by the methods proposed by Ryskin and Leal [13], and this technique was used successfully in our previous work [14, 15].The distortion function f(ξ, η) is defined as the ratio of scaling factors in the ξ and η directions to symbolize the aspect ratio of a cell in the physical (x, y) plane:

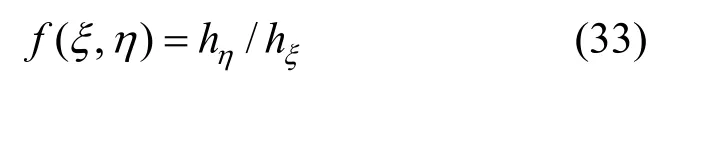
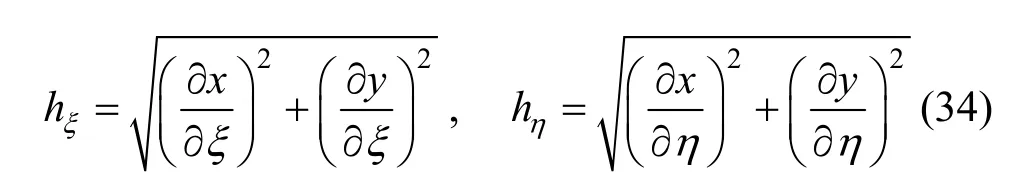
With proper boundary conditions relating the physical and computational domains, the numerical grids are generated by solving Eq. (32) using the finite difference method.

In the present case, we use the strong constraint method [13] to create the orthogonal grid, namely, the distortion functionf(ξ,η) is apriorispecified as

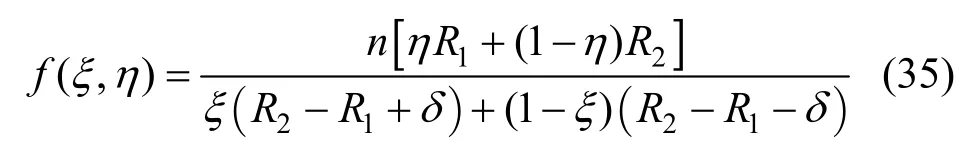
which is essentially an expression of Eq. (33) when a grid with nodes inξandηdirections being uniformly distributed in the square of (0≤ξ≤1, 0≤η≤1). This is a tolerable choice in the typical case ofR2/R1=2 ande=δ/(R2-R1)=0.5, the local maximum of mesh non-orthgonality on a 41×41 grid,

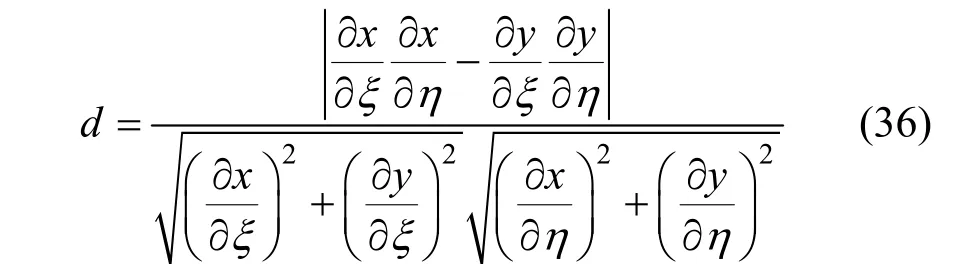
is only 0.010, which is equivalent that two coordinate lines intersect at the node with the angle of 89.43°,and the averagedover all nodes is 0.0045.

3 NUMERICAL DETAIL

3.1 Numerical procedure

In general, an approximate solution ofw(ξ,η) is easily obtained with the so-called regularization approach (called CVA in this paper) to smear away the discontinuity between laminar flow and plug flow regions as suggested by Papanastasiou [7]. Using the yield stressyτas the criterion, the whole cross section is divided into the yielded and unyielded regions. Using this continuous flow field as the initial guess, the governing equation (20) is solved, while Eq. (28)solved on the plug flow region. The boundary between two regions should be adjusted to approach gradually the state with the boundary conditions, Eqs. (22) and(31), simultaneously satisfied. All these procedures will be carried out in an iterative loop until the convergence.

There are some more check-ups on the integrity of the converged flow field. First is the force balance on each unyielded region (BorCin Fig. 2):

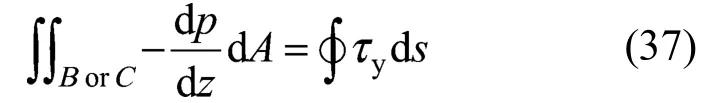
and the second is the total force balance over the cross section:

These may be used as the tests for numerical grid-independency. In above equations, the left hand side line integral is conducted along the boundary of respective cross section.

3.2 Grid independence

To validate the present in-house computer code, a case of fully developed laminar flow of 1.85% bentonite dispersion in 100% eccentric annulus [16] is simulated.The dispersion is well described with the Herschel-Bulkley model and the fitted constitutive equation is

The geometrical parameters of the annulus areR1=20 mm,R2=35 mm, and the eccentricitye=1.

Based on previous experience [14, 15], the gridindependence for similar numerical simulations was achieved on a 41×81 grid (denoting node numbers inξandηdirections). The orthogonal grid generated is plotted in Fig. 6. The maximum non-orthogonality is 0.087,and the average is 0.0046, just a little worse than the results reported in Section 2.5. Also to be noticed that this poor orthogonality occurs very near the touching walls, and it is expected to exert little effect on the fluid flow of other part of cross section with large flow velocity.

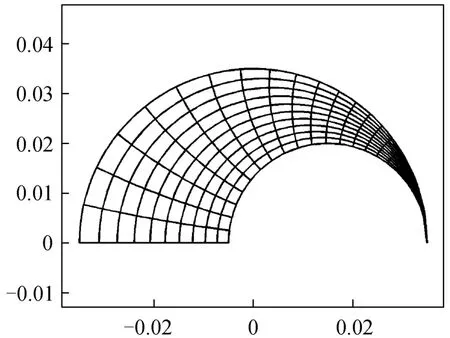
Figure 6 Boundary-fitted orthogonal coordinate system for e=1, R1=20 mm, R2=35 mm

The convergence criterion when the regularization approach (CVA) adopted is that the dimensionless relative residual of the algebraic equation sets forwdropped below 10-4.

4 SOLUTION BY CONTINUOUS VISCOPLASTIC APPROXIMATION

4.1 Numerical realization

As proposed by and practiced by many others,the continuous viscoplastic approximation (CVA) is rather simple for implementing the numerical simulation of flow of Herschel-Bulkley fluids. In this way,there is no plug flow region in the annulus and fluid flows everywhere, no matter how small the velocity is.By this approximation, regionBin Fig. 2 becomes that with low shear (＜τy), high apparent viscosity and almost flat velocity profile, while in regionCthe velocity would be very low, being almost stagnant. Only one governing equation is applicable: Eq. (10) for the flowing region. The discretized algebraic equation (19)simplifies to

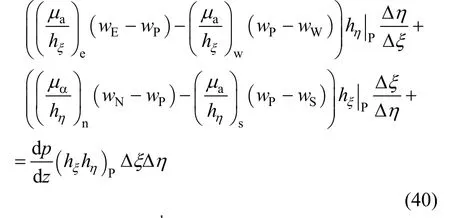
after the termKγn-1in Eq. (19) is replaced by the apparent viscosityμadefined in Eq. (4). The subsequent numerical simulation is quite routinely performed as dealing with other laminar viscous flow. It is noticed that for the present case of flow in the annulus, the value ofλis not very critical, andλ＞5.0 is sufficient to guarantee the numerical results being independent ofλ.

Kelessidiset al. [16] experimented on the flow of bentonite suspension as a drilling fluid through concentric and eccentric annuli in laminar and turbulent regimes. Here only the 6 cases of low pressure drop are simulated. The typical contour maps of velocity componentwand shear stressτare presented for the case of dp/dz=219.7 Pa·m-1,e=1.0 (fully eccentric),R2=35 mm,R1=20 mm in Fig. 7.

Figure 7 Contour maps in fully eccentric annulus with CVA (dp/dz=219.7 Pa·m-1, e=1.0, R2=35 mm, R1=20 mm)

On the first glance, the velocity contours are reasonable in Fig. 7 (a): the maximum velocity is at the wide side of the annulus. The shear stress is high at the walls on the wide side and it decreases in magnitude as it moves to the center of the annulus in Fig. 7(b); at the narrow side where the two walls touch, the velocity is very low, so does the shear stress. The blank band in the central annulus is the region bounded by the contour lines with the shear stress equal to the yield stressτy, and that may be presumed to be the approximate unyielded plug flow region. All these make sense only in the context of CVA approximation:such a plug flow region would flow in the wide side but adhere to the wall at the narrow side. This is an impossible flow pattern contradicting to the nature of yield viscoplastic fluids. It is considered that the CVA is conceptually inapplicable, and whether it is available for rough estimation of flow of Herschel-Bulkley fluids in annuli should be checked up with a good stock of experimental data.

Figure 8 Contour maps in fully eccentric annulus with CVA (dp/dz=414.2 Pa·m-1)

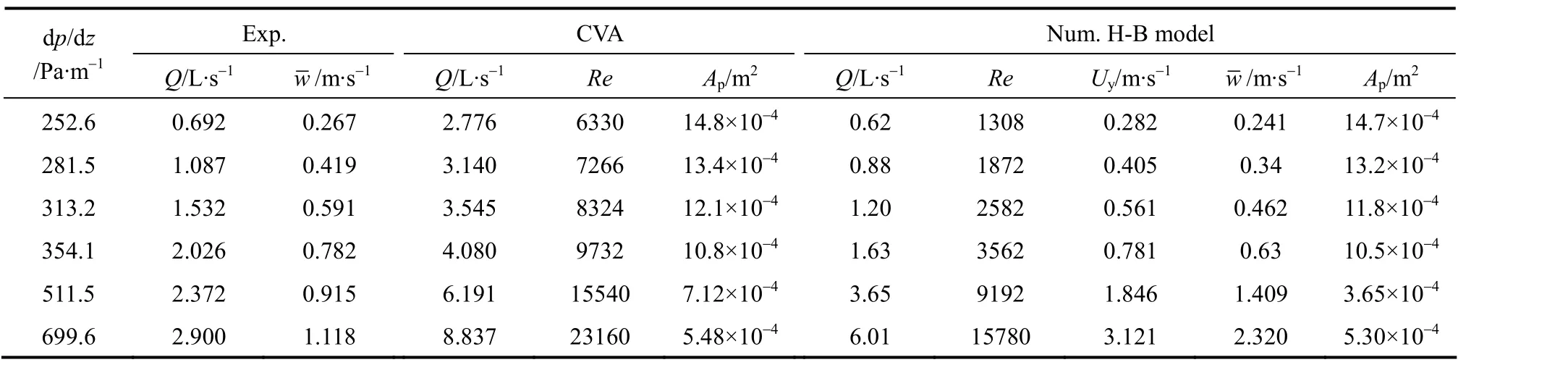
Table 1 Comparison of CVA simulation with experiment on concentric annulus [16]

Figure 8 presents a similar case of dp/dz=414.2 Pa·m-1, but Fig. 8 (b) indicates that the unyielded region is split into two, possibly the large one is the plug flow region amongst the shear flowing fluid and the small one by the narrow side is a stagnant block since it borders to the touching walls. The shapes of these two regions are very doubtful, and whether they satisfy the laws of elastic deformation in solid mechanics and the boundary condition (31) needs quantitative check-up.

4.2 Comparison with experimental data

Flow in concentric annulus is more easily simulated numerically since the grid suitable for this case is actually a polar coordinate system and the numerical generation of orthogonal grid is not necessary. The volumetric flow rate as calculated from the numerical solution of flow field is compared with the experimental data of low pressure drop by Kelessidiset al.[16] as listed in Tables 1 and 2.

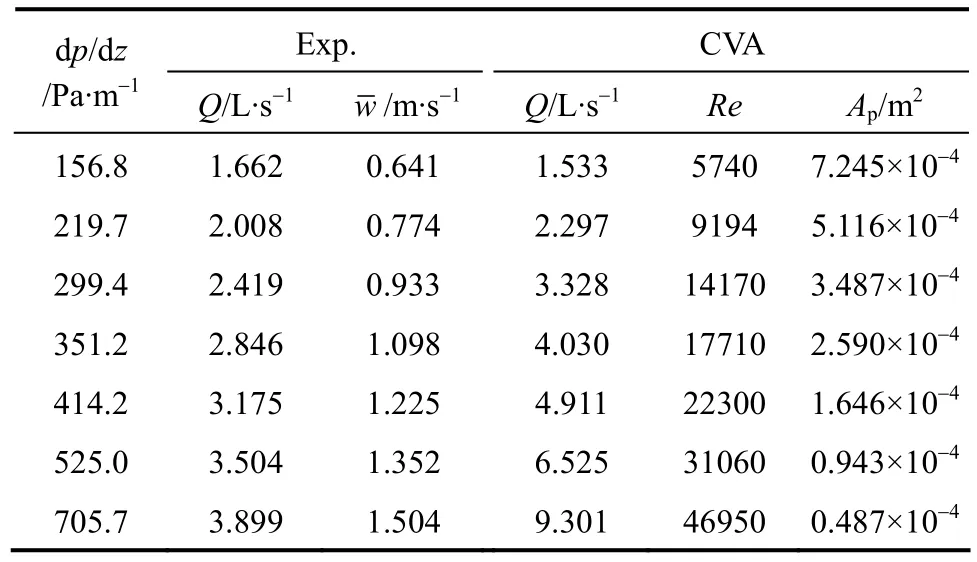
Table 2 Comparison of CVA simulation with experiments on eccentric annulus [16]

It seems that under the possibly laminar flow condition, the numerically predicted flow rates by the CVA approach are 1.8 times higher than the experimental measurements (statistics for first 4 rows of laminar flow in Table 1), although they follow roughly the same trend. The overestimation in eccentric annulus is less significant (only average relative error of 25% for 4 data with dp/dz＜400 Pa·m-1), possibly related with the more dramatic contrast among the local values of shear rate over the whole cross section.

In contrast, Kelessidiset al. [14] developed a unified approach to predict the relationship between the flow rate and pressure drop covering the whole range from laminar to fully turbulent flows in concentric annulus using analytical solution based on slit flow solution for laminar flow and a semi-empirical approach for turbulent and transitional flows with much less error than that from the CVA simulation. This suggests that the numerical simulation of Herschel-Bulkley fluids should be based on a better and more accurate model rather than simple CVA.

5 SPECIAL CASES OF RIGOROUS SOLUTION

5.1 Strategy for concentric annulus

For the non-Newtonian fluid flow in annulus, the present set of governing partial differential equation consists of Eq. (12) for velocity componentwand Eq.(28) for elastic deformationb.

The boundary condition forwis thatw=0 at solid wall, andwat the boundary between the flow region and the unyielded region is a constant to be determined in the solution. The boundary condition forbis Eq. (31)which implies the elastic stress at the boundary of unyielded region equals exactly to the yield stressτy.

It is desired to solve the above mathematical problem by an iterative numerical procedure to get the steady flow field, which needs to adjust the boundary position and the plug velocity iteratively. From the authors’ efforts, it seems the task to get a converged solution is very difficult. In this work we turn to some simple cases, namely, we presume the possible and rational flow structure and solve quantitatively for the flow field belong to this flow pattern.

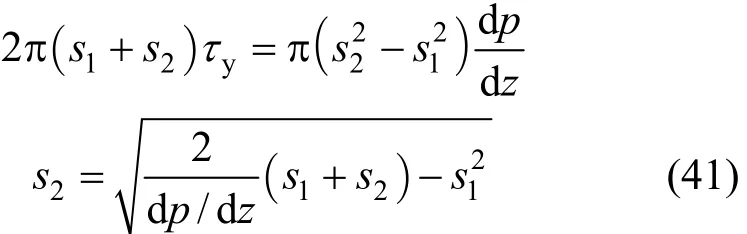
Figure 9 Flow structure in a concentric annulus with a plug flow regionA—shear flow region (0γ＞); B—unyielded region (plug flow)(0γ=)

We have foreseen a typical flow structure in a concentric annulus as illustrated in Fig. 9. Because of the axial symmetry, the plug flow region is also an annular ring demarcated by radiis1ands2. The force balance over this region, Eq. (37), dictates the pressure drop be balanced by the yield stress at the boundary circles:So eithers1ors2is to be resolved when the pressure drop is specified in advance. Another undetermined parameter is the linear velocity of the plug flow regionwy. We select the correct values ofs1andwyto satisfy the partial differential equations (PDEs) and the required boundary conditions. This can be easily accomplished using common optimization techniques to search over a two-dimensional parameter domain fors1andwy. The optimization algorithm adopted here is a simple and robust one: the complex method.

The numerically predicted results of flow rate in the vigorous Herschel-Bulkley model for the concentric annulus are listed in last columns of Table 1. It is easy to find that the rigorous prediction is more close to the experimental measurements than the CVA simulation. For the first 4 data with low Reynolds number as defined by where the hydraulic diameter 2(R2-R1) of annulus is used andμavis the area-weighted average of apparent viscosity defined by Eq. (4), the rigorous simulation predictsQwith the average relative error of -17.7%only. The residuals for PDEs are quite small, and the boundary condition of velocity gradient equaling to

zero for the shear flow region is enforced quite well.For the case of dp/dz=354.1 Pa·m-1, the average velocity gradient along the two boundaries of the plug flow region is 4.98×10-7s-1and the corresponding standard deviation is 1.4×10-4in contrast to the reference value of 2wy/(R2-R1)=104.1 s-1. Boundary condition (31) forbis also well enforced: the bias of

/bn?? fromτy/G=1.073 is only 2.67×10-7on the average with a standard deviation of 1.368×10-4. Fig.11 plots the elastic deformationbversusthe radial coordinate, giving a smooth curve satisfying the Poison equation (28) thatb(r) observes, in good accordance with the general picture depicted in Fig. 3. It is nice to see that the curve at the both ends is smoothly connected with the main domain of plug flow region,for the main part of the curve are computed based on complete cells while the ending value ofbis dependent on the boundary condition and computed based on incomplete cells. The simulated results in Table 1 and Figs. 10 and 11 suggest strongly that the present results from the rigorous models are reliable and convincing.

For laminar flow of Herschel-Bulkley fluid in concentric annulus, many authors presented analytic solution, typically as developed by Hanks [17]. The numerical values of the volumetric flow rate under low pressure drops in Table 1 as calculated by Hanks’solution are compared with the experimental data by Kelessidiset al. [16] and the predicted by the strict model in Fig. 12. It is observed that the strict model prediction is pretty close to experimental data and analytical solution, particularly when dp/dz＜400 Pa·m-1and the flow is possibly laminar (Re＜3562).This also offers supporting evidence to the soundness of the strict mathematical model proposed in this work.In contrast, the CVA approach seems not to be reliable.

By the way, Eq. (38) was used as a check of the soundness of the numerical simulation in this section,the total wall shear is only about -3.5% lower than the produce of applied pressure drop by the cross-sectional area for the 6 cases of concentric annular flow in Table 1, which is slightly larger than the average of-2.4% for the CVA results. However, it is expected the error would decrease further when finer grids are adopted for simulation.

Figure 10 Shear stress in shear flow region and plug region deformation in concentric annulus with a plug flow region(dp/dz=354.1 Pa·m-1, G=1, τy=1.073 Pa)

Figure 11 Elastic deformation across the plug flow region in concentric annulus (dp/dz=354.1 Pa·m-1, G=1, τy=1.073 Pa)

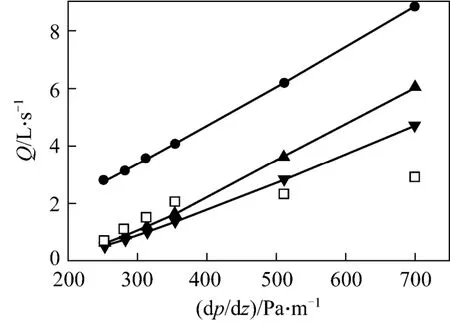
Figure 12 Comparison of the prediction by the strict model with experimental data and analytic solution (Concentric annulus, R2=0.035 m, R1=0.020 m)□ exp.; ● CVA; ▲ strict model; ▼ analytic

Figure 13 Possible flow structures in an eccentric annulus with flowing and stagnant plug regionsA—shear flow region (0γ＞); B—unyielded flow region (plug flow) (0γ=); C—unyielded stagnant region (dead zone) (0γ=)

5.2 Strategy for eccentric annulus

Since a plug flow region as presumed in Fig. 7 (b)is not likely, another possible configuration is presumed in Fig. 13 (a), in which a plug flow region in motion is isolated from tube walls and a stagnant plug region sticks to the touching walls, in somewhat resemblance to the structure in Fig. 8 (b). The flowing plug flow is also driven by the same constant pressure drop as the shearing flow, therefore the force balance on this region must be observed. From the knowledge on elastic deformation of solid body, the plug flow region must be circular, leading to the following force balance:

which dictates the circular plug floe region has a radius of

This condition would exclude geometrically the existence of a stable plug flow region when the wide side gap of the annulus is small (R2-R1＜Ry).

For the configuration in Fig. 13 (a), two parameters, the location of plug flow region centerS1and the plug velocity, specifies the status of a Herschel-Bulkley fluid of the flowing plug, when the annular geometry and pressure drop are specified, but the formulation and specification of the stagnant plug region are still pending. Besides, many flow structures are feasible,for example, the structure in Fig. 13 (b) may not be stable but could exist when flow structure transition is occurring.

Many authors explored the flow structure of Bingham plastic fluids in different ducts [8]. Walton and Bittleston [18] argued the existence of three regions in an eccentric annulus: true plug, pseudo-plug and shearing flow regions as sketched in Fig. 13 (c) and the shape of true plug flow region as sketched therein was accepted by some latter authors (for example [19]).The meaning of a pseudo-plug seems somewhat ambiguous. In our perception, the general structure like Fig. 13 (d) with shear flow region A, plug flow region B and stagnant region C seems more reasonable, and the relevant justification is presently under way.

Numerical solution in eccentric annuli may proceed based on the strict model, either with an iterative algorithm or by an optimization procedure.

5.3 Problems to be resolved

From the above exploration, it is certain that the rigorous numerical simulation of yield viscoplastic fluids based on the Herschel-Bukcley model is necessary, because the predictability of CVA is found to be rather poor. There are at least three problems to be tackled before the non-Newtonian flow of Herschel-Bulkley fluids can be numerically simulated with sufficient accuracy.

Firstly, a robust iterative algorithm has to be developed to solve conjugatedly the shearing flow in yielded flow region and the plug flow with elastic deformation amid the flowing Herschel-Bulkley fluids,so that the physical constraints on the boundary between these two regions can be satisfied. Simple empirical way of linear addition of corrections for the deviation of velocity gradient from zero at the side of shearing flow region and the bias of elastic deformation stress from yield stress at the side of plug flow region seems not working for our case of rigorous simulation. A more accurate mechanism-based equation for estimating the correction to the boundary location is more desired.

Secondly, it is demonstrated by numerical solution that a stable flow structure as in Fig. 9 exists in accordance to the governing equations subject to necessary boundary conditions. However, it is difficult to image that a ring-shaped plug flow region remains mechanically stable as its width reduces to a small value.It might break into small round pieces of plug flow. It is necessary to resolve the process of breakage on a dynamics based numerical scheme. To describe such a process, the mathematical model of the steady-state fully developed axial flow needs to be extended to suit the more complicated time-dependent flow. Thus, the dynamic nature of fluid flow and flow patter transition must be studied on the time-dependent basis.

Thirdly, the experimental validation of numerical prediction also awaits technical improvements. The flow rate-pressure drop data are not revealing enough to distinguish the mesoscopic difference among diversified models. The experimental data on dimension and shape of the plug flow region in annuli have not been reported. The measurement and visualization techniques seem to need further development, particularly for opaque or turbid non-Newtonian fluids, to provide the provisions to answer whether the plug flow region maintains its identity or not when being mechanically or turbulently perturbed, whether the multiple stable flow structures exist, and how the transition of flow structure occurs and develops.

6 CONCLUSIONS

Mathematical model of a yield viscoplastic fluid flowing through concentric and eccentric annuli is established and the algorithm based on a finite difference method over the boundary-fitted orthogonal coordinate system is developed. The present preliminary work on numerical simulation may be concluded as follows:

(1) Strict mathematical formulation of the flow of Herschel-Bulkley fluids is established, in which the shear flow region is governed by momentum conservation in combination with the constitutive equation of the Herschel-Bulkley fluid, and the plug flow region is controlled by the law of elastic solid mechanics of the unyielded region of Herschel-Bulkley fluid. The constraint conditions at the boundary between two regions are formulated. These equations constitute a well-posed mathematical problem for numerical solution.

(2) The problem can be simplified greatly by adopting the continuous viscoplastic approximation(CVA) to bypass the discontinuity of shear stress at zero rate of strain. But this approach to the Herschel-Bulkley fluid flow is found to overestimate greatly the volumetric flow rate of a bentonite suspension in a concentric annulus as compared with the experimental data. However, the overestimation for an eccentric annulus decreases to reasonable level for dp/dz＜400 Pa·m-1. Besides, the region of plug flow demarcated byyττ= in eccentric annulus is problematic as judged from the nature of Herschel-Bulkley fluids, and it could not exist in practice. Hence, CVA gives only the qualitative trend of the flow rate versus pressure drop, not the flow structure in detail.

(3) A strict numerical procedure based on the Herschel-Bulkley model is proposed, but its numerical implementation by iterative adjustment of the boundary location and the plug flow velocity fails despite serious efforts devoted, especially for eccentric annuli.A robust algorithm needs to be developed to get the converged solution of the general Herschel-Bulkley fluid flow with reasonable accuracy.

(4) With the solid mechanics analysis of the plug flow region, some possible flow structures are presumed for their shape and location in annuli, and the flow under these structures can be resolved by numerical optimization of the parameters specifying such a structure. Only the case of flow of Herschel-Bulkley fluid in a concentric annulus is thus resolved and the predicted flow rate is in much better accordance to the experimental data than CVA simulation. However, the solution by optimization in an eccentric annulus remains to be a challenge, and more thorough analysis of the flow structure is necessary.

NOMENCLATURE

AParea of plug flow region, m2

b elastic deformation, m

e eccentricity

f (ξ, η) distortion function

G elasticity modulus of unyielded fluid, Pa·m-1

hξ, hηscaling factor, m

i unit vector

K fluid consistency

n fluid behavior index

dp/dz pressure drop, Pa·m-1

Q flow rate, L·s-1

Re Reynolds number, 2U(R2-R1)ρ/μav

R1inner radius of annulus, m

R2outer radius of annulus, m

s1, s2inner and outer radii of plug flow region, m

U average velocity, m·s-1

w axial velocity component, m·s-1

wyvelocity of unyielded fluid (plug), m·s-1

x, y coordinates in physical plane, m

α, β numerical constant

γ shear rate, s-1

θ orientation angle of gradient

λ constant defined in Eq. (4)

μ viscosity, Pa·s

ξ, η coordinate in computational plane, 0≤ξ, η≤1

ρ density, kg·m-3

τ stress tensor component, Pa

τyyield stress, Pa

Subscripts

y yield stress

z axial coordinate

1 Bird, S.R., Stewart, W.B., Lightfoot, B.N., Transport Phenomena,New York, Wiley (1960).

2 Chhabra, R.P., Bubbles, Drops, and Particles in Non-Newtonian Fluids, 2nd edition, Taylor Francis (2007).

3 Kelessidis, V.C., Maglione, R., Tsamantaki, C., Aspirtakis, Y., “Optimal determination of rheological parameters for Herschel-Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling”, J. Petrol. Sci. Eng., 53, 203-224(2006).

4 Kelessidis, V.C., Maglione, R., “Yield stress of water-bentonite dispersions”, Colloids Surfaces A Physicochem. Eng. Aspects, 318 (1-3),217-226 (2008).

5 Glowinski, R., Wachs, A., “On the numerical simulation of viscoplastic fluid flow”, In: Handbook of Numerical Analysis, Vol. 16,Numerical Methods for Non-Newtonian Fluids, Glowinski, R., Xu,J., eds., North-Holland, Amsterdam, 483-717 (2011).

6 Dean, E.J., Glowinski, R., Guidoboni, G., “On the numerical simulation of Bingham visco-plastic flow: Old and new results”, J.Non-Newt. Fluid Mech., 142, 36-62 (2007).

7 Papanastasiou, T.C., “Flows of materials with yield”, J. Rheol., 31,385-404 (1987).

8 Papanastasiou, T.C., Boudouvis, A.G., “Flows of viscoplastic materials:Models and computations”, Comput. Struct., 64, 677-694 (1997).

9 Hussain, Q.E., Sharif, M.A.R., “Numerical modeling of helical flow of viscoplastic fluids in eccentric annuli”, AIChE J., 46 (10),1937-1946 (2000).

10 Beverly, C.R., Tanner, R. I., “Numerical analysis of three-dimensional Bingham plastic flow”, J. Non-Newt. Fluid Mech., 42, 85-115 (1992).

11 Vradis, G.C., Dougher, J., Kumar, S., “Entrance pipe flow and heat transfer for a Bingham plastic”, Int. J. Heat Mass Transfer, 36,543-552 (1993).

12 Patankar, S.V., Numerical Heat Transfer and Fluid Flow, McGraw-Hill,New York (1980).

13 Ryskin, G., Leal, L.G., “Orthogonal mapping”, J. Comput. Phys., 50,71-100 (1983).

14 Mao, Z.S., “Numerical simulation of viscous flow through spherical particle assemblage with the modified cell model”, Chin. J. Chem.Eng., 10, 149-162 (2002).

15 Mao, Z.S., Wang, Y.F., “Numerical simulation of mass transfer in a spherical particle assemblage with the cell model”, Powder Technol.,134, 145-155 (2003).

16 Kelessidis, V.C., Dalamarinis, P., Maglione, R., “Experimental study and predictions of pressure losses of fluids modeled as Herschel-Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows”, J. Petrol. Sci. Eng., 77, 305-312 (2011).

17 Hanks, R.W., “The axial flow of yield-pseudoplastic fluids in a concentric annulus”, Ind. Eng. Chem. Process Des. Dev., 18, 488-493(1979).

18 Walton, I.C., Bittleston, S.H., “The axial flow of a Bingham plastic in a narrow eccentric annulus”, J. Fluid Mech., 222, 39-60 (1991).

19 Meuric, O.F.J., Wakeman, R.J., Chiu, T.W., Fisher, K., “Numerical flow simulation of viscoplastic fluids in annuli”, Can. J. Chem. Eng,76, 27-40 (1998).