PKP-方程的精確周期孤子解和雙周期解

李自田

PKP-方程的精確周期孤子解和雙周期解

李自田

(曲靖師范學(xué)院數(shù)學(xué)與信息科學(xué)學(xué)院,云南曲靖655011)

應(yīng)用同宿測(cè)試方法研究并獲得了PKP-方程的新的精確周期孤子解和雙周期解,同時(shí)得出了該方程在點(diǎn)p2=4處具有衰減性.從平衡點(diǎn)的左側(cè)到右側(cè),方程的解從周期孤子解衰變?yōu)殡p周期解.

周期孤子解;雙周期;同宿測(cè)試法;衰減

0 引言

在過去的二十年里,在非線性發(fā)展方程廣泛出現(xiàn)的應(yīng)用領(lǐng)域引起了數(shù)學(xué)和物理工作者的普遍關(guān)注,許多學(xué)者在這一領(lǐng)域進(jìn)行了卓有成效的研究.特別是在精確解的尋求和獲得方面開辟和發(fā)展了許多方法.諸如, F-擴(kuò)展法[1];齊次平衡法[2]以及逆散射法[3]等.

在本文中,我們將研究如下形式的PKP-方程:其中u:Rx×Ry×Rt→R.并且:取自“+”和“-”被分別稱為PKP-I方程和PKP-II方程.

眾所周知,該模型屬于潘勒衛(wèi)不可積類型.但通過應(yīng)用潘勒衛(wèi)擴(kuò)展變換,我們可將該方程轉(zhuǎn)換為雙線性方程,進(jìn)而通過對(duì)雙線性方程的研究,可找出并獲得該方程的解.

最近以來(lái),該方程在諸多方面獲得了較廣泛的研究[3-6].許多學(xué)者在這些方面取得了很大的進(jìn)展.文獻(xiàn)[5]通過應(yīng)用F-擴(kuò)展函數(shù)的方法研究并獲得了用橢圓函數(shù)表示的一系列周期波解;在文獻(xiàn)[6]中,文章的作者給出了該系統(tǒng)的N-孤子解,并得出了該系統(tǒng)可簡(jiǎn)化為Melnikov-方程和KP-方程的特殊類型的結(jié)論.

本文通過對(duì)雙線形方程的研究,應(yīng)用文獻(xiàn)[7]發(fā)展起來(lái)的方法,即同宿測(cè)試法,獲得了該方程的新的周期解和雙孤子解,其中的一些方法的應(yīng)用和結(jié)論在解決其他同類型的問題中將具有十分深遠(yuǎn)的意義.

1 PKP-I方程的解

首先,我們考慮PKP-I方程:

引入變換:

將(3)代入方程(2),則方程(2)可化為:

隨后,我們采用下面的變換:

將變換(5)代入方程(4),則我們得到如下形式的雙線性方程:

這里,算子“D”定義為:

引入測(cè)試函數(shù):

其中b1,b2,Ω,τ,p是實(shí)數(shù).

將(7)式代入方程(6),通過計(jì)算,我們得到如下的關(guān)系式:

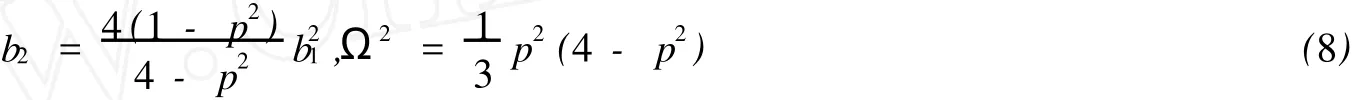
從而,將(8)代入(7)并代入(5),我們得到方程的周期孤子解:

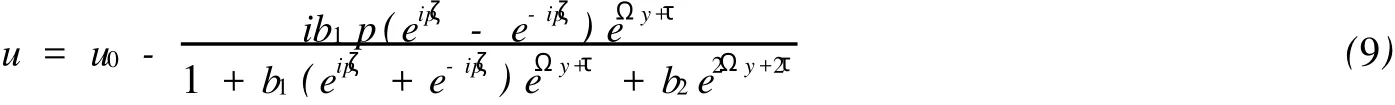
顯然,我們要求條件:

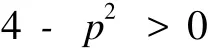
以便使式(8)中的Ω2>0,從而確保Ω能取到實(shí)數(shù).

把ζ=x+t代入(9)中,并令b2=1.從而,我們得到下列形式的周期孤子解:

2 PKP-II方程的解

考察如下形式的PKP-II方程:

應(yīng)用和上面使用的相同的變換以及處理PKP-I方程所用的類似的方法,我們有雙線性方程:

設(shè):

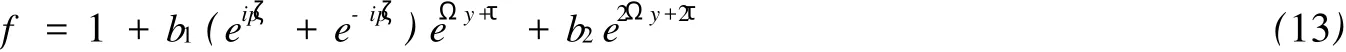
將(13)代入方程(12)并應(yīng)用符號(hào)計(jì)算系統(tǒng),我們獲得了方程(11)的精確解:

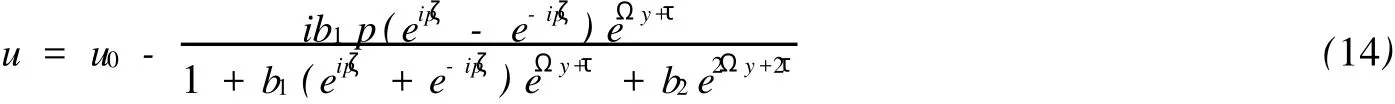
其中系數(shù)滿足:

同理,要求條件:p2>4,從而使得(15)中Ω的滿足Ω2>0.

類似地,我們?nèi)2=1.則PKP-II方程的精確解具有如下表達(dá)式:

3 解的研究

考慮變換:(ζ,y)→(ζ,iy)

將它代入(9)并令τ=0.我們得到了一個(gè)新解,它是一個(gè)雙周期解:

比較方程(2)和方程(11),我們不難發(fā)現(xiàn),只要我們應(yīng)用時(shí)間和空間的變換(ζ,y)→(ζ,iy),方程(2)可以轉(zhuǎn)換為方程(11),反之亦然.這樣,我們獲得了PKP-I方程的雙周期解:

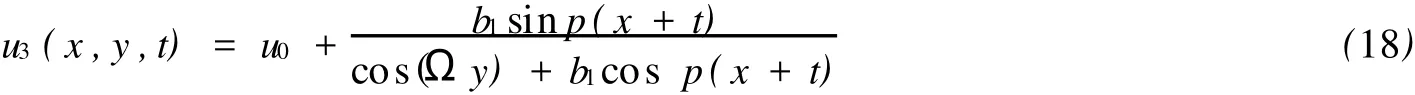
其中:p2-4>0.

注意到,(18)是PKP-I方程的奇性周期解.為了避免奇性,我們令cos(Ωy)>0和cosp(x+t)>0.

此外,同理可得PKP-II方程的雙周期解:

其中,要求條件:p2-4<0.

依據(jù)討論,我們得出結(jié)論:p2=4是PKP-I方程和PKP-II方程的唯一周期分歧點(diǎn).在p2=4的兩側(cè), PKP-I方程和PKP-II方程的解的性質(zhì)發(fā)生了改變.當(dāng)平衡點(diǎn)p2從4的一側(cè)變到另一側(cè),周期孤子解衰變?yōu)殡p周期解.

[1] ZHANG Hui-qun.New Exact Travelling Wave Solutions for Some Nonlinear Evolution Equations,Part II[J].Chaos, Solitons and Fractals,2008,37:1328-1334.

[2] ZHOU Yu-bin,WNAG Ming-liang,MIAO Tian-de.The Periodic Wave Solutions and Solitary Wave Solutions for a Class of Nonlinear Partial Differential Equations[J].Phys Lett A,2004,323(1-2):77-88.

[3] ABLOWITZ M J,CLARKSON P A.Solitons,Nonlinear Evolution Equations and Inverse Scattering Transform[M]. Cambridge University Press,1990:8-17

[4] CARIELLO F,TABOR M.Painleve Expansions for Non-integrable Evolution Equations[J].Physica D:Nonlinear Phenomena,1989,39(1):77-94.

[5] AKHMEDIEV N,ANKIEWICZ A.Solitons,Nonlinear Pulses and Beams[M].Chapman and Hall,London,1997:124-127.

[6] ZHOU Yu-bin,WANG Ming-liang.Periodic Wave Solutions to a Coupled Kdv Equations with Variable Coefficients[J]. Phys Lett A,2003,308(1):31-36.

[7] DAI Zheng-de,LI Shao-ling,ZHU Ai-jun.Singular Periodic Soliton Solutions and Resonance for the Kadomtsev-Petviashvili Equation[J].Chaos,Solitons and Fractals,2007,34(4):1148.

Exact Periodic Soliton Solution and Double Periodic Solution to PKP-equations

LI Zi-tian
(College of Mathematics and Inf ormation Science,Qujing Normal University,Qujing655011,China)

The periodic soliton and the double periodic solutions to PKP-equation are obtained by using homoclinic test method.Mean while,we also find that the equation has the properties of degeneration atp2= 4.When the equilibriumpvaries from one side ofp2=4 to the other side,the periodic soliton solution changes into a doubly periodic solution.

periodic soliton solutions;double periodic;homoclinic test method;degeneration

O175.23

A

0253-2395(2010)02-0166-03

2009-04-07

國(guó)家自然科學(xué)基金(10361007,10661002);云南省教育廳科學(xué)研究基金項(xiàng)目(08Y0302);曲靖師范學(xué)院科研基金(2008MS018;2009MS007)

李自田(1972-),男,碩士,講師,主要從事偏微分方程研究.E-mail:lizitian88@163.com