A LEAST SQUARE BASED WEAK GALERKIN FINITE ELEMENT METHOD FOR SECOND ORDER ELLIPTIC EQUATIONS IN NON-DIVERGENCE FORM?

Peng ZHU (祝鵬)?

College of Mathematics, Physics and Information Engineering, Jiaxing University,Jiaxing 314001, China

E-mail : zhupeng.hnu@gmail.com

Xiaoshen WANG (王筱沈)

Department of Mathematics and Statistics, University of Arkansas at Little Rock,Little Rock, AR 72204, USA

E-mail : xxwang@ualr.edu

where the coefficient tensor A(x)={aij(x)}d×dis assumed to be symmetric,uniformly bounded and positive definite. Hereis the Hessian matrix of u, and A : D2u =

Elliptic problems in non-divergence form have applications in stochastic processes and game theory. The problems can not be rewritten in divergence form when coefficients aijare nonsmooth. The non-divergence form of (1.1) makes it almost impossible to have a weak formulation, and thus it is difficult to derive and analyze the finite element methods for solving this PDE.To overcome this difficulty, quite a few papers have been devoted in recent years to finite element methods for solving this equation using various special kinds of treatments (e.g. [1–3, 6, 8, 11]). The least square method is a general method which can be used to find the best approximation of a given function from a vector space with respect to a certain inner product.Thus, the resulting linear system is always symmetric and positive definite.

Among the references mentioned above, [8]has the flavor of the least square method and[6, 8]are least square based methods. A least square formulation of this problem can be described as follows: let V be a finite dimensional vector space of functions defined on ? and

a least square solution of (1.1) is u ∈V, so that A : D2u is the L2orthogonal projection of f onto W, and thus

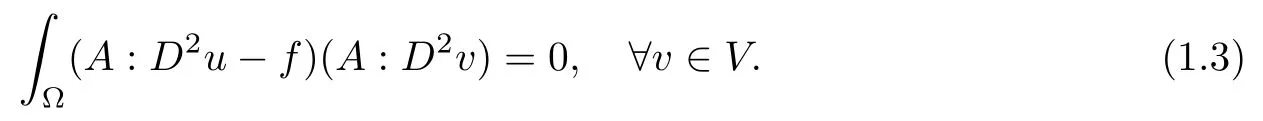
Taking advantage of these nice properties, in [6], the authors proposed a least square based simple DG finite element method for solving (1.1). Optimal convergence rate in an H2equivalent norm was proved, and an optimal convergence order of the H1norm and a suboptimal convergence order of L2norm were observed in numerical results. This paper will follow the ideas developed in [6]to establish a least square based weak Galerkin method for solving(1.3),where the Hessian is replaced by the discrete weak Hessian operator introduced in[11]. In order for the least square solutions to converge to the strong solution of (1.1), V is replaced by some finite element spaces Vh, where h →0 is the mesh size. In addition, a stabilizer is added to enforce the weak continuity. Naturally,the resulting linear system is symmetric,positive definite,and the algorithm is easy to implement and analyze. It is worth noting that the stabilizer used in our algorithms is different from the one used in [6], which leads to much better numerical results: an optimal convergence order in the L2norm and the superconvergent property in the H2equivalent normare observed.

To keep this article more focused on the new method itself, throughout the paper, we also assume that the coefficients aijare either continuous or satisfy the Cord`es condition[4]; that is,that there is ε ∈ (0,1) such that, for a.e. x ∈ ?,

Then, the problem (1.1) has a unique strong solution inwith the following a priori estimate:

For more details on the conditions which guarantee the existence and uniqueness of the solution of (1.1), we refer interested readers to [8]and the references therein.

The rest of the article is organized as follows: in Section 2, the least square based weak Galerkin method is introduced. The error estimates are given is Section 3. Numerical experiments are given in Section 4. Section 5 is devoted to some concluding remarks.

2 Least Square Based Weak Galerkin Method

Denote a finite element partition of the domain ? into polygons in 2D, or polyhedra in 3D, by Th. Let the set of all edges or flat faces in Thbe denoted by Eh, and?? the set of all interior edges or flat faces. Assume that Thsatisfies the shape regularity conditions described in[10]or[5]. Denote the diameter of K ∈Thby hKand the meshsize of the partition Th by h=maxK∈ThhK.

For a given integer k ≥2, let Vhbe the weak Galerkin finite element space associated with Thdefined as follows:

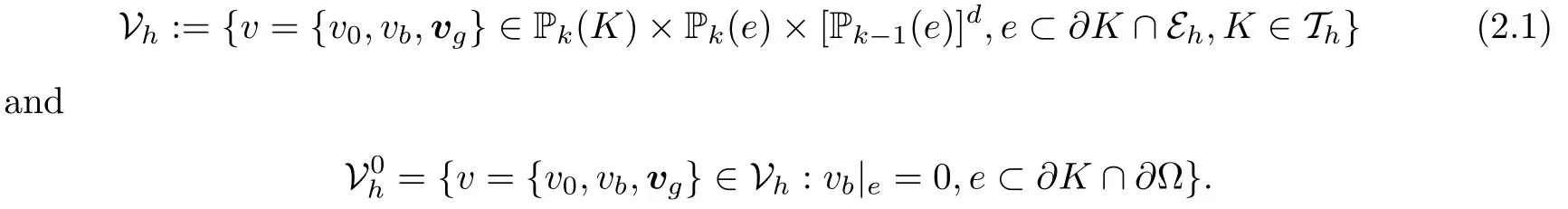
It should be pointed out that any function v = {v0,vb,vg} ∈Vhhas a single value vband vgon each edge e ∈Eh.

Definition 2.1(see[11]) For any v ={v0,vb,vg},a second order weak derivativePk?1(K) is defined on K as the unique polynomial satisfying

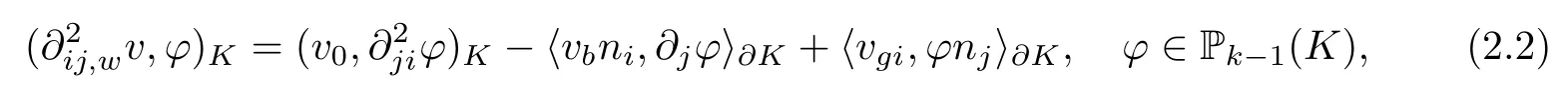
where n = (n1,··· ,nd) is the unit outward normal vector on ?K; its weak Hessian is defined element-wise by

We introduce a stabilization term

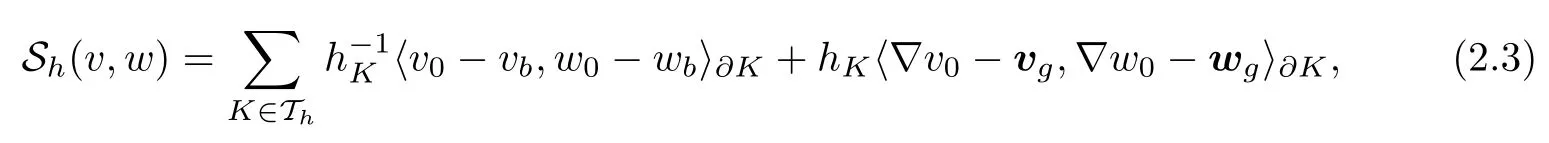
and a bilinear form

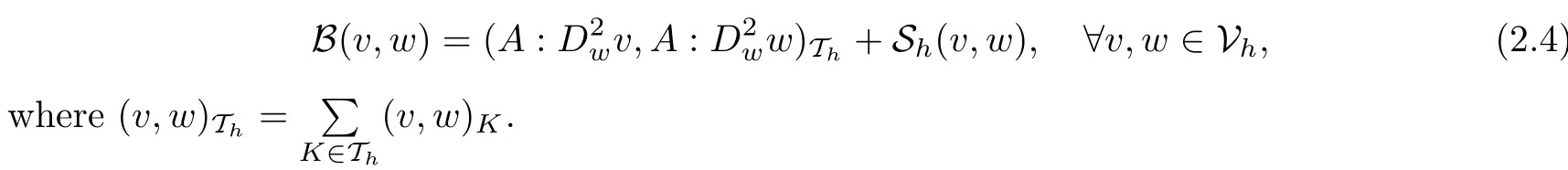
LS-WGMFor a numerical approximation of the solution of the second order elliptic problem (1.1) in the non-divergence form, we are seekingsuch that

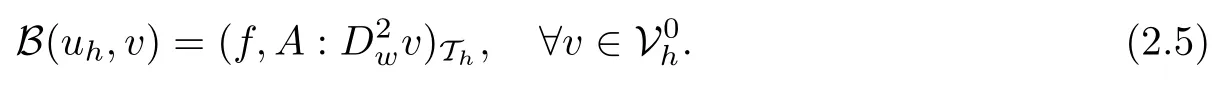
i.e., for v ={v0,vb,vg}∈Vh,

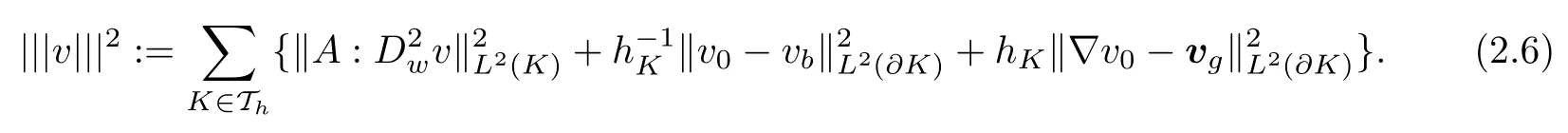
The following lemma shows thatis indeed a norm in the subspace

Lemma 2.2Assume that the coefficient tensor A(x) is symmetric, uniformly bounded and positive definite. Ifsatisfiesthen one must have v ≡ 0.

ProofAssume thatsatisfiesIt follows from (2.6) that

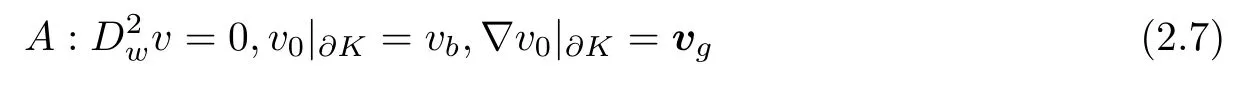
for all K ∈ Th. Thus,and satisfies

which implies that v0is a solution of the problem (1.1) with f = 0. It follows from the H2-regularity assumption (1.4) that v0=0. This completes the proof.

3 Error Estimate

In this section, we aim to estimate the error between the exact solution of problem (1.1)and its approximation from (2.5).

Firstly, we introduce some projection operators. For each element K, denote by Q0the L2projection onto Pk(K), k ≥ 2. For each edge or face e ? ?K, denote by Qband Qg=(Qg1,Qg2,··· ,Qgd) the L2projections onto Pk(e) and [Pk?1(e)]d, respectively. For any w ∈H2(?), denote by Qhw the L2projection onto the weak finite element space Vhsuch that on each element K, Qhw = {Q0w,Qbw,Qg(?w)}. Let Rhbe the L2projection defined elementwise onto Pk?1(K).

Lemma 3.1For any w ∈ H2(K),K ∈ Th, Qhand Rhsatisfy the following commutative property:

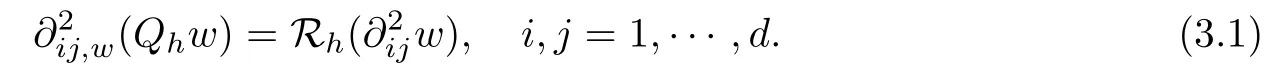
Denote the weak function {w|K,w|?K,(?w)|?K} by w. Then

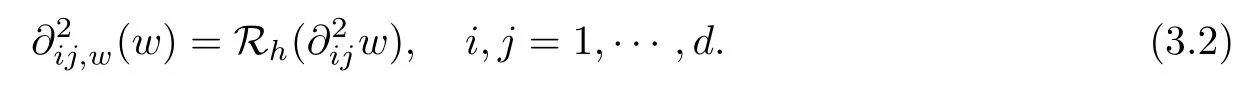
ProofFor any ? ∈ Pk?1(K) and i,j = 1,··· ,d, it follows from (2.2), the orthogonal properties of L2projections Q0, Qband Qgi, and integration by parts, that

which implies (3.1). The identity (3.2)can be proved in a fashion similar to (3.1). The proof is completed.

For any w ∈H2(Th), by Lemma 3.1 we have

The following trace inequality is useful in our error analysis: for any K ∈ Thand ? ∈H1(K), we have

The following estimates for the L2-projections will be used in the forthcoming error analysis:

Lemma 3.2(see [10]) Let Thbe a shape-regular finite element partition of the domain?. Then, for any 0 ≤ s ≤ 2 and 1 ≤ m ≤ k, it holds that

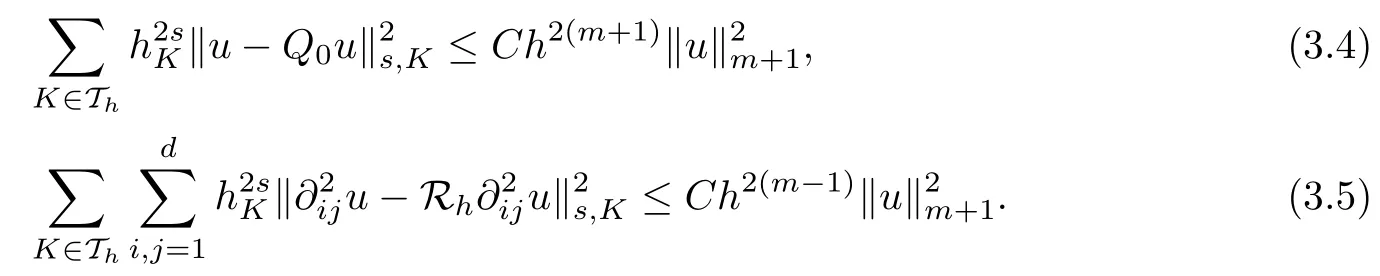
Lemma 3.3Assume that the coefficient tensor A(x) is uniformly bounded on ?. Then the error functions ehgiven by

satisfy the error equation

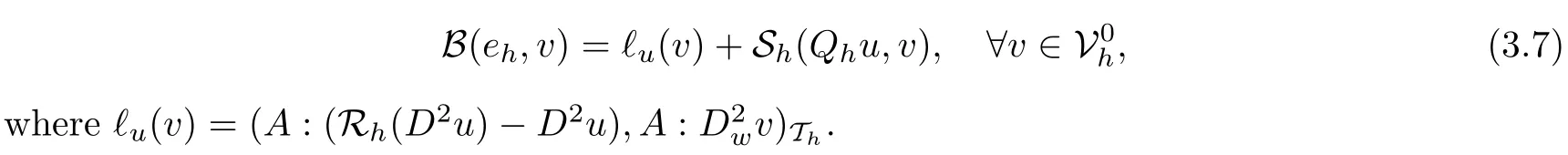
ProofLet v ∈be any test function. From (2.4) and Lemma 3.1, we have

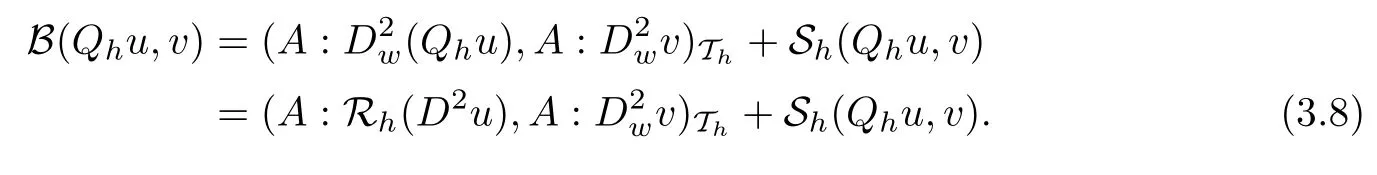
Substracting (2.5) from (3.8) implies that

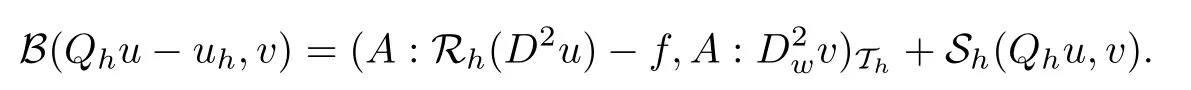
Plugging A:D2u=f into the above equation, we arrive at the conclusion (3.7).

Lemma 3.4Assume that This shape regular. Then for any w ∈ Hk+1(?) and v ∈ Vh,we have

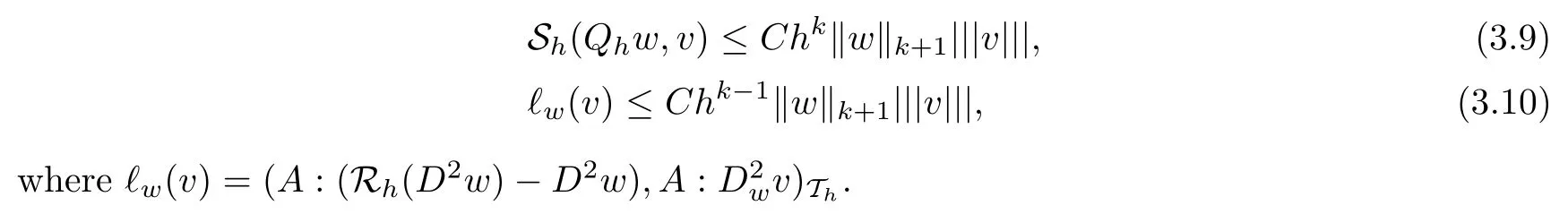
ProofBy the definition of SK(·,·) as defined in(2.3)and the properties of L2projection operators Qband Qg, we have

From trace inequality (3.3) and the estimate (3.4) with m=k, we obtain

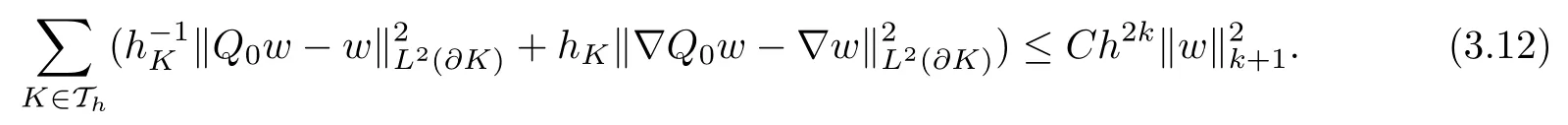
(3.9) follows from (3.11) and (3.12).

As for (3.10), it follows from the Cauchy-Schwartz inequality and the estimate (3.5) with m=k that

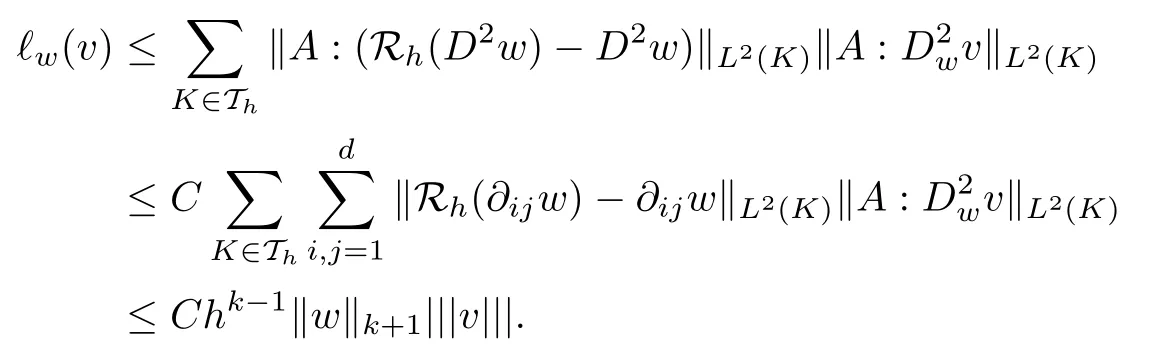
This completes the proof.

Theorem 3.5Assume that the coefficient tensor A(x) is uniformly bounded on ?. Let u ∈ Hk+1(?) be the solution of problem (1.1), and Qhu the L2projection of u onto the finite element spaceThen there exists a positive constant C such that

ProofIt follows from (2.6) that

It follows from Lemma 3.1 thatThen,we get that

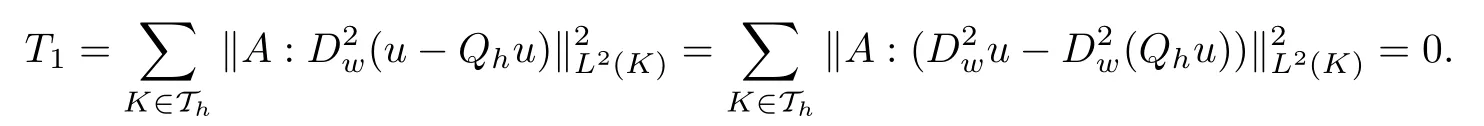
By the triangle inequality,the trace inequality(3.3)and Lemma 3.2,we obtain the upper bound of T2as follows:

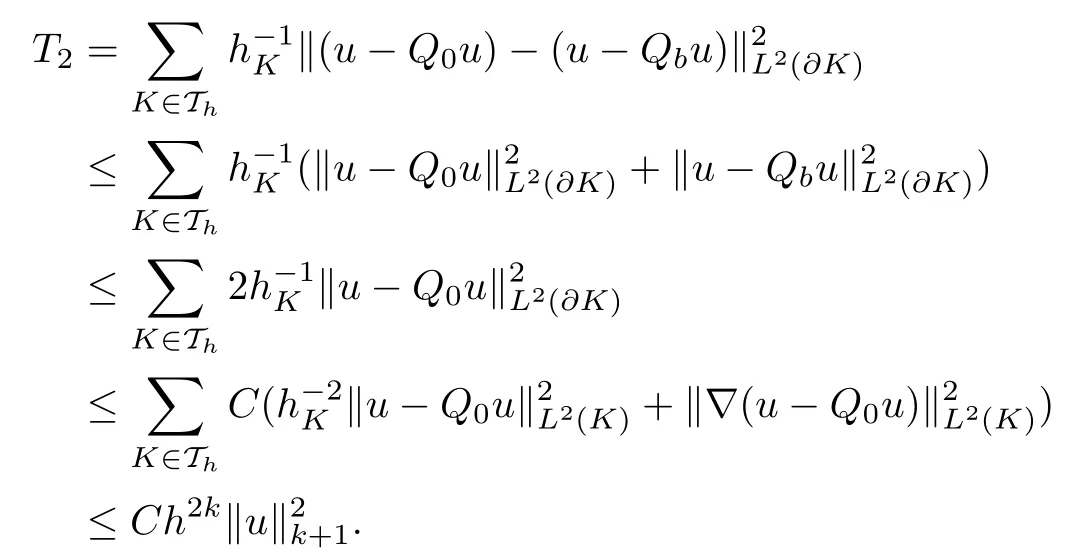
As for T3, it follows from the triangle inequality, (3.3) and Lemma 3.2 that

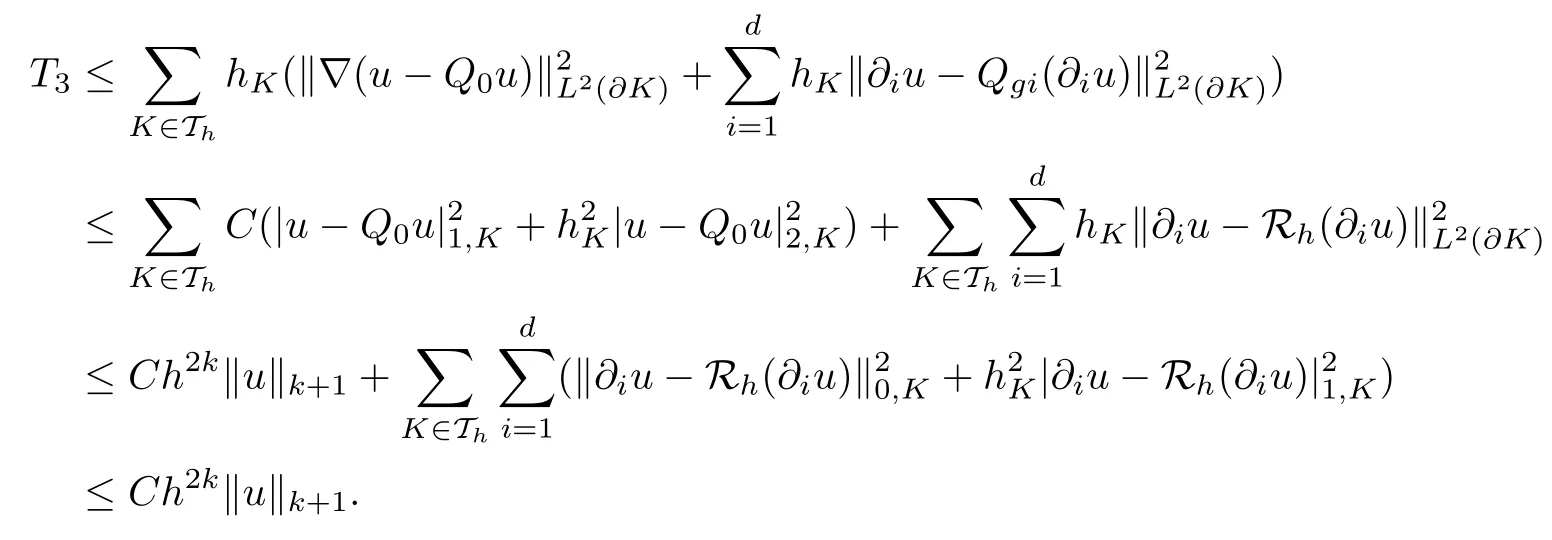
Combining the estimates of T1, T2and T3completes the proof.

Theorem 3.6Assume that the coefficient tensor A(x) is uniformly bounded on ?. Let u ∈ Hk+1(?) and uhbe the solutions of problems (1.1) and (2.5), respectively. Qhu is the L2projection of u onto the finite element spaceThen there exists a positive constant C such that

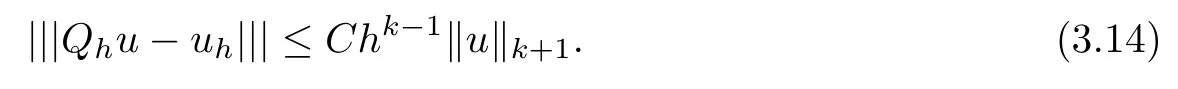
Furthermore, if A(x) is constant or piecewise constant on ?, we have

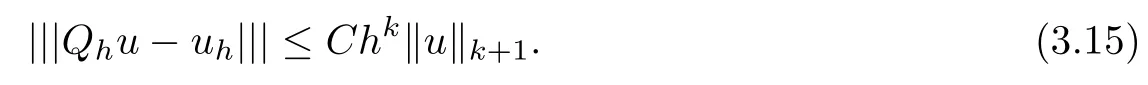
ProofLetting v =ehin (3.7), we have

It then follows from (3.9) and (3.10) that

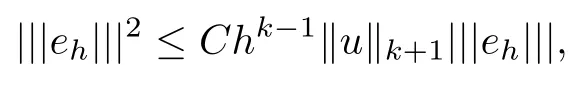
which implies (3.14).

If A(x) is constant or piecewise constant, it follows from the property of L2projection operator Rhthat ?u(eh)=0. Then (3.9) yields (3.15). This completes the proof.

Theorem 3.7Assume that the coefficient tensor A(x) is uniformly bounded on ?. Let u ∈ Hk+1(?) and uhbe the solutions of problems (1.1) and (2.5), respectively. Then there exists a positive constant C such that

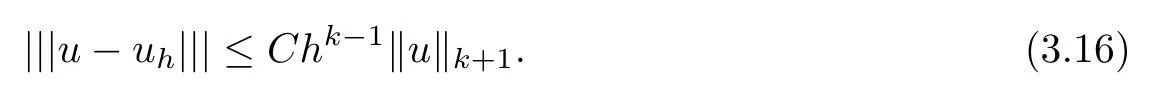
Furthermore, if A(x) is constant or piecewise constant on ?, we have

ProofBy the triangle inequality, we have

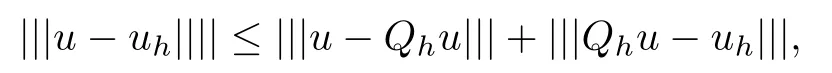
which, together with Theorem 3.5 and Theorem 3.6, completes the proof.

4 Numerical Experiments

In this section, we present some numerical examples for the LS-WGM presented in Section 2. In the experiments that follows, we employ a rectangular mesh and the WG element with k = 2 in (2.1). We will find an approximate solution uh= {uh,0,uh,b,uh,g} in finite element spacefor problem (1.1) using LS-WGM.

Example 1A(x) is a constant matrix Taking ? = (0,1)2, a non-divergence form elliptic problem(1.1)is considered with the following two coefficient tensors A(x)=Ai,i=1,2:

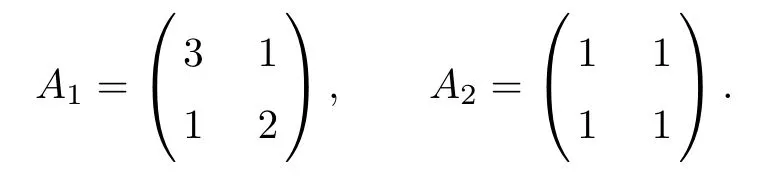
Here we have chosen f such that the exact solution is u(x1,x2)=sin(πx1)sin(πx2).

Table 1 presents the errors and convergence rates in the L2-norm, H1-norm, and H2-equivalent norm |||·||| for the two different coefficient matrices, A1and A2, respectively. It shows that the errors in the |||·||| norm are superconvergent of order O(h2), even if coefficient matrix A is singular. Moreover, the errors in the H1-norm and L2-norm are convergent with an optimal rate of O(h2) and O(h3), respectively.

Table 1 Convergence test of the LS-WGM scheme with k =2 on a rectangular mesh

Example 2A(x) is a continuous matrix-valued function In this example,we take A(x) as the following continuous matrix-valued function:

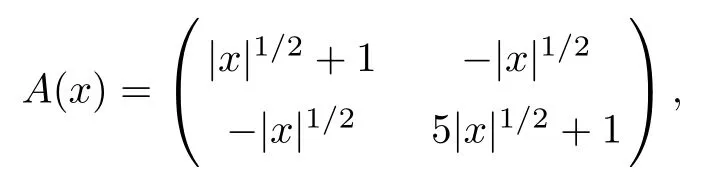
Table 2 gives the computed results for the case in which the coefficient matrix A(x) is a continuous matrix-valued function. Exceeding our expectations, the convergence rate in the|||·||| norm is also superconvergent of order O(h2) for this example. The numerical results suggest that the convergence rates in the L2-norm and H1-norm are optimal for O(h3) and O(h2), respectively.

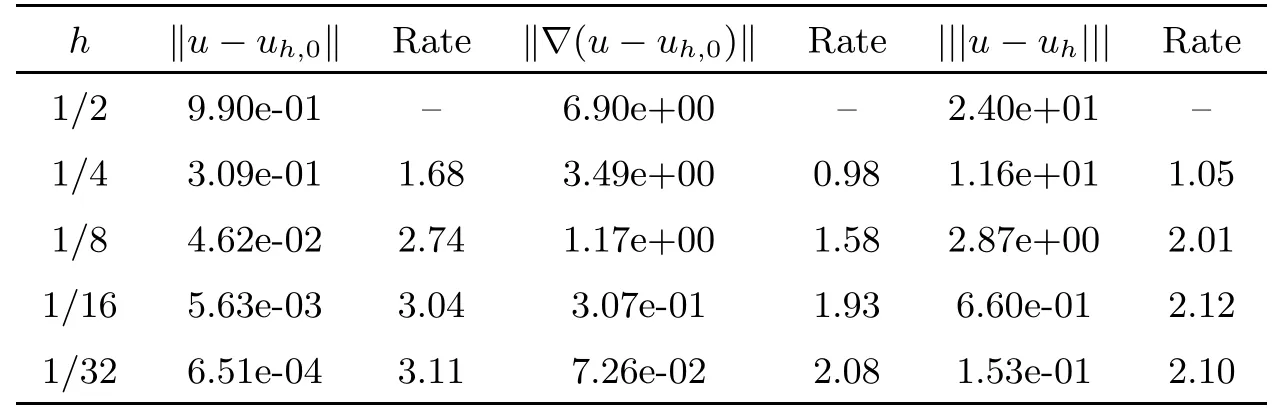
Table 2 Convergence test of the LS-WGM scheme with k =2 on a rectangular mesh

Example 3A(x) is a piecewise constant matrix Let ? = (?1,1)2and take A(x)as follows:

where f is chosen so that the exact solution is

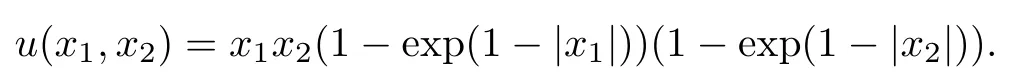
The coefficient matrix A(x) is discontinuous across the set D ={x ∈?:x1=0 or x2=0}.

Table 3 gives the L2,H1,and|||·|||errors and the convergence rate for the case in which the coefficient matrix A(x)is a discontinuous matrix-valued function. The numerical results suggest the convergence rate in L2, H1, and |||·||| norm are O(h3),O(h2), and O(h2), respectively.

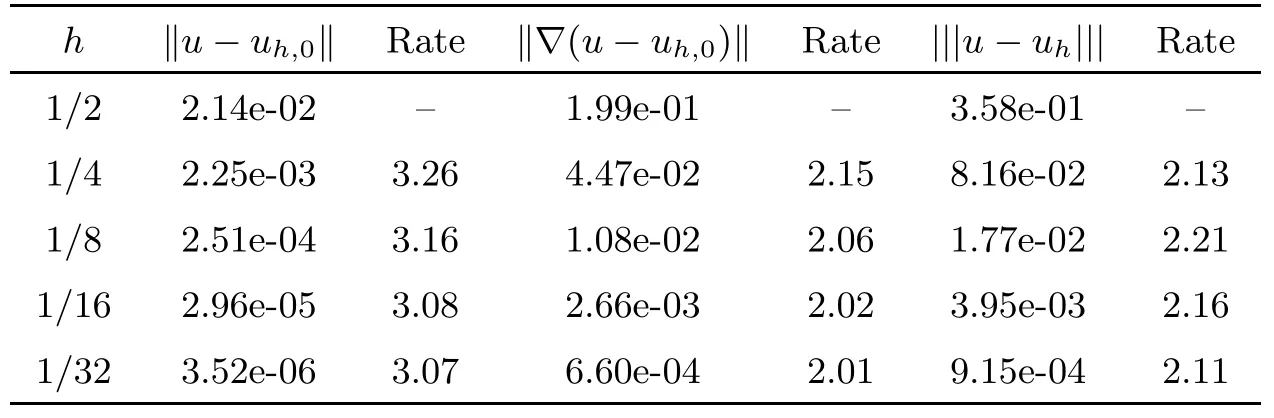
Table 3 Convergence test of the LS-WGM scheme with k =2 on a rectangular mesh

5 Conclusion

We have presented a simple and robust numerical method for the second order elliptic equation in non-divergence form, which is designed within the least square framework and uses the weak Hessian concept from the weak Galerkin finite element method. Convergence analysis of our numerical scheme is established on an arbitrary shape regular polygonal mesh. Numerical results indicate that our numerical scheme is optimally convergent in the L2norm and the H1norm, and that it is superconvergent in the H2equivalent norm |||·|||.