Constitutive modeling of the magnetic-dependent nonlinear dynamic behavior of isotropic magnetorheological elastomers

Bochao Wang,Yan Li,Haoming Pang,Zhenbang Xu,and Xinglong Gong ?

1CAS Key Laboratory of Mechanical Behavior and Design of Materials, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China;

2CAS Key Laboratory of On-orbit Manufacturing and Integration for Space, Optics System, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

Abstract: Isotropic magnetorheological elastomers (MREs) are smart materials fabricated by embedding magnetizable particles randomly into a polymer matrix.Under a magnetic field,its modulus changes rapidly,reversibly,and continuously,offering wide application potential in the vibration control area.Experimental observations show that there is a strong frequency,strain amplitude,and magnetic dependence of the dynamic behavior of isotropic MRE.Although important for potential applications,the magnetic-dependent nonlinear dynamic behavior of isotropic MRE has received little theoretical attention.To accurately evaluate the dynamic performance of isotropic MRE and to guide the design of isotropic MRE-based products,a new constitutive model based on continuum mechanics theory is developed to depict the magneticdependent nonlinear dynamic behavior of isotropic MRE.Subsequently,the numerical implementation algorithm is developed,and the prediction ability of the model is examined.The model provides a deeper understanding of the underlying mechanics of the magnetic-dependent nonlinear viscoelastic behavior of isotropic MRE.Furthermore,the model can be utilized to predict the magnetomechanical coupling behavior of isotropic MRE and therefore serves as a useful platform to promote the design and application of isotropic MRE-based devices.

Keywords: isotropic magnetorheological elastomer;frequency dependence;strain amplitude dependence;magnetic dependence;nonlinear viscoelasticity;constitutive modeling

1 Introduction

Magnerheological elastomers (MREs) are smart materials that are often fabricated by embedding magnetizable particles into a polymer matrix.Under a magnetic field,due to the interaction between particles and the matrix,magnetic tunability of the modulus can be achieved for MRE.By utilizing the magnetic tunability of the modulus,applications of MRE in semiactive vibration isolators[1-3],smart tuned mass dampers[4,5]and vibration absorbers[6]have been explored.Meanwhile,since the magnetic permeability of MRE is larger than that of rubber and air,a stress mismatch occurs and results in magnetostriction of MRE if a magnetic field is applied.Due to magneto-induced deformation,a magnetically controlled surface pattern[7,8]using MRE is exploited.

To guide the design of MRE-based products,accurate characterization and modeling of their dynamic behavior is needed.Experimentally,a dynamic test of isotropic MRE under harmonic cyclic loading shows that the modulus of MRE increases with magnetic field and frequency but decreases with strain amplitude[9,10].On the other hand,the stress relaxation test of isotropic MRE shows that a longer time is needed for it to reach the equilibrium state when a magnetic field is applied[11,12].Therefore,due to the coupling between particles and the matrix within the isotropic MRE under magnetic and mechanical loadings,a complex,magneticdependent nonlinear dynamic behavior is exhibited.

Theoretically,magnetic dipole theory[13]was initially utilized to depict the modulus magnetic stiffening effect of MRE under the quasistatic case.Next,the distribution of the particle chain[14]and inelastic behavior of isotropic MRE were taken into account through the Zener viscoelastic element[15,16],friction element[17],and fractional dashpot element[18,19]based on the infinitesimal strain assumption.Afterwards,based on the phenomenological model of MRE,the dynamic performance of MRE-based devices was modeled,e.g.,Refs.[20,21].However,due to the soft nature of the matrix,magnetic dipolebased theory cannot predict the dynamic behavior of MRE under large deformation.A finite strain magnetoelastic interaction theory was developed by Dorfmann and Ogden[22].It is postulated that Helmholtz free energy exists for isotropic MRE and that the derivative of the free energy with respect to the deformation gradient and the magnetic field strength results in the corresponding stress and magnetic flux density,respectively.Following the theoretical path of Dorfmann and Ogden[22],constitutive models that incorporate the magnetization behavior and the contribution of Maxwell stress to the total stress within isotropic MRE were developed[23,24].Subsequently,the corresponding finite element implementation platform was developed and used to predict the magnetostriction-induced deformation of an isotropic MRE film bonded to a nonmagnetic substrate[25-27].However,for the model developed[21,22],the effect of the magnetic field is coupled to the classical hyperelastic model in an additive form,and the modulus magnetic stiffening effect is only exhibited in directions where the Maxwell stress is not zero.However,experimental testing results showed that a modulus magnetic stiffening effect also existed in other directions.Therefore,the modulus magnetic stiffening effect cannot be represented fully by the model developed.

Currently,theoretical works have mainly focused on predicting the rate-independent behavior of isotropic MRE.As an essential component of the mechanical behavior of MRE and which is of great importance to the application of isotropic MRE in the vibration control area,the dynamic behavior of MRE has received little attention.Constitutive models to depict the hysteresis behavior of isotropic MRE mainly focus on the magnetic-dependent viscoelastic behavior based on an infinitesimal strain assumption by adding a dashpot or viscoelastic Zener model[15-19].Although a finite strain-based Zener viscoelastic element[28-30]was introduced to account for the viscoelastic behavior of the polymer matrix,the viscosity of the Zener viscoelastic element was assumed to be a constant value,irrespective of the magnetic field and strain amplitude.However,as observed experimentally[9-12],the viscoelastic behavior of isotropic MRE is highly magnetic and strain amplitude dependent.Therefore,there is a certain gap between the experimental testing and constitutive modeling of isotropic MRE.

To evaluate the dynamic performance of isotropic MRE under different frequencies,strain amplitudes,and magnetic fields and to guide the design of MRE-based devices,a new constitutive model of MRE that incorporates magnetic,frequency,and amplitude dependency is developed based on experimental testing and theoretical analysis.The major novelty of this study is to develop a new constitutive model based on finite strain theory that thoroughly incorporates the modulus magnetic stiffening effect and the nonlinear viscoelasticity of isotropic MRE.This work can provide guidance for the accurate prediction of the magnetomechanical coupling behavior of isotropic MRE and promote the design and possible applications of isotropic MRE-based devices.

The remainder of this paper is organized as follows.In Section 2,quasistatic,magnetization,and harmonic cyclic dynamic tests of MRE are conducted.In Section 3,the continuum mechanics framework is introduced.Afterwards,the specific constitutive equations are proposed in Section 4.In Section 5,the experimental and simulation results are compared;furthermore,the model prediction results are presented.Finally,the conclusion is presented in Section 6.

2 Experimental results

Carbonyl iron particles (CIPs,type CN,BASF,Germany diameter 7 μm on average),polydimethylsiloxane (PDMS),and curing agent are used.The mass ratio for carbonyl iron particles,PDMS,and curing agent is 75∶25∶1.The specific fabrication process is as follows.First,PDMS,curing agent,and carbonyl iron particles are mixed for 5 min.Afterwards,the air bubbles within the mixture were extracted using a vacuum chamber for half an hour.Subsequently,the mixture was poured into a rectangular mold and vulcanized at 100 °C for half an hour.During curing,no magnetic field is applied.Therefore,the carbonyl particles are assumed to be homogenized and distributed within the matrix,and the fabricated MRE is isotropic.The schematic configuration corresponding to the fabrication process of isotropic MRE is shown in Fig.1.For more details regarding the fabrication of isotropic MRE,the readers are referred to Ref.[31].

Fig.1. Schematic configuration for the fabrication of isotropic MRE.

After fabrication,a quasistatic test of the isotropic MRE with a strain rate of 3×10-5s-1and strain amplitude of15%under magnetic fields with magnitudes of 0,0.2 T,and 0.4 T are conducted on a dynamic mechanical analyzer.For the dynamic test,0.1 Hz,1 Hz,and 10 Hz are considered,three sets of strain amplitudes of 5%,10%,and 15% and two sets of magnetic fields of 0 and 0.4 T are applied.An Electroforce 3200-type dynamic mechanical analyzer (DMA) from TA instruments with the function of applying a magnetic field,as shown in Fig.2,is used to test the magnetic-dependent mechanical behavior of isotropic MRE.Before testing,the relation between the magnetic flux density and applied current was calibrated through a Tesla meter.Each combination of frequency,strain amplitude,and magnetic field is tested three times,and the mean value is taken as the final test data.

Fig.2. Dynamic mechanical analyzer with function of applying magnetic field.(a) Photograph of the dynamic mechanical analyzer.(b) Schematic configuration of the dynamic mechanical analyzer.

To characterize the magnetization performance of MRE,a hysteresis measurement of soft and hard magnetic materials(HyMDC Metis,Leuven,Belgium) was utilized.After testing,the measurement results are shown in Figs.3-5.

The results in Fig.3 show that a pronounced modulus magnetic stiffening effect is exhibited for isotropic MRE.Furthermore,the quasistatic behavior of isotropic MRE is nonlinear.Specifically,the slope of the stress-strain curve decreases first,then reaches a linear region,and afterwards,there is another increase in the slope.From the perspective of modeling,a hyperelastic model that is able to depict the nonlinear stress -strain curve is needed.Regarding the magnetization curve,it is found that the magnetization strength increases with increasing magnetic field intensity until magnetic saturation is reached for isotropic MRE.

Fig.3. Quasistatic stress-strain test results of isotropic MRE under different magnetic fields and the magnetization strength-magnetic field intensity curve of isotropic MRE.The lines and dots are experimental and simulation results,respectively.

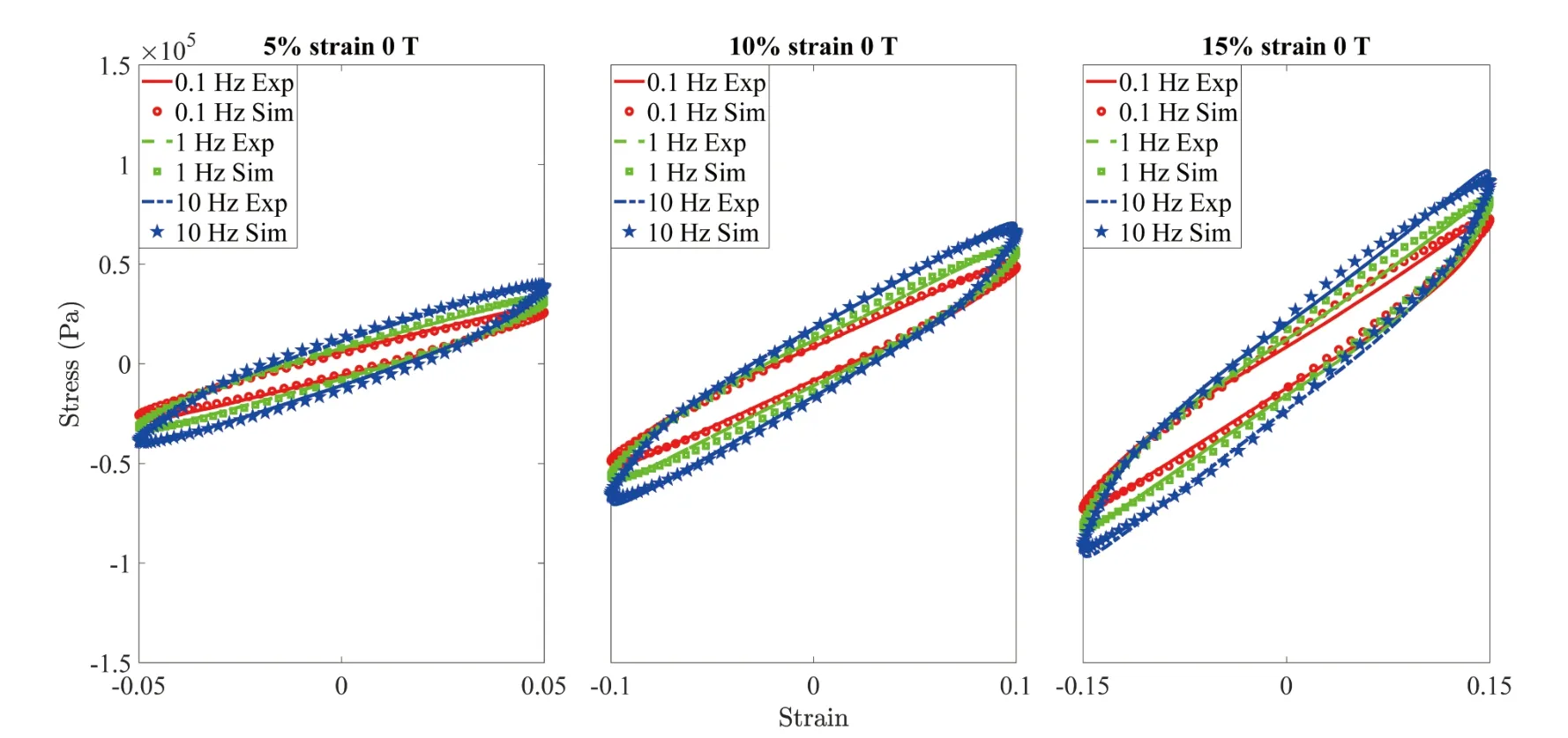
Fig.4. Dynamic hysteresis stress-strain of isotropic MRE under different frequencies and strain amplitudes.The magnetic field is 0 T.The lines and dots are the experimental and simulation results using the modified Eyring viscoelastic model,respectively.

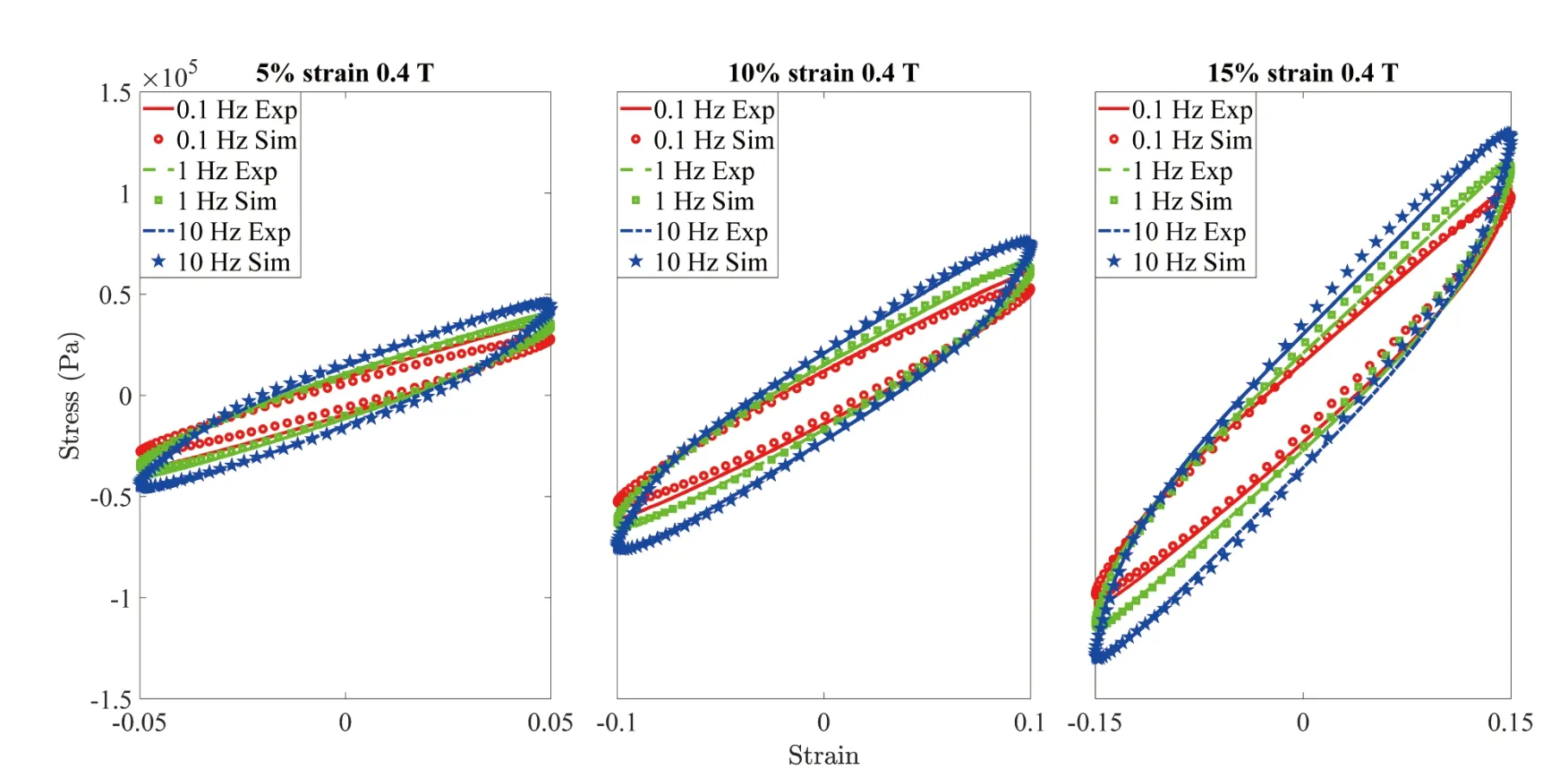
Fig.5. Dynamic hysteresis stress-strain of isotropic MRE under different frequencies and strain amplitudes.The magnetic field is 0.4 T.The lines and dots are the experimental and simulation results using the modified Eyring viscoelastic model,respectively.

Regarding the dynamic hysteresis stress-strain curve,as shown in Figs.4 and 5,the peak stress increases with increasing magnetic field,frequency,and strain amplitudes.To quantitatively evaluate the influence of the strain amplitude on the dynamic behavior of isotropic MRE,the Fourier transform-based method is applied to extract the equivalent shear modulus and loss factor of isotropic MRE in the frequency domain.Mathematically,the equivalent shear modulus and loss factor of the MRE are reached through

whereG?,G′,andG′′denote the complex,storage,and loss moduli,respectively.τ and γ are the Fourier transforms of the shear stress and shear strain in the frequency domain.|G?|is the equivalent shear modulus,and η is the equivalent loss factor.After applying Eqs.(1)-(3),the equivalent storage and loss modulus of the isotropic MRE is shown in Fig.6.Clearly,the equivalent modulus and the loss factor of the isotropic MRE decrease with increasing strain amplitude.Microscopically,this phenomenon is closely related to the deformation-enhanced shear thinning of the polymer.From a constitutive modeling perspective,a strain amplitude and magnetic field process-dependent nonlinear viscoelastic model is needed to depict the nonlinear and magneticdependent dynamic behavior of isotropic MRE.

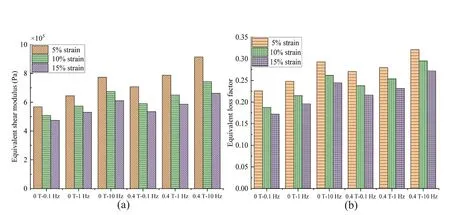
Fig.6. Equivalent shear modulus (a) and loss factor (b) of isotropic MRE in the frequency domain under different strain amplitudes and magnetic fields.

3 Continuum mechanics basis

3.1 Kinematics and magnetic equations

Due to the soft nature and large deformation that isotropic MRE may encounter during application,continuum mechanics theory should be applied to depict the magnetomechanical coupling behavior of isotropic MRE.As shown in Fig.7,the initial configuration of the isotropic MRE where no loading is applied is denoted as ?reference.After loading,the isotropic MRE moves from ?referenceto ?current.The deformation gradient that connects ?referenceand ?currentis

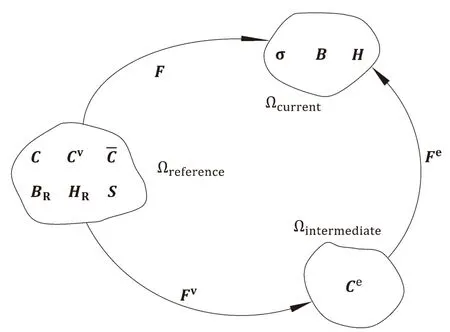
Fig.7. Illustration of the kinematic frame of isotropic MRE.

where χ is the motion of a specific material point with coordinatesXandxin the reference and current configuration,respectively.The corresponding right Cauchy-Green tensor isC=FTF,where superscript T denotes the transpose of the matrix.To depict the viscoelastic behavior of isotropic MRE,following the theoretical path of finite strain viscoelasticity[32-34],the deformation gradient is further multiplicatively decomposed into a viscous (Fv) and an elastic part (Fe)asF=FeFv.The corresponding right Cauchy-Green tensors areCe=(Fe)TFeandCv=(Fv)TFv.

Furthermore,as shown in Fig.7,the magnetic flux density and magnetic field intensity in ?referenceareBRandHR.According to the magnetoelastic interaction theory by Dorfmann and Ogden[22],the equivalent interactions in ?currentareBandHwith

According to Ref.[22],the boundary conditions satisfied forBandHare

where [[(·)]]=(·)outside-(·)MREdenotes the difference between the outside surroundings and MRE.nis the normal direction at the MRE and surrounding air interface along the applied magnetic flux density direction.In vacuum,BandHare connected byB=μ0H,where μ0=1.256×10-6T·m·A-1is the magnetic permeability in vacuum.Furthermore,Sin Fig.6 denotes the second Piola-Kirchhoff stress in the reference configuration,and it is connected to the Cauchy stress by

withJ=det(F).

3.2 Thermodynamic framework

In this work,no temperature change is considered.Therefore,an isotropic MRE is assumed under isothermal conditions.Temperature has a significant effect on the mechanical dynamic behavior of polymer-based materials.The coupling of the temperature-dependent magnetomechanical behavior of isotropic MRE may be taken into account in the current model through the time-temperature equivalence principle[35]or the Williams-Landau-Ferry function[36],which will be one of the future research directions following this work.Under isothermal conditions,it is postulated that a Helmholtz free energy Φ exists within the MRE and is a function ofCandHR.To depict the magnetization behavior,the modulus magnetic stiffening effect,the viscoelastic behavior along with the contribution of the Maxwell stress on the total stress,Φ is decoupled into three parts as:

where Φme,Φmve,and Φmare the magnetohyperelastic,magnetoviscoelastic,and pure magnetic free energy parts,respectively.According to Ref.[30],the Clausius-Planck inequality of thermodynamics that must be satisfied is

where the dot between two vectors represents the scalar product operator,two dots are the second-order tensor contraction operator and the superscript dot represents the material time derivative.Inserting Eq.(11) into Eq.(10) and keeping in mind that (Ce,HR) instead of (C,HR) determines Φmve,the following can be obtained:

and a dissipation equation

wherebv=FvFvTis the left viscous Cauchy-Green strain tensor.By defining ￡vbe=the well-known Clausius-Planck thermodynamic inequality for the finite strain viscoelasticity is obtained

To fulfil the condition in Eq.(17),the evolution law for￡vbe·(be)-1is set to be

where dev denotes the deviatoric operator with dev(·)=(·)-1/3×tr(·),with tr being the trace operator of second-order tensors.

4 Constitutive equations and numerical implementation method

After introducing the continuum mechanics frame and magnetic equations,the specific constitutive equations to depict the modulus magnetic stiffening effect,the magnetization behavior,and the magnetic-dependent viscoelastic behavior of isotropic MRE will be represented in this section.First,a new type of multiplicatively coupled magneto-hyperelastic free energy function is proposed.Afterwards,a nonlinear viscoelastic constitutive model to depict the rate,magnetic,and strain amplitude dependence of isotropic MRE is developed.Finally,the numerical implementation algorithm corresponding to the nonlinear viscoelastic constitutive equations will be introduced.

4.1 Magnetization and magneto-hyperelastic constitutive model

To depict the magnetization behavior,as shown in Fig.3,the representation theory of tensors is utilized.According to Refs.[29,30],the tensor invariant

is used to depict the magnetization behavior of isotropic MRE.Physically,it is the square of the norm of the magnetic field intensity in the current configuration.To depict the magnetic saturation behavior of the magnetic hysteresis curve,as shown in Fig.3,the pure magnetic free energy Φmis set to be

where the first term in Φmis used to depict the magnetization behavior of isotropic MRE and the second term is used to depict the contribution of Maxwell stress on the total stress.The constantsm0andm1are material parameters that need to be determined through experimental testing.Specifically,by the results in Eqs.(12) and (13),

By pushing forward the result in Eqs.(21) and (22) into the current configuration,it is obtained that

whereIis the second-order unit tensor.By observing the result in Eq.(23),an additional term along the direction ofH?Hcontributes to the total stress in addition to the classical Maxwell stress tensorHowever,it should be noted that the modulus magnetic stiffening effect of isotropic MRE cannot be represented thoroughly merely through Eq.(20).The underlying reason is that the modulus magnetic stiffening effect only works in directions alongH?H.However,as shown in Fig.3,a pronounced modulus magnetic stiffening effect was also exhibited in other directions.Therefore,an additional magnetomechanical coupled free energy term is needed to depict the modulus magnetic stiffening effect of isotropic MRE thoroughly.According to Refs.[22,23],an additional tensor invariant

is used.It allows the magnetic field coupling to the original hyperelastic free energy in a multiplicative way by

where Φeis the classical hyperelastic free energy for the rubber matrial.gmeandMs_eare material parameters that reflect the enhancement effect of the applied magnetic field on Φe.The experimental results show that the stress increases with increasing magnetic field until magnetic saturation is reached.Therefore,the hyperbolic tangent function is used in Eq.(26)to depict this trend.As shown in Fig.3,there is a stress stiffening effect at a large strain amplitude (10%-15%).Therefore,the Yeoh hyperelastic model[37]uses this effect.Subsequently,Eq.(26) is shown in an explicit way as

whereI1=I:Cis the first principal scalar tensor invariant forCand μeis the classical shear modulus.Next,the corresponding Cauchy stress and the magnetic flux density are

whereb=FFTis the left Cauchy-Green strain tensor.

4.2 Magneto-viscoelastic constitutive model

Following the same path for the magneto-hyperelastic free energy term,the free energy for the magneto-viscoelastic part is expressed as

Inserting Eq.(31) into Eq.(18),an alternative form for￡vbe·(be)-1to satisfy the thermodynamic inequality is obtained

4.3 Numerical implementation algorithm for the magneto-viscoelastic constitutive model

To ease the reader’s understanding,the constitutive equations for the magneto-viscoelastic model are listed below:

The constitutive equations listed in Eq.(34) are highly nonlinear.To solve Eq.(34),the operator split methodology,which is widely utilized in finite strain inelasticity,is applied.From the perspective of numerical implementation,there are three main steps.Taking the time interval (tn，tn+1) as an example.First,for the elastic trail step,it is assumed that there is no updating ofCvfromtntotn+1.Therefore,trialbeand the correspondingand ￡be·(be)-1can be determined.vSecond,for the residual check step,the residual corresponding to ￡vbe·(be)-1is checked.Finally,for the inelastic corrector step,if the residual does not meet the threshold requirement,Cvwill be updated by using the Newton-Rapson method.Since the whole process is highly mathematically involved,the detailed derivation is not shown.To keep the manuscript compact,only the numerical implementation flowchart is shown.For more details regarding the operator split method,the readers are referred to Ref.[34].

(Ⅰ) Elastic trial:

where eig denotes the matrix eigen decomposition,andnaare the eigenvalue and eigenvectors,respectively.

(Ⅱ) Residual check: ifr≤tol,where tol is the threshold,then (Cv)n+1=(Cv)n.Else go to step Ⅲ.

(Ⅲ) Inelastic correction:

whereKmve=?r/??e. Updating ?e,until the requirementr≤tol is met.

(Ⅳ) Export output:

For readers to understand the numerical implementation method,a flow chart corresponding to Eq.(34) to Eq.(38) is shown in Fig.8.

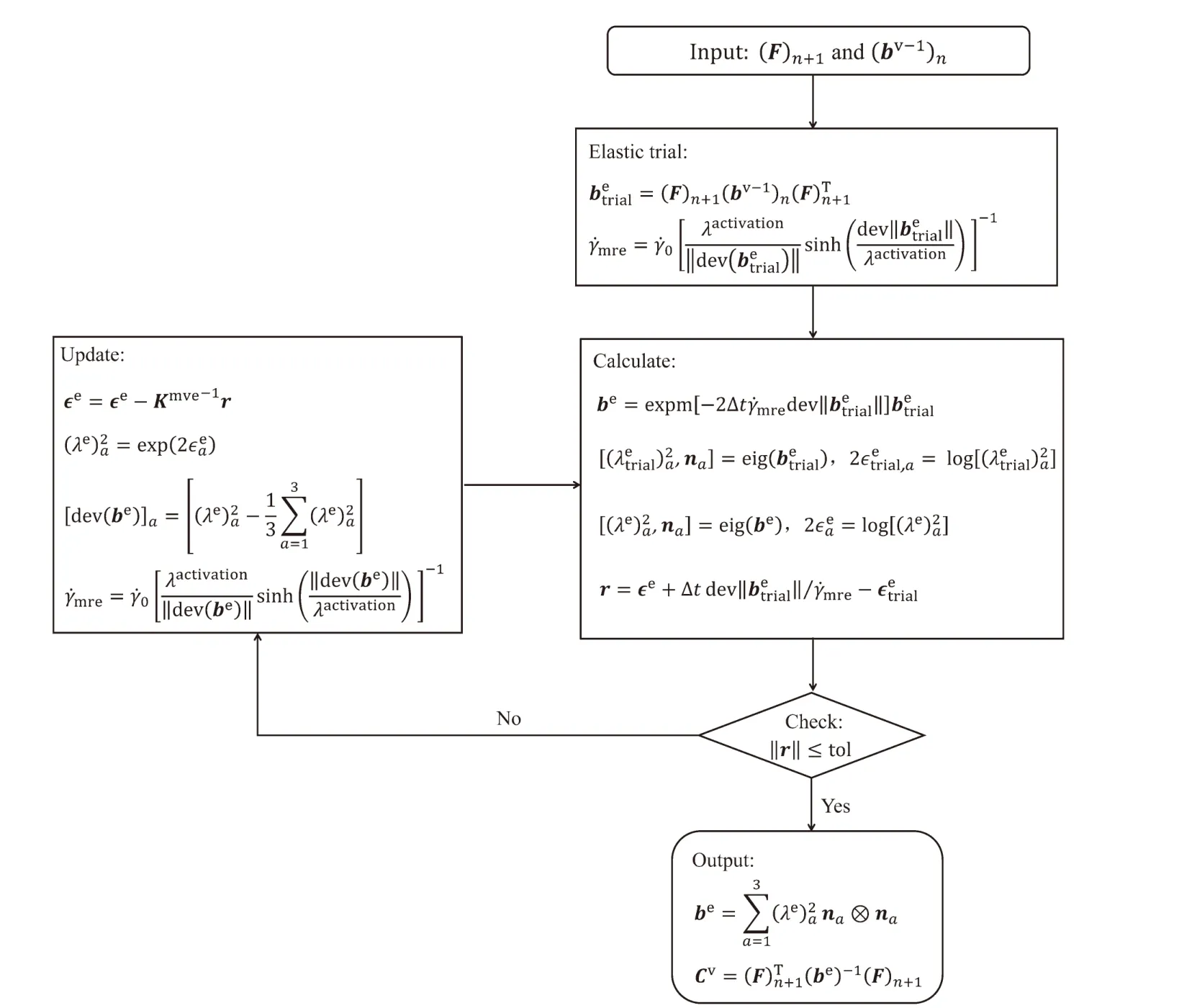
Fig.8. Flow chart corresponding to the numerical algorithm from Eqs.(34) to (38).

5 Parameter identification and model prediction results

In this section,the boundary problem solution corresponding to the simple shear quasistatic and dynamic tests of isotropic MRE,as shown in Figs.3 and 5,will be derived.Afterwards,the material parameters corresponding to the constitutive equations in Eqs.(20),(27),and (34) will be identified.Subsequently,simulation results and experimental test results will be compared.Finally,two model prediction results are shown.

5.1 Boundary value problem solution and parameter identification

An illustration of the simple shear test setting with an applied magnetic field is shown in Fig.9.Since carbonyl iron particles are assumed to be randomly distributed within the polymer matrix,isotropic MRE is viewed as a homogenized material.The deformation gradient corresponding to the simple shear test is

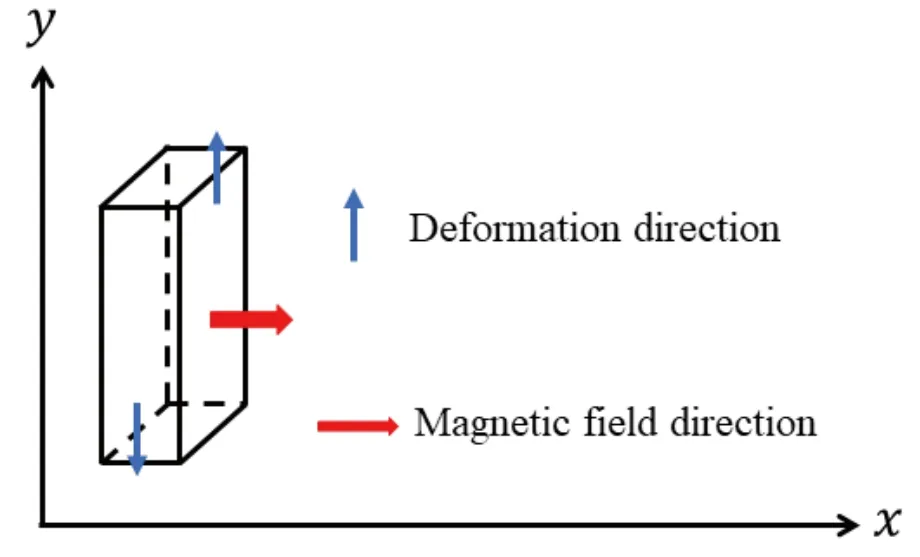
Fig.9. Illustration of the simple shear testing setting with an applied magnetic field for isotropic MRE.

Fig.10. Comparison between experimental (Exp) and simulation (Sim) stress-strain hysteresis results by the classical Maxwell viscoelastic model for isotropic MRE at zero magnetic field with different frequencies and strain amplitude.The lines and dots are experimental and simulation results,respectively.

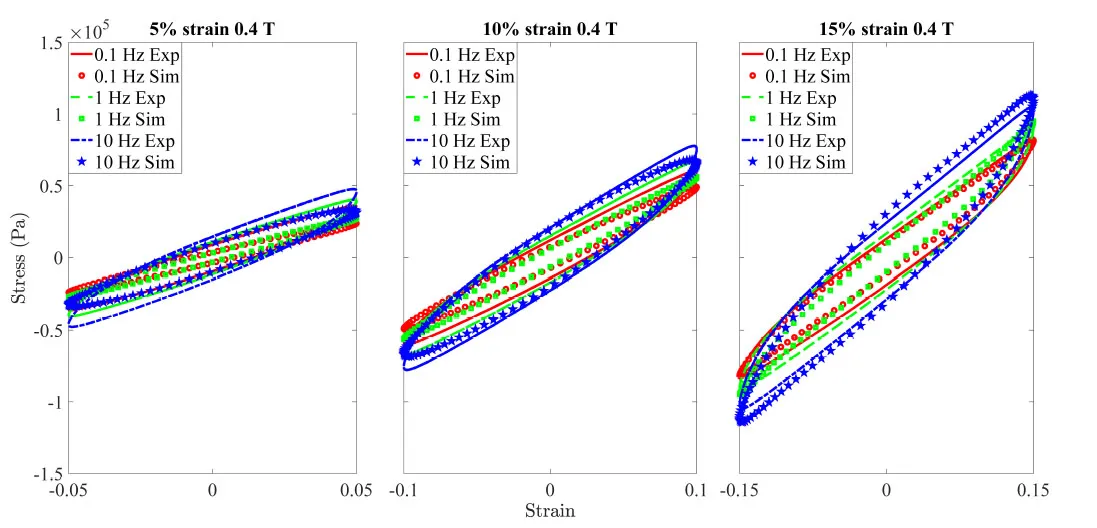
Fig.11. Comparison between experimental (Exp) and simulation (Sim) stress-strain hysteresis results by the classical Maxwell viscoelastic model for isotropic MRE at 0.4 T magnetic field with different frequencies and strain amplitude.The lines and dots are experimental and simulation results,respectively.

where γ is the shear strain amplitude.The magnetic field applied is

where variables with a superscript+represent the value within surrounding air.The normal direction along the magnetic field at the MRE-air interface is

The results in Eqs.(6) to (8) result in

where variables with subscripts denote values within the MRE.Inserting Eqs.(39) and (42) into Eqs.(23),(24),(28),and (29) result in

H+is a prior known value.Numerically,the solution ofH1is solved using the fsolve function in MATLAB?(MATLAB Release 2015b,The MathWorks,Inc.,Natick,Massachusetts,United States).

Identifying the material parameters to depict the magnetomechanical performance of isotropic MRE.The nonlinear least square method with function lsqnonlin in MATLAB?(MATLAB Release 2015b,The MathWorks,Inc.,Natick,Massachusetts,United States) is utilized to minimize the objective function (obj):

whereyrealandyestimateare the tested and predicted results,respectively,and conj represents the conjugate operator.

First,the magnetization curve shown in Fig.3 and Eq.(24)is utilized to obtain parametersm0andm1.After obtainingm0andm1,the magnetic independent material parameters μe,d2,andd3are obtained through the quasistatic stress-strain result at 0 T and Eq.(44) withgme=0.Next,magneticdependent material parametersgmeandMs_meare identified through the quasistatic stress-strain results at 0.2 T and 0.4 T and Eq.(44).The identified material parameters are listed in Table 1.The comparison between the measurement and simulation results is shown in Fig.3.Clearly,the proposed multiplicatively formed magneto-hyperelealstic free energy in Eq.(27) along with the pure magnetization free energy as shown in Eq.(20) can depict the magnetization and modulus magnetic stiffening effect of isotropic MRE accurately.

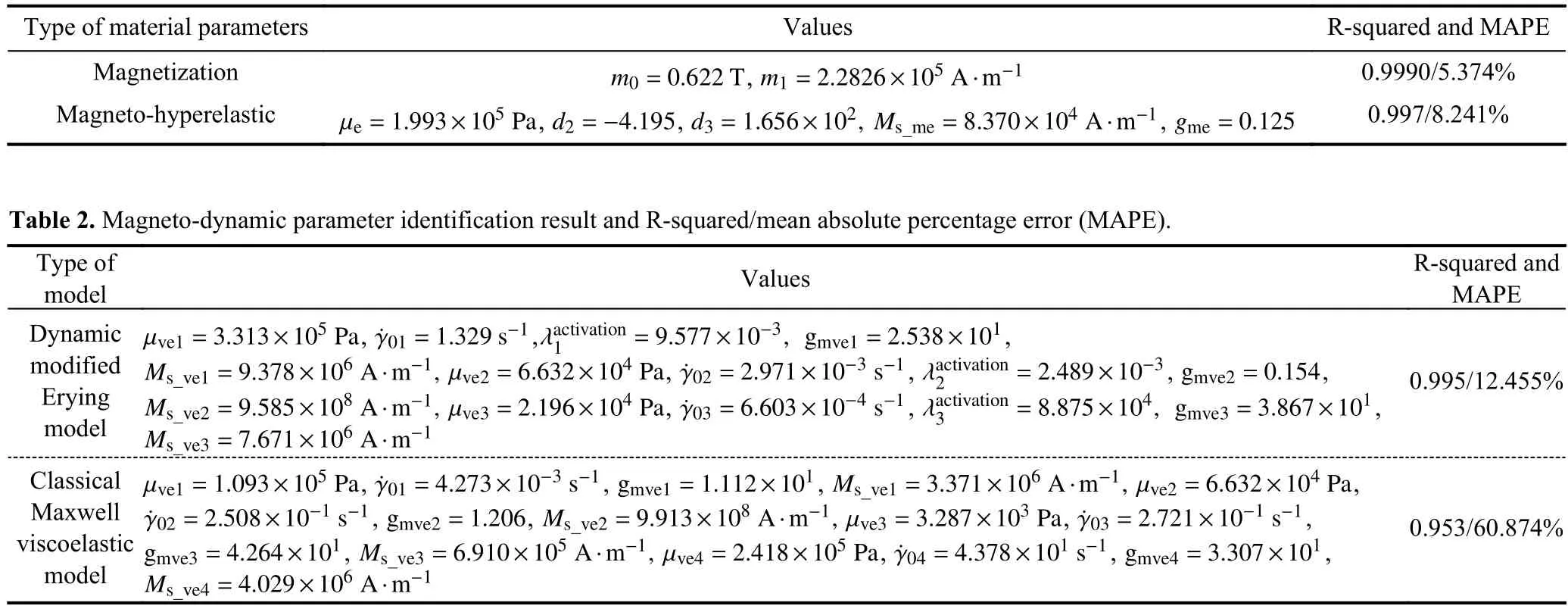
Table 1. Magneto-hyperelastic parameter identification result and R-squared/mean absolute percentage error (MAPE).

After obtaining the magnetization and quasistatic related material parameters,three sets of modified Eyring viscoelastic elements,as shown in Eq.(34),are utilized to simulate the dynamic behavior of isotropic MRE. First,magnetic independent material parameters μve,and λactivationare identified using the dynamic hysteresis stress-strain data at 0 T under 0.1 Hz,1 Hz,and 10 Hz.Afterwards,magneticdependent material parameters gmveandMs_mveare identified using the dynamic hysteresis stress-strain data at 0.2 T and 0.4 T under 0.1 Hz,1 Hz,and 10 Hz and the nonlinear viscoelastic model in Eq.(34).The specific values of the identified material parameters are shown in Table 2.The comparison between the experimental and simulation results is shown in Figs.4 to 5.Clearly,the proposed magnetic field-,strain amplitude-,and frequency-dependent finite strain viscoelastic model can depict the dynamic behavior of isotropic MRE with accuracy.To demonstrate the advantage of the model developed in this paper,four sets of classical Maxwell viscoelastic elements with magnetic dependence,which are commonly used for the current constitutive modeling study of isotropic MRE[25,27,29,30],were utilized to depict the hysteresis stress-strain results.Mathematically,the modified Eyring viscoelastic model degraded into the classical Maxwell viscoelastic model without strain dependence when λactivationin Eq.(34) approaches infinity.The comparison result is shown in Figs.10 and 11 with the identified material parameters,Rsquared and mean absolute percentage error shown in Table 2.Obviously,the fitting effect of the classical Maxwell viscoelastic element to depict the magnetic nonlinear viscoelastic behavior of isotropic MRE is not good even when one more material parameter is used.Specifically,the details of the stress-strain variation cannot be well described by the classical Maxwell viscoelastic element,although the maximum magnitude in the stress strain curve can be depicted.The underlying reason is that the classical viscoelastic model can only depict the rate dependency and is unable to replicate the strain amplitude-dependent dynamic behavior of isotropic MRE.

5.2 Model prediction

To further illustrate the effect of the strain rate,strain amplitude and magnetic field on the dynamic performance of the material.Two sets of model predictions are conducted.For the first set,isotropic MRE are loaded with different strainrates (0.0004,0.02,0.1,0.4,2,and 10 s-1).The strain amplitude is fixed to 0.1,and two kinds of magnetic fields,0 and 0.4 T,are considered.The time versus stress results are shown in Fig.12.Obviously,a larger peak stress is exhibited if a faster strain loading rate is applied.Furthermore,it can be found that the peak stress increases with increasing magnetic field,which again verifies the validity of the model to replicate the modulus magnetic stiffening effect.

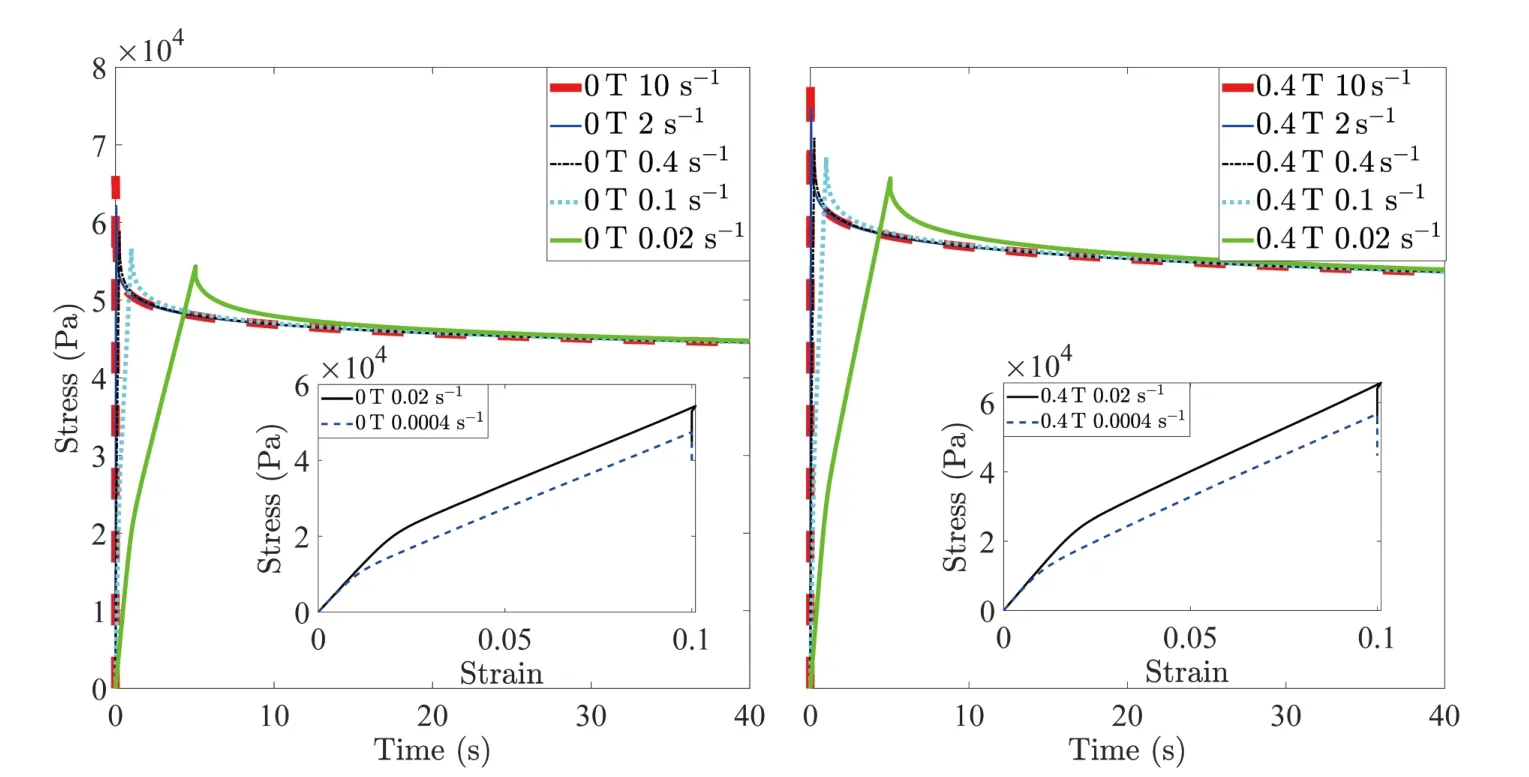
Fig.12. Stress relaxation time history of isotropic MRE with different loading rates and magnetic fields.The inset represents the corresponding stress-strain results.

Regarding the second set of model predictions,isotropic MRE are loaded with triangular strain with different amplitudes (5%,10%,and 15%).Two strain rates,0.0005 and 0.5 s-1,are considered.Regarding the magnetic field,0 and 0.4 T are applied.The stress-strain results are shown in Fig.13.By comparing the area enclosed through the stress-strain curve,it is found that a faster loading rate leads to a larger peak stress and energy dissipation.Furthermore,due to the nonlinearity,the peak stress does not increase proportionally to the strain amplitude.Specifically,the peak stress at 5%,10%,and 15% with a loading rate of 0.5 s-1and magnetic field of 0.4 T are 5.6022×104,8.0628×104,and 1.07591×105N,respectively.Theoretically,this phenomenon is caused by the strain amplitude-dependent viscosity evolution law utilized in Eq.(33).

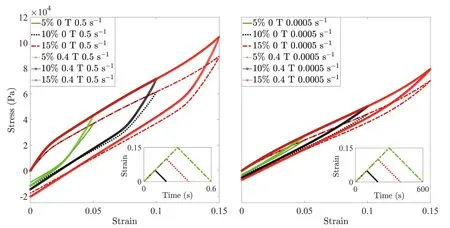
Fig.13. Stress-strain results of isotropic MRE under impact loading with different strain amplitudes and magnetic fields.The inset represents the time-strain impact loading settings.

6 Conclusions

In this work,a constitutive model based on continuum mechanics theory to depict the modulus magnetic stiffening and the magnetic-dependent nonlinear dynamic behavior of isotropic MRE is developed.Specifically,a multiplicatively typed magnetohyperelastic free energy and a strain amplitudedependent viscosity evolution law are proposed.Subsequently,the boundary problem solution and the corresponding numerical implementation method are developed as well.After parameter identification,a comparison between the experimental and simulation results is conducted,and it is shown that the proposed model can depict the modulus magnetic stiffening effect and the magnetic-dependent nonlinear dynamic behavior of isotropic MRE with accuracy.The model developed in this manuscript can be used to promote the design and evaluation of MRE-based devices.

Based on the model developed in this work,many paths are still open for future research.Practically,anisotropic MRE has a more pronounced modulus magnetic stiffening effect than isotropic MRE.For example,the extension of the current model for isotropic MRE can be extended to anisotropic cases to analyze the MRE performance of anisotropic MRE.Furthermore,the current model can be implemented in commercial finite element software such as ABAQUS through a user element (UEL) to predict the magnetomechanical performance of MRE-based devices.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (12102424,12202434,and 11972343),the Anhui Key R&D Program of China (202104a5020009),the Fundamental Research Funds for the Central Universities(WK2090000030),and the Fellowship of China Postdoctoral Science Foundation (2022M713045).

Conflict of interest

The authors declare that they have no conflict of interest.

Biographies

Bochao Wangis currently a postdoctor at the University of Science and Technology of China.He received his Ph.D.degree at the KTH Royal Institute of Technology.His research interests include constitutive modeling of smart materials,application of smart materials in vibration control,and multifield finite element implementation.

Xinglong Gongis currently a Professor at the University of Science and Technology of China.His research interests include the fabrication,characterization,and application of smart materials,advanced measurement methods and applications of experimental mechanics,and the fabrication and application of thermal protection materials.