Thermodynamic geometry of the RN-AdS black hole and non-local observables
Chao Wang ,Bin Wu ,Zhen-Ming Xu and Wen-Li Yang
1 Institute of Physics,Shaanxi University of Technology,Hanzhong 723000,China
2 School of Physics,Northwest University,Xi’an 710127,China
3 Institute of Modern Physics,Northwest University,Xi’an 710127,China
4 Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China
5 Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China
Abstract This paper studies the thermodynamic geometry of the Reissner–Nordstr?m-anti-de Sitter (RNAdS)black hole via detection of the non-local observables in the dual field theory,including the entanglement entropy and equal-time two-point correlation function.With the dimensional analysis,we construct the principle of corresponding states of black hole thermodynamics.As a result,our findings can be applied to black holes with different AdS backgrounds.In this sense,the probe of the thermodynamic geometry of the RN-AdS black hole though the non-local observables in dual field theory has been confirmed numerically.
Keywords: black hole thermodynamic,thermodynamic geometry,phase transition,non-local observables
1.Introduction
The pioneering work by Hawking and Bekenstein on black hole temperature and entropy [1,2] made people realize that black holes are thermodynamic systems that exhibit phase transition behavior.The first black hole phase transition is the Hawking–Page phase transition [3],which is related to the confinement/deconfinement phase transition [4] in the dual field theory,and makes the anti-de Sitter (AdS) spacetime more charming.Next,the discovery of the van der Waals-like phase transition in charged AdS black holes [5] implied that the black hole will undergo second-order and first-order phase transition successively before it reaches the stable phase,which revealed the connection between black holes and ordinary thermodynamic systems.
By treating the negative cosmological constant Λ=?(d ?1)(d ?2)/l2as the thermodynamic pressure P=?Λ/8πG [6–8],the extended phase space of the AdS black hole is established,in which the van der Waals-like phase transition was reconstructed [9].Within this framework,the phase transition and critical behavior of black holes have been extensively studied in [10–18].However,due to the importance of the AdS black hole in the AdS/conformal field theory (AdS/CFT) duality,which describes the fact that the correspondence between quantum gravity and gauge field theory resides on the boundary [19,20],the holographic interpretations of the variation of Λ have received significant attention.
Several works in [21–23] have proposed that the variation of Λ corresponds to varying the number of color N:alternatively,the number of degrees of freedom N2of the dual field theory.In CFT,the number of degrees of freedom is denoted by the central charge with C=ld?2/Gd[24–26],where Gdis the Newtonian constant in d-dimensional spacetime.Therefore,the change in Λ corresponds to varying the central charge in CFT.In a fixed CFT,it is suggested that the central charge C should be constant[27].Recently,Visser derived the holographic thermodynamics in the dual field theory by applying the central charge as a thermal variable,which plays a similar role to the particle number in the thermodynamic system[28].Inspired by this,considerable work has been carried out to reveal the properties of the dual field theory in this context [27,29,30].Going a step further,in [31–35],by fixing the AdS radius l,the extensive black hole thermodynamics have been developed.
While the development of black hole thermodynamics is in full swing,considerable interest has been paid to probing their thermodynamic behavior.To address this,holographic entanglement entropy (HEE) [36,37] in the dual field theory was employed to investigate the detection of the thermodynamic behavior of the Reissner–Nordstr?m-anti-de Sitter(RN-AdS) black hole in [38].The results demonstrated the existence of oscillating behavior in the temperature–HEE plane,resembling the van der Waals phase transition.Furthermore,the critical behavior and the Maxwell equal area law[39,40]were examined and found to be fulfilled.Further study suggested that the oscillating behavior was also observed in the coordinate space organized by the Hawking temperature and geodesic length on the AdS boundary,which is related to the equal-time two-point correlation function and Wilson loop [41,42].
The phase transition in classical thermodynamics originates from intermolecular interaction,but the microstructure of black holes is still a mystery.The introduction of the Ruppeiner geometry [43–45]provides some insight into that.By considering the fluctuation theory,line elements are proposed to measure the distance between fluctuation states,which take the form of
Here,S is the entropy of the system,and Xμare the thermodynamic coordinates depending on the choice of the thermodynamic potential.The curvature scalar calculated from equation(1)describes the interaction within the system.Specifically,a positive(negative)value of the curvature scalar indicates a repulsive (attractive) interaction within the black hole domain,and the noninteracting system corresponding to the flat Ruppeiner metric [46–58].In this sense,the application of the Ruppeiner geometry is the reverse process of statistical physics,i.e.detecting the microstructure of a system with its thermodynamic behavior.It has also been observed that the divergent point of the curvature scalar corresponds to the phase transition point [59],which implied the phase structure will be exposed by the curvature scalar.In[60],the author constructed a new formalism of thermodynamic geometry(NTG)by changing the coordinates of the Ruppeiner metric equation (1) using Jacobian matrices.Therefore,the line element turns to
Considering that the non-local variables have the same oscillating behavior as the black hole phase transition,it is natural to ask whether the information of the underlying microstructure depicted by the thermodynamic geometry can be read in a given CFT.Inspired by this,we explore the connection between the black hole entropy and the non-local observables in dual field theory,including the HEE and the equal-time two-point correlation function;the results specified that the observation of the quantities in CFT will expose the information of the black hole phase structure and thermodynamic geometry.
The outline of this paper is as follows.In section 2,we review the phase structure and the thermodynamic geometry of the RN-AdS black hole.The numerical results to describe the thermodynamic geometry of the RN-AdS black hole with the HEE and two-point correlation function will be investigated in section 3.We end this paper with a conclusion in section 4.Throughout this paper,we adopt the units ?=c=kB=G=1 for convenience.
2.RN-AdS black hole
The RN-AdS black hole in four-dimensional spacetime is characterized by the action in the form of
where l is the AdS radius,and the equation of motion is
The metric function f(r) can be obtained easily
The parameters M and Q in the metric function are the mass and charge of the black hole,respectively.The temperature and entropy are given by
where rhis the position of the outer event horizon.The mass of the black hole can be deduced with the condition f(rh)=0
where Φ=Q/rhis the electric potential difference between the horizon and infinity.
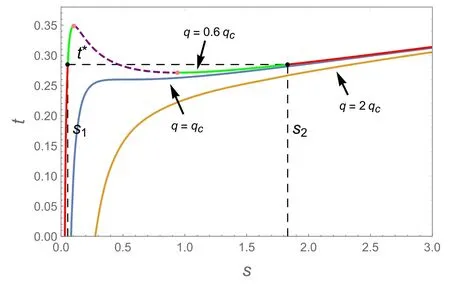
Figure 1.The iso-q curves in {t,s} coordinate space.Here,we set q=0.6qc,qc and 2qc from top to bottom.The Maxwell equal area law is constructed by the black dashed line.
In classical thermodynamics,the critical point of a van der Waals fluid is denoted by the model parameters,and the equation of state with reduced parameters is applicable for the system with different components,which is called the principle of corresponding states.In an AdS background,the cosmological constant plays the role of model parameter as that of van der Waals fluids.Consequently,by considering the dimensional analysis of the thermodynamic variables,the dimensionless thermal parameters are introduced as
In this way,the equation of state with the dimensionless parameters will hold for charged black holes in different AdS backgrounds,which is the law of corresponding states.The equation of state can be redefined as follows
in which the AdS radius l can be set as an arbitrary constant.The critical point decided byis marked as
It is clear that the critical point is universal for the black hole in different AdS spacetime.After obtaining the principle of corresponding states,we would like to depict the van der Waals-like phase transition of the RN-AdS black hole.Based on equation (9),the iso-q process is shown in figure 1.
In the figure,the charge was set as q=0.6qc,qcand 2qcfrom top to bottom.The box formed by the black dashed line corresponds to the Maxwell equal area law of the van der Waals-like phase transition,which implies that the area under the curve between the black dots is equal to the area under the dashed black line.The coexistence temperature t*and s1,2are the coordinates of the box vertices dividing the stable state from the metastable state,which can be obtained as
While the charge is less than qc,the iso-q curve exhibits similar oscillatory behavior to that of the van der Waals phase transition.According to thermodynamic theory,a small stable state will directly transform into a large stable one when the temperature of the black hole exceeds t*.Together with the local extremal point painted in purple,the iso-q curve was divided into five segments.The red solid lines correspond to the small (SBH) and large black holes (LBH),which are thermodynamically stable.The black hole on the purple dashed line is unstable (SBH+LBH).The green solid lines are the metastable curves of the black hole,and they separate the stable and unstable states of the black hole,with the left part being the superheated SBH (SHSBH),while the right part corresponds to the supercooled LBH (SCLBH).As the charge reaches the critical value,these two local extremal points merge into one at the inflection point on the orange curve in figure 1.Upon further increasing the value of q,the curve is monotonic,and the black hole is in the supercritical phase (SCBH).
To reveal the information of the underlying microstructure of the black hole,we adopt the Ruppeiner geometry of the RN-AdS black hole.In the {S,Q} space,from equation(2)with Ξ=M,the thermodynamic metric comes to
Therefore,the thermodynamic curvature scalar arises
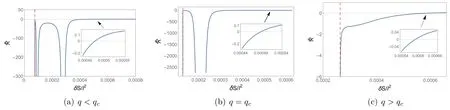
and with the dimension [ R] =1[l]2we combine the equations in equations(5)and(6)to demonstrate the variation of the dimensionless curvature scalarin terms of entropy s with q
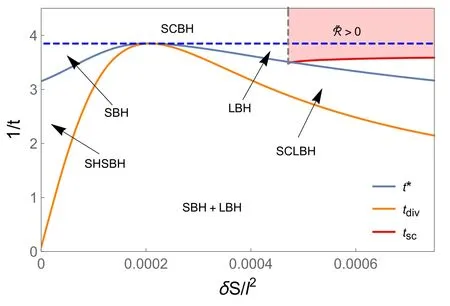
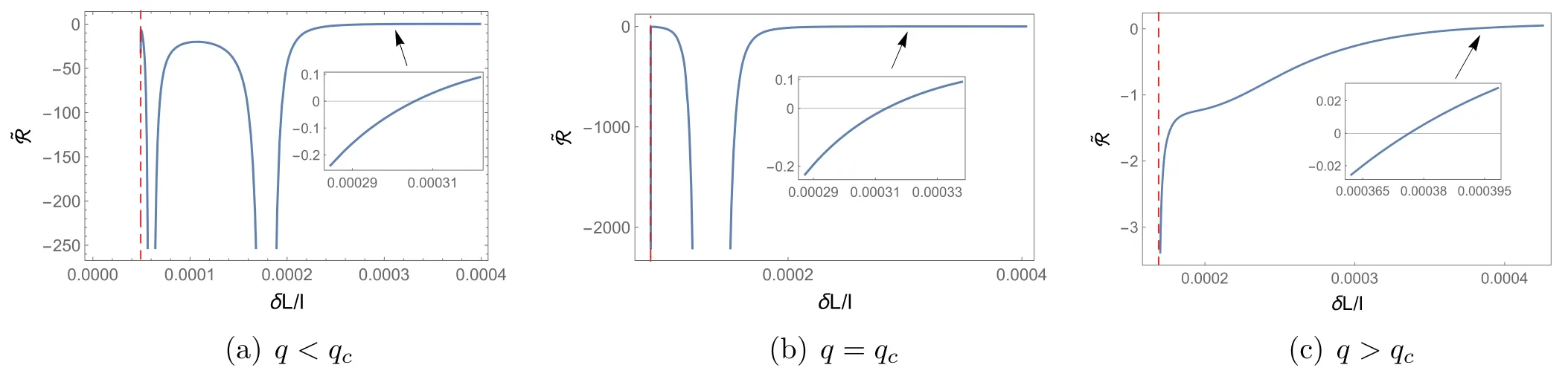
From equation (5),we know that the scalar curvature starts from negative infinity caused by t=0,marked by the red dotted line,which describes the extremal black holes.When q Figure 3.The characteristic curve of scalar curvature in coordinate space{t,s}.The orange and red solid lines are the divergence curve and the variable sign curve of the curvature scalar,respectively.The blue solid line is the coexistence curve in equation (10).The blue dashed curve in the figure corresponds to the critical point temperature. As discussed above,the vanishing point and divergent point ofare helpful for us to learn about the underlying microstructure and the phase structure of the black hole;checking the characteristic curve,which includes the signchanging curve tscand the divergent curvetdiv,of scalar curvature is important.With equations (5),(6) and (12),the characteristic curves can be deduced as which are plotted in figure 3. The blue solid curve in the figure is the coexistence curve based on equations (10) and (11),which is divided into the saturated small phase and saturated large phase using the extreme point.The orange and red curves are the divergence curve and the sign-changing curve of,respectively.The area above the tsccurve that is painted in pink corresponds to the positive value of the curvature scalar,and the interaction is a repulsive domain.Meanwhile,other areas with<0 implied the interaction between the parts of the black hole is an attractive domain.The figure tells us that only the large black hole in low temperatures would show the repulsive interaction.The phase structure was also exhibited in the figure.Above the blue dashed line,the black hole is in the supercritical phase. As we have reviewed the thermodynamic geometry of the RN-AdS black hole,we will further investigate its relation to the non-local observables in a given CFT,including the(HEE) and the two-point correlation function.We would like to start this topic with HEE,which has been proven to show similar oscillation behavior as that of the van der Waals phase transition.In this sense,we will explore whether HEE can reflect the thermodynamic geometry of a black hole. The entanglement entropy (EE) denotes the relationship between two subsystems of a quantum system,which is denoted by A and Ac.When the quantum system lives in a CFT,the EE can be computed by the Ryu-Takayanagi (RT)recipe [36,37] Here,the ΓAis a codimension-2 minimal surface in bulk AdS space that has the same boundary conditions as A on the boundary CFT.According to the metric function equations(4)and(13),the area of the minimal surface ΓAcan be calculated as wherer′=drdθwith θ0as the boundary condition of HEE in the θ direction.Here,L is now introduced as the Lagrangian with θ.The only analytical solution of r(θ) is pure AdS spacetime in the bulk.In the study of HEE,we will solve the equation of motion in ordinary spacetime numerically with the conditions that Figure 4.The dimensionless curvature scalar for the RN-AdS black hole in terms of δS/l2.Here,we set(a)q Notice that for the UV-divergent of the EE,we should regulate it by subtracting the area of the minimal surface in pure AdS,which we denote as δS.When calculating the EE with the RT formula,we ask θ0to be a small value to make sure the minimal surface can return to the subsystem continuously.Therefore,we set θ0=0.1 and the UV-cutoff in CFT with r(0.099).To check whether the HEE can be exploited to reflect the curvature scalar of the black hole,we study the relationship between the Ruppeiner geometry and HEE.The equation for HEE in equation (14) indicated the relation in rhand SA,with which we can establish a one-toone correspondence between the black hole phase transition and the oscillating behavior of non-local observables in the given CFT.The numerical results of the curvature scalar in terms of HEE with different charges is shown in figure 4.The behavior of the curvature scalar with respect to the dimensionless parameter δS/l2with q To show the relation between the thermodynamic properties of the RN-AdS black hole and the HEE,we plot the characteristic curves for the Hawking temperature and EE of CFT in figure 5.The blue dashed line denotes the critical value of t,beyond which the corresponding black hole is undergoing a first-order phase transition.When the temperature is at the critical value,the black hole will show a second-order phase transition.Furthermore,the black hole is in the superficial phase and 1/t exceeds the blue dashed line.The blue solid curve is the coexistence curve,which separates the saturated small and large black hole phases through the critical point.The EE δS with a small or large value indicates that the black hole is thermodynamically stable.The orange curve is the divergent curve of the scalar curvature,which distinguishes the unstable phase from the metastable phase.The red solid curve is the sign-changing curve,and the top area painted in red represents~R >0.Moreover,the correspondence of these characteristic curves between the black hole entropy and HEE announces that the thermodynamic information of the former can be read from the dual field theory. Figure 5.The characteristic curve of the curvature scalar in coordinate space{δS/l2,1/t}.The orange and red solid lines are the divergence curve and sign-changing curve of the curvature scalar,respectively.The blue solid curve is the coexistence curve.The blue dashed curve in the figure corresponds to the critical point temperature. Now,let us focus on the two-point correlation function in CFT.The AdS/CFT correspondence implies that the equaltime two-point correlation function with a large conformal dimension Δ of the scalar operatorO in the dual field theory is holographically approximated as [63] where L is the length between the points(t0,xi)and(t0,xj)on the AdS boundary measured by the metric of the bulk geodesic.Due to the spacetime symmetry,we can let xi=θ,and the boundary is marked as θ0.Therefore,the proper length can be parameterized as Figure 6.The dimensionless curvature scalar for the RN-AdS black hole in terms of δL/l.Here,we set(a)q Figure 7.The characteristic curve of the curvature scalar in coordinate space {δL/l,1/t}.The orange and red solid lines are the divergence curve and the variable sign curve of the curvature scalar,respectively.The blue solid line is the coexistence curve.The blue dashed curve in the figure corresponds to the critical point temperature. where the dot denotest.=drdθ.The equation of motion is obtained from the Euler–Lagrange equation with the LagrangianL with respect to θ.By applying the boundary condition equation (15),r(θ) can be deduced by solving equation (16).We apply the numerical method to calculate the geodesic length,which is difficult to obtain in analytical similarly as long as they are in the same state described by the same dimensionless parameters.By considering the black hole mass,we obtain the thermodynamic scalar curvature equation (12) and show the thermodynamic behavior of the black hole,which implies thatcan be exploited to display the phase transition of the black hole,and the underlying microstructure.We then investigate the thermodynamic geometry of the black hole with the non-local observables in the given CFT.Interestingly,the HEE and equal-time two-point correlation function also show similar behavior in the form.Due to the divergence of the geodesic length at the boundary θ0,it should be regularized by subtracting the geodesic length in pure AdS with the same boundary conditions,denoted as δL.For that purpose,we choose θ0=0.1 and the UV-cutoff in the dual field theory as r(0.099).The relationship betweenand δL/l is shown in figure 6. In this paper,we investigate the probe of the thermodynamic geometry of the RN-AdS black hole by the non-local observables in a given CFT.Through dimensional analysis,we introduce dimensionless thermodynamic variables and establish the corresponding state laws.This principle suggests that charged black holes in different AdS backgrounds behaveplanes,respectively,to the black hole.These results suggest that the HEE and equal-time twopoint correlation function in the given CFT can serve as good probes of the black hole’s thermodynamic geometry. In view of the invisibility of the black hole microstructure,if the holographic form of the thermodynamic geometry is established by the AdS/CFT dual theory,it may disclose the microscopic mechanism of the black hole thermodynamic behavior.We will focus on this issue in our future work. Acknowledgments This work is supported by financial support from the National Natural Science Foundation of China (Grant Nos.12275216,12105222,12247103). ORCID iDs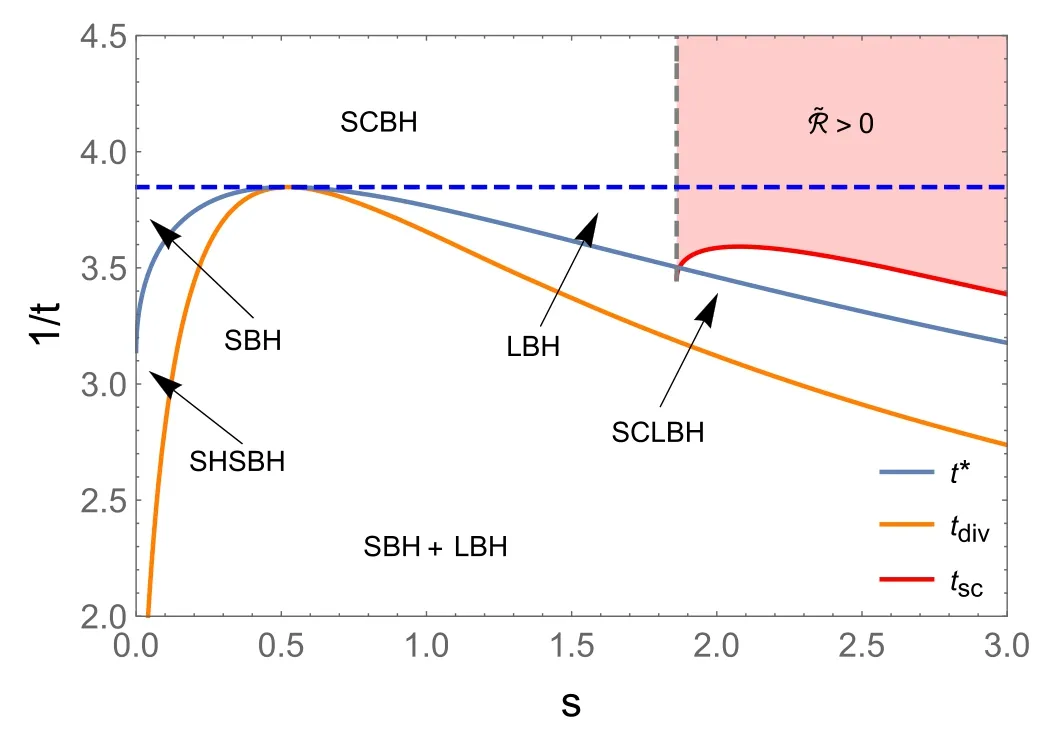
3.Thermodynamic geometry and non-local variables

4.Conclusion
 Communications in Theoretical Physics2024年2期
Communications in Theoretical Physics2024年2期
- Communications in Theoretical Physics的其它文章
- Finite dimensional irreducible representations of Lie superalgebra D (2,1;α)
- Phase diagram of muonium hydride: the significant effect of dimensionality
- Correlation between mechano-electronic features and scattering rates using deformation potential theory
- The size effect and analogous boundary states in a circular non-Hermitian chain
- The modeling non-sequential double ionization of helium atom under highintensity femtosecond laser pulses with shielding charge approximation
- Non-static plane symmetric perfect fluid solutions and Killing symmetries in f(R,T)gravity
