Bulk moduli of two-dimensional Yukawa solids and liquids obtained from periodic compressions
Shaoyu LU (盧少瑜), Dong HUANG (黃棟), A SHAHZAD and Yan FENG (馮巖),3,*
1 Institute of Plasma Physics and Technology, School of Physical Science and Technology, Soochow University, Suzhou 215006, People's Republic of China
2 Department of Physics, Government College University Faisalabad (GCUF), Allama Iqbal Road,Faisalabad 38040, Pakistan
3 National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, People's Republic of China
Abstract Langevin dynamical simulations are performed to determine the bulk modulus in twodimensional (2D) dusty plasmas from uniform periodic radial compressions.The bulk modulus is calculated directly from its physical definition of the ratio of the internal pressure/stress to the volume strain.Under various conditions, the bulk moduli obtained agree with the previous theoretical derivations from completely different approaches.It is found that the bulk moduli of 2D Yukawa solids and liquids are almost independent of the system temperature and the external compressional frequency.
Keywords: bulk modulus, dusty plasma, simulation, Langevin, complex plasma, Yukawa systems
1.Introduction
The bulk elastic property is an important mechanical property of a material or a fluid, which determines its volumetric resistance to a given external pressure[1].To characterize the bulk elastic property, the bulk modulus K, or the modulus of the compression [2], is often used.The bulk modulus is defined as the ratio of the change in the pressure/stress to the resulting decrease of the volume [2], with the equation
Here,P is the pressure of a liquid or the stress of a solid,while V is the volume of the studied material[2].The bulk modulus of a substance determines the inside mechanical wave propagation,so that it can be derived from the sound speed in the studied substance [3, 4], which we will present in detail later.
Dusty plasma, also termed complex plasma, contains four components of electrons, ions, neutrals gas, and micron-sized solid dust particles [5-18].In typical laboratory plasma conditions, dust particles are highly charged to ~-104e in the plasma,so that they are suspended and confined in the sheath by the electric field [19, 20].When the particle number is not extremely large,these dust particles are able to self-organize into a single-layer suspension, typically termed as the two-dimensional (2D) dusty plasma [21, 22].These negatively charged dust particles repel each other through the Yukawa interaction[23],?(r) =Q2exp (π?0r, where r, λD, and Q are the distance between two particles,the screening length,and the particle charge,respectively,so that the theoretical model of the 2D Yukawa system is often used to describe 2D dusty plasmas[24].Since these particles are highly charged, they are strongly coupled [25], i.e.the potential energy between neighboring particles is higher than their average kinetic energy, so that a collection of these dust particles exhibits the typical liquid-like[26-31] or solid-like [32-40] properties.
The bulk moduli of 2D dusty plasmas, or 2D Yukawa systems,have already been theoretically investigated[41-43].In [41, 42], from the obtained equation of state [44] for 2D Yukawa liquids,the bulk moduli and adiabatic bulk moduli of 2D Yukawa liquids are analytically derived,respectively,as a result, they can be easily estimated quantitatively from the system conditions.In[43],an analytical approach is proposed to calculate high-frequency bulk moduli of 2D weakly screened Yukawa fluids and solids, which have a high accuracy rate, mainly in the strongly coupled regime.However,from our literature search in dusty plasmas and Yukawa systems, we have not found any determinations of the bulk modulus from its definition directly.Furthermore, the variation of the bulk modulus as the function of the temperature or the compression conditions,like the compressional frequency and amplitude, is also unknown.Here, we perform simulations to compress 2D Yukawa solids and liquids to determine their bulk moduli directly from the definition, and then compare them to the previous theoretical derivations, as well as investigate their dependence on other conditions.
The rest of this paper is organized as follows.To mimic 2D dusty plasmas under uniform periodic radial compressions, we perform our Langevin dynamical simulations, as described in section 2.In section 3,we briefly review the previous studies of the bulk modulus in dusty plasmas.In section 4, from our simulations, we determine the bulk moduli of 2D Yukawa systems under various conditions using the definition.Our obtained results of the bulk modulus quantitatively agree with the previous results of 2D Yukawa solids and liquids.We also find that,for our studied regimes,the obtained bulk modulus is nearly independent from the system temperature and the compressional frequency.Finally, we give a brief summary.
2.Simulation methods
To mimic 2D dusty plasmas manipulated by uniform periodic radial compressions, we perform Langevin dynamical simulations using LAMMPS [45].All simulated particles are confined by a Gaussian potential well with a free boundary,and the equation of motion for each particle i is
where the four terms on the right-hand side are the interparticle Yukawa repulsion summed with all other particles j,the frictional gas drag [46], the Langevin random kicks [47],and the confinement force, respectively.The confinement force is derived from the Gaussian potential at a circular boundary aswhere R is the radius of the circular region to confine these particles.To apply a uniform periodic radial compression, the confinement force is modified toFconf=where the circular boundary has an oscillating frequency ω and a small amplitude A.
Typically,2D dusty plasmas,or 2D Yukawa systems,are characterized by two dimensionless parameters,which are the coupling parameter Γ=Q2/(4π?0akBT) and the screening parameter κ=a/λD.Here, T, kB, and a are the kinetic temperature of dust,the Boltzmann constant,and the Wigner-Seitz radius, respectively.In addition, the nominal 2D dusty plasma frequencyand the Wigner-Seitz radius a are used to normalize the time and length scales, respectively.It can be noted that, following the tradition of the previous dusty plasma or Yukawa investigations,such as[47],we use the dimensionless parameters of Γ and κ to characterize the studied Yukawa system with the carefully adjusted temporal and spatial scales [29], while the detailed information related to the individual particle can be derived from the specified Γ and κ values.
Here are some details of our simulations.For most simulation data presented in this paper,the system size is specified as R=78a including N=5935 particles.The screening parameter κ is chosen to be 0.5,1.0,and 2.0.For each κ value,the values of Γ cover the typical liquid and solid regimes [48].The frictional gas damping is specified as ν=0.027ωpd, corresponding to a typical value in experiments [29, 31].The integration time step is specifeid as either 7.07 × 10-3for the higher Γ values, or 2.82 ×for the lower Γ values.When the periodic radial compression is applied, we record the positions and velocities of all particles in the temporal duration of tωpd=35000 for the latter data analysis.
The typical initial configurations of a Yukawa solid and a Yukawa liquid in our simulations are presented in figure 1.It is clear from figure 1 that all simulated particles are confined in a circular region by the Gaussian potential well.To induce the periodic radial compression, the position of the Gaussian potential well is shifted periodically with a small amplitude of A,which is specified from 0.25a to 1.0a.For this range of A, the resulting volume strain is only about 0.65%to 2.6%,so that the system is in the pure elastic regime, leading to the accurate determination of the bulk modulus.As a result,we determine the bulk moduli of our studied 2D Yukawa solids and liquids from the definition of the ratio of the pressure/stress change to the resulting volume strain variation using our simulation data.

Figure 1.Typical configurations of a 2D Yukawa solid(a)and a 2D Yukawa liquid(b) in our simulations.
3.Review of bulk modulus in 2D Yukawa systems
Here, we briefly review the previous investigations of the bulk modulus in 2D dusty plasmas in [41, 43].
In [41], using the expression of the pressure from their equation of state [44], the analytical expression of the bulk modulus for 2D Yukawa liquids is directly obtained as equation (6) of [41], which is just
In another approach[43],a few analytical expressions to evaluate elastic moduli of 2D Yukawa systems are proposed.The corresponding derivations are based on the instantaneous elastic moduli of simple (monoatomic) fluids expressed in terms of the pair-interaction potential ?(r) and the radial distribution function(RDF)g(r)[49].From the derivations in[43], in the weakly screening conditions, the instantaneous bulk modulus can be expressed as
which is just equation (11) in [43].Here, x=r/a is the reduced distance.The related series of relations are also presented to simplify the calculation, i.e., equation (13) of[43], as
Here, for the states not too far away from the solid-liquid phase transition, the excess energy uexcan be approximately expressed as uex?MΓ in[43],with the Madelung coefficient M(κ) of the triangular lattice.In this case, the function f0just equals the Madelung coefficient, which can be fitted by the expression of M(κ)=-1.1061+0.5038κ-0.11053κ2+0.00968[50].
The longitudinal and transverse sound speeds are directly related to the elastic moduli of a substance[3,4],for example,the bulk modulus determines the dispersion relation of Yukawa fluids at weak and moderate coupling as studied in[51].For 2D systems,the instantaneous bulk modulus can be expressed as [43, 52, 53]
where m is the mass of one particle, ρ=1/(πa2) is the number density, and CL/Tis the longitudinal/transverse sound speed.Here, we substitute the sound speeds of the perfect 2D Yukawa crystal obtained from [54, 55] into equation (6), and then define the obtained instantaneous bulk modulus value as K0, which in principle is the theoretical estimation of the bulk modulus for the perfect 2D Yukawa crystal.In this paper, we determine the bulk moduli of 2D Yukawa solids/liquids from the definition directly using our Langevin simulation data.We then compare our obtained results to the theoretical derivation of K0and other estimated bulk moduli using the previous theoretical approaches from [41, 43].
4.Results
4.1.Determination of bulk modulus
For 2D systems, the definition of bulk modulus of equation (1) is changed to
where the volume V is replaced by the area S.Here,we obtain the pressure/stress P of 2D Yukawa systems from the diagonal elements of the stress tensor,as in[56,57].We calculate the time series of the two diagonal elements of the stress tensor Pxxand Pyy, divided by the total area, using
and
Due to the isotropy of our simulated system,especially during the compression procedure, we are able to calculate the time series of the pressure P for liquids, or the stress P for solids,using P(t)=(Pxx(t)+Pyy(t))/2.
After uniform periodic radial compressions are applied,we obtain the bulk modulus from the response of the pressure/stress to the volume strain directly, as one typical example is shown in figure 2.The resulting pressure/stress P exhibits a phase difference of π on the volume strain ΔS/S0,as shown in figure 2(a),due to the resistance of the simulated system to the applied uniform compressions.Thus, as shown in figure 2(b), we find that the response relation between P and ΔS/S0is linear,i.e.the response curve almost overlaps in a straight line indicated by a dashed line there.In fact, the slope of this dashed line is just the corresponding bulk modulus K of our simulated system.In figure 2(b), our obtained bulk modulus is K/(Q2/4π?0a3)=0.924 for our simulated 2D Yukawa solid [48] with the conditions of κ=0.5, Γ=800 and ω/ωpd=0.001.

Figure 2.Time series of the pressure/stress P and volume strain ΔS/S0 (a), as well as the corresponding response relation between them(b), under the conditions of κ=0.5, Γ=800, and ω/ωpd=0.001.
Substituting the condition of κ=0.5 into the expressions of the sound speeds in the perfect 2D Yukawa crystal[54],we obtain the corresponding longitudinal and transverse sound speeds of CL=1.23aωpdand CT=0.25aωpd, respectively.Combining these sound speeds into equation (6), we obtain the theoretical bulk modulus of the corresponding perfect 2D Yukawa crystal as K0/(Q2/4π?0a3)=0.92.Thus, our obtained bulk modulus of K/(Q2/4π?0a3)=0.924 for the 2D Yukawa solid above well agrees with the theoretical derivation of K0of the same κ value, with only about ≤0.5%uncertainty, further suggesting that our simulation methods are reliable and the obtained result is sufficiently accurate.It can be noted that, for all data presented in this paper, if not specified, the default values of the simulated particle number and volume strain are chosen as N=5935 and ΔS/S0=0.0065, respectively.
4.2.Comparison to previous studies
We compare our obtained results of the bulk modulus to the previous theoretical estimations in [41, 43], as shown in figure 3(a).Here, for the comparison’s convenience, the bulk modulus K is always normalized by the corresponding value of K0, i.e.the theoretical estimation of the bulk modulus for the perfect 2D Yukawa crystal with the corresponding κ value.We also normalize the coupling parameter Γ using the corresponding melting point of the 2D Yukawa system Γm[48], which also varies with κ.From figure 3(a), it is clear that, for each κ value, our obtained bulk modulus from our simulation data well agrees with K0, in both the solid and liquid regimes.In the liquid regime, we substitute our simulation conditions of κ and Γ into equation (6) of [41], to obtain the estimations of the bulk modulus under the corresponding conditions.Clearly, for κ=0.5 and 1.0, the estimation results from equation (6) of [41] are about 20%higher than our simulation results from the periodic compressions, while for κ=2.0, the estimation is about 20%lower.From our understanding, this difference probably is induced by the fitting uncertainties ofα′ andβ′, which are further magnified in the derivative of the internal pressure to obtain the bulk modulus [41].
For another approach proposed in [43], which is said to be more accurate in the more strongly coupled regime,i.e.for either solids or liquids only near the melting point, the corresponding estimation results are also presented in figure 3(a).By substituting the values of κ and Γ used in our simulations and those equations presented in [43] into equation (11) of [43], we obtain estimations of the bulk modulus.It is found that, for each κ value, the obtained estimations of the bulk modulus from [43] are always larger than our results within ≈15%, as shown in figure 3(a).It seems that this ≈15% difference comes from the magnification of the fitting expressions in [43], similar to the previous comparison with [41] above.It can be noted that, although this difference is slightly lower than the above comparison with [41], the estimation procedure is much more complicated.In addition, from the estimation results from [43] in figure 3(a), the bulk modulus increases slightly with the temperature, and this trend is barely exhibited in the results from [41].

Figure 3.Comparison of our determined bulk moduli to the estimations from various theoretical approaches(a), and the dependence of the bulk modulus on various conditions of the compressional frequency, system size, as well as the volume strain amplitude(b).The coupling parameter Γ is normalized by Γm, the corresponding melting point of 2D Yukawa systems [48].
4.3.Dependence of bulk modulus on temperature and frequency
As the major result of this paper, we investigate the dependence of the bulk modulus in 2D Yukawa systems on various conditions, as shown in figure 3.In figure 3(a), for various κ values, we find that the normalized bulk modulus values all fluctuate very briefly around unity, agreeing with the theoretical value of K0within only ≈2%variation,for our studied Γ range.That is to say, for our studied conditions here,the temperature does not have a significant effect on the magnitude of the bulk modulus for 2D Yukawa solids and liquids.The observed variation trend of the bulk modulus with the temperature is closer to the results in[41],while it is slightly different from the results in [43].
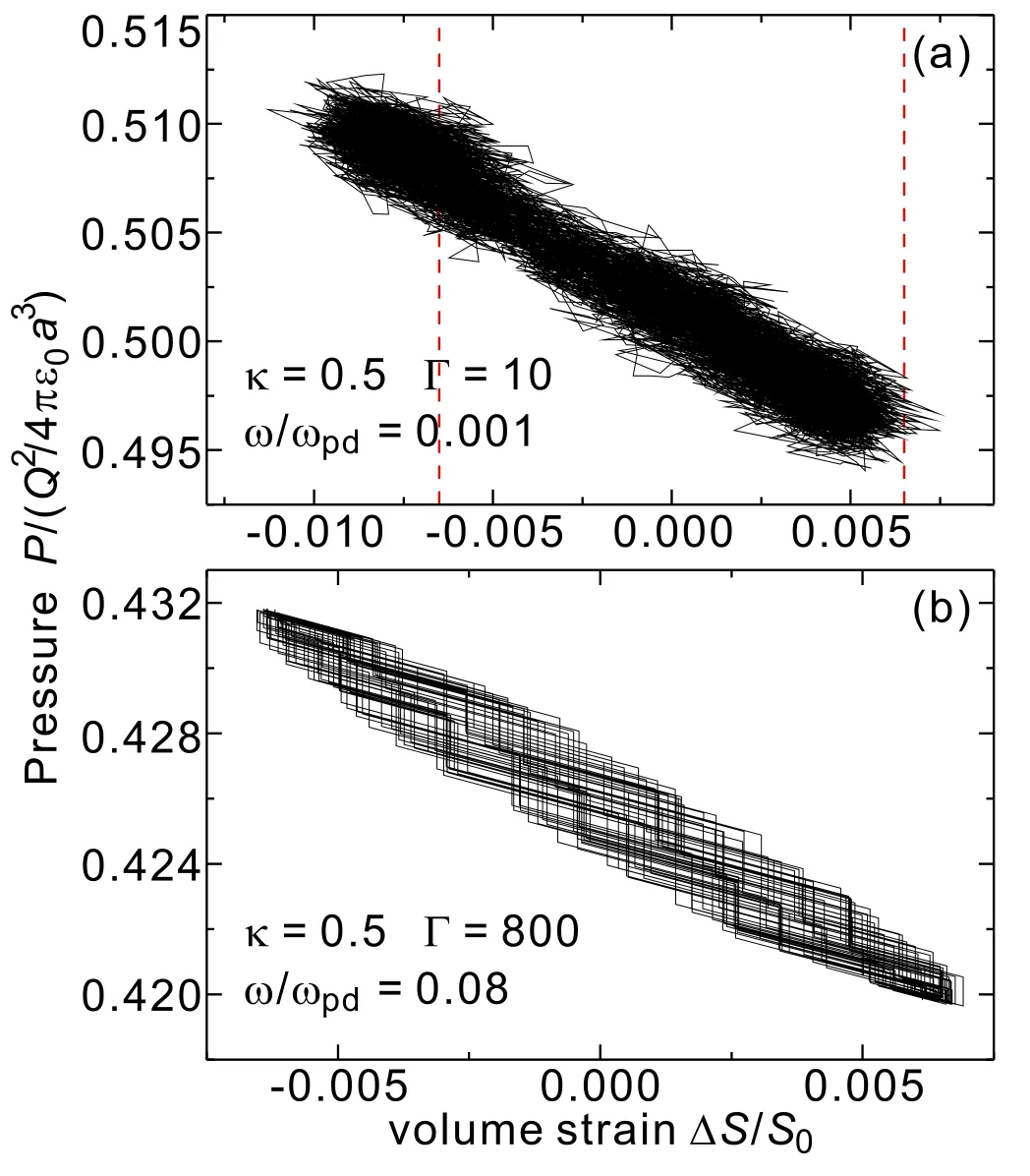
Figure 4.Two typical examples of the nonlinear response between the pressure/stress P and the volume strain ΔS/S0,due to the higher temperature(a) and the higher compressional frequency(b).
To investigate the dependence of the bulk modulus on the frequency,we also vary the compressional frequency from 0.001 to 0.04ωpdfor the conditions of κ=0.5 and Γ=800,as shown in figure 3(b).It is found that,within our studied compressional frequency range, the normalized bulk modulus essentially remains unchanged.The difference between K0and our obtained bulk moduli from the periodic compressions is less than 1%.In addition, we also perform a few simulation runs with various values of the system size and the volume strain magnitude, as shown in figure 3(b).Clearly,from figure 3(b),we confirm that neither the system size nor the magnitude of volume strain has a significant effect on the obtained value of the bulk modulus for 2D Yukawa systems.From all these results, it seems that the bulk moduli of 2D Yukawa solids and liquids are always very close to the bulk modulus of the perfect crystal K0, which only depends on the screening parameter κ, however, other conditions are not able to modify them significantly.
4.4.Limitations of our simulation methods
Our simulation methods also contain some limitations; two typical examples are presented in figure 4.As shown in figure 4(a),for the lower Γ value,i.e.the higher temperature,the response curve between the pressure/stress P and the volume strain ΔS/S0is expanded to a much wider region, due to the large thermal fluctuation, or the enhanced thermal motion of particles.Then the fitting straight line between the pressure/stress P and the volume strain ΔS/S0definitely contains substantial errors.In fact,in this case,the compressional ratio even exceeds the specified volume strain amplitude,as the left portion beyond the left dashed line as indicated in figure 4(a).
Similarly, for a higher frequency of the periodic compression, the expected linear response of P and ΔS/S0is also broken, as shown in figure 4(b).Clearly, in this case, the response curve exhibits a successive ladder-like feature.We speculate that this nonlinear response may be related to the response time of the particle motion to the moving confinement potential well.When the applied frequency is too high, the response of the particle motion cannot be perfectly synchronized, so that the response curve always exhibits this ladderlike feature.In fact,for the lower compressional frequencies in our reported data above,although the response of P and ΔS/S0is also not very smooth,this ladder-like feature is negligible,so that the linear fitting method can be accurately used to determine the bulk modulus, as shown in figure 2.However, for figure 4(b), the linear fitting definitely contains much larger errors.As aforementioned, the limitations of our simulation methods mainly prevent us from determining the bulk modulus at higher temperatures and under higher compressional frequencies.When the compressional frequency is too high, our method to directly determine bulk modulus from its definition is not accurate anymore,so that a different approach should be used to determine the bulk modulus, for example, using the expression that combines the interaction potential and the radial distribution function to estimate the instantaneous elastic moduli in [43], which is well beyond the scope of this paper.
5.Summary
In summary, we perform Langevin dynamical simulations to study bulk moduli of 2D dusty plasmas by applying uniform periodic radial compressions.From the definition of the bulk modulus,which is the ratio of the pressure/stress to the volume strain, we determine the bulk modulus and then investigate its dependence on various conditions.We compare our obtained bulk moduli to the previous theoretical estimations from various approaches, and find that our obtained bulk moduli agree with these estimations.We also find that, for our studied conditions,the bulk modulus almost remains unchanged for 2D Yukawa solids and liquids.None of the compressional frequency, the system size, and the volume strain amplitude has a significant effect on the magnitude of the bulk modulus for 2D dusty plasmas or 2D Yukawa systems.In addition, we also list the limitations in our simulation methods, leading to the inaccurate determination of the bulk modulus at higher temperatures and under higher compressional frequencies.
Acknowledgments
This work was supported by National Natural Science Foundation of China (Nos.12175159 and 11875199), the 1000 Youth Talents Plan, startup funds from Soochow University, and the Priority Academic Program Development(PAPD) of Jiangsu Higher Education Institutions.
 Plasma Science and Technology2023年3期
Plasma Science and Technology2023年3期
- Plasma Science and Technology的其它文章
- Application of integrated simulation environment SIEMNED to the analysis of the MEPHIST-0 tokamak operation
- Improvement of a temperature response function for divertor heat flux monitoring in fusion devices
- Degradation of sulfamethoxazole in water by dielectric barrier discharge plasma jet:influencing parameters, degradation pathway, toxicity evaluation
- Experimental investigation of dynamic stall flow control using a microsecond-pulsed plasma actuator
- Laser-assisted ablation and plasma formation of titanium explored by LIBS,QCM, optical microscopy and SEM analyses along with mechanical modifications under different pressures of Ar and Ne
- Study on the effect of focal position change on the expansion velocity and propagation mechanism of plasma generated by millisecond pulsed laser-induced fused silica
