Effect of porous surface layer on wave propagation in elastic cylinder immersed in fluid

Na-Na Su(蘇娜娜), Qing-Bang Han(韓慶邦), Ming-Lei Shan(單鳴雷), and Cheng Yin(殷澄)

College of Internet of Things Engineering,Hohai University,Changzhou 213022,China

Keywords: wave propagation,porous surface layer,dispersion,attenuation

1. Introduction

There has been a broad interest in acoustic waves propagating in cylindrical structure, such as cylinder, pipe, and borehole due to its essential applications in various technical and engineering processes. The study of wave propagation of the cylindrical rods immersed in fluid is a topic of great importance in engineering, geophysics, and medicine.The guided wave propagations in fluid-loaded rods were studied, and the opposite effects of fluid loading on the velocity of dilatational waves in thin plates and rods through experiments were verified.[1–4]The guided waves in a transversely isotropic cylinder immersed in fluid were analyzed.[5–7]Recently,wave propagation in the sandwich cylinder has received more and more attention. Dutrion and Simon examined the property of acoustic scattering with device, an infinite rigid cylinder with multilayer wrapping made of viscoelastic material placed in fluid.[8]Akbarovet al.[9]and Liet al.[10]studied the axisymmetric longitudinal fundamental wave propagation(dispersion)in the bi-layered circular cylinder made of linear viscoelastic materials and extended the classical wave propagation theory in elastic cylinders. Talebitootiet al. determined the sound transmission loss of an infinitely long composite cylinder, and inspected the effects of various material cores on the sound insulation property of the doubly curved shells.[11,12]

Previous researches clearly show that although many researchers have investigated the acoustic propagation properties of various infinitely long sandwich structures including the plate and cylinder, most of the theoretical researches considered the clad structures consisting of an isotropic or anisotropic core and an arbitrary number of single-phase wrappings. As is well known, in the materials such as concrete columns have internal damping present within their structure.Besides,hydrogeological studies also indicate that the surface material of the cylinder has a certain complexity,and the shallow surface of the material is highly porous. Hence, it is impractical to apply the single-phase medium directly to modelling. Owing to the fact that the porous medium is taken into account in both solid matrix and pore fluid, modelling the porous medium as a surface wrapping layer of an elastic cylinder can present more realistic, accurate, and reliable results. The research on acoustic propagation in the cylindrical structures with the porous material sandwich is necessary and meaningful. However, the acoustic propagation of a cylinder wrapped with a porous material layer has not been thoroughly investigated yet. For instance, as one of the few researches in this field,a cylinder interlayered with porous materials and excited by pressure fluctuation has been studied by Zhouet al.,[13]which involves some disadvantages. In the present study, the porous material is replaced by an equivalent fluid.As another consequence,Gohariet al. considered neither the diversity of the structure nor the effect of the porous parameters on the structural response.[14]As an extension and supplement,we model the porous material as a surface wrapping layer of an infinitely long cylinder.

In this work,the wave propagation in the elastic cylinder wrapped with a porous medium immersed in fluid is studied.Frequency equations of flexural modes each for a pervious surface and an impervious surface are obtained by employing Biot theory of wave propagation in fluid saturated porous solid. The degenerate cases of the general frequency equations,where both the wavenumberkand circumferential numbernare zero, are considered. The reliability of the results can be validated by reducing the porosity or thickness of the porous medium wrapping layer. By ignoring the pore fluid effects, the purely elastic cylinder immersed in fluid is obtained as a particular case.Finally,the influences of the porous medium wrapping layer’s porosity, thickness, and static permeability on the phase velocity and attenuation of longitudinal and flexural modes for pervious surface are discussed.The rest of this paper is organized as follows. The geometric model,boundary conditions and dispersion equations of the problem are presented in Section 2. Numerical results are then discussed in Section 3 and conclusions are given in Section 4.

2. Basic equations and problem formulation

2.1. Geometric model

This section presents the mathematical formulations for the guided waves propagating in the elastic cylinder wrapped with a porous medium immersed in fluid. Theoretical model and a cylindrical coordinate system are established and shown in Fig.1,where origin is atoand cylinder symmetrical axis isz, the directionsrandθare in the plane of the cross section.Assume that the outer radius isbalong the radial direction,aindicates the radius of the elastic cylinder, and the porous medium’s thickness ish=b-a. Here,three sets of subscripts are adopted to identify more parameter properties. The first set of subscripts E,P,F,S,and L represent the elastic cylinder,porous medium,fluid,skeleton material,and pore fluid material that compose porous medium,respectively;the second set of subscripts “l(fā)” and “t” denote longitudinal wave and transverse wave, respectively; the third set of subscripts “f” and“s”refer to fast longitudinal wave and slow longitudinal wave in porous medium;cEl,cEt, andρErepresent the longitudinal wave velocity,transverse wave velocity,and density of the internal elastic cylinder, respectively;cPlf,cPls, andcPtdenote the fast longitudinal,slow longitudinal,and shear wave velocity in porous medium; the parametersρSandρLdenote the density of the porous medium’s solid skeleton and pore fluid,respectively,whilecFlandρFrepresent the longitudinal wave velocity and density of the surrounding fluid.

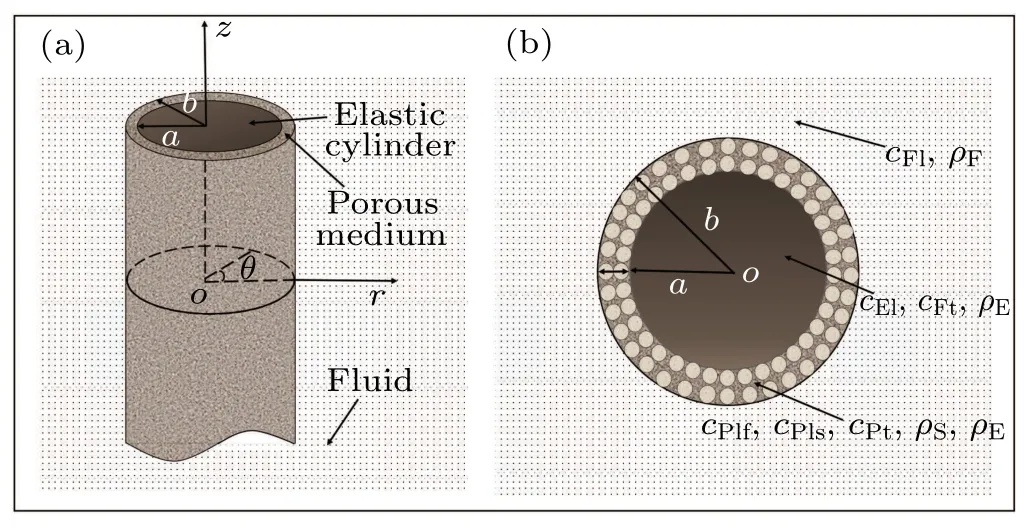
Fig.1. (a) Side view and (b) plan view of elastic cylinder wrapped with porous medium immersed in fluid.

2.2. Governing differential equations and wave solutions

A symmetrical geometric model(Fig.1)is constructed to derive the dispersion equation. The media in the model are considered to be homogeneous and isotropic. In this subsection, we provide in detail the process used to derive the dispersion equations and cutoff frequency equations of flexural modes each for a pervious and an impervious surface in an elastic cylinder wrapped with a porous medium immersed in fluid.

According to Biot’s theory,[15,16]in the presence of dissipationb,the equations of motion of a macroscopically homogeneous,isotropic,fluid saturated porous medium are

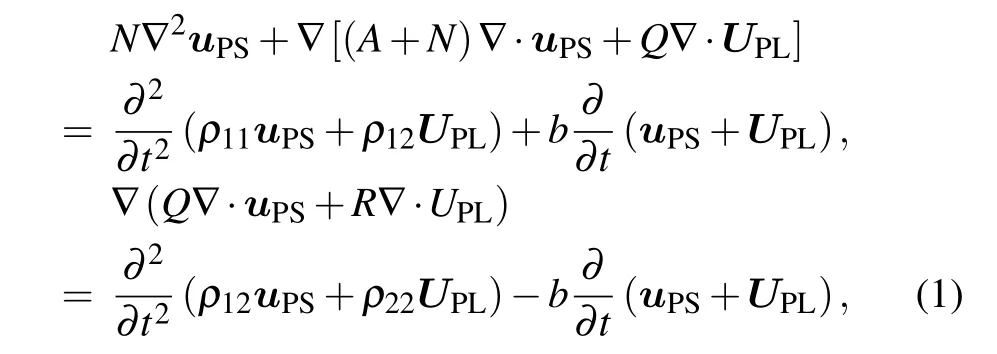
whereuPS=(urPS,uθPS,uzPS)andUPL=(UrPL,UθPL,UzPL)are the displacement of solid and the displacement of pore fluid, respectively;A,N,Q, andRare all porous constants,[17,18]specifically,AandNcorrespond to the familiar Lame constants of a purely elastic solid, andNalso represents the shear modulus of the solid,Qis a measure of the coupling between the volume change of the solid and that of the pore fluid, andRis the measure of the pressure which must be exerted on the fluid to force a given volume of it into the aggregate with the total volume remaining constant; parametersρ11,ρ12, andρ22are the dynamic coefficients that take into account the inertia effect of the moving fluid:ρ12is a coupling coefficient which represents a measure of the force which must be exerted on the pore fluid to prevent its(average)motion when an acceleration is imparted to the solid surrounding it.

A flexural mode in which all three components of the displacement exist and depend on the angleθ. The resolution of each of the displacements in Eq. (1) into a dilatational scalar potential and an equivoluminal vector potential:

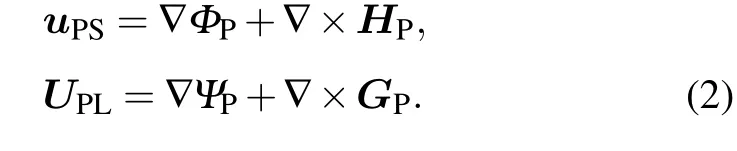
EliminatingΨP, the resulting equation governingΦPcan be derived as

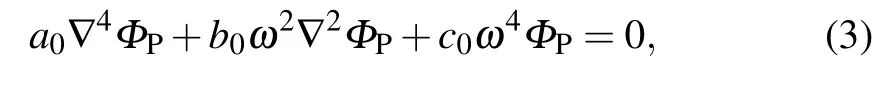
where

and they are non-negative.

In a porous medium, the solutions of Eq.(3)correspond to the two dilatational waves,often referred to as the fast longitudinal wave and slow longitudinal wave,respectively. The solution of Eq.(3)can be written as

and the solution of Eq.(1)corresponds to the shear wave and is given by

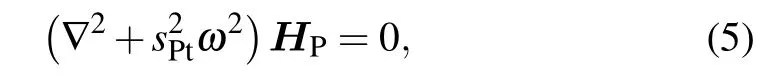
where

The solutions correspond to the two longitudinal waves, the wave corresponding toΦP1being the fast longitudinal wave,propagating with a phase velocity,that corresponds toΦP2being the slow longitudinal wave,whose phase velocity iss-1Pls,andis the phase velocity of the shear wave.

The fast longitudinal and slow longitudinal waves propagating in the porous medium can be expressed as

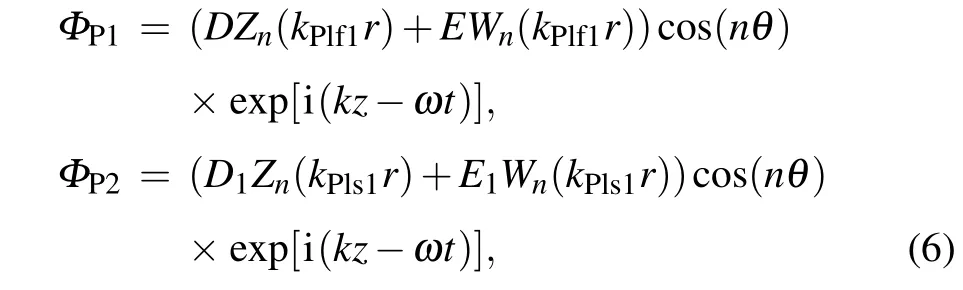
and the shear wave propagating in the porous medium(HP=(HPr,HPθ,HPz))is

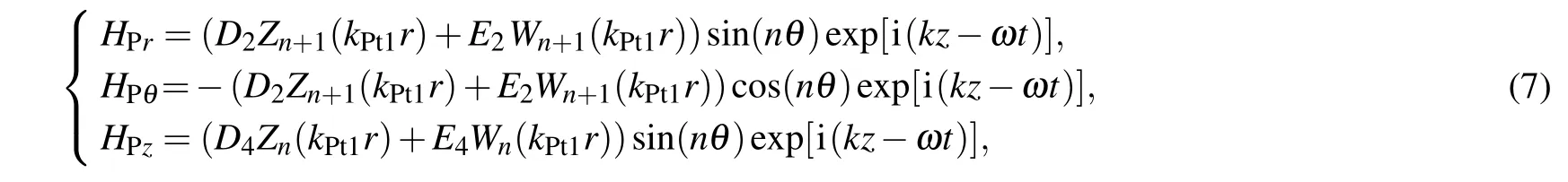
whereD,E,D1,E1,D2,E2,D4,E4are the undetermined coefficients;nis the circumferential number;i is complex unity or i2=-1;kis the wave number;ωis the circular frequency;

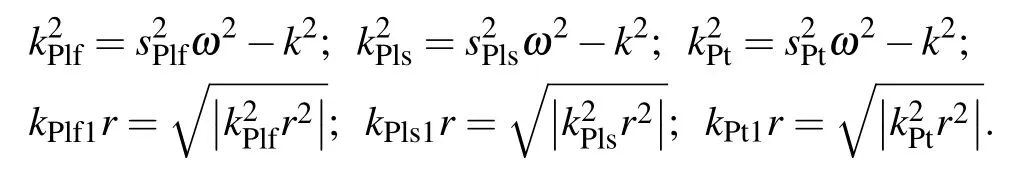
For brevity,Zdenotes aJorIfunction, andWrepresents aYorKfunction according to Table 1,[19–21]which further refines and improves the interval division in Ref.[21]and fully reflects the role of porosity.

With regard to the fluid phase in a porous medium, the equation consists of two parts, namely the longitudinal wave potentialΨPand the shear wave potential,i.e.

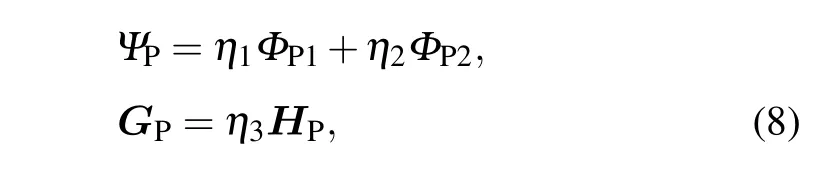
whereGP=(GPr,GPθ,GPz);η1,η2,andη3are the participation coefficients of the fast longitudinal wave,slow longitudinal wave,and shear wave,respectively.[22,23]

Table 1. Bessel functions used at different intervals of frequency ω.

Similarly,the solutions of the flexural mode propagating the elastic medium cylinder are given as follows:

By substituting the expression of the displacement vector into the fluid pressure and radial displacement equation of motion for an inviscid fluid,we can express the fluid pressure as

2.3. Boundary conditions and frequency equations

For perfect contact between the porous cylindrical wrapping and fluid,the normal stresses and radial displacements are continuous. At inner boundary (r=a),[24–26]the boundary conditions of flexural modes for an elastic cylinder wrapped with a porous medium immersed in fluid are

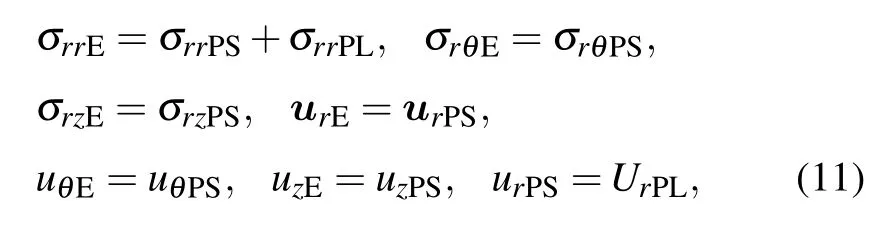
and the outer boundary(r=b)are

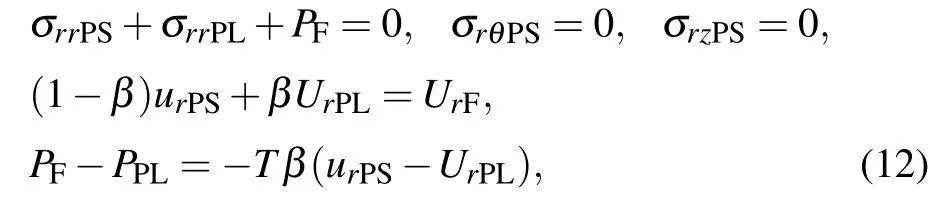
whereβis the porosity;uθEanduzEare the shearing displacement of the elastic cylinder;PPL=-(σrrPL/β) is the fluid pressure in the pore space;Tis a kind of surface flow impedance,[27,28]which can be used to model permeability discontinuity effects such as the mudcake and impairment layers.[29,30]Two special limiting cases that will be considered are: (i)T=0 (i.e.PF=PPL) corresponding to an open pore situation with free flow of fluid in and out of pores, and(ii)T=∞corresponding to a sealed pore situation. SincePF,andPPLare finite,T=∞impliesurPS=UrPL,and thus there is no relative flow.

Substituting Eqs. (8)–(10) into the boundary conditions(11)and(12)results in a system of twelve homogeneous algebraic equations containing twelve constantsB,C,C1,C3,D,D1,D2,D4,E,E1,E2,andE4.For a non-trivial solution,the determinant of the coefficients must vanish. Eliminating these constants yields the frequency equation of flexural modes of an elastic cylinder wrapped with a porous medium immersed in fluid in the case of a pervious surface(T=0)to be

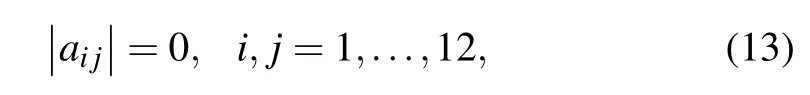
where the matrix elementsaijare given in Appendix A.

Similarly,the frequency equation in the case of an impervious surface(T=∞)is

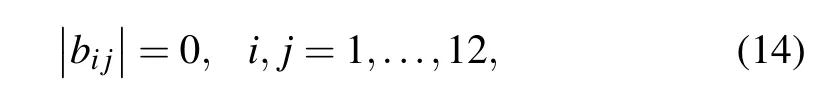
where the elementsbijare defined in Appendix B.

2.4. Cutoff frequencies

The frequencies obtained by equating the wavenumber to zero are the cutoff frequencies. For wavenumberk=0,i.e.by considering zeroth azimuthal mode,the frequency equation of a pervious surface Eq.(13)reduces to the product of two determinants as

whereL1andL2are given in Appendix C.The equationL1=0 depends on the elastic cylinder’s physical parameters, porous medium layer, and the surrounding fluid, while the equationL2=0 does not depend on surrounding fluid parameters.[31]

The frequency equation of an impervious surface Eq.(14)whenk=0 is reduced to the product of two determinants

whereL3andL4are given in Appendix C. The equationL4=0 is independent of the nature of surface,i.e.,pervious or impervious.[20,32]

Equation (15) is satisfied, if eitherL1orL2is equal to zero. The case ofL1=0 corresponds to plane–strain vibrations of an elastic cylinder wrapped with a porous medium immersed in fluid for a pervious surface. Equation (16) is satisfied when eitherL3=0, orL4=0. The case ofL3=0 corresponds to the plane–strain vibrations for an impervious surface. From Eqs.(15)and(16),it is clear thatL2andL4are same.The case ofL2=0 corresponds to longitudinal shear vibrations which involve only longitudinal displacement. Also,sinceL2=0 holds true for a pervious surface and also for an impervious surface, we find that the longitudinal shear vibrations are independent of the nature of the surface. In Eqs.(15)and(16),at the cutoff frequency,some modes are plane–strain and others are longitudinal shear vibrations, and their phase velocities and attenuations are also different.

3. Numerical results and discussion

The numerical analysis of the frequency equations is carried out for elastic cylinder and elastic cylinder wrapped with a porous medium immersed in fluid. As obviously defined in Section 2, although various researches can be found through the motion equation of the elastic cylinder immersed in fluid,this study analyzes the acoustic behavior of an infinite length elastic cylinder wrapped with a porous medium immersed in fluid. Usually, thei-th mode belonging to the indexnis denoted as (n,i). For each ofnvalues,i.e.,n=0, 1, 2, ...,equations(13)and(14)for an elastic cylinder wrapped with a porous medium immersed in fluid,determine an infinite number of dispersion curves.

In this study, two kinds of basic independent modes of wave propagations have been considered, namely, the longitudinal mode and flexural mode (n= 0 andn= 1). We shall present the dispersion relation in terms of the frequencydependent phase velocityc(ω)=ω/Re(k)and attenuation coefficientα(ω)=8.68Im(k). The phase velocity has been normalized to the bar velocitycb=whereEais the axial Young’s modulus defined asEa=(λ+2μ)-λ2/(λ+μ).Material properties of the elastic cylinder, porous medium wrapping layer, and fluid are given in Table 2.[33,34]The surrounding and pore fluids are water. The external cylinder radiusb=0.014 m.

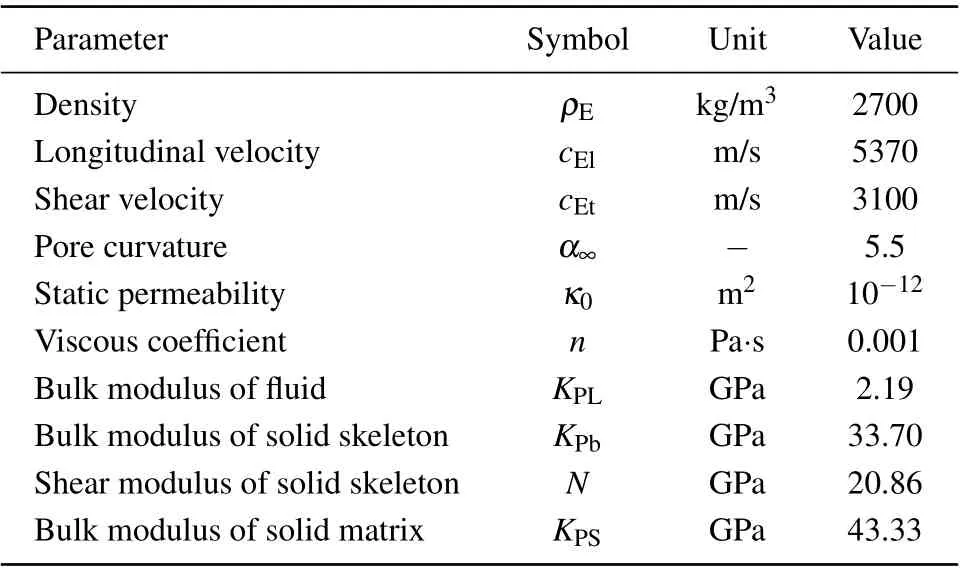
Table 2. Material properties of saturated porous medium at porosityβ =0.1.

3.1. Model verification

To check the validity of the equations derived here, the corresponding results are compared with those of an elastic cylinder immersed in fluid by setting the porosity of porous medium wrapping layer to be zero. By eliminating pore fluid effects from frequency equation of pervious surface Eq.(13),that is, settingβ →0,ρ12→0,ρ22→0,Q →0,R →0,(A-Q2/R)→λ, andN →μ, the results of purely elastic cylinder immersed in fluid are obtained as a special case. This equation coincides with the frequency equation of Venkatesan and Ponnusamy,[35,36]and it shows the exactness of our results. The frequency equation of an impervious surface Eq. (14) has no counterpart in purely elastic solid. The case ofn=0 andβ=0 is particularly simple. The displacement has only two components,which are independent ofθ. When the analysis is carried through,we obtain Eqs.(7)and(10)of Nagy and Peter.[37]Material properties are listed in Table 2.The comparison of the dispersion curves between the longitudinal modes(n=0)and flexural modes(n=1)are plotted in Fig.2,[3,38]as normalized phase velocity,c/cb,against frequency multiplied by cylinder radiusb.

Figure 2(a)shows that the dispersion curves for an elastic cylinder wrapped with a porous medium(β=0)immersed in water are not shown because almost all the parts fall on the curves for an elastic cylinder immersed in water. Only areas where they are different are shown. The bar velocitycband the normalized phase velocityc/cb, obtained from Eqs. (13)and(14), exactly match the two limiting cases, validating the equations here in the limits. The dispersion curve for an elastic cylinder immersed in water matches precisely with the data obtained by Dayal.[39]

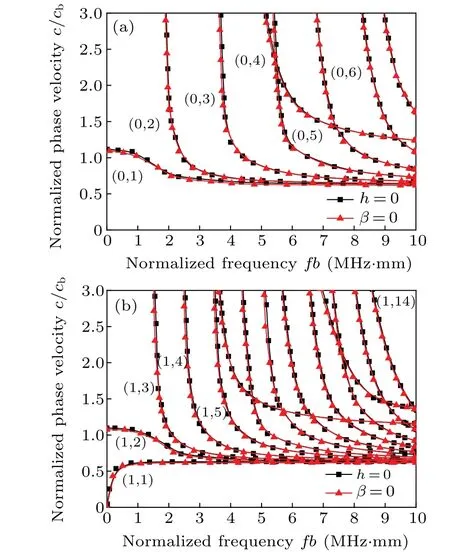
Fig.2.Comparison between dispersion curves of an elastic cylinder immersed in water and an elastic cylinder wrapped with a porous medium immersed in water:(a)longitudinal modes and(b)the first group(n=1)of flexural modes.

Figure 2(b) shows the first fourteen dispersion curves for the first group of flexural modes,i.e., corresponding ton=1. Again,the curves for the elastic cylinder wrapped with a porous medium immersed in water(β=0)are indistinguishable from those of the elastic cylinder immersed in water. All modes,(1,i),i ≥3,upward appear to asymptotically approach to the shear velocity(i.e.,cEt/cb=0.632)but the lowest mode will approach to the Rayleigh velocity. These dispersion characteristics are in good agreement with the solution of the displacement potential function in the derivation of the dispersion equation.

3.2. Dispersion curves

In this numerical example,the elastic cylinder is changed from an isotropic cylinder in Fig. 2 into a cylinder wrapped with a porous medium in Fig. 3, generating different modal waves. According to Eqs.(13)and(14),the dispersion curves of an elastic cylinder wrapped with a porous medium immersed in water for pervious surface and impervious surface are investigated numerically by considering that the porous medium layer is finite, the thickness ish=0.002 m, and the porosity isβ=0.1,the material properties of the elastic cylinder,porous medium wrapping layer,and fluid are the same as those in Fig.2.The elastic cylinder core radius isa=0.012 m.

The calculated dispersion curves of the longitudinal modes and flexural modes of an elastic cylinder wrapped with a porous medium immersed in water are presented as a function offbin Fig.3 each for a pervious and an impervious surface. The phase velocity and trend are compared with those of the elastic cylinder immersed in water model. The same trends can be observed from both results. The phase velocity of an elastic cylinder immersed in water is higher than that of an elastic cylinder wrapped with a porous medium immersed in water.Here,the presence of porous medium wrapping layer reduces the phase velocity. The phase velocity of the higherorder modes((0,i)or(1,i),i ≥3)decreases rapidly with the increase of frequency, especially at the frequencies near the cutoff.For some modes,the dispersion curves of the two cases essentially overlap each other.

Generally,the guided wave spectrum is only slightly perturbed by the porous medium wrapping layer. It is noteworthy that in this figure, the most interesting effect is the“switch over” from the 1st mode to the 2nd one aroundfb ≈2 MHz·mm for longitudinal modes (n= 0) and from the 2nd mode to the 3rd one aroundfb ≈1.5 MHz·mm for flexural modes (n=1). This anomalous behavior has been previously observed in the leaky Lamb wave spectra of both isotropic and anisotropic plates,[40,41]and can be also seen in the leaky guided wave spectra of thin shells.[42,43]For plates,the switching between the two lowest-order symmetric modes occurs if the density of the fluid approaches to the density of the solid. In our case, the density ratio is slightly lower,(ρ11+2ρ12+ρ22)/ρE≈0.94, but a cylinder wrapped with a porous medium is much more affected by fluid loading than a plate of the same material.

From Fig. 3(a), it can be observed that except for the modesL(0,1)P,all higher modes have a cutoff frequency,i.e.they do not exist below the cutoff frequency. The lowest mode(L(0,1)P) exhibits the expected behavior in that the normalized velocity approaches to unity at low frequencies. The reason for this is that the vibration asymptotically approaches to a purely axial motion, and without a standard vibration component. There is no coupling between the cylinder, porous medium wrapping layer, and viscosity-free fluid, and the effect of the surface is maximal near the cutoff frequency.As the frequency increases, the surface effect becomes pronounced on some modes but does not affect others. The phase velocity limit of the longitudinal guided wave is the same for a pervious surface and an impervious surface for an elastic cylinder wrapped with a porous medium immersed in water,while the cutoff frequency for a pervious surface is higher than that of an impervious surface. The waves for an impervious surface tend to approach to the Rayleigh wave limit more rapidly than when the surface is pervious. The trend of curves demonstrates that by enhancing the frequency to an infinite value,the phase velocity limit of the present study is approached to the Rayleigh wave’s phase velocity.

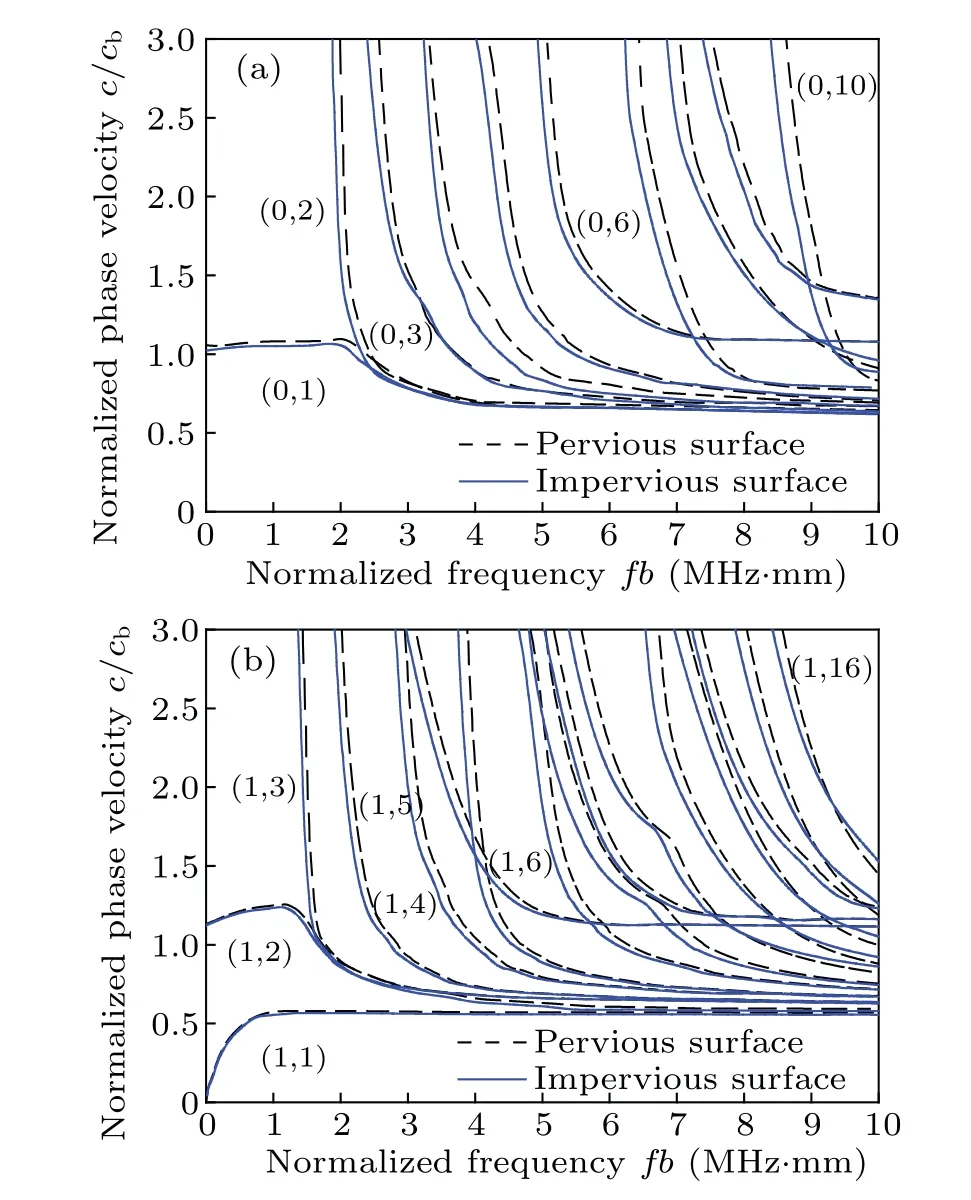
Fig.3. Calculated dispersion curves of elastic cylinder wrapped with a porous medium immersed in water (β =0.1): (a) longitudinal modes, and(b)the first group(n=1)of flexural modes.

Similar phenomenon is observed in the case of dispersion curves of pervious surface and impervious surface shown in Fig.3(b). The calculated results exhibit the asymptotic behavior both at low frequencies and at high frequencies as well as at the cutoff frequencies of individual modes. Each mode exists in a wide frequency range.There is more than one mode at any frequency, and the characteristics of each mode are unique.All higher modes fromF(1,3)Phave a cutoff frequency, and the phase velocities decrease with frequency,and slope downward,approaching to the velocitycPt/cb=0.586.

Comparing with Fig.2(b), the porous medium wrapping layer causes the flexural modes of the high-frequency domain to occur at the lower frequencies,i.e.,the phase velocity curves corresponding to the porous medium wrapping layer shifts toward the low-frequency domain in Fig.3(b). Besides,the modesF(1,1)PandF(1,2)Phave no cutoff frequencies,and the low-frequency limit of the phase velocity for the modeF(1,1)Pis zero and the high-frequency limit of phase velocity is the Rayleigh wave velocity of the porous medium wrapping layer. Such a behavior is also exhibited by waves propagating in a free bar or an isotropic plate.[44]Similarity between the two cases is not surprising since for very large radius the effect of curvature on the wave propagation in a cylinder becomes minimal. The modeF(1,1)Pis undamped as long as its phase speed is less than that of sound in the water, which corresponds toc/cb=0.303 in Fig. 3(b). All higher ((1,i),i ≥2) modes have speeds greater than 0.5cb, they suffer attenuation for all frequencies. The wavenumbers for all modes each for a pervious and an impervious surface, (1,i),i ≥2,each have a small imaginary part giving rise to leakage of energy from the cylinder to the water. For the same reason, all axisymmetric modes of Fig.3(a)are also damped. The attenuation of longitudinal modes and flexural modes in the elastic cylinder wrapped with a porous medium immersed in water is discussed further below.

Calculating Eqs. (13)–(16) determines the phase velocities and cutoff frequencies for pervious surface and impervious surface. Most of these velocities and frequencies are similar, or even the same for pervious surface and impervious surface of an elastic cylinder wrapped with a porous medium immersed in water. The relatively low-frequency part of the low-order guided wave modes is easily excited and reduces the complexity of signal processing. Therefore, it is imperative to study the propagation characteristics of loworder modes. The following research work focuses on the low-order guided wave modes in an elastic cylinder wrapped with a porous medium immersed in water for pervious surface,namely,L(0,i)P,F(1,i)P,i ≤8.

3.3. Phase velocity versus porosity of the porous medium wrapping layer

As discussed in the acoustics of the seabed as a poroelastic medium,[45]porosity is a crucial parameter that is defined as the ratio of volume of the fluid constituent to the total volume. A concrete example is presented with the static permeabilityκ0=10-12m2,and the thickness of the porous medium wrapping layerh=0.002 m to investigate the influence of the porosity on the dispersion curve. Porosityβ=0.1, 0.2, and 0.3 are considered,and the associated phase velocities are reported in Table 3.

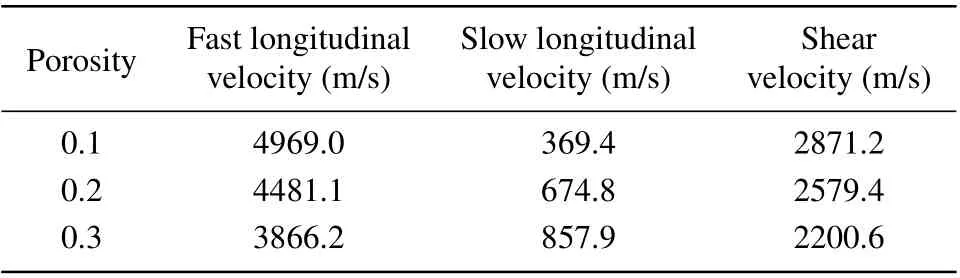
Table 3. Velocities of body sound waves in porous media with different porosities.

The effect of the porosity of the porous medium wrapping layer on the dispersion curves is presented and discussed in Fig. 4. Generally, the positive effect of the porous material is highlighted in the high-frequency domain, wherein the wavelengths are short enough. Based on the results, this issue is quickly confirmed. It is shown that the phase velocity and its limit decrease in the high-frequency domain, no remarkable changes can be seen at low frequencies by increasing the porosity. This is because the wavelength of the sound wave decreases with the increase of frequency, the influence of porosity on the dispersion characteristics begins to appear and increase,and the phase velocity limits gradually separate.

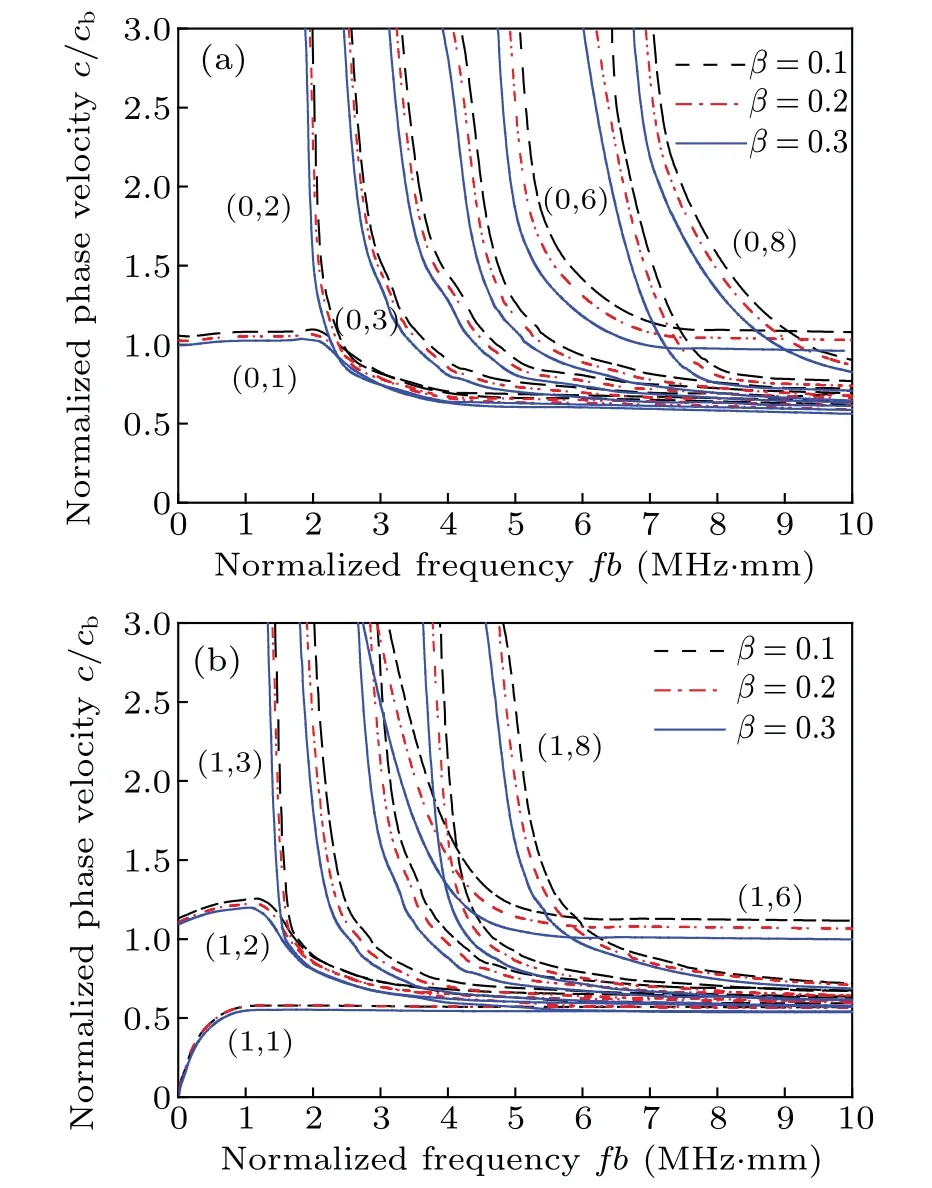
Fig.4.Calculated dispersion curves for the first eight modes in elastic cylinder wrapped with a porous medium immersed in water (h=0.002 m): (a)longitudinal modes and(b)the first group(n=1)of flexural modes.

From Fig. 4(a), the porosity has no significant effect on the trend change of the dispersion curves. When the porosity increases from 0.2 to 0.3, the trend of the normalized phase velocity is almost the same as that ofβ=0.1. An exception isL(0,6)P,an obvious decrease in the phase velocity when the porosity rises from 0.1 to 0.3, while other axisymmetric longitudinal modes’ cutoff frequencies and phase velocities decrease slightly with the porosity increasing. The velocity of the guided wavesL(0,i)P,i ≥2,approaches to that of the shear wave (2871 m/s, 2579 m/s, 2201 m/s) in the porous medium wrapping layer, which corresponds toc/cb= 0.586, 0.526,0.449 in Fig. 4(a), and the velocity ofL(0,1)Ptends toward the corresponding Rayleigh velocity. In Fig.4(b),the effect of porosity on theF(1,1)P,F(1,2)P,andF(1,3)Pmodes are not evident. The porosity significantly affects the phase velocities of the modesF(1,i)P,i ≥3, in an elastic cylinder wrapped with a porous medium immersed in fluid. As the porosity increases, the cutoff frequency decreases, and the dispersion curves of theF(1,i)P,i ≥3,slope downward,approaching to the shear wave velocity in the porous medium with different porosities.

In fact, there is a visible and direct effect between the porosity of the porous medium wrapping layer and dispersion curves in the high-frequency domain(over 400 kHz·mm).Therefore,the porosity in the medium surface layer of the elastic cylinder immersed in fluid can be analyzed by the change in the phase velocity,which provides a certain theoretical support for nondestructive testing. The porosity used in this study may lead to a new aspect of the optimization of the theory of cylinder or pipeline damage detection.

3.4. Phase velocity versus thickness of porous medium wrapping layer

Figure 5 presents the influence of the thickness of the porous medium wrapped layer on the elastic cylinder immersed in fluid. As obviously defined in boundary conditions and frequency equations, the dispersion characteristics are changed by varying the thickness of the porous medium wrapping layer,whereas the high-frequency limit to the phase velocity remains constant.

As depicted in Figs. 5(a) and 5(b), the radii of the elastic cylinder are 0.010 m, 0.012 m, and 0.013 m (Ratio of inner radius to thickness,a/h= 2.5,a/h= 6,a/h= 13), as the thickness of the porous medium wrapping layer increases,their cutoff frequencies and phase velocities decrease gradually. The dispersion characteristics of the porous medium wrapping layer on the elastic cylinder immersed in fluid are not sensitive to thickness in the high-frequency region over 8×103kHz·mm. On the contrary, there is a direct effect between the thickness of the porous medium wrapping layer and dispersion curve in the high-frequency domain over 20 kHz·mm so that by varying the porous thickness, the acoustic performance of a finite structure can be improved.The increasing of the thickness may reduce the structure’s stiffness and lead some acoustic waves to transfer through the structure in the low-frequency domain. Hence, the presence of the porous medium wrapping layer has a significant effect on the phase velocity. The effect of the porous medium wrapping layer cannot be ignored in the numerical simulation and analysis.

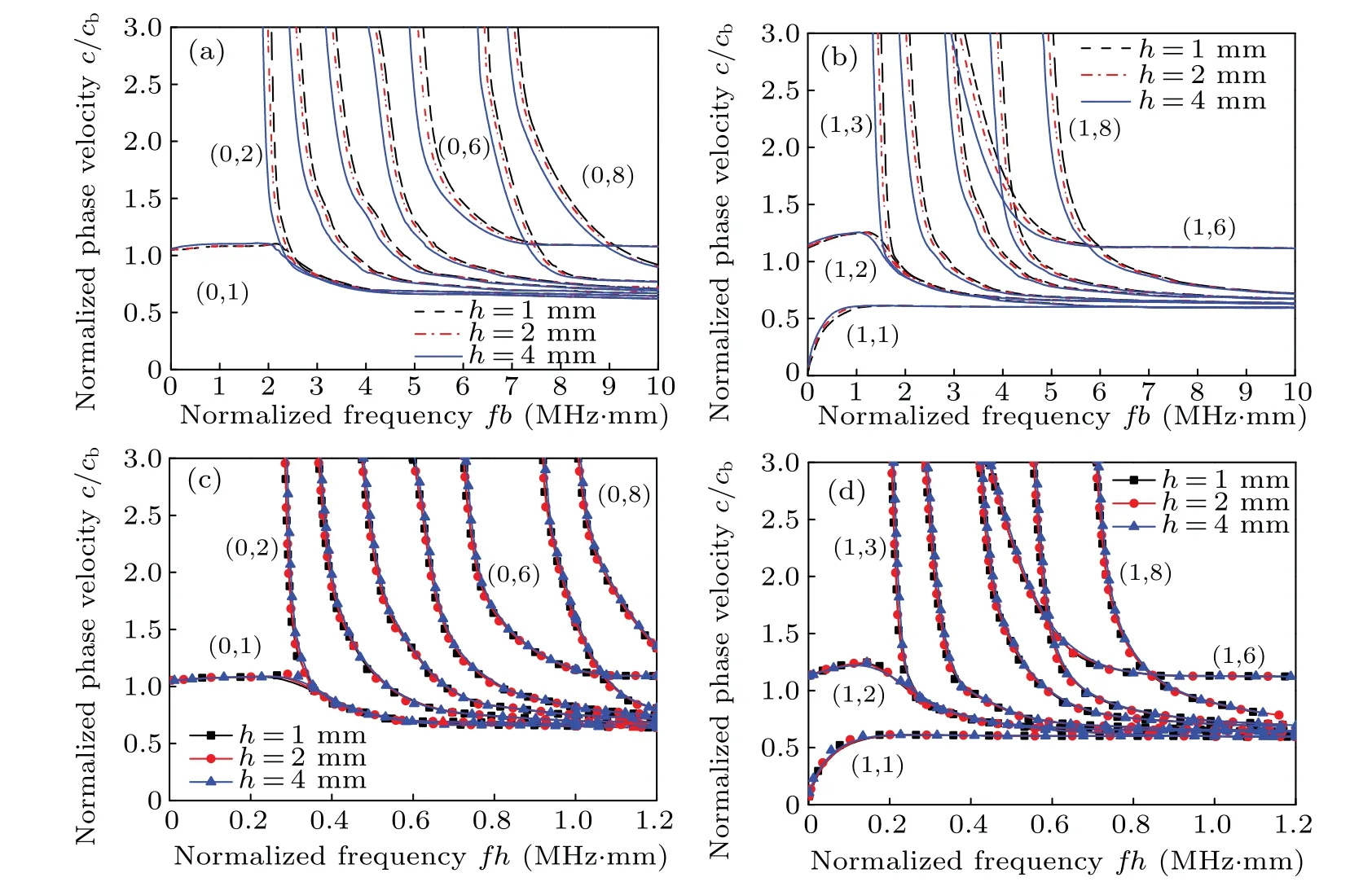
Fig.5. Calculated dispersion curves for the first eight modes in elastic cylinder wrapped with a porous medium immersed in water(β =0.1):(a)and(c)longitudinal modes,(b)and(d)the first group(n=1)of flexural modes.

Figures 5(c)and 5(d)show a new comparison between the present results(red lines,a=0.012 m,andh=0.002 m)and those of the elastic cylinder wrapped with a porous medium for different radii. To achieve this end,the radius of the elastic cylinder and thickness of the porous medium wrapping layer are 0.006 m and 0.001 m,0.012 m and 0.002 m,and 0.024 m and 0.004 m(ratio of inner radius to thickness,a/h=6). The dispersion curves of the elastic cylinder wrapped with a porous medium immersed in water are each presented as a function of the frequency-thickness productfhin Figs. 5(c) and 5(d)for a pervious surface. As illustrated,under the same ratio of inner radius to thickness (i.e.a/h=6), when the horizontal axis is expressed in terms of the frequency-thickness product,the dispersion curves of the longitudinal modes with different thickness are overlapped. The result is consistent with those of cylinder and planar substrate-elastic medium wrapping systems,[46–48]which imply that they are the special cases in this study.

3.5. Phase velocity versus static permeability of the porous medium wrapping layer

The permeability is an essential parameter of porous media,[49]which reflects the ability of porous media to transfer fluid. To determine the static permeability dependent properties of the guided waves for elastic cylinder wrapped with a porous medium immersed in water, the dispersion characteristics with static permeabilityκ0of 10-11m2,10-12m2,and 10-13m2are analyzed by setting the porosityβ=0.1.The influence of static permeabilityκ0on the phase velocities can be found from Fig.6. It shows that the phase velocity is slightly affected by the increase of static permeability.

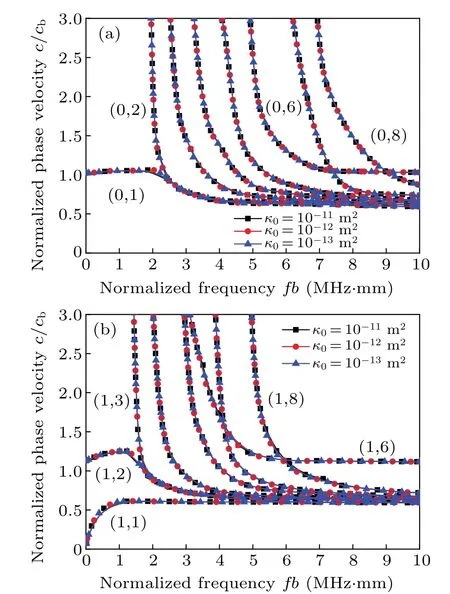
Fig.6. Calculated dispersion curves for the first eight modes in elastic cylinder wrapped with a porous medium immersed in water (β =0.1,h=0.002 m): (a)longitudinal modes and(b)the first group(n=1)of flexural modes.

3.6. Attenuation curves

Porous medium is dissipative in nature, and thus, the wavenumberkis complex. The generated waves obey a diffusion type process and therefore become attenuated. In Ref.[40],the attenuation coefficient is plotted as a function of the normalized frequencyfb. However,the attenuation coefficient is also an independent function of radius(or frequency).Therefore, we plot the normalized attenuation,i.e., the leaky attenuation over a length equal to the outer radius of the cylinder (α(ω)·b): it depends only on thefbproduct. Figure 7 shows the corresponding attenuation curve in the elastic cylinder wrapped with a porous medium immersed in water.

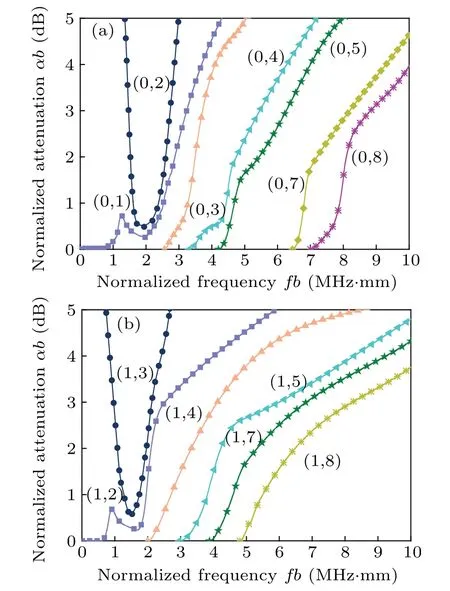
Fig.7. Attenuation curves for the first eight modes in elastic cylinder wrapped with a porous medium immersed in water(β =0.1,h=0.002 m):(a)longitudinal modes and(b)the first group(n=1)of flexural modes.

From Fig. 7(a),L(0,1)PandL(0,2)Pare the two branches produced by the above-mentioned anomalous topology (“mode switching”). The normalized attenuation ofL(0,1)Pis proportional to the cube of the normalized frequency,i.e.,αb∝(fb)3, at low frequencies, and this mode approaches to the 2nd true mode of the free rod at high frequencies and the attenuation is much higher. TheL(0,2)Pis the high-attenuation mode and decreases for higher values of frequency, the first rapidly then almost proportionally to the square of the normalized frequency,i.e.,αb∝(fb)2. On the other hand, theL(0,3)P,L(0,4)P,L(0,5)P,L(0,7)P, andL(0,8)Pmodes are undamped near their cutoff frequencies.The attenuation of the modeL(0,6)Pis so small that it cannot be shown on a scale used in Fig. 7(a). The normalized attenuations of the first six higher-order modes are shown in Fig.7(b). The attenuation of the modeF(1,6)Pis very small in this frequency range and is omitted to reduce the confusion. Figures 7(a) and 7(b) indicate that the attenuation for the flexural mode is relatively small as compared with that for the longitudinal one. Near the cutoff frequency, the reasons behind the different phenomena are explained below.

The frequency equation (15) (k= 0) can explain why there is such a big difference in the corresponding attenuation at the cutoff frequency,i.e., when their phase velocity is infinitely high and there is no energy propagation along the cylinder. Fork= 0, equation (15) is the frequency equation of plane–strain and longitudinal shear vibrations. For Eq.(15),at the cutoff frequency,those modes which are pure plane–strain vibrations produce only transverse vibrations,therefore, they are not attenuated by leakage into the fluid.TheL(0,3)P,L(0,4)P,L(0,5)P,L(0,6)P,L(0,7)P,L(0,8)P,F(1,4)P,F(1,5)P,F(1,7)P,andF(1,8)Pmodes belong to this attenuation family. The other modes which are pure longitudinal shear vibrations produce only normal vibrations therefore they are very strongly attenuated by leakage into the fluid at the cutoff frequency. TheL(0,2)PandF(1,3)Pmodes belong to this attenuation family.

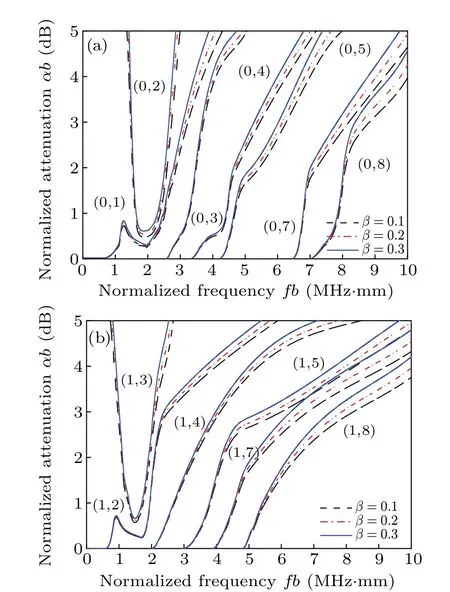
Fig.8. Attenuation curves for the first eight modes in elastic cylinder wrapped with a porous medium immersed in water (h = 0.002 m, κ0 =10-12 m2): (a) longitudinal modes and (b) the first group (n=1) of flexural modes.

Finally, the effect of the porosity of the porous medium wrapping layer on the attenuation curve is presented. Figures 8(a) and 8(b) show the attenuation curves of the elastic cylinder wrapped with a porous medium immersed in water with different porosities. As investigated by Schaap,the attenuation increases as a result of the added radiation damping.[50]In Fig. 8, the radiation damping effect increases with porosity increasing(the water in the porous medium increases with the porosity increasing). At very low frequencies (below 600 kHz·mm), this effect of the porosity is relatively small,whereas it increases distinguishably at higher frequencies than the values at low frequencies.A comparison of the attenuation between the longitudinal mode and flexural mode presented here shows that the attenuation is directly correlated with the porosity of the porous medium wrapping layer,and the attenuation increases with porosity increasing. This indicates that,in practice, a cylinder or pipeline damage can be indirectly reflected by the value of porosity. Again, there is excellent agreement between the dispersion characteristics and the attenuation behaviors.

4. Conclusions

In this work,the effect of the porous surface layer on the acoustic performance of an elastic cylinder immersed in fluid is investigated. A new model for an elastic cylinder wrapped with a porous medium immersed in fluid is presented to ascertain the effects of the porous medium wrapping layer’s porosity, thickness, and static permeability on the dispersion equation,cutoff frequency,and dispersion characteristics. The studies of longitudinal and flexural modes propagating in an elastic cylinder wrapped with a porous medium immersed in fluid for a pervious and an impervious can lead to the following conclusions.

(i) The frequency equations of longitudinal shear vibrations of an elastic cylinder wrapped with a porous medium immersed in fluid are independent of the surface of the porous medium wrapping layer with pervious surface and impervious surface,and the presence of fluid around the cylinder.

(ii)The phase velocity of an elastic cylinder is higher than that of an elastic cylinder wrapped with a porous medium immersed in water, and the phase velocity and cutoff frequency for a pervious surface are higher than those for an impervious surface. The results are compared with those for an elastic cylinder immersed in water(β=0)and validated.

(iii) There is a “mode switching” between the two loworder modes aroundfb ≈2 MHz·mm andfb ≈1.5 MHz·mm for the longitudinal modes and also for the flexural modes,respectively,when the elastic cylinder is surrounded by a porous medium wrapping layer of the same material.

(iv) The phase velocity and attenuation are directly correlated with the porosity of the porous medium wrapping layer, and increase with porosity augment. Comparing with the effect of porosity, the increase of thickness of the porous medium wrapping layer has no significant effect on the phase velocity of a pervious surface.

(v) The porous porosity is considered as the parameter that reflects the wave propagation in regions where wavelength is short enough (in this study, at the high-frequency domain over 400 kHz·mm). It is demonstrated that the value of porosity can indirectly reflect a degree of damage to cylinder or pipeline, and provide a new perspective for nondestructive testing.

Appendix A:Expression of dispersion eqnarray

The matrix elementsai jin the case of a pervious surface are as follows:

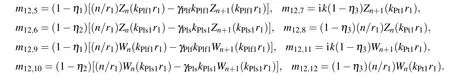
Appendix B:Expression of dispersion eqnarray

When the surface of the porous medium wrapping layer is impervious surface,the matrix elementsbijare as follows:

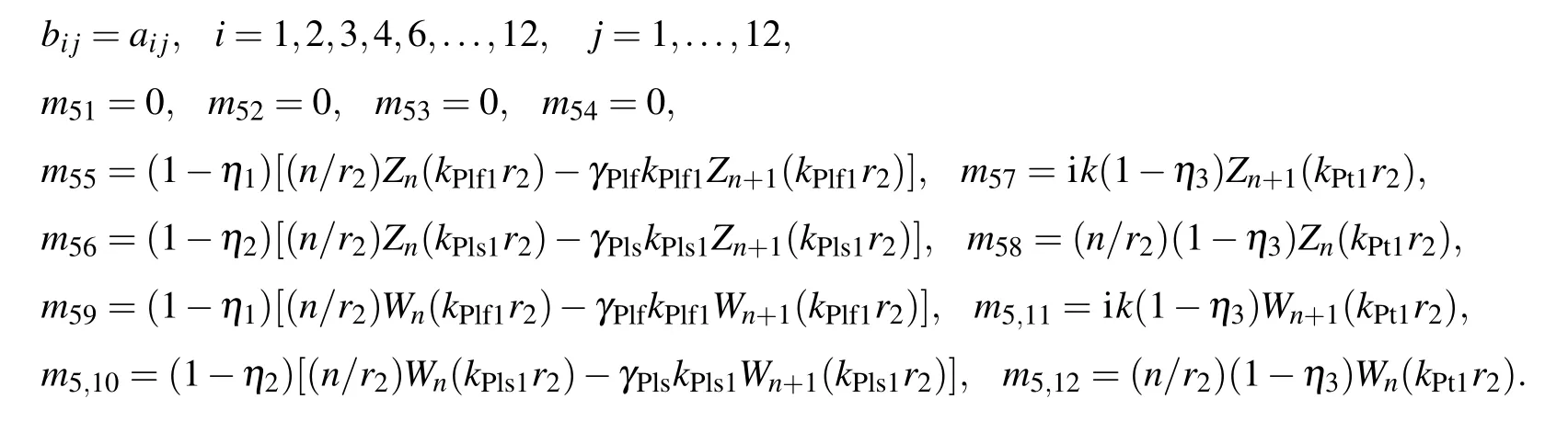
Appendix C:Expression of cutoff frequency eqnarray

The elementsai jappearing inL1andL2are defined in Appendix A and are evaluated fork=0. The matrix elements ofL1andL2are as follows:

The elementsbi jofL3andL4are defined in Appendix B and are evaluated fork=0. The matrix elements ofL3andL4are as follows:

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 12174085) and the Postgraduate Research and Practice Innovation Program of Jiangsu Province,China(Grant No. KYCX210478).