Enhancement of electron–positron pairs in combined potential wells with linear chirp frequency

Li Wang(王莉), Lie-Juan Li(李烈娟), Melike Mohamedsedik(麥麗開·麥提斯迪克),

Rong An(安榮)1,2, Jing-Jing Li(李靜靜)1,2, Bo-Song Xie(謝柏松)1,2,?, and Feng-Shou Zhang(張豐收)1,2,?

1Institute of Radiation Technology,Beijing Academy of Science and Technology,Beijing 100875,China

2Key Laboratory of Beam Technology of Ministry of Education,College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China

Keywords: electron–positron pairs,linear chirp frequency,the computational quantum field theory

1. Introduction

In recent decades, research of electron–positron pairs created from vacuum under extreme external field is an interesting topic. The existence of positron was first predicted theoretically by Dirac in 1928.[1]Soon after,it was confirmed in the laboratory by Anderson.[2]After pioneering researches of Sauter,[3]Heisenberg and Euler,[4]and Schwinger,[5]several research methods were developed, such as proper time technique,[6,7]Wentzel–Kramers–Brillouin (WKB) approximation,[8]worldline instanton technique,[9,10]quantum kinetic method,[11–14]the Furry-picture quantization,[15]the Dirac–Heisenberg–Wigner formalism,[16,17]and the computational quantum field theory.[18–20]

In the constant electric fieldE, pair creation probability is proportional to exp(-πEcr/E). The Schwinger critical field strength isEcr=1016V/cm,which is achieved at a laser intensity of roughly 1029W/cm2. Since the required field strength is far above the presently achieved laboratory electric field strength, this prediction has not been directly verified experimentally. With the rapid development of laser technique,it is believed that the laser intensity will be close to the Schwinger critical field strength. In the famous experiment at Stanford Linac Acceleration Center (SLAC),[21]pair creation can occur in laser-electron-beam collisions. The high-energy photons produced by Compton scattering collide with laser photons to produce electron–positron pairs through Breit–Wheeler process. Although the existingγ-ray sources do not meet the experimental requirements,the theoretical study of Breit–Wheeler process is a promising direction.[22]

So far, three mechanisms have been proposed for the creation of electron–positron pairs. Electron–positron pairs are created by the Schwinger mechanism, which requires a strong field.[23–25]In multiphoton processes, the creation of electron–positron pairs under the alternating field requires a high oscillation frequency.[26–29]By combining a strong and constant field with a weaker and high frequency oscillating field, electron–positrons pairs can be created through the dynamically assisted Sauter–Schwinger effect, where the paircreation probability is strongly enhanced.[30–38]

In order to lower the threshold of pair creation, many facilities have been proposed, such as multiple well-barrier structures,[39]the symmetric potential well,[28]oscillating Sauter potential,[40]and asymmetric Sauter potential well.[41]The number of created electrons in the symmetric potential is more than that in the asymmetric potential due to the two edges of the potential well.[28]For a static Sauter potential well,though the bound state promotes the generation of electron–positron pairs, the inhibitory effect of Pauli blocking cannot be ignored.[40,42]On the contrary, Pauli blocking has a weak effect on the creation of electron–positron pairs in an oscillating potential well.[27]Furthermore,multiphoton processes are highly depends on the oscillating frequency. By combining a static potential well with an alternating one, the bound state provides a bridge for the multiphoton process,and reduces the required frequency.[28]According to energy spectrum analysis, the energy of created electron is affected by the energy level of bound state and laser frequency. In the laboratory laser field, frequency modulation has more real significance because of chirp pulse amplification technique.[43]Therefore,the effect of frequency modulation on the creation of electron–positron pairs attracts much attention.[44–46]Considering chirp effect, the number of electrons created under time-dependent electric field can be increased significantly for certain modulation parameters.[47–49]Enhanced electron–positron pairs production by frequency modulation in one- and two-color laser pulse fields is also studied.[46]The effect of linear chirp on pair creation process in space-dependent electric field is worth studying. To our best knowledge,the effect of linear chirp frequency on pair creation under combined potential wells has not been studied. The enhancement of electron number under different frequency modulation parameters remains to be studied.

In this paper, the effect of linear chirp frequency on pair creation in combined potential wells is investigated by using the computational quantum field theory. First, the number of created electrons varying with chirp parameter is obtained.Then, the creation mechanism of electron–positron pairs is studied by analyzing the energy spectrum of created electrons.Furthermore,we show contour plot of the final number against chirp parameters under combined potential wells and a single potential well. The effect of frequency modulation on a single potential well is stronger than that of combined potential wells.

This paper is organized as follows. In Section 2, we describe the outline of computational quantum field theory and illustrate combined potential wells. In Section 3, the final number and energy spectrum of created electrons under different frequency-modulation parameters are simulated. The calculation results are compared with those of a single potential well. In Section 4,we summarize our work.

2. The framework of computational quantum field theory and the external field

The computational quantum field theory is a theory that combines quantum mechanics with classical field theory. It provides an effective framework for describing multi-particle systems,especially those involving particle generation and annihilation processes. The time evolution of electron–positron field operator ?ψ(z,t)can be obtained by the Dirac equation[18]

whereαzandβare thezcomponent and diagonal parts of the spin Dirac matrices,respectively,cis the speed of light in vacuum,andV(z,t)is external field that varies with timetin thezdirection. The atomic units (ˉh=e=me=1) are used for convenience. By introducing the creation and annihilation operators,the field operator ?ψ(z,t)can be decomposed as follows:

where ∑p(n)represents summation over all positive(negative)energy,pandndenote the momenta of positive-and negativeenergy states,Wp(z)=〈z|p〉andWn(z)=〈z|n〉are positive and negative energy eigenfunctions of the field-free Dirac equation,Wp(z,t)=〈z|p(t)〉andWn(z,t)=〈z|n(t)〉are the time evolution ofWp(z)andWn(z),respectively.

From Eq.(2),we obtain

whereUpp′(t)=〈p|?U(t)|p′〉,Upn′(t)=〈p|?U(t)|n′〉,Unn′(t)=〈n|?U(t)|n′〉,andUnp′(t)=〈n|?U(t)|p′〉,the time-ordered propagator ?U(t)=exp{-itdτ[cαz?p+βc2+V(z,τ)]}.

In Eq. (2), the electronic portion of the field operator is defined as ?ψe(z,t)≡∑p?bp(t)Wp(z). Thus, we can obtain the probability density of created electrons by

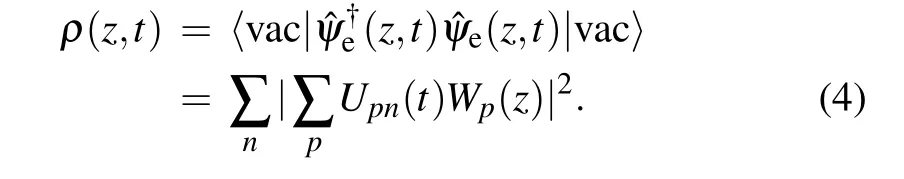
By integrating this expression over all space, the number of created electrons can be obtained as

The time-ordered propagatorUpn(t) can be numerically calculated by employing the split-operator technique. Therefore,according to Eqs.(4)and(5)we can compute various properties of the electrons produced under the action of the external potential.

In this paper,our configuration of potential is Here,S(z) ={tanh[(z-D/2)/W]-tanh[(z+D/2)/W]}/2,Dis the width of the potential well, andWis the width of the potential well edge,which corresponds to the intensity of the electric field.V1andV2are the depth of the static and the oscillating potential well, respectively. In the cases oft0＜t ＜t0+t1, combined potential wells consist of a static potential well with a depth ofV1and an oscillating potential well with an amplitude ofV2. The oscillation frequency is linearly time dependent,whereω0is the fundamental frequency,bis the chirp parameter, describing the change in frequency over time. In the cases of 0＜t ＜t0andt0+t1＜t ＜t1+2t0,it describes turn-on and turn-off processes of combined potential wells, respectively. For simplicity, the phaseφis set to 0 throughout the paper.

In Fig.1,the contour profile plot of the space-time structure of combined potential wells is presented, in which panels (a) and (b) are for the oscillating and the static potential well,respectively. The edge and width of combined potential wells are all set toW=0.3λe,D=10λe, whereλe=1/cis the Compton wavelength of the electron. The potential well depths are set toV1=V2=1.5c2. The frequency parameters are set toω0=0.5c2,b=0.0067c4,witht1=20π/c2a.u. being the interaction time. In order to facilitate data analysis,c4is taken as the unit of chirp parameterb. The opening and closing times are all set tot0=5/c2a.u. The space size is set toL=2,which ensures that all electrons generated during the numerical simulation are counted.

Fig.1.Contour profile plot of the space-time structure for combined potential wells,i.e.,(a)for the oscillating potential well,(b)for the static potential well. The fundamental frequency is set to ω0 =0.5c2. The chirp parameter is set to b=0.0067c4, where t1 =20π/c2 a.u. The space size is set to L=2. Other parameters are set to V1=V2=1.5c2,W =0.3λe,D=10λe,λe=1/c,and t0=5/c2 a.u.

First, in Fig. 1(a), the depth of the oscillating potential well slowly reaches its maximum att=0,and then the oscillation speed becomes faster and faster as time goes on. During the closing process of oscillating potential well,the depth gradually approaches to 0. Note that the depth is continuously and slowly varying from the value att=t1,rather than suddenly returning to the maximum. This reduces the error caused by the instantaneous opening and closing of the potential well.In Fig.1(b),the static potential well opens and closes slowly. The depth and the width remain unchanged duringt0＜t ＜t0+t1,which provides stable bound states for multiphoton processes.

3. Numerical results

In this section, numerical results are mainly illustrated,where relevant parameters are set toD=10λe,W=0.3λe,t0=5/c2a.u.,L=2,andt1=20π/c2a.u.

Fig.2. Number of created electrons as a function of chirp parameter b for ω0=1.0c2. Other parameters are the same as in Fig.1.

The final numberNof created electrons varying with chirp parameterbis presented in Fig. 2. The fundamental frequency is set toω0=1.0c2. Whenb=0, the frequency is fixed atω0=1.0c2. In strictly physical terms, the termbtatt=t1should be less than the fundamental frequencyω0,i.e.,b ＜ω0/t1. The region of chirp parameterb,which is not physically strict, is also studied, and the two regions are distinguished by the dotted line in Fig. 2. On the one hand, we study the results in a physical context,and on the other hand,we can incidentally observe phenomena beyond physics. With the increase of chirp parameterb, the final number first increases quickly,then decreases slowly. Whenb=0.019c4,the final number of created electrons reaches the maximum. Obviously, the frequency modulation has an enhancement effect on the number of electrons. However,whenb ＞0.019c4,the number decreases. For larger chirp parameterb,the frequency spectrum extends to the super high frequency region, which increases high-frequency suppression. According to Ref.[26],for larger frequencies, electrons and positrons do not have enough time to separate and eventually annihilate within half an oscillation period,resulting in this high-frequency suppression phenomenon. In addition,there are many peaks with the period of 0.0016c4. This phenomenon is caused by the time crystals made of electron–positron pairs, which describes the appearance and disappearance of electron–positron pairs.[50]The period of oscillation can be traced back to Eq.(6). When the total depth of combined potential wells att=t0+t1reaches the maximum,i.e.,ω0t1+=2nπ,n=1,2,3...,the generation rate of electrons increases to the maximum. Therefore,an additional peak occurs when the chirp parameterbincreases by 2π/?0.0016c4,or the fundamental frequencyω0increases by 2π/t1?0.1c2,which is verified in Fig.2. Since the peak period depends on the numerical simulation timet1,the numerical simulation time cannot be infinite.Although the resulting error is inevitable,it can be reduced by increasingt1in calculation.

The electron number varying with time and energy spectrum of electrons are presented in Figs.3(a)and 3(b),respectively. The fundamental frequencyω0is the same as in Fig.2.In Fig. 3(a), whenb=0, the number of electrons increases with a fixed period over time. Whenb=0.0080c4, 0.019c4,and 0.030c4,the number of electrons changes faster and faster over time because the frequency increases linearly. As the chirp parameter increases fromb= 0 to 0.019c4, the final number also increases. Whenb=0.030c4,although the number of electrons increases with time,the growth rate decreases,so that the final number is less than that ofb=0.019c4. The reason for this result is the phenomenon of high frequency suppression caused by frequency modulation, which will be explained later.

Fig.3. (a) The number of created electrons as a function of time and(b) energy spectrum of created electrons for b=0 (the black dashed curve), 0.008c4 (the red dotted curve), 0.019c4 (the blue solid curve),and 0.030c4 (the green dotted and dashed curve). The fundamental frequency is set to ω0=1.0c2. Other parameters are the same as in Fig.1.

In Fig.3(b),whenb=0,energy spectrum has several distinct peaks and narrow energy region. With the increase ofb,energy spectrum widens and the number of peaks increases.This reflects that frequency modulation affects multiphoton processes. The energy of photon absorbed through multiphoton processes under a fixed frequency is single. Therefore,the number of peaks in energy spectrum is small,and the distribution of peaks is relatively discrete. Whenb=0.008c4,0.019c4, and 0.030c4, frequency modulation widens the frequency spectrum, thus providing a wealth of photons of different energies for multiphoton processes. The effects of frequency modulation on energy spectrum and frequency spectrum will be illustrated in the following.

The probability density of created electrons for different chirp frequencies is presented in Fig.4. The fundamental frequencyω0is the same as in Fig. 2. Other parameters are the same as in Fig. 1. The probability density presents obvious symmetry. Whenb=0,the curve has a primary peak atz=0 and two secondary peaks inside the potential well. The probability density is periodically distributed outside the potential well. With the increase ofb,the number of primary peaks inside the potential well increases. The probability density is non-uniformly distributed outside the potential well. Compared with fixed frequency, frequency modulation enhances the interference effect of electrons. This is because electrons produced under frequency modulation have a broader energy spectrum and higher energy. The high energy electrons produced from one oscillating period can keep up with the electrons produced from the previous oscillating period,so the interference effect of electrons is enhanced.

Fig.4. The probability density of created electrons for b=0(the black solid curve),0.0056c4 (the red dotted and dashed curve),0.0087c4 (the blue dotted curve). The fundamental frequency is set to ω0 =1.0c2.Other parameters are the same as in Fig.1.

In Fig. 5, energy spectrum of created electrons under a fixed frequency and frequency modulation is presented. The black dotted curve corresponds to the fixed frequency withω0=1.9c2,b=0. The solid red curve indicates frequency modulation withω0=1.9c2,b=0.0016c4. In Fig. 5(a), we present the entire energy spectrum of one-, two-, and threephoton processes. The peak value of energy spectrum attenuates exponentially with multiphoton processes. Compared with the fixed frequency, the peak under frequency modulation shifts to the higher energy region. In Figs.5(b)–5(d),we analyze the peaks in detail.According to Ref.[28],we can obtain the energy levels of bound statesE1=-0.4247c2,E2=-0.3069c2,E3=-0.1361c2,E4=0.0680c2,E5=0.2919c2,E6=0.5260c2,E7=0.7618c2, andE8=0.9778c2. The energy of an electron produced under the fixed frequencyω0is derived fromE=Ei+nω0, wherei=1,...,8,nstands for multiphoton processes. In Fig. 5(b), energy peaks of electrons created in the one-photon process are analyzed. It is found that energy peaksE=1.56c2, 1.74c2, 1.95c2, 2.19c2,2.44c2,2.69c2,2.91c2for fixed frequency are consistent withE=Ei+1.9c2within the limits of error, wherei=2,...,8.The energy of photon absorbed in the one-photon process isω0=1.9c2. Similarly, energy peaks on the red solid curveE′= 2.01c2, 2.27c2, 2.54c2, 2.8c2are derived fromE′=Ei+(ω0+bt1)fori=4,...,7. The energy of absorbed photon isω0+bt1=2.0c2. In addition, the peakE′=1.47c2is derived fromE′=E1+1.9c2. Obviously,photons of modulation frequency are diverse. It can be inferred that energy peaks of electrons created under linear chirp frequency are derived fromE′=Ei+n(ω0+bt1). In Figs.5(c)and 5(d),this inference is well verified. Frequency modulation enhances multiphoton processes by increasing the energy of photon. Hence,with the increase of photon energy, the energy spectrum of created electrons becomes wider and higher.

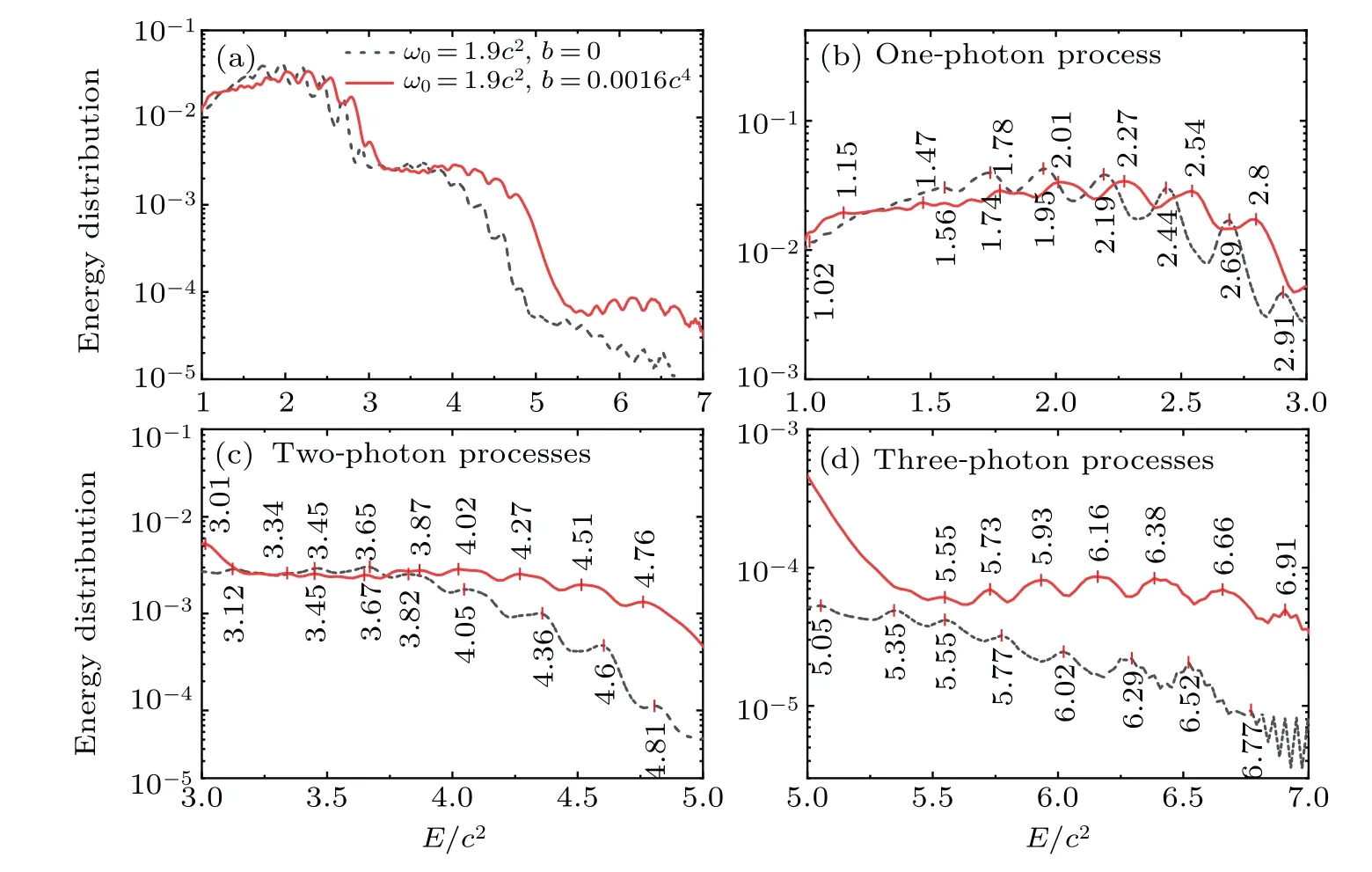
Fig.5. Energy spectrum of created electrons under the fixed frequency (the black dotted curve) with ω0 = 1.9c2, b = 0 and frequency modulation(the red solid curve)with ω0=1.9c2,b=0.0016c4. Other parameters are the same as in Fig.1.

Fig.6. Number of created electrons as a function of chirp parameter b for ω0 =0.5c2 (the black dotted curve), 1.5c2 (the red dotted and dashed curve),1.9c2(the blue dashed curve),and 2.0c2(the green solid curve). Other parameters are the same as in Fig.1.

In Fig. 6, the final number of created electrons varying with chirp parameterbfor different fundamental frequencies is presented. Whenω0=0.5c2, frequency modulation promotes the creation of electron–positron pairs. The final number of electrons increases from 1.87 to 4.76.The optimal chirp parameter isb=0.025c4. Whenω0=1.5c2,the final number of created electrons increases from 4.19 to 5.39. The optimal chirp parameter decreases tob=0.013c4. Whenω0=1.9c2,the optimal chirp parameter isb=0.0016c4. It is found that,with the increase of fundamental frequency,the optimal chirp parameter decreases gradually. Furthermore, the chirp effect is sensitive to low frequencies. Whenω0=2.0c2, with the increase of chirp parameterb, the final number decreases directly. Frequency modulation blocks the creation of electron–positron pairs under high fundamental frequencies.

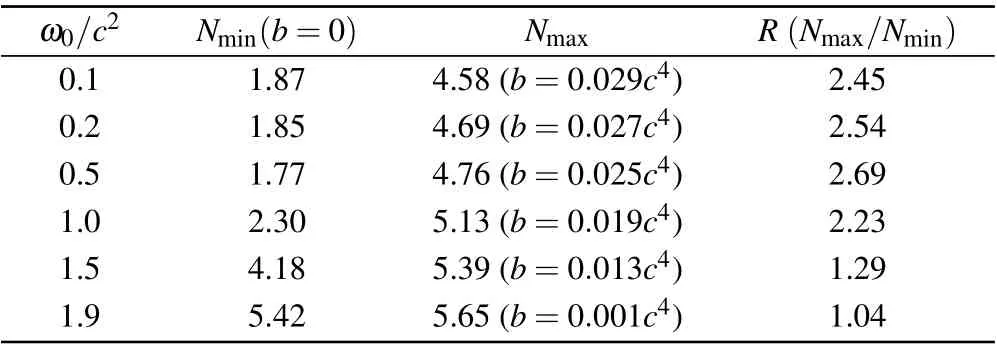
Table 1. The maximum,the minimum number of created electrons and the ratio between them for different fundamental frequencies.

Table 1 presents the maximum, the minimum number of created electrons and the ratio between them forω0＜2.0c2.The minimum number of electrons is created at a fixed frequency.The optimal chirp parameterbdecreases with increase of fundamental frequencyω0, exhibiting negative nonlinear relationship. With the increase of fundamental frequencyω0,the minimum number of electrons increases quickly.The maximum number of electrons under different fundamental frequencies varies very little. Hence, the number of electrons created at high frequencies can also be obtained at low frequencies through frequency modulation. From the ratio between the maximum and the minimum,frequency modulation is sensitive to low fundamental frequencies. With appropriate chirp parameters,the number of electrons can be increased by 2–3 times.

In Fig. 7, the number of created electrons varying with fundamental frequencyω0is presented. Here, chirp parameter is set tob=0. With the increase ofω0, the number of electrons varies nonlinearly,which is related to the change of mechanism of electron–positron pairs. In a single subcritical static potential well, the Schwinger mechanism is dominant,and the pair production rate is very small, see Fig. 3(e) in Ref. [28]. For an subcritical oscillating potential well, multiphoton processes are stronger for the higher frequencies,see Figs.1(a)and 1(b)in Ref.[26]. In combined potential wells,the number of created electrons in Fig. 7 is the result of several competitive mechanisms,including the Schwinger mechanism, multiphoton processes, and the dynamically assisted Sauter–Schwinger effect. In the low frequency region, although the Schwinger mechanism is strong, the dynamically assisted Sauter–Schwinger effect and multiphoton processes are both weak. The number of created electrons is relatively small. With the increase ofω0, the Schwinger mechanism is weakened,but multiphoton processes are strengthened. These discrete bound states of the static potential well also facilitate multiphoton processes.[28]Meanwhile, the dynamically assisted Sauter–Schwinger effect is enhanced by the combination of a high frequency oscillating potential well and a static potential well. Therefore,there is a significant increase in the number of electrons forω0＜2.0c2. Whenω0＞2.0c2, the number of created electrons no longer increases with the increase ofω0,which is the phenomenon of high frequency suppression. The oscillation of electron number with frequency is affected by coherence effects in the single-photon regime,see Fig.3 in Ref.[27].

Fig.7. Number of created electrons varying with fundamental frequency ω0 for b=0. Other parameters are the same as in Fig.1.

Figure 8 presents the frequency spectrum under frequency modulation. The depth of potential well varies aperiodically with time under linear frequency modulation. Due to the limited simulation time, the spectrum cannot display the fundamental frequency. In Fig. 8(a), when modulation parameters are set toω0=1.5c2andb=0.005c4,the frequency spectrum is symmetric aboutω0+bt1=1.8c2. For high fundamental frequencies,the frequency spectrum can be extended to the ultrahigh frequency region by increasing chirp parameterb.Due to high frequency suppression effect,the creation of electron–positron pairs does not benefit from frequency modulation.As shown in Fig. 7, when the frequency is increased from the high frequency region to the ultrahigh frequency region,the electron number is already very large. There is not much room for growth. Hence,the enhancement effect of frequency modulation on the number of electrons is not sensitive to high fundamental frequencies. In Fig. 8(b), the spectrum extends from the low frequency region to the high frequency region.For low fundamental frequencies, the weak high-frequency field appears under frequency modulation, which combines with the strong static field to enhance the dynamically assisted Sauter–Schwinger effect. Meanwhile, multiphoton processes are also enhanced by high frequencies field. Therefore, frequency modulation is sensitive to low frequencies.

Fig.8. The frequency spectrum under frequency modulation for (a)ω0=1.5c2,b=0.005c4,and(b)ω0=0.2c2,b=0.014c4.

Next,we study the enhancement effect of frequency modulation in a single oscillating potential well. Figure 9 shows the number of electrons created under a single oscillating potential well varying with chirp parameterb. The depth of the potential well is set toV2=1.5c2. For different fundamental frequencies, the maximum number of electrons generated after frequency modulation is in the same order of magnitude.Whenω0=0.1c2, the number of created electrons generated at the fixed frequency is extremely low because the Schwinger mechanism is dominant. As described above, the high frequency component of the spectrum caused by chirped parameterbenhances multiphoton processes and greatly promotes the generation of electron–positron pairs. There is huge room for growth in the number of electrons. With appropriate chirp parameterb, the number can be increased by several orders of magnitude. Furthermore,as the fundamental frequency increases, multiphoton processes intensify and the number of electrons produced at a fixed frequency increases. Thus,with the increase ofω0, the frequency modulation effect becomes less sensitive,which is consistent with the conclusion of combined potential wells.

Fig.9. Number of created electrons as a function of chirp parameter b for ω0 =0.1c2 (the black dotted curve), 0.5c2 (the red dotted and dashed curve),1.5c2(the blue dashed curve),and 2.0c2(the green solid curve). The potential well depths are set to V1 =0,V2 =1.5c2. Other parameters are the same as in Fig.1.

In Fig.10,we present the contour plot of the final number varying with fundamental frequencyω0and chirp parameterb. Frequency modulation parametersω0andbare all divided into 20 grids. Discrete parametersω0andbare integer multiples of 0.1c2and 0.0016c4, respectively. For an arbitrary set of fundamental frequency and chirp parameter,we can adjust these two parameters according to Fig.10 to get the same number of electrons. From Fig. 10(a), the number of electrons created under a single oscillating potential well can be enhanced by three orders of magnitude. These dotted contour lines are basically parallel and linearly decrease. For low fundamental frequencies, the pair generation was dominated by the Schwinger mechanism. Under the condition of subcritical field strength, the pair generation rate is very small. The final number remains the same when the sum ofω0andkbt1equals the same constant. Here,k ?1.3 is the empirical coefficient derived from dotted contour lines. With the increase ofω0+kbt1,the final number increases rapidly. This is because multiphoton processes play a dominant role.

Fig.10. The contour plot of the final number varying with fundamental frequency ω0 and chirp parameter b for (a) a single oscillating potential well with V1 =0, V2 =1.5c2, (b) combined potential wells with V1=V2=1.5c2. Other parameters are the same as in Fig.1.

In Fig.10(b),the number of electrons created under combined potential wells can only be enhanced by two or three times.These contour lines are nonlinear at the high fundamental frequency in the high chirp parameter region. When the fundamental frequency and the chirp parameter exceed certain values, the number of electrons decreases. In addition,contour lines of the low frequency region also have obvious nonlinearity. In the low fixed frequency region, the number of electrons generated in combined potential wells is several orders of magnitude higher than that in the single oscillating potential well. After frequency modulation, the final number of electron–positron pairs in combined potential wells and the single potential well is in the same order of magnitude.Comparatively,frequency modulation has relatively higher enhancement effect on electron–positron pair creation in a single oscillating potential well.

4. Conclusions

In summary,we have investigated the enhancement effect of frequency modulation on the electron–positron pair creation from vacuum under combined potential wells using the computational quantum field theory. The energy spectrum and the probability density under different modulation parameters are analyzed. The influence of linear frequency chirp on the final number of electrons created by combined potential wells and a single potential well is discussed. The main results are given as follows:

(i) In combined potential wells, frequency modulation promotes the creation of electron–positron pairs. Under frequency modulation, the number of electrons increases in growth rate and the energy spectrum becomes higher and wider. Compared with the fixed frequency, the spatial probability density of electrons shows a stronger interference effect. The chirp parameter adjusts the generation mechanism.In the low frequency region,multiphoton processes and the dynamically assisted Sauter–Schwinger effect can be enhanced by selecting appropriate chirp parameters,thus promoting the number of created electrons by 2 to 3 times.

(ii) In the single oscillation potential well, frequency modulation has a strong enhancement effect on the generation process of electron–positron pairs and is very sensitive to the low frequency region. When appropriate chirp parameters are selected,the number of created electrons can be increased by several orders of magnitude.

(iii)The optimal chirp parameter decreases linearly with the increase of fundamental frequency.

The number of electrons created mainly by the Schwinger mechanism in a low fixed frequency is small.With appropriate chirp parameters, the frequency spectrum of linear frequency modulation covers both low and high frequency regions, enhancing multiphoton processes and the dynamically assisted Sauter–Schwinger effect. The number of created electrons is enhanced. When the frequency spectrum expands into the ultrahigh frequency region, high frequency suppression is activated, preventing electron production. In a single oscillating potential well, there is a dramatic increase in the number of electrons after frequency modulation. In the low frequency region,frequency modulation is more sensitive to a single potential well than combined potential wells. The main reason for this difference is the extremely low number of created electrons under a single potential well.

In order to investigate the effect of frequency modulation on the number of created electrons,we have studied combined potential wells and find that the number of electrons increases by two to three times.Considering the chirp effect,the number of electron could be increased more dramatically in a single potential well.For other external fields,the effect of frequency modulation on the yield of electrons may be stronger,which is beyond the scope of the present paper.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11635003, 11025524,11161130520,11875007,and 12047513)and the Reform and Development Project of Beijing Academy of Science and Technology(Grant Nos.13001-2110 and 13001-2114).