一類帶有對數(shù)非線性項(xiàng)的擬線性橢圓方程解的存在性及多重性
劉曉莉,賈 高
(上海理工大學(xué) 理學(xué)院,上海 200093)
§1 引言
考慮如下擬線性橢圓方程弱解的存在性和多重性
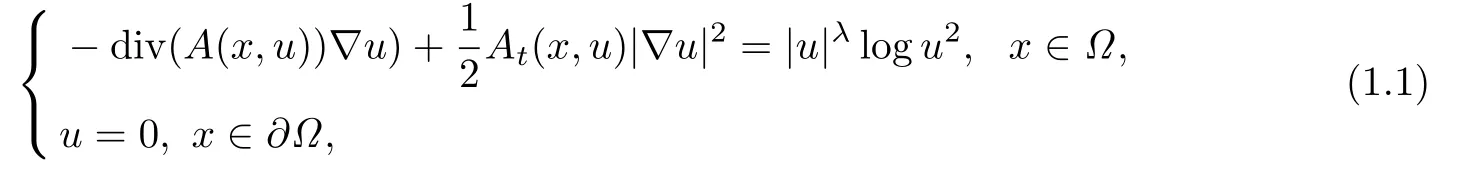
其中Ω ?RN是一個(gè)具有光滑邊界的有界區(qū)域,N ≥2,λ ∈(1,2*-1),A(x,t),At(x,t)是RN ×R上的Carath′eordory函數(shù).方程(1.1)和Schr?dinger方程的駐波解是密切相關(guān)的,并且廣泛應(yīng)用在等離子體物理學(xué),量子光學(xué),量子力學(xué)和超流體理論等領(lǐng)域的研究中(見[1-2]).
問題(1.1)對應(yīng)的自然泛函為
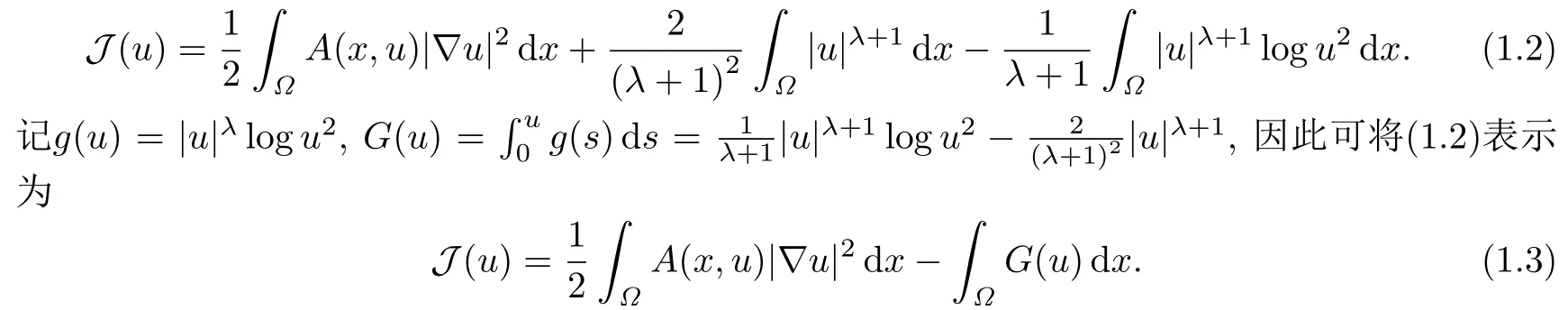
容易看出,|g(u)| ≤C1(1+|u|θ),θ ∈(λ,2* -1),C1>0,所以對(Ω),關(guān)于u是C1的(見[3]).然而,由于泛函的主體部分中有函數(shù)A(x,t),導(dǎo)致泛函在(Ω)上有可能不是良定義的.進(jìn)一步發(fā)現(xiàn),即使A(x,t)是光滑有界的正函數(shù),這時(shí)泛函J在(Ω)是良定義的,但是如果,J只能在方向上是Gateaux可導(dǎo)的.
近年來,一些學(xué)者通過使用非光滑臨界點(diǎn)理論[4-12]研究如下類型問題

例如,在[6]和[10]中,Candela,Palmieri和Salvatore在有界區(qū)域考慮問題(1.4),非線性項(xiàng)g(x,t)關(guān)于t滿足合適的增長條件,利用弱形式的山路引理和對稱山路定理,證明解的存在性和多重性.進(jìn)一步,Candela 和Salvatore在[8]中證明了當(dāng)Ω是無界區(qū)域時(shí),問題(1.4)徑向解的存在性.而帶有對數(shù)非線性項(xiàng)的Schr?dinger方程也引起了很多學(xué)者的興趣,并得到了系列重要成果,見[13-19].
受到上述及相關(guān)成果的啟發(fā),對函數(shù)A(x,t)提出合適的條件,使泛函在空間上是C1的.因?yàn)榉汉赡懿粷M足經(jīng)典的(CPS)條件[9],將使用弱形式的(CPS)c條件,以及與之對應(yīng)的山路引理和對稱山路定理.盡管本文的非線性項(xiàng)是對數(shù)形式,但是它并不能滿足之前很多文獻(xiàn)對于非線性項(xiàng)的要求,比如AR條件,這也是本文的創(chuàng)新點(diǎn)和需要克服的難點(diǎn).
在本文中,假設(shè)函數(shù)A(x,t)滿足以下條件.(A0)A(x,t)是C1的Carath′eordory函數(shù),即
A(·,t):(x,t)∈R對于所有t ∈R是可測的,
A(x,·):t ∈R(x,t)∈R對幾乎處處的x ∈Ω是C1的;(A1) 當(dāng)t有界時(shí),A(x,t)和At(x,t)是本性有界的,即

(A5)A(x,t)=A(x,|t|) a.e.x ∈Ω,對所有t ∈R.
注記1.1經(jīng)過簡單計(jì)算可得,若a(x)是可測函數(shù),且滿足0<a1≤a(x)≤a2,那么A(x,t)=a(x)(1+|t|λ-1)滿足條件(A0)-(A5).
注記1.2根據(jù)條件(A1)-(A4),可得當(dāng)|t|≥R0時(shí),有
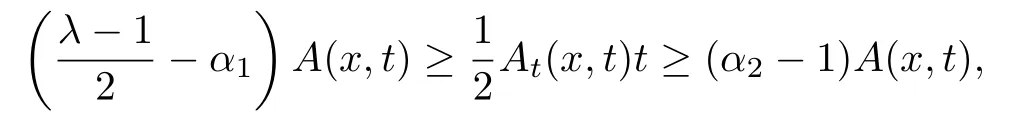
經(jīng)過簡單的計(jì)算,可知存在正常數(shù)C2,C3,當(dāng)|t|≥R0時(shí),成立
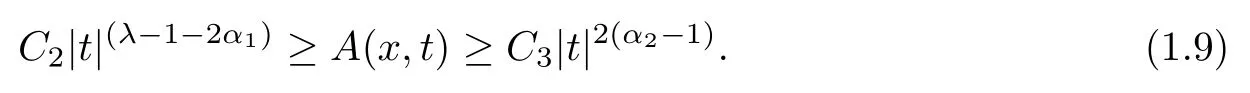
注記1.3因?yàn)?/p>

故存在正常數(shù)C4,C5,成立

注記1.4由于

故對于任意的∈>0,存在常數(shù)C∈,成立

本文的主要結(jié)果如下.
定理1.1設(shè)N ≥2,λ ∈(1,2*-1),函數(shù)A(x,t)滿足條件(A0)-(A4),則問題(1.1)存在一個(gè)山路解.
定理1.2設(shè)N ≥2,λ ∈(1,2*-1),函數(shù)A(x,t)滿足條件(A0)-(A5),則問題(1.1)存在無窮多個(gè)非平凡解.
§2 預(yù)備知識(shí)和主要引理
首先說明文中的一些符號.Lp(Ω)(1≤p <+∞)和(Ω)是標(biāo)準(zhǔn)的Lp空間和Hilbert空間,它們的范數(shù)分別定義為是Lebesgue可測且本性有界的函數(shù)的集合,范數(shù)定義為本文工作空間,它的對偶空間記為(X′,‖·‖X′),在X上賦予范數(shù)‖·‖X=‖·‖H+|·|∞.在本文中,Ci,i ∈{1,2,3,···},表示正常數(shù),εn表示當(dāng)n →∞時(shí)的無窮小量,εk,n表示與k有關(guān)的當(dāng)n →∞時(shí)的無窮小量.
定義2.1設(shè)Z是Banach空間,泛函I在Z上的Frechet導(dǎo)數(shù)dI存在,稱序列{un} ?Z是I的一個(gè)(CPS)c序列,如果該序列滿足
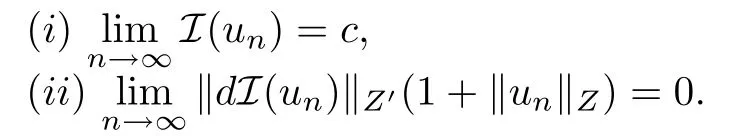
定義2.2設(shè)Z是Banach空間,若存在Banach空間(B,‖·‖B),使得(連續(xù)嵌入).稱泛函I在水平c上滿足(wCPS)c條件,如果對于I的每個(gè)(CPS)c序列{un} ?Z,都存在{un}的子列(仍記為{un})以及u ∈Z,使得
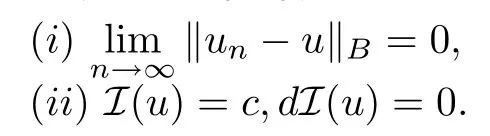
因?yàn)?wCPS)c條件(i)只表明在‖·‖B意義下的收斂,故I的臨界點(diǎn)集在‖·‖B意義下是緊的,但在‖·‖Z意義下不能保證是緊的.幸運(yùn)的是,在這個(gè)弱條件下,形變引理和一些臨界點(diǎn)定理仍然成立[6-7].
定理2.1(山路引理) 設(shè)Z是Banach空間,且存在Banach空間(B,‖·‖B),使得.泛函I ∈C1(Z,R),I(0)=0,滿足(wCPS)c條件,且存在正常數(shù)r0,ρ0,存在點(diǎn)e ∈Z,且
(i) 當(dāng)u ∈Z,且‖u‖B=r0時(shí),有I(u)≥ρ0,
(ii)‖e‖B >r0,且I(e)<ρ0,
則I有一個(gè)山路臨界點(diǎn)u* ∈Z,且I(u*)≥ρ0.
定理2.2(對稱山路定理) 設(shè)Z是Banach空間,且存在Banach空間(B,‖·‖B),使得.設(shè)I ∈C1(Z,R)是偶泛函,滿足(wCPS)c條件,I(0)=0.存在ρ >0,使得
(i)存在Z的閉子集Vρ和Wρ,滿足
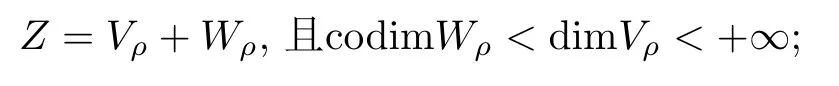
(ii)存在常數(shù)rρ >0,當(dāng)u ∈Wρ,且‖u‖B=rρ時(shí),有I(u)≥ρ;
(iii)存在常數(shù)Rρ >0,當(dāng)u ∈Vρ,且‖u‖Z ≥Rρ時(shí),有I(u)≤0.
則I在Z內(nèi)至少有一對臨界點(diǎn),且臨界值位于
注記2.1記Γρ={γ:Z →Z |γ是一個(gè)奇的連續(xù)映射,當(dāng)u ∈Vρ且‖u‖Z ≥Rρ時(shí),γ(u)=u},根據(jù)文獻(xiàn)[6],對γ ∈Γρ有
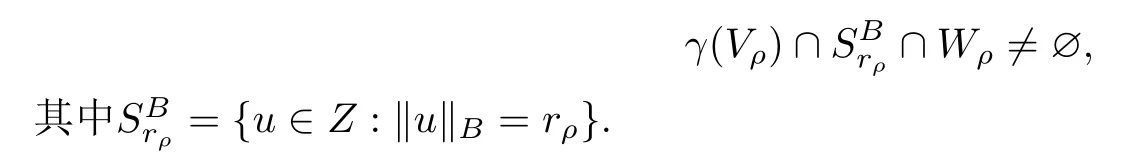
下面給出可以獲得序列在空間強(qiáng)收斂的引理.
引理2.1[20]設(shè)W是一致凸的Banach空間,算子A ∈C(W,W′),且對任意的u,v ∈W,存在正常數(shù)a,成立

其中p ∈(1,+∞).如果當(dāng)j →+∞時(shí)序列{uj}?W滿足
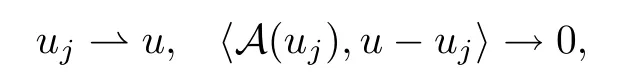
則{uj}在W中有強(qiáng)收斂子列.
下面的引理將保證在某些條件下W1,p(Ω)中函數(shù)的有界性.
引理2.2[6]設(shè)Ω是RN內(nèi)的有界區(qū)域,且有光滑邊界?Ω.對于v ∈W1,p(Ω)(1≤p ≤N),如果存在b >0和k0∈N使得

§3 泛函J 的正則性
容易證明,在空間X上,泛函J的Gateaux導(dǎo)數(shù)為
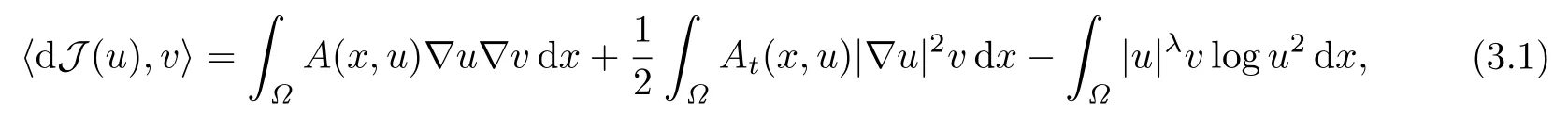
且dJ是泛函J的Frechet導(dǎo)數(shù),dJ在‖·‖H意義下是連續(xù)的.
引理3.1設(shè)u ∈X,{un} ?X,|un|∞<M,且當(dāng)n →∞時(shí),‖un -u‖H →0,則成立|J(un)-J(u)|→0和‖dJ(un)-dJ(u)‖X′ →0.
證記
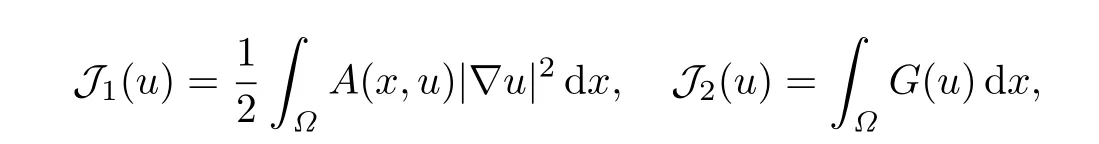
則J=J1-J2.由注記1.3,J2在X上是C1的,因此只要分析J1的連續(xù)性和可微性.
設(shè){un}是滿足條件的序列,由于
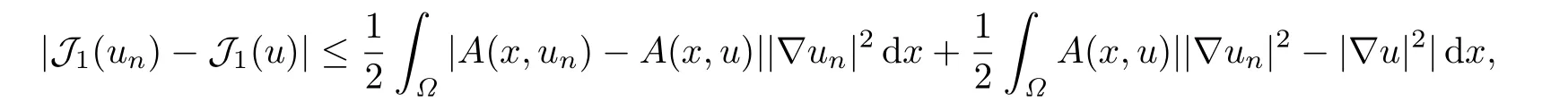
根據(jù)|un|∞<M以及(A0),(A1),那么存在正常數(shù)C6,使得
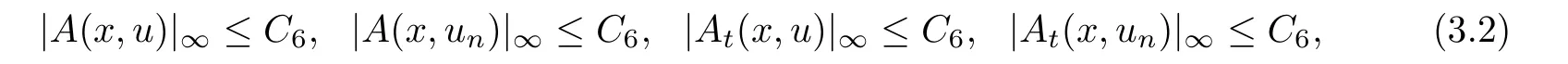
且當(dāng)n →∞時(shí),有un →ua.e.x ∈Ω.利用(3.2),‖un-u‖H →0和Lebesgue控制收斂定理可得
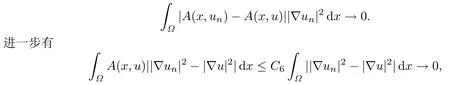
即|J1(un)-J1(u)|→0,故泛函J1是連續(xù)的.
另一方面,對任意v ∈X,且‖v‖X=1,有
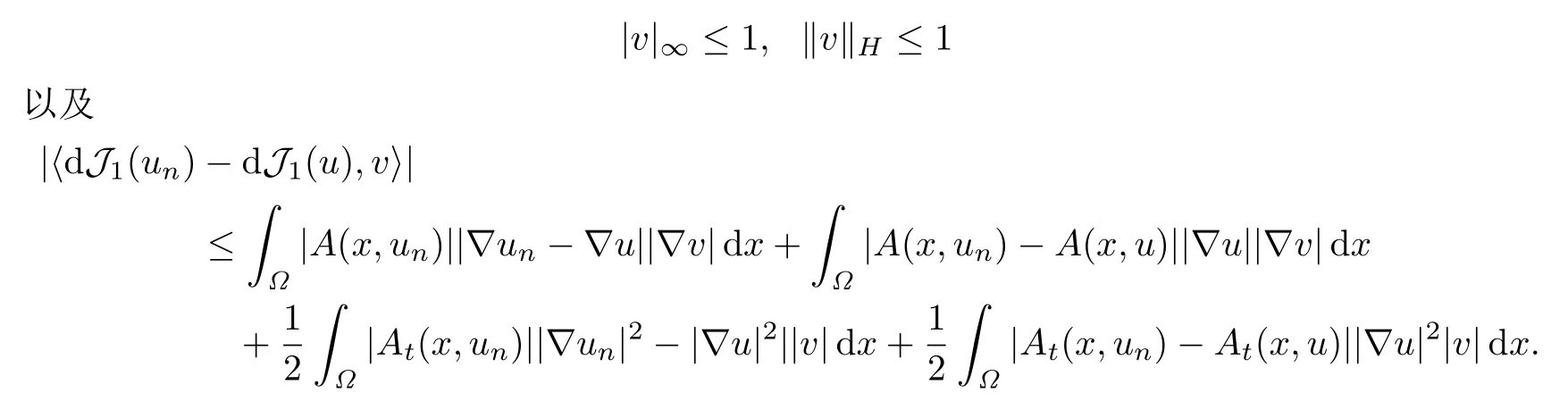
因?yàn)椤瑄n-u‖H →0,由式(3.2),利用H?lder不等式和Lebesgue控制收斂定理,可得
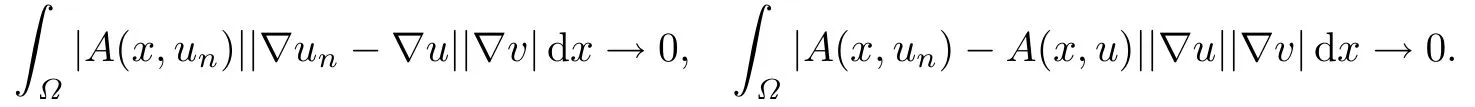
重復(fù)證明J1連續(xù)性的步驟,可得

綜合分析可知,對任意v ∈X,且‖v‖X=1,當(dāng)n →∞時(shí),有|〈dJ1(un)-dJ1(u),v〉| →0一致成立,故‖dJ1(un)-dJ1(u)‖X′ →0.
§4 山路解的存在性
引理4.1設(shè)N ≥2,λ ∈(1,2*-1),A(x,t)滿足條件(A0)-(A4),則對任意c ∈R,泛函J滿足(wCPS)c條件.
證對c ∈R,設(shè){un}?X為J的(CPS)c序列,即
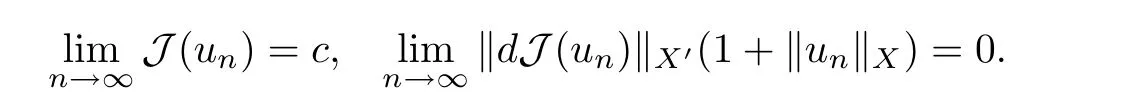
Step 1證明{un}在(Ω)上是有界的.
由于
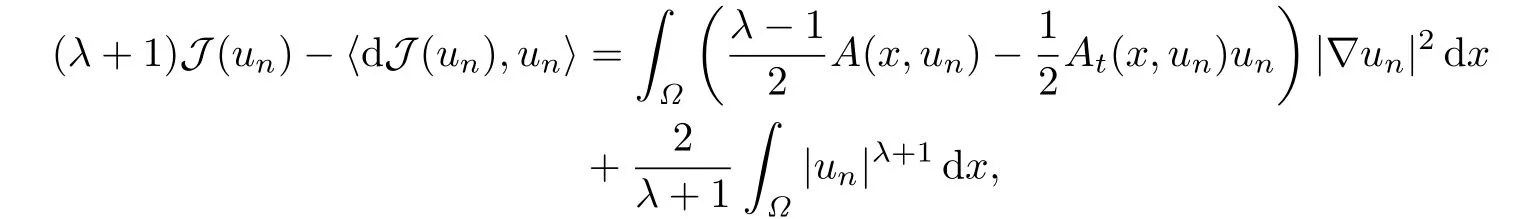
結(jié)合(A2),(A3),從上式可得
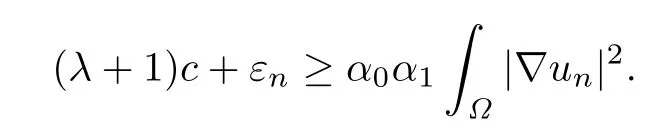
因此{(lán)un}在(Ω)上有界,故存在{un}的子列(仍記為其本身)及(Ω),當(dāng)n →∞時(shí)有
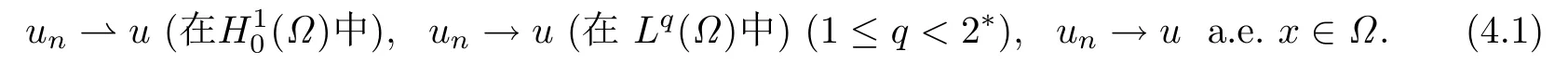
Step 2證明u ∈L∞(Ω).
反證,如果uL∞(Ω),則有
若第一種情況成立,則對于固定的k ∈N,k >R0(R0由(A4)給出),有meas()>0,其中.定義,考慮函數(shù)

故存在nk ∈N,當(dāng)n ≥nk時(shí),有
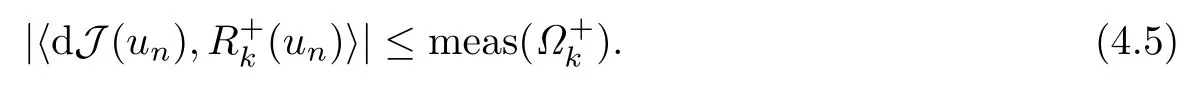
利用(A4)可得
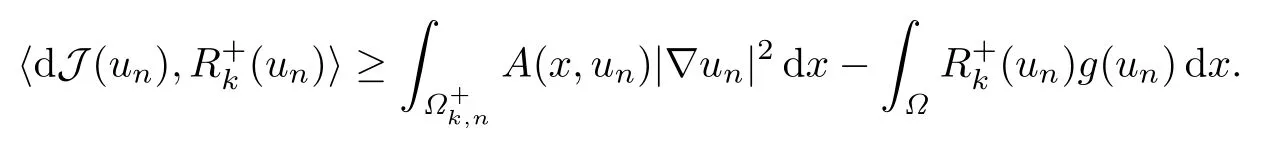
進(jìn)而利用(A2),有

注記1.3表明
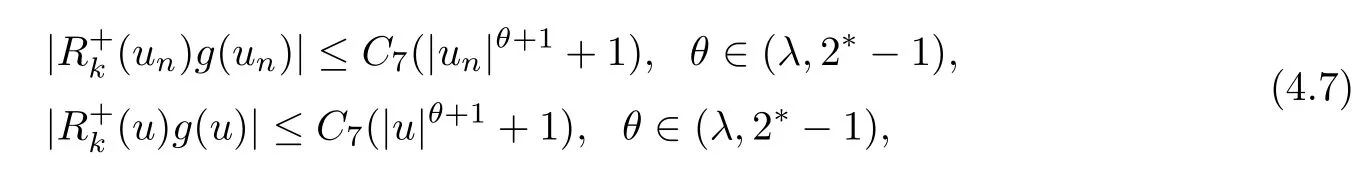
從而利用Lebesgue控制收斂定理有
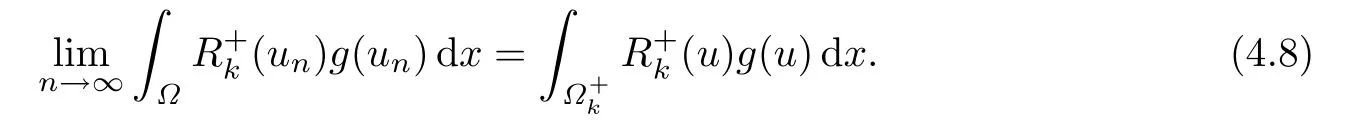
由(4.2)-(4.8),可得

由于上式對所有k >R0都成立,利用引理2.2便得到矛盾.因此第一種情況不成立.
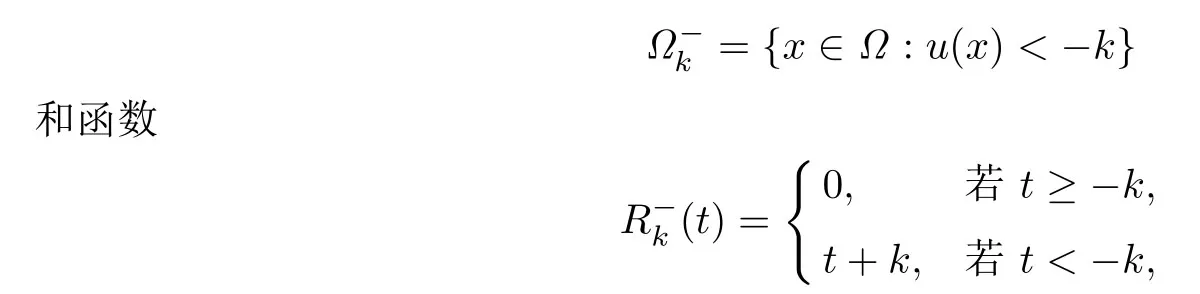
重復(fù)以上步驟,同樣可以得到矛盾.因此第二種情況也不成立,故u ∈L∞(Ω).
Step 3構(gòu)造新的(CPS)c序列.
定義函數(shù)Tk:R→R

下面證明當(dāng)k ≥max{|u|∞,R0}+1時(shí),{Tk(un)}也是(CPS)c序列.
定義Ωk={x ∈Ω:|u(x)|>k}和Ωk,n={x ∈Ω:|un(x)|>k},由函數(shù)Tk的定義可得

因?yàn)閗 >|u|∞,所以有
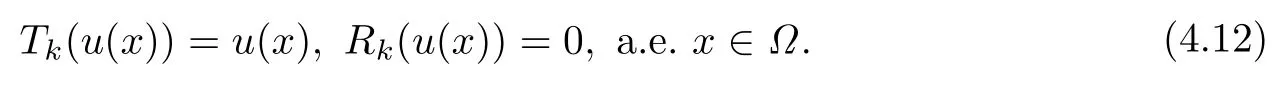
再由(4.1),當(dāng)n →∞時(shí),有
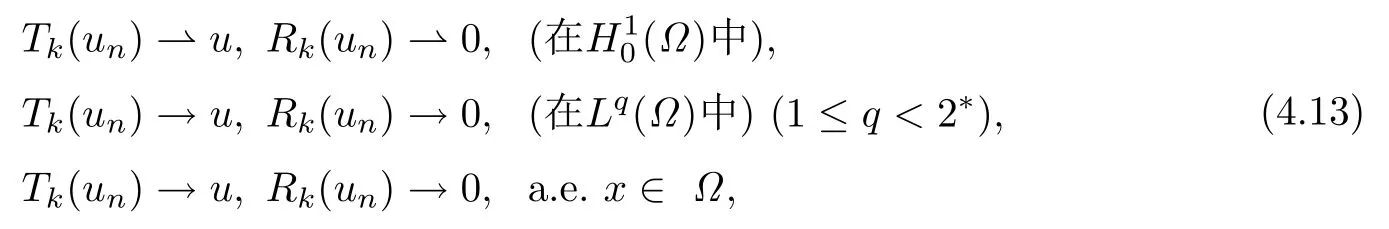
且由k >|u|∞可得
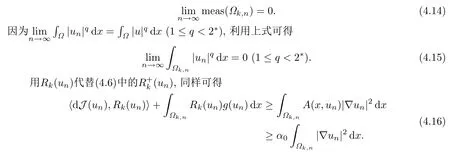
從(4.14)和(4.15)有
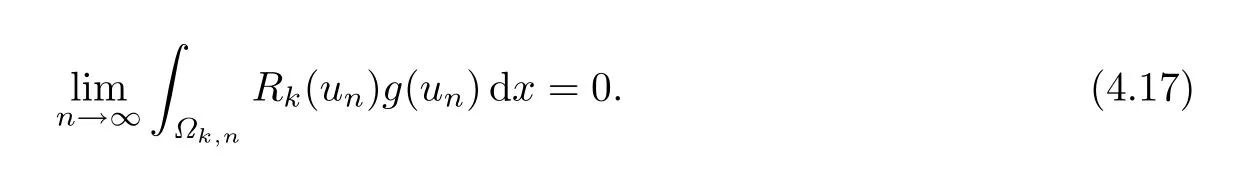
由(4.11)有
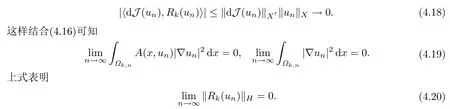
根據(jù)Tk(un)的定義有

利用(4.14),(4.15)和注記1.3得到
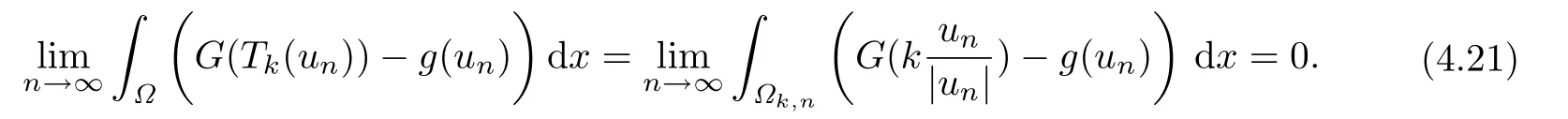
結(jié)合(4.19)可知
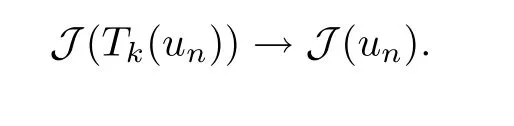
任取v ∈X,且滿足‖v‖X=1,有
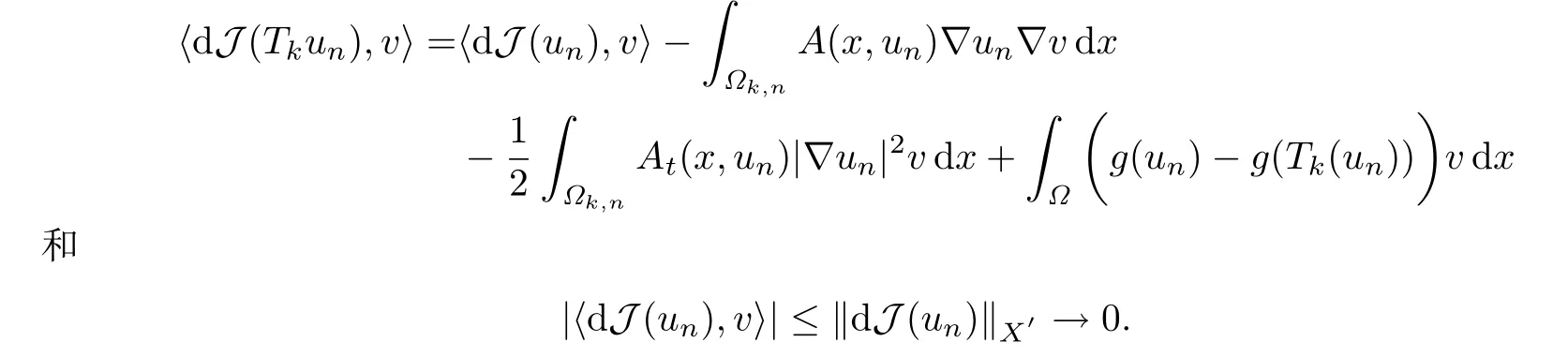
運(yùn)用類似于證明(4.21)的方法可得

注意到v ∈L∞(Ω),綜合(4.19),(4.12)和(4.8)可得
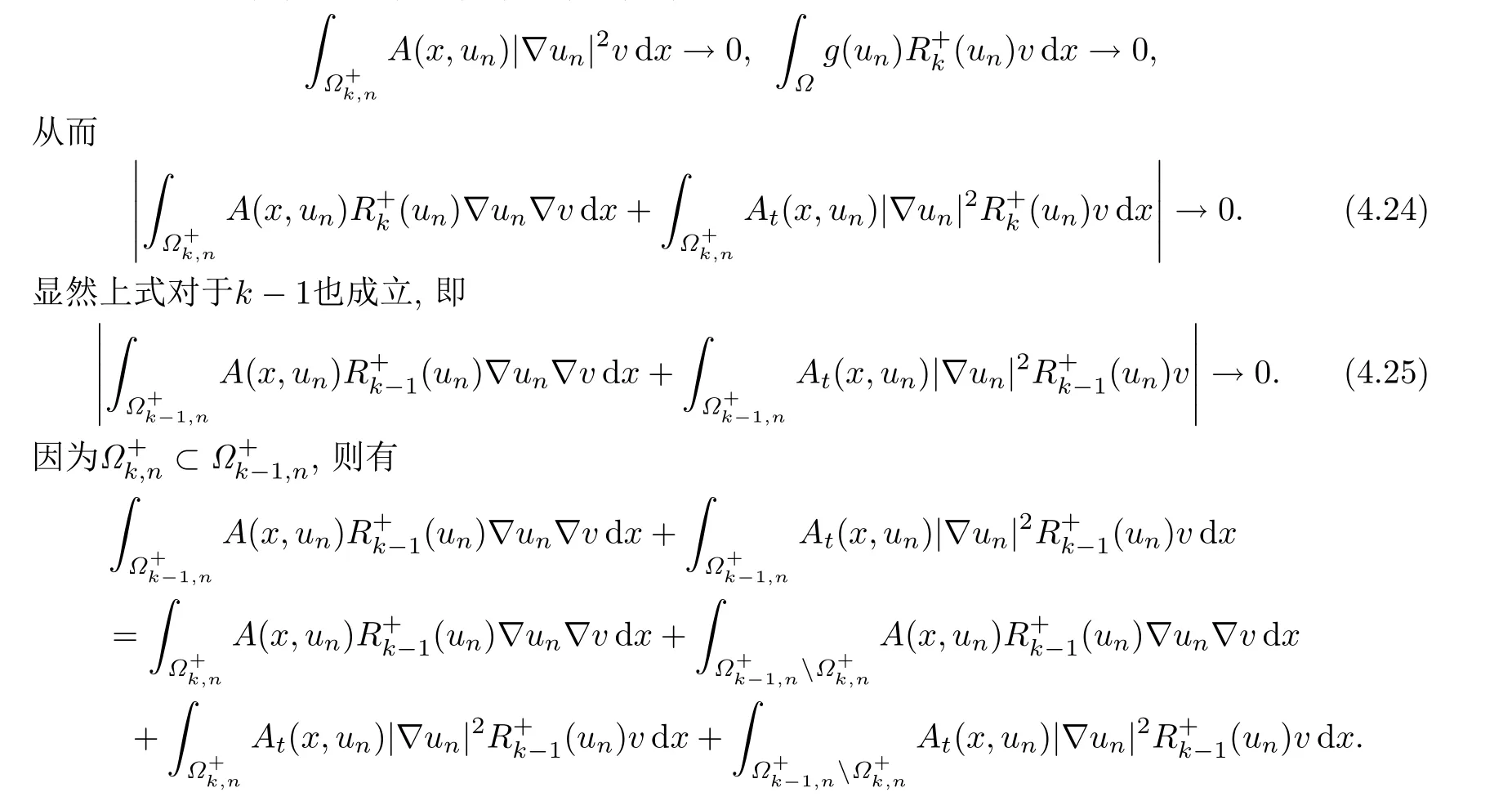

由(4.23),當(dāng)n →∞時(shí),有〈dJ(Tk(un)),v〉→0,所以序列Tk(un)是J的(CPS)c序列.
Step 4證明當(dāng)n →∞時(shí),有‖Tk(un)-u‖H →0和‖un-u‖H →0.
定義函數(shù)
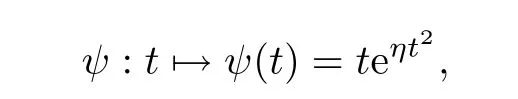

定義函數(shù)vk,n=Tk(un)-u,由(4.10)和|u|∞<k,知|vk,n|∞<2k.由ψ的定義和(4.13),當(dāng)n →∞時(shí)有


根據(jù)Step 2的結(jié)論,可得
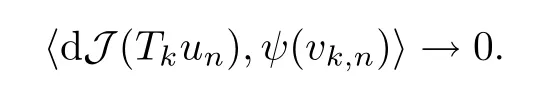
由(4.10),(4.27),(4.28)和注記1.3,利用Lebesgue控制收斂定理有

在Ω Ωk,n上,有|un(x)|≤ka.e.x ∈Ω,由條件(A1)和(A2)則有

由條件(A1)和(4.27),利用H?lder不等式和Lebesgue控制收斂定理可得

根據(jù){un}和{vk,n}在(Ω)上的有界性,以及{A(x,un)}在Ω Ωk,n上有界,運(yùn)用(A1),H?lder不等式和Lebesgue控制收斂定理可得
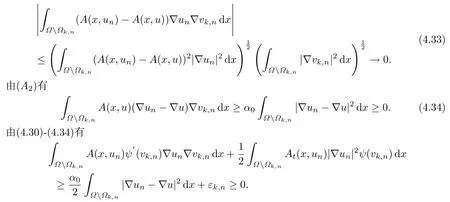
結(jié)合(4.29)可得

對(Ω),定義算子L(u)滿足
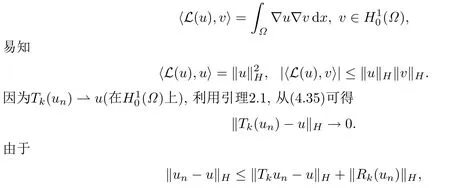
結(jié)合(4.20),當(dāng)n →∞時(shí)有
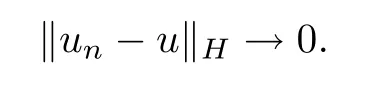
Step 5證明J(u)=c,dJ(u)=0.
由上述討論可知,當(dāng)k充分大時(shí),{Tk(un)}是(CPS)c序列,且對所有n ∈N,有|Tk(un)|∞≤k,‖Tk(un)-u‖H →0,由引理3.1可知J(u)=c,dJ(u)=0.
引理4.2設(shè)N ≥2,λ ∈(1,2*-1),A(x,t)滿足(A0)-(A4),則泛函J滿足山路引理的幾何條件.
證由(A2),(1.12)和嵌入不等式有
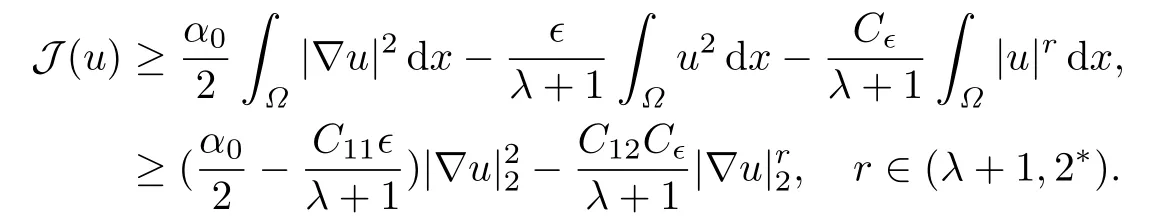
取∈足夠小,使得,故|?u|2充分小時(shí),即‖u‖H充分小時(shí),就有J(u)>0.
設(shè)φ1為(-Δ,(Ω))的第一特征函數(shù),不妨設(shè)φ1>0,由注記1.2,對s >0有

結(jié)合引理4.1和引理4.2,根據(jù)定理2.1知,J存在一個(gè)山路臨界點(diǎn),故問題(1.1)存在一個(gè)非平凡解,即定理1.1 得證.
§5 解的多重性

引理5.1對X的任意有限維子空間V,都存在R >0,當(dāng)u ∈V,且‖u‖X ≥R時(shí),有J(u)≤0,并且J在V內(nèi)是上有界的.
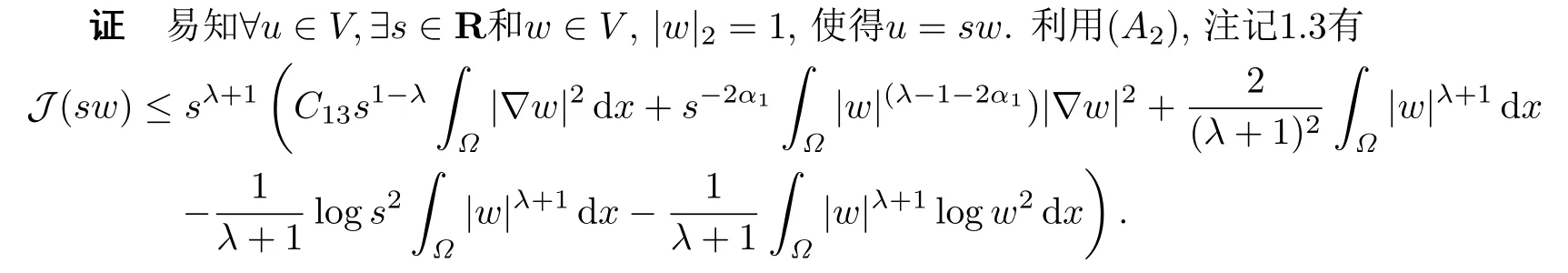
由于有限維空間所有范數(shù)是等價(jià)的,故上面關(guān)于w的所有積分都是有界的.又λ >1,α1>0,因此當(dāng)s →+∞時(shí),J(sw)→-∞,故存在R >0,當(dāng)‖u‖X ≥R時(shí),有J(u)≤0.
引理5.2對于任意給定ρ >0,則存在m ∈N和rm >0,當(dāng),且‖u‖H=rm時(shí),有J(u)≥ρ.
證從(A2)和注記1.3可得
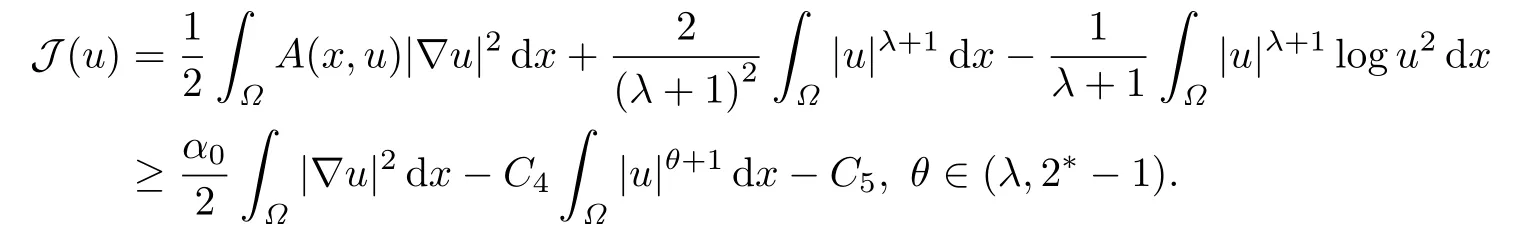
記β=θ+1,選擇r ∈(0,β)滿足,由插值不等式和,則

易知J是偶泛函.對給定ρ0,由引理5.2知存在m0∈N和rm0>0,當(dāng),且‖u‖H=rm0時(shí),有J(u)≥ρ0.對于任意m1>m0,顯然有codimHm0<dimVm1,則由引理5.1,注記2.1,定理2.2,可得J存在一對臨界點(diǎn),且臨界值位于區(qū)間[ρ0,ρ1],其中選取新的,重復(fù)上述過程,可以找到另一對臨界點(diǎn),從而問題(1.1) 有無窮多個(gè)非平凡解.至此,定理1.2得證.

