Current carrying states in the disordered quantum anomalous Hall effect

Yi-Ming Dai(戴鎰明) Si-Si Wang(王思思) Yan Yu(禹言) Ji-Huan Guan(關(guān)濟(jì)寰)Hui-Hui Wang(王慧慧) and Yan-Yang Zhang(張艷陽)

1School of Physics and Materials Science,Guangzhou University,Guangzhou 510006,China

2Research Center for Advanced Information Materials,Guangzhou University,Guangzhou 510006,China

3School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China

4SKLSM,Institute of Semiconductors,Chinese Academy of Sciences,Beijing 100083,China

5School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

6Beijing Academy of Quantum Information Sciences,Beijing 100193,China

7Huangpu Research and Graduate School of Guangzhou University,Guangzhou 510700,China

Keywords: quantum anomalous Hall effect,Chern number,disordered system,localization

1. Introduction

A Chern insulator is a two-dimensional (2D) material without time reversal symmetry, whose occupied bands possess a nonzero Chern number.[1,2]This Chern number gives rise to topological edge states in the bulk gap, leading to robust transports against weak disorder. The earliest example is the integer quantum Hall (IQH) effect in an external magnetic field, where energy bands are flat and highly degenerate Landau levels.[3]Disorder introduces localized states and broadens Landau levels.Taking states associated with nonzero Chern number as current carrying(CC) or delocalized states,previous numerical studies show that in the thermodynamic limit, these CC states shrink into one single energy value in each disorder broadened Landau level.[4-7]In the presence of a random magnetic field, it takes some endeavors to understand that a similar picture holds.[7-9]

Quantum anomalous Hall (QAH) effect corresponds to a Chern insulator without an external magnetic field, which was firstly proposed by Haldane[10]and realized in recent years.[11-15]In the clean limit, instead of flat Landau levels in IQH systems, the energy bands of a QAH system are dispersive and with finite widths. With increasing disorder, the global route towards localization of QHE effects in the transport picture has been investigated extensively.[16-19]Very recent researches shed light on the difference of localization between QAH and IQH effects.[19,20]However,a detailed picture of CC states is not clear so far,for example,their distributions and evolutions under increasing disorder. Moreover, at weak disorder,will the spectrum width of CC states within each dispersive bulk band still vanish in the thermodynamic limit?

To resolve these issues,in this manuscript,we perform a numerical investigation on a disordered two-band QHA lattice model with Chern number 1. Based on a real space method of evaluating Chern numbers, we study the picture of CC states before localization through size scaling. We find that,in spite of dispersive bulk bands with finite width, the CC states also shrink into a single energy value in the thermodynamic limit.The rate of shrinking during size scaling depends on the disorder strength. At the intermediate disorder,it is equal to that found in the IQH effect.[4]

2. Model and method

Fig.1. (a)The band structure of a ribbon geometry with width Ny=40 and open boundary condition. (b)Chern number at Fermi energyμ=0 as a function of disorder strength W,for different sample sizes Nx×Nx.All data are averaged over at least 100 disorder configurations. The model parameters are: A=0.3,B=0.2,D=0,M=0.2,which will be used throughout this manuscript.

In real space, the effect of disorder is included as a random potential term to the Hamiltonian as

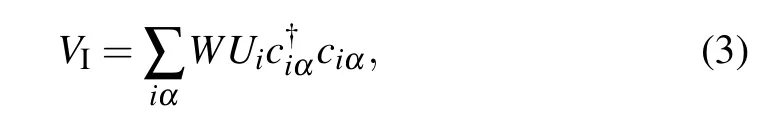
whereUiare independent random numbers uniformly distributed in(-0.5,0.5)andWis the disorder strength.

Topological invariants are usually conveniently defined in the momentum space.[1,2,24,26,27]However here, disorder destroys the translation invariant symmetry. Therefore it is more convenient to investigate this problem in the real space. For a disordered finite-size system,our evaluation of Chern numbers is based on the real space algorithm of the topological marker at positionr=(x,y)and Fermi energyμ[28,29]

whereP= ∑εn＜μ|ψn〉〈ψn| is the projector over occupied eigenstates{|ψn〉}of the Hamiltonian, andQ= 1-P. It has been argued that its value at the sample center tends to be the Chern number at thermodynamic limit.[29,30]Taking each energy level as the Fermi level one by one,we can associate a quantized Chern number to each level based on reasonable considerations. Details of this calculation are described in the Appendix. Following previous spirits and definitions in Refs. [4,5,7,31], we take the eigenstates associated with nonzero Chern numbers as CC states, which play the role as delocalized states. Then, the Chern number resolved density of states(DOS)is defined to be[4,31]

where the sum is over energy levels associated with the same Chern numberC. Hereafter in this manuscript,all finite samples are square shaped with lattice sitesN ≡Nx×Nx.

For a Chern number resolved DOS, the spectrum width ΔEalong the energy axis is a key property. In the pioneer work,[4]this was defined as the standard deviation of the energy level distribution. This was suitable there because their calculations were strictly restricted within the lowest Landau level alone.[4]Here however, we are facing a lattice model with two bands,and disorder may generate more subbands as sub-peaks of DOS[see,e.g.,Fig.3(b)]. In this case,the standard deviation over the whole energy is not a good definition as ΔEof a certain band or peak,since far sub-peaks will contribute remarkable but unwanted standard deviation. Instead,we adopt the width at half height of the main peak as the spectrum width ΔEhere.

3. Results

In Fig.1(b),we plot the disorder averaged Chern numberCas a function of disorder strengthW, for different sample sizesN ≡Nx×Nx,which is evaluated at Fermi energyμ=0.Here and in the rest of this paper,we check the convergence of the averaging by adopting sufficiently number of disorder samples,which is the most time consuming part of this work. The Chern number is a well quantized plateau whenW1,reflecting the robustness of a topological phase against weak disorder. We call this range the Chern number plateau region. After that,the quantization starts to collapse successively,at a largerWfor a larger size.Finally strong disorder leads the system towards an Anderson localization withC=0 afterW2.5. All four curves associated with different sizes cross atWc=2.1,suggesting a critical point of disorder induced topological transition at the thermodynamic limit,N →∞.[16,32]Although the transition at infinite size is a single pointWc=2.1, we call the rangeW ∈(1,2.1)the transition region because the Chern number plateau has collapsed for all finite sizes we calculate here. This will give rise to some finite size effects in the following. Since the main interests of this manuscript is the CC or delocalized states, our focus will be situations before the complete localization,i.e.,W ＜Wc.

Now we investigate this process in the picture of CC states. In Fig. 2, we show the Chern number resolved DOS as defined in Eq. (5), which are also averaged over disorder ensembles,for different disorder strengths. From the DOS of localized states(associated withC=0)in Figs.2(a)-2(e),one can see that disorder expands both bands along the energy axis,and the bulk gap is filled gradually.In Figs.2(f)-2(j),the DOS of delocalized states,i.e.,CC states associated withC/=0 offers more information. In the clean limit, two bands possess opposite Chern numbers respectively. With increasing disorder, their centers of mass approach towards each other. Then these two opposite Chern numbers touch, merge and finally annihilate into topologically trivial states. This picture is consistent with previous studies.[16,17,32]

Fig. 2. Chern number resolved DOS ρC at different disorder strength W. The left(right)column corresponds to zero(nonzero)Chern numbers. Black,red and blue curves are for Chern numbers 0,-1 and+1 respectively. All data are calculated with the sample size N =20×20 and averaged over 1000 disorder configurations.

The above result was for a finite size sample (20×20),where the spectrum of CC states seemed to be broad and finite. Now we study their tendency during size scaling. In each dispersive band, will the CC states shrink to a single energy point in the thermodynamic limit as well?

To answer this question, we need to scrutinize the size dependence. Figure 3 presents the Chern number resolved DOS at a fixed weak disorder strengthW=0.7 (well before theC=1 plateau collapses)with different sizes,for localized(C=0) (a), and CC (C/=0) states (b), respectively. We first notice remarkably different energy scales in these two panels.This suggests that,for sufficiently large sizes,there are much more CC states than localized states. With increasing size,these two types of states exhibit different dependence on the size scaling.For the localized states[Fig.3(a)],the DOS spectrum is almost unaffected. On the contrary,the main peaks of CC states [Fig. 3(b)] become sharper and narrower with size scaling, for both valance and conduction bands. This result implies that, although the band widths of QAH effect are finite at weak disorder, the spectrum widths of CC states still tend to be very narrow in the thermodynamic limit.

Fig. 3. Chern number resolved DOS ρC for different sample sizes Nx×Nx, at a definite disorder strength W = 0.7, (a) for zero Chern number and,(b)for nonzero Chern numbers. All data are averaged over at least 100 disorder configurations.

To see this narrowing in a more quantitative way,we show the log-log plot between the spectrum width of CC states ΔEand the sample sizeN ≡Nx×Nxin Figs.4(a)and 4(b),in the Chern number plateau regionW ≤1, well before the disorder induced localization. For both Chern numbers,C=±1,approximate linearities suggest that the scaling relation is a power law

wherexis determined by the absolute value of the slope in this figure. This is similar to the case of IQH effect.[4]In other words, in each bulk band of a disordered QAH system, although the total band width is finite, all extended states (CC states) within this bulk band still shrink to a single energy point in the thermodynamic limit. We call this energy point of CC states as the topological center(TC)of each band. All other bulk states around the TC are localized, which will be called bulk localized states in the following, since their presence and properties do not depend on the situation of boundary conditions. Such a broad distribution of localized states is not surprising for a 2D system.[33]

This leads to a picture illustrated as follows. In a disordered QAH system at the thermodynamic limit, there is one TC in each bulk band, with opposite-sign Chern numbers for the valence and conduction bands respectively. Since they are CC states, there will always be topological induced currents when the Fermi energy is between them. From the topological view this is not surprising because in the presence of edges,topological edge states always connect TCs with opposite Chern numbers.[24]In the bulk gap without any bulk states,they give rise to a quantized and robust Hall conductance. On the other hand,inevitably,some edge states will traverse bulk localized states around topological centers. If some of these bulk localized states are sufficiently flat, then edge states can exhibit their quantized transports in subgaps between these flat localized states. This is consistent with our previous observations in disordered 2D topological insulators,[34]where for the quantized conductance plateau,the larger portion is a topological Anderson insulator(edge states living in a mobility gap),instead of a topological band insulator(edge states living in an energy gap).

Fig.4. Characteristic quantities of CC states as functions of sample size N ≡Nx×Nx in double logarithm scales. (a)and(b)Spectrum width of CC DOS peak ΔE. (c)and(d)Number of CC states Nc. The upper(lower)row is for Chern number C=1(C=-1).

Besides the spectrum width ΔE, another aspect of CC states is their numberNcwith respect to the scaling of sizeN. In Figs. 4(c) and 4(d), we present the log-log plot of this relation. Again, the linearities suggest a power law between them as

where the exponent is determined by the slopes of lines in Figs.5(c)and 5(d).

In Fig.5,we present the dependence of exponentsxandy(solid dotted lines) on the disorder strengthW. The dependence is weak and all curves seem to be constant approximately, especially in the plateau region with weak disorderW ＜1. We attribute the irregular fluctuations to disorders at finite sizes.At the intermediate disorder,the exponentx～0.2,close to that found in IQH systems.[4]Moreover,the sumx+y(dashed lines in Fig.5)tends to be～1.1. This was found to be 1 in IQH systems, so that the CC DOS at the TC can be finite.[4]We believe this should also be the case here in the thermodynamic limit,because we have checked that for larger sample sizes, and this sum is really closer to 1. Again, the discrepancy may come from strong disorder fluctuations and finite size effects of lattice models. For example, as one can see from Fig. 1(b), although the critical disorder strength is believed to beWc～2.1 in the thermodynamic limit,the averaged Chern numbers have lost their quantization afterW～1.5,for all sample sizes within our calculation capability. This will lead to remarkable finite size effects,and some subsequent statistical uncertainties exhibited in Figs.4 and 5.

Fig.5. Size scaling exponents of CC states with C=±1 as functions of the disorder strength W: x defined in Eq. (6) for the spectrum width ΔE, and y defined in Eq. (7) for the number of CC states. Dashed lines are their sums x+y.

4. Summary

As a summary, we numerically investigate the CC states in a disordered QAH system. Performing the finite-size scaling,we conclude that within the dispersive bulk band,all CC states converge to a single energy value, similar to what happens in disorder broadened Landau levels of an IQH system.At the intermediate disorder,the shrinking rate of the spectrum width of CC states is close to that in the IQH system. This is consistent with the previous picture that the topological Anderson insulator constitutes a large portion of the quantized conductance plateau in the presence of disorder.

Appendix A: Real space representation of the BHZ model

Here we present the derivation of BHZ model of spin-up part in real space. In the momentum space,the spin-up part of the BHZ Hamiltonian reads[21]

Appendix B: Numerical evaluation of Chern numbers

In this Appendix, we introduce how to associate a quantized Chern numbers to each energy level of a finite size system, based on the real space algorithm of the topological marker.[28]Consider a finite size tight-binding model with totalNorbitals (and thereforeNenergy levels). If the Fermi level isEn, i.e., the energy levels are occupied up to then-th one, then the ground state projectorPand its complementQare defined as[28-30]

So far,the Chern number,as well as the Chern marker,is associated with the occupied states as a whole. On the other hand,the current carrying states are defined to be energy levels with nonzero Chern numbers, so one needs to associate each level with a quantized Chern number. For example, we need to investigate the density of states(DOS)from different Chern numbers separately,[4-7,31]i.e.,Eq.(5).

However,for a generic Fermi levelEnof a finite size system,the ground-state Chern markerCnmay deviate from integer remarkably.This corresponds to the case that the Fermi energy is within a subband(consisting of a cluster of consecutive energy levels, which will be explained in the following) and therefore the integrated Berry curvature is not quantized.[24]As a result,a quantized Chern number can only be defined to a cluster of consecutive energy levels which constitute a physical subband, instead of to a single level. In our numerical calculations,as illustrated in Fig.B1,we first search all levelsEnr(r=1,2,...andn1≡1)at which the ground state Chern markerCnris well quantized,i.e.,the deviation ofCnrfrom an integer is smaller than a tolerance errorε. Then,with two adjacent quantization levels as the upper and lower band boundary respectively, a subband consisting of all levels between them can be well defined. Consequently, a quantized Chern number can be naturally attributed to this subband. In other words,now levels with indices fromnr-1+1 tonrconstitute a subband possessing Chern numberC(r)≡Cnr-Cnr-1, and all these levels contribute toρC(r)(E)in Eq.(5). We call these levels as “associated with Chern numberC”. Notice the difference between notationsCnandC(r). The notationCncorresponds to the Chern marker associated with the lowestnlevels,whileC(r)corresponds to the Chern number(which has been defined to be quantized)associated with ther-th subband.

Fig. B1. Illustration of associating a quantized Chern number to discrete energy levels. All quantization levels Enr are picked out where the ground state Chern marker Cnr are quantized. Then levels from Enr-1 +1 to Enr are defined to be the r-th subband with a quantized Chern number C(r)≡Cnr-1-Cnr.

This picture of a subband (on which a quantized Chern number can be defined)is equivalent to that defined in the momentum space of disordered supercells, with the momentum running over the disorder folded Brillioun zone.[16,35]It should be noted that, although subgaps between these subbands are finite for a certain finite-size sample, most of them will vanish after disorder average and in/or the thermodynamic limit.Only the gap survives after these two processes is a “truly”physical gap. Correspondingly, a truly physical band (which may consists of many subbands)is the set of all energy levels between two physical gaps.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11774336, 12104108, and 61427901) and the Starting Research Fund from Guangzhou University(Grant Nos.RQ2020082 and 62104360).