Reflection-based traveltime and waveform inversion with secondorder optimization
Teng-Fei Wang , Jiu-Bing Cheng ,*, Jian-Hua Geng
a State Key Laboratory of Marine Geology, Tongji University, Shanghai, 200092, China
b School of Ocean and Earth Science, Tongji University, Shanghai, 200092, China
Keywords:Reflection waveform inversion Reflection traveltime inversion Gauss-Newton Hessian
ABSTRACT Reflection-based inversion that aims to reconstruct the low-to-intermediate wavenumbers of the subsurface model, can be a complementary to refraction-data-driven full-waveform inversion (FWI), especially for the deep target area where diving waves cannot be acquired at the surface. Nevertheless, as a typical nonlinear inverse problem, reflection waveform inversion may easily suffer from the cycleskipping issue and have a slow convergence rate, if gradient-based first-order optimization methods are used. To improve the accuracy and convergence rate, we introduce the Hessian operator into reflection traveltime inversion (RTI) and reflection waveform inversion (RWI) in the framework of second-order optimization. A practical two-stage workflow is proposed to build the velocity model, in which Gauss-Newton RTI is first applied to mitigate the cycle-skipping problem and then Gauss-Newton RWI is employed to enhance the model resolution.To make the Gauss-Newton iterations more efficiently and robustly for large-scale applications, we introduce proper preconditioning for the Hessian matrix and design appropriate strategies to reduce the computational costs. The example of a real dataset from East China Sea demonstrates that the cascaded Hessian-based RTI and RWI have good potential to improve velocity model building and seismic imaging, especially for the deep targets.
1. Introduction
Complex heterogeneities naturally existing in the Earth’s subsurface lead to the spatial variations of the elastic properties,such as velocity, density and so on. Seismic wavefield propagates in the subsurface and carries important elastic responses that can be used for seismic imaging. In the exploration seismology,seismic tomography and imaging methods are employed to estimate the subsurface elastic properties, with which the type of pore fluid or the distribution of stress field can be predicted for the purpose of hydrocarbon reservoir exploration and geotechnical engineering.
Exploration seismic imaging is practically applied based on a scale separation of velocity model,i.e.,a smooth background and a rough perturbation (Claerbout,1971). The smooth background velocity is first estimated by the migration velocity analysis(MVA)or ray-based traveltime tomography and then the rough perturbation is obtained by the migration process (Claerbout, 1985). Over the past decades,one of the most important tasks for seismic imaging is to reconstruct a background velocity model that can correctly honor the kinematics of the wave propagation. The standard velocity model building for prestack-depth-migration (PSDM) is based on the reflection traveltime tomography with ray-tracing,in which the migration velocity model is iteratively updated by backprojecting the residual depth or moveout (RMO) on the common image gathers (CIGs) along the ray path (Stork, 1992; Wang and Pratt,1997; Woodward, 2008). Due to the limitation of ray-based theory, the PSDM-based reflection traveltime tomography easily fails in the presence of complex velocity variation and lead to inaccurate imaging of the target. Besides, the generation of CIGs during the PSDM and the picking of RMO are quite expensive and clumsy to support multifold iterations of velocity model building(Alder et al., 2008; Guillum et al., 2008).
To overcome the limitation of ray-based method, waveequation-based migration and tomography techniques, such as reverse-time migration (RTM) and full-waveform inversion (FWI),have been proved quite effective to improve the accuracy of seismic imaging (Virieux and Operto, 2009; Zhang et al., 2014). Nevertheless, FWI easily suffers from the cycle-skipping problems when starting model is poor and/or low frequency data is unavailable.Therefore, as a model building process, FWI only provides robust velocity update for the shallow part of the model where turning waves are sufficiently available. The velocity update in the deep part remains to be improved, especially in the field data applications. Xu et al. (2012) introduced wave-equation reflection waveform inversion (RWI) which aims to recover the background velocity by minimizing the waveform misfit between synthetic and observed reflections. In the context of wave-equation reflection tomography or waveform inversion, sharp contrasts of the elastic properties or reflectivity in the subsurface medium are prerequisite(provided by seismic migration), with which the reflection wavefields are generated to produce the tomographic misfit kernels(“rabbit-ear”) connecting the shots and receivers to the reflectors.In the past few years, RWI becomes a quite promising method to recover the low-to-intermediate wavenumber components of the velocity model (Zhou et al., 2015; Wu and Alkhalifah, 2015; Wang and Cheng, 2017; Yao and Wu, 2017; Xu et al., 2019; Yao et al.,2020).
However, RWI still faces many challenges in practice. As a waveform fitting process, it is very likely to fall into the local minima when the initial model is far from the true one.A common strategy is to reformulate the inverse problem using traveltimebased objective function (Ma and Hale, 2013; Wang et al., 2015).Many recent works have shown that wave equation reflection traveltime inversion (RTI) can robustly recover the background velocity and thus allow the RWI starting from a better initial model(Brossier et al.,2015;Wang et al.,2018).The information content of the traveltimes and amplitudes are complementary,being sensitive to different features of the model(Wang and Pratt,1997).Therefore,it is necessary to unite RTI and RWI to improve the reconstruction of the low-to-intermediate wavenumber features of the subsurface velocity model,e.g.,Xu et al.(2019).Besides,all the aforementioned RTI and RWI approaches possess the issue of slow convergence because they only use the gradient-based first-order optimization methods.The second-order derivative of the objective function,i.e.the Hessian, implies the information of acquisition geometry,parameter trade-offs and the resolution ability of the observed data(Pratt et al.,1998; Operto et al., 2013; Pan et al., 2016; Wang and Cheng, 2017); therefore, it is a key point to improve the convergence of RWI.In the context of FWI,people use the diagonal or band diagonal Hessian to compensate the spherical divergence/geometric spreading and mitigate parameter trade-offs (Innanen,2014; Shin et al., 2001; Wang et al., 2016). With full or approximate Hessian matrix,the quasi-Newton,Gauss-Newton or Newton method leads to better convergence (Brossier et al., 2009 Metivier et al. 2014, 2017; Liu et al., 2015; Pan et al., 2017). However, the studies of Hessian-based reflection tomography or waveform inversion are very insufficient. Recently, Wang et al. (2020) introduced the Hessian-based Gauss-Newton method to solve the RWI problem in acoustic media.Their attempt shows promising results for the reconstruction of the deep part velocity model.
In this paper,we will propose a practical workflow by cascading Hessian-based RTI and RWI, and provide some computational strategies to support large-scale applications. This paper is organized as follows: First, we will briefly review the Fr′echet derivatives, functional gradient and Hessian matrix for reflectionbased inversion based on the Born approximation. Then, we will introduce some practical strategies to precondition the Hessianbased inversion and deal with the computational challenges. Afterwards, we will demonstrate the two-stage Gauss-Newton RTI/RWI workflow with a real dataset from East China Sea. Finally, we draw some conclusions.
2. Reflection-based wave equation inversion
In the subsurface medium, the traveltime and waveform of seismic waves relate differently to the velocity perturbations. To better understand the reflection-based inverse problems, we first describe the forward problem in the framework of first-order Born approximation, and then review the Fr′echet derivatives of reflection waveform and reflection traveltime.Accordingly,we derive the corresponding functional gradient and approximate Hessian matrices for RWI and RTI, which will be involved in the secondorder optimization methods.
2.1. The reflection waveform sensitivity kernel
The constant-density acoustic wave equation in frequency domain can be written as:

For the RTI and RWI problems, we hope to create the linear relation between the background velocity and reflection wavefield perturbations.Taking the partial derivative of Ψ with respect to v0and making some rearrangements, we have the Fr′echet derivative of reflection data:
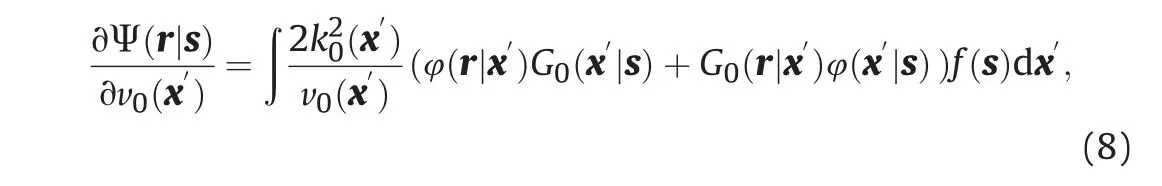
which explains the sensitivity of the reflection data to the change of the background model located at x′. Note that, on the right-hand side of equation (8), there two terms in the bracket of the integration,representing the different branches of the reflection wavepaths. As shown in Fig. 1a, the first term denotes the wavefield emitting from the source is first disturbed by a background velocity perturbation, and then reflected by the reflector. The second term denotes the wavefield is first reflected by the reflectivity and then disturbed by the background velocity perturbation (Fig. 1b). For abbreviation, we define the waveform Fr′echet kernel as:

2.2. The reflection traveltime sensitivity kernel
It is well known that the traveltime is more linearly related to the background velocity structure than waveform. Usually, the traveltime misfit is estimated by the cross-correlation between the observed and synthetic data:



In this way, we can link the traveltime perturbation to the background velocity perturbations. For a given time window, the time integration in equation (11) or (12) is included during the cross-correlation.Accordingly,the frequency bands of the data will not affect the size of Fr′echet derivative because of the crosscorrelation. Thus, the size of Jtwill be greatly reduced by folding the time or frequency axis, which allows the explicit storage of traveltime Fr′echet derivatives if the number of time window is small.
2.3. The inverse problems solved with second-order optimization
The reflection-based inversion aims to retrieve the subsurface model through minimizing the misfit between the observed and simulated reflection data. For instance, RWI updates the background model by solving the following nonlinear optimization problem in a least-squares manner:

where (δv0)krepresents the model update direction, and αkis a step-length that can be computed through a line-search procedure.
The first-order derivative of the objective function (i.e., the gradient) can be expressed as:
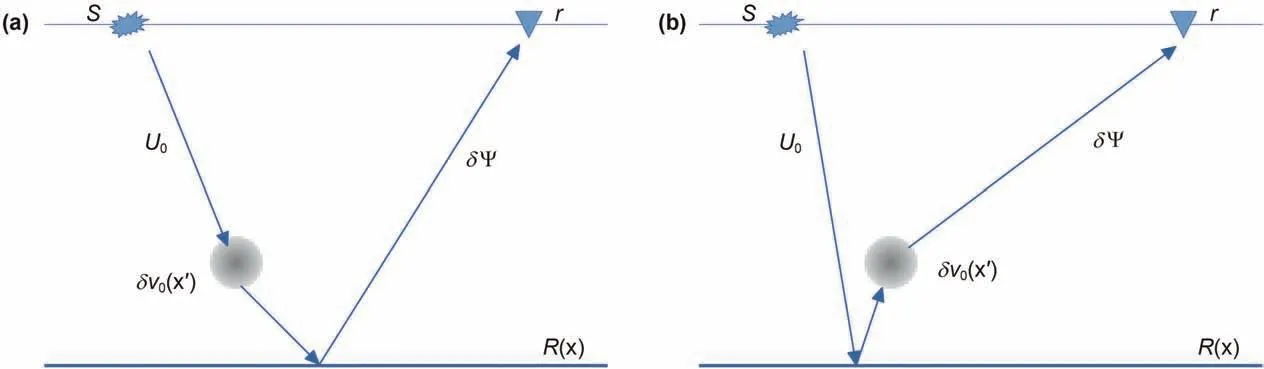
Fig.1. The schematic illustration of two reflection branches: (a) s→δv0(x′)→R(x)→r, (b).s→R(x)→δv0(x′)→r


In the context of RTI, we build the objective function with reflection traveltime difference, namely:

where T denotes the transpose. The widely used first-order optimization methods, such as the steep-descent and nonlinear CG methods, only involves the calculation of the gradient. In the context of RWI or RTI,this can be efficiently implemented by using the adjoint-state method(e.g.,Xu et al.,2012;Ma and Hale,2013).Taking into account the second-order derivative of the objective function(namely the Hessian)and only keeping the linear term,we have the Gauss-Newton equation for RWI and RTI:

At each nonlinear RWI or RTI iteration,either the second-order adjoint-state method or the improved scattering-integral method is used to solve the linear system 18, as in the context of Gauss-Newton FWI (Clement et al., 2001; Plessix, 2006; Metivier et al.,2014; Liu et al., 2015; Pan et al., 2016). These matrix-free CG methods avoid to explicitly form the Hessian matrix and only the Hessian-vector product is required at each iteration of the CG algorithm. The readers are referred to literature, e.g., Metivier et al.(2014); Liu et al. (2015), for the technical details.
3. Practical strategy for large-scale applications
The application of the second-order optimization method to large-scale RTI or RWI problem faces great challenges. First, the inversion generally requires careful preconditioning to get a reasonable model update due to the ill-posedness of this kind of inverse problem. Second, extensive computational resources are required even for a 2-D real data case. The appropriate strategies,such as the decimation in the data or model domain, have to be taken into consideration to make the Gauss-Newton method feasible for the real data applications, although it may sometimes sacrifice the accuracy. Here, we will design some appropriate preconditioning and computational strategies to balance the accuracy and efficiency for the reflection-based inversion.
3.1. Precondition the Hessian matrix
In a layered medium with many interfaces at different depths,the Hessian matrix of RWI may behave very complicated. First, the reflections at different depths and of different offsets experience different geometric spreading during wavefield propagation.Second,the magnitudes of the reflectivity in Born modeling significantly affects the synthetic reflection amplitudes. Therefore, the magnitudes of the Fr′echet kernels for different reflection events could varies in a very wide range. As a result, the elements of Hessian matrix corresponding to the deep locations generally have very small magnitudes.To illustrate this,we use a toy model with two reflectors for the RWI Hessian calculation,which is shown in Fig.2.
We observe that the elements for the first layer are much larger than those of the second layer in the RWI Hessian matrix(Fig.2b).This kind of imbalance increases the ill-conditioning and may lead to unreasonable model updating in the deeper part,since the very small values in the Hessian matrix are truncated during the inner iterations of the Gauss-Newton method. As M′etivier et al. (2017)discussed in the context of FWI, the truncated Gauss-Newton method will benefit from introducing an appropriate preconditioner for the inner linear system.Here we choose to precondition the Hessian in the presence of many interfaces through normalizing the forward modeled data as well as the reflectivity to balance the Fr′echet derivative wavefields at different depths(see Fig.2c).In the numerical examples, we find that this preconditioning improves the Gauss-Newton RTI and RWI algorithms, although it may sometimes sacrifice the resolving power a little bit.
3.2. The computational optimization



Fig. 2. Precondition the RWI Hessian: (a) the modified toy model with two interfaces of the same reflectivity at the depth of 1.8 km and 2.3 km; (b) the original and (c) preconditioned Hessian matrices.


Fig. 3. Schematic illustration of the computational strategies. The Fr′echet kernel will be stored in the coarse grid (Dx× Dz), while the forward modeling is applied on the fine grid (dx × dz). In the meantime, the neighboring receivers will share one Frechet kernel to save the computational and storage overburden.
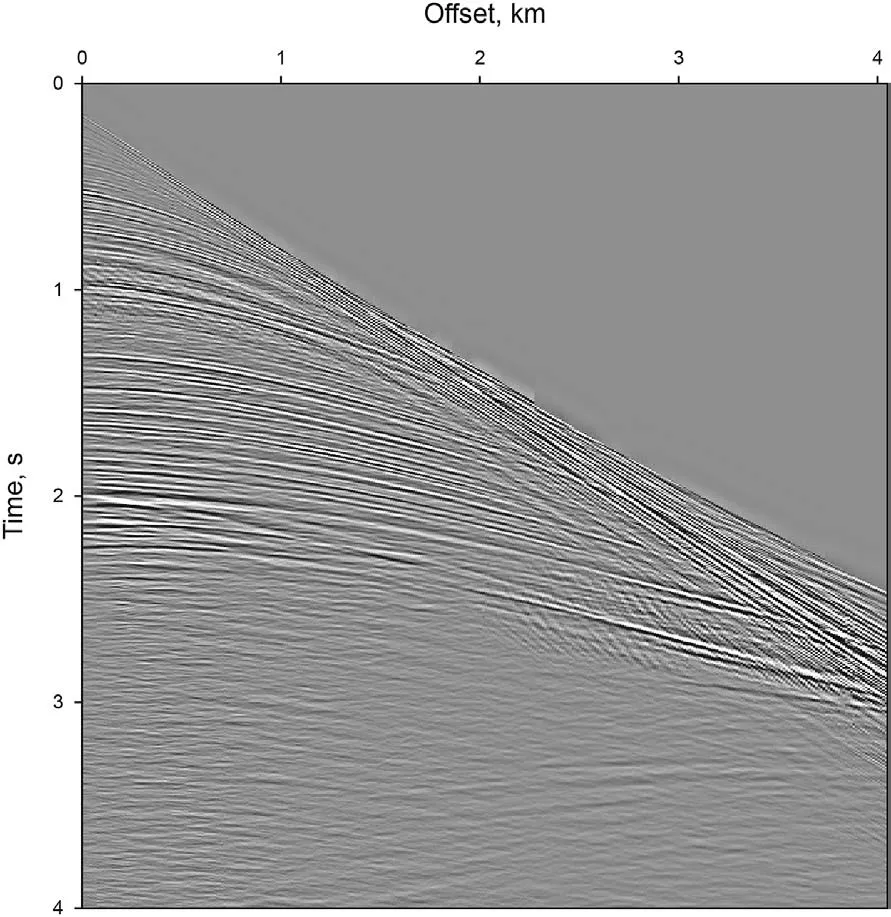
Fig. 4. One common-shot gather of the East China Sea dataset.
4. Field data example
Based on the above strategies,we propose a practical two-stage workflow of reflection-based inversion using the Gauss-Newton method to reconstruct the velocity model. First, we apply Gauss-Newton RTI to reconstruct the low-wavenumber parts of the velocity structures.Then,Gauss-Newton RWI is followed to gradually supplement more intermediate wavenumbers to the model. We test the proposed workflow with a real data from East China Sea.
The 2D dataset of 851 shots was acquired by using air guns and towed streamers in East China Sea.The shot interval is 37.5 m.The spacing of the hydrophones is 12.5 m and the maximum offset is 4 km. Fig. 4 displays one common-shot profile. Conventional data processing, including noise attenuation, designature, deghost and demultiple, have been applied before the inversion. The legacy model for migration is converted from the time-domain root mean square (RMS) velocity, which roughly represents the background features of the target area. However, it is inadequate to correctly honor the kinematics for RTM to provide well-focused migration image and flatten common-image gathers (CIGs)(see Fig. 5).
We apply the proposed two-stage reflection-based inversion to improve the velocity model. The hierarchical strategy with frequency continuation is implemented for both GN-RTI and GN-RWI.In the RTI stage, the resolution of traveltime estimation will be greatly affected by the frequency bands.Therefore,we select three frequency bands, namely 4-8 Hz, 4-12 Hz and 4-16 Hz, to gradually increase the resolution of traveltime estimation along with adaptively designed sliding windows.While in the RWI stage,three frequency groups, 4-8 Hz, 8-12 Hz and 8-16 Hz with an increment of 1 Hz for each group,are used for inversion.For both RTI and RWI, we set 10 outer loops with a maximum 5 iterations in the inner loop for each frequency groups. In the inner loop of Gauss-Newton algorithm, we precondition the Hessian to guarantee a robust convergence of inversion. For comparison,we also perform the conventional workflow based on RTI and RWI with CG method(i.e.,CG-RTI and CG-RWI)to show the effectiveness of the proposed Gauss-Newton algorithm. In addition, the structure-oriented regularization (Yu et al., 2020) are utilized in the aforementioned inversion process to make velocity update geologically consistent.

Fig. 5. Migration results with initial model: (a) the initial velocity model, (b) RTM image and (c) Offset-domain CIGs.
First,we apply the conventional workflow based on CG-RTI and CG-RWI, whose results are shown in Fig. 6. We observe that the velocity update from CG-RTI mainly relates to the strong interfaces,which is not able to flat the CIGs. Starting from CG-RTI model, the velocity is improved after the CG-RWI and thus CIGs are significantly flattened.However,we still observe some residual moveouts on the CIGs,which implies that although the conventional RTI and RWI can provide reasonable migration velocity model,the accuracy of velocity still remains to be improved.For comparison,we use the proposed Gauss-Newton based workflow to update the velocity.After the Gauss-Newton RTI, the velocity is obviously updated for both the shallow and the deep parts (Fig. 7c). The basement imaging of the sedimentary basin is greatly improved with better continuity. The deep faults at the position of 20 km becomes clearer. However, since the multi-window cross-correlation may fail to accurately measure the relatively small traveltime residuals in the latter iterations of this stage, there are still some highwavenumber image footprints on the velocity and the CIGs also exhibit some residual moveouts.Then,starting from the RTI model,we apply the Gauss-Newton RWI, which is sensitive to the waveform misfit, to further improve the recovery of intermediate wavenumbers of the velocity model.As shown in Fig.7b, after the GN-RWI,the velocity anomaly along the strong reflection interface disappears. Some adjustments of velocity model can be observed below the depth of 1.5 km (Fig. 7d), which essentially honors the correct kinematics to flatten the CIGs. The final migrated image based on GN-RWI model shows more continuous sequence boundaries and clear stratigraphic textures.
5. Discussion
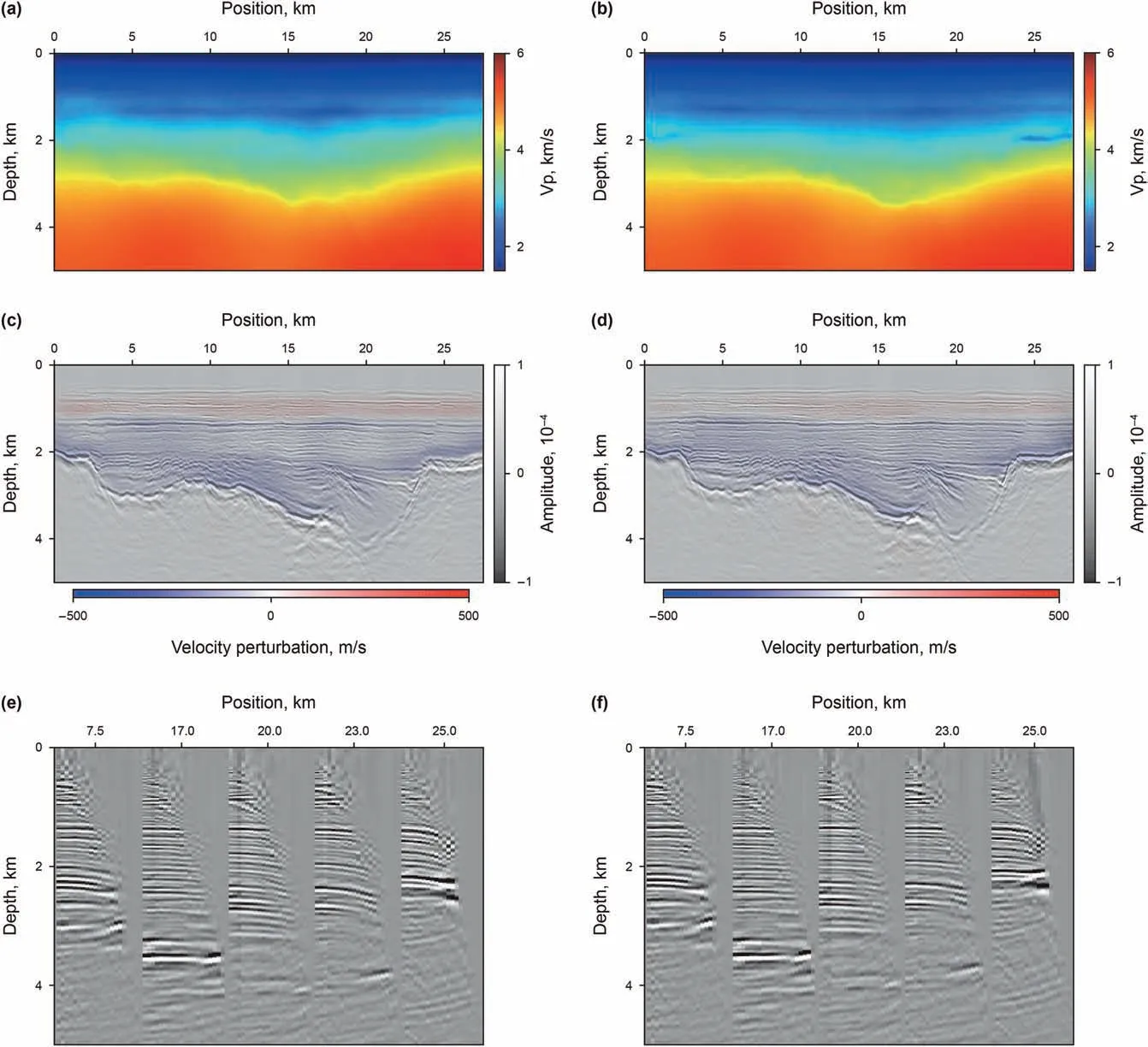
Fig.6. The results from conventional workflow with CG-RTI and CG-RWI.(a)and(b):the CG-RTI and CG-RWI velocity model.(c)and(d):the RTM image using(a)and(b)overlaid by the total velocity update. (e) and (f): the offset-domain CIGs using (a) and (b).
In the stage of RTI, the cross-correlation only estimate the traveltime residuals of the dominant event inside the selected time window. In the presence of multi-events with various intensities,the cross-correlation associated with running windows may fail to provide high-resolution measurement of the traveltime misfits.Other methods, such as dynamic image warping (Hale, 2013),frequency-dependent traveltime measurement(Laske and Masters,1996), and instantaneous phase (Bozdag et al., 2011; Choi et al.,2013) and so on, all have their own disadvantages in this situation. This means that the reflection traveltime or phase inversion has limitation in spatial resolution. That is why the waveform inversion is followed to recover the model intermediatewavenumbers. However, waveform fitting highly depends on the accuracy of the estimated reflectivity(or high-wavenumber model perturbations)and seismic wave propagation physics.According to the radiation pattern, e.g., Wang and Cheng (2017), the density perturbation has a remarkable coupling effect with the P-wave velocity perturbation at small scattering angles. This implies that the effect of density needs to be taken into account in estimation of the high-wavenumber model perturbations to improve the amplitude accuracy of the simulated reflection data. For instance,least-squares RTM based on the variable-density acoustic wave propagator(Yang et al., 2016) could be used for this purpose.
The adjoint-state method plays an important role in the seismic waveform tomography,through which the functional gradient can be efficiently calculated by cross-correlating the forward propagated wavefields with the back-propagated adjoint wavefields(Plessix, 2006; Virieux and Operto, 2009; Fichtner and Trampert,2011). In the context of FWI, both the first- and second-order adjoint-state method are closely related to the scattering-integral method (Tromp et al., 2005; Chen et al., 2007; Epanomeritakis et al., 2008; Liu et al., 2015), but which one is better relies on the acquisition geometry, particularly on the ratio of sources to receivers, as well as the trade-offs between computing cost and file input/output operations (Chen et al., 2007). In this paper, we employ the scattering-integral to calculate the Hessian-vector product in the nested inner loops of Gauss-Newton RWI or RTI.However, for the modern marine and land acquisition system in seismic exploration, the number of receivers is far more than the number of sources,which means that the calculation and storage of Fr′echet derivatives will be extremely resource-demanding without proper computational strategies as aforementioned in the previous sections. Therefore, the second-order adjoint-state method for Gauss-Newton RWI or RTI,which can calculate the Hessian-vector product without explicitly storing the Fr′echet derivatives(Fichtner and Tramper, 2011; Metivier et al., 2017), will be an appropriate alternative in the real data applications (Wang et al., 2021).

Fig.7. The results from proposed workflow with GN-RTI and GN-RWI.(a)and(b):the GN-RTI and GN-RWI velocity model.(c)and(d):the RTM image using(a)and(b)overlaid by the total velocity update. (e) and (f): the offset-domain CIGs using (a) and (b).
6. Conclusions
To improve velocity model building using precritical seismic reflection data, we have reviewed the reflection waveform and traveltime Fr′echet derivatives, and demonstrated Hessian-based second-order optimization methods in the context of RWI and RTI.Accordingly,we have proposed a practical workflow cascading Gauss-Newton RTI and Gauss-Newton RWI, in which Hessian preconditioning and computational strategies, such as coarse grid sampling, receiver decimation and frequency grouping are suggested to make the workflow robust and efficient. The application to a towed-streamer data set with limited offsets has demonstrated that the two-stage workflow is qualified to improve the velocity model and structural imaging in the deep part of the sedimentary basin.
Acknowledgements
This work is supported by National Natural Science Foundation of China (42074157), the National Key Research and Development Program of China (2018YFC0310104) and the Strategic Priority Research Program of the Chinese Academy of Science(XDA14010203).
- Petroleum Science的其它文章
- Primary logistics planning of oil products under the imbalance of supply and demand
- Advances in enhanced oil recovery technologies for low permeability reservoirs
- A novel method of quantitative evaluation and comprehensive classification of low permeability-tight oil reservoirs: A case study of Jidong Oilfield, China
- Measurement of pore diffusion factor of porous solid materials
- Catalytic oxidation of pentanethiol on basic nitrogen doped carbon hollow spheres derived from waste tires
- Temperature effect on the dynamic adsorption of anionic surfactants and alkalis to silica surfaces

