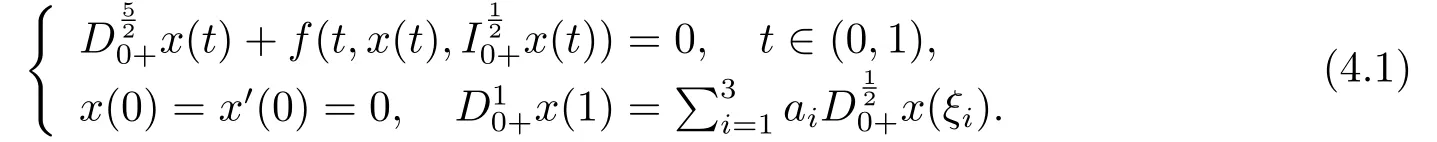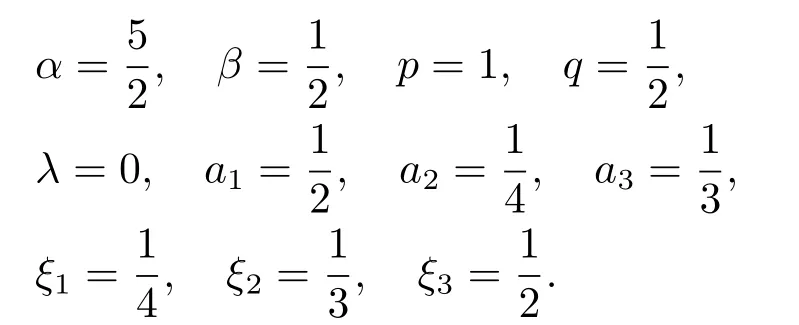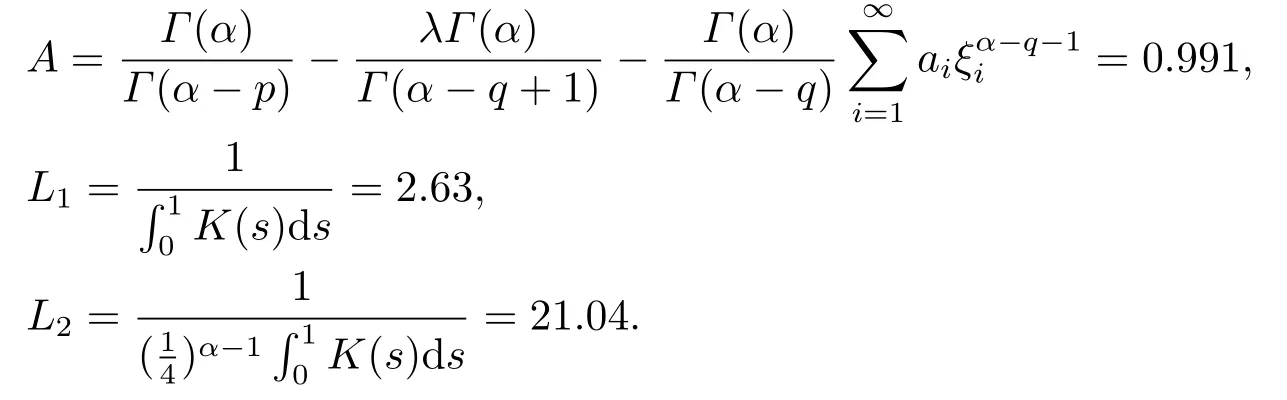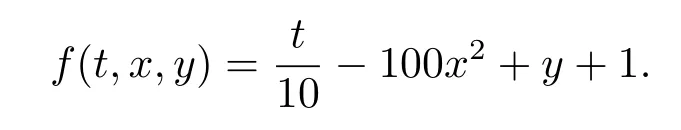Existence of Positive Solutions for a Fractional Differential Equation with Multi-point Boundary Value Problems
DONG Weiping(董偉萍), ZHOU Zongfu(周宗福)
(School of Mathematical Sciences, Anhui University, Hefei 230601, China)
Abstract: In this article, we study multi-point boundary value problems of a class of fractional differential equation.By means of the Guo-Krasnoselskii fixed point theorem and Leggett-Williams fixed point theorem, some existence and multiplicity results on the positive solutions are acquired.A simple example is given to show the application of the main results.
Key words: Positive solution; Fractional differential equation; Existence and multiplicity; Multi-point
1.Introduction
Fractional calculus is a theory about differential and integral of any order.It is an extension of integral calculus.In real life, fractional differential equations are often used to describe new materials, chemical processes, control theory, biological stochastic models and other application fields.Therefore, a growing number of people study and pay attention to fractional calculus.[1?3]
In the past several decades,the research of various fractional order boundary value problems makes its application in many fields more significant.In [4-8], the authors studied existence of solutions for fractional boundary value problems.Recently, under the complex boundary conditions, the research on the existence and uniqueness of the positive solutions of fractional differential equations has attracted more and more scholars’ attention.These studies are based on a series of fixed point theorems, such as: Banach’s contraction mapping principle, Krasnoselskii’s fixed point theorem, the Guo-Krasnoselskii fixed point theorem and the Leggett-Williams fixed point theorem, etc.[9?12]
In [4], LI and LUO considered the following nonlinear fractional BVP
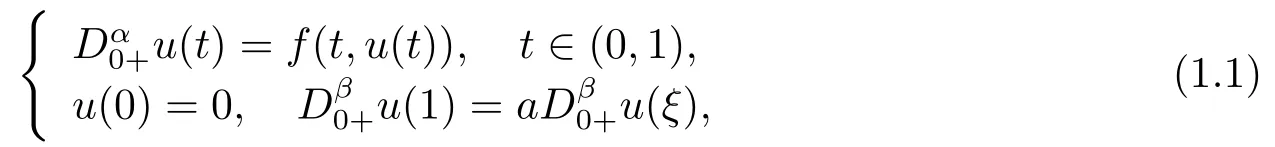
where 1< α ≤2, 0≤β ≤1, 0< ξ <1, 0≤a ≤1, withaξα?β?2<1?β, 0≤α ?β ?1.By means of Guo-Krasnoselskii fixed point theorem and Nonlinear alternative, the existence of positive solutions for BVP (1.1) was showed.
Recently, in [11], JIANG and WANG studied the existence and uniqueness result for multi-point boundary value problem given by
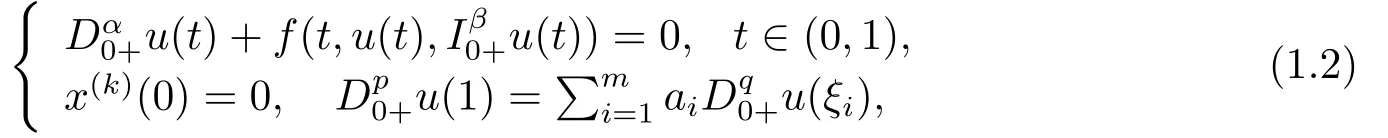
wherek= 0,1,···,n ?2,n ?1< α ≤n,n ≥2, 0< β <1,p ∈[1,n ?2],q ∈[0,p],0< ξ1< ξ2< ··· < ξm <1,ai >0 (i= 1,2,···,m),f ∈C([0,1]×R2,R).Using Banach’s contraction mapping principle, Krasnoselskii’s fixed point theorem, the Nonlinear alternative and Boyd and Wong fixed point theorem, some existence and uniqueness results of solutions are obtained.
Enlightened by the above literature, we discuss the following fractional boundary value problem
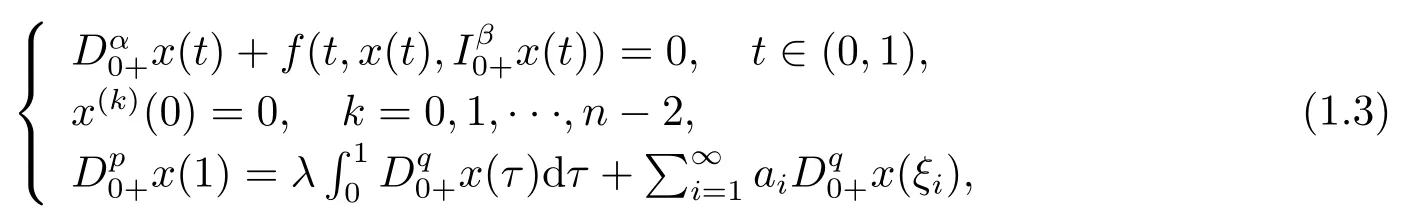

In BVP (1.3),q ∈[0,p].This implies thatqcan be not equal top.In this situation,the construction of Green’s function becomes more complex, and enlarging and shrinking the Green’s function requires more techniques.In addition, by using the Leggett-Williams fixed point theorem, we can obtain the existence of at least three positive solutions for BVP (1.3),which is more significant and applicable.
The rest of this article is organized as follows: In Sec.2, we present some important preliminaries and lemmas.In Sec.3, the existence and multiplicity results are established based on the fixed point theorems.In Sec.4, an example is presented to support our main results.
2.Preliminaries
Definition 2.1[1]Letf:(0,+∞)→R is a continuous function, the Riemann-Liouville fractional derivative of orderα(α>0) offis defined as following
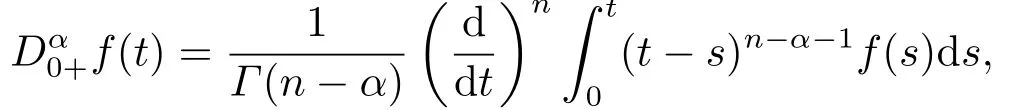
wheren=[α]+1, provided that the right-hand side is pointwise defined on (0,+∞).
Definition 2.2[1]Letf:(0,+∞)→R is a continuous function, the fractional integral of orderα(α>0) offis defined as following
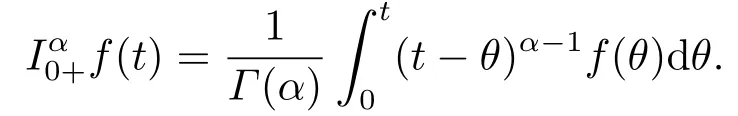
Lemma 2.1[1]Letf ∈L[0,1]∩C[0,1],α>0, then=0 have unique solution of
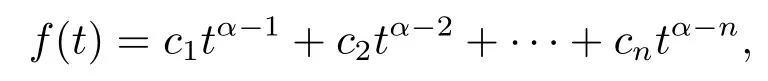
for someci ∈R,i=1,2,··· ,n,nis the smallest integer greater than or equal toα.
Lemma 2.2[1]Letf ∈L[0,1]∩C[0,1],α>0, then
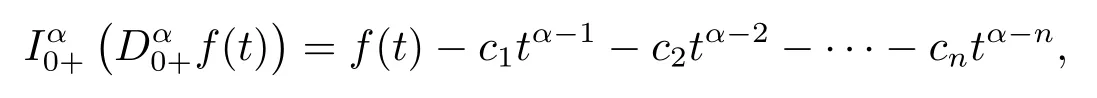
for someci ∈R,i=1,2,··· ,n,nis the smallest integer greater than or equal toα.
Lemma 2.3[2]LetPbe a cone in a real Banach spaceE, Pc={x ∈P:‖x‖ (C1){x ∈P(θ,b,d)|θ(x)>b}?, andθ(Tx)>bforx ∈P(θ,b,d); (C2)‖Tx‖ (C3)θ(Tx)>bforx ∈P(θ,b,c), with‖Tx‖>d. Then T has at least three fixed pointsx1,x2andx3, which satisfy‖x1‖ < a, b < θ(x2) anda<‖x3‖withθ(x3) Lemma 2.4Forh ∈C(0,1)∩L1(0,1),the solution of the linear fractional differential equation supplemented with the boundary conditions is equivalent to the integral equation where ProofFor Lemma 2.2, we have It follows fromx(0)=x′(0)=···=x(n?2)(0)=0 that Thus which, together with the boundary value condition implies that i.e., Then, by (2.3), we get This proof is completed. For the sake of computational convenience, we set Lemma 2.5(2.1) in Lemma 2.4 can be written as where and where A, B are given by (2.2), (2.4) respectively. ProofFor Lemma 2.4, we have This proof is completed. Lemma 2.6The functionsg1andg2given by (2.10) have the properties: (v)g1andg2are continuous on [0,1]×[0,1],g1(t,s)≥0,g2(t,s)≥0, for allt,s ∈[0,1]. Proof(i) From (2.10), we have (ii) From (2.10), we have (iii) From (2.10), we have (iv) From (2.10), we have (v) From the definitions ofg1andg2, we haveg1andg2are continuous on [0,1]×[0,1].Moreover, becauser1(s)≥0,r2(s)≥0, by (iii) and (iv), we haveg1(t,s)≥0,g2(t,s)≥0, for allt,s ∈[0,1]. This proof is completed. Lemma 2.7G(t,s) is continuous on [0,1]×[0,1], and satisfies (i)G(t,s)≤Dtα?1for allt,s ∈[0,1], whereDis given by (2.5); (ii)G(t,s)≥tα?1K(s) for allt,s ∈[0,1], where ProofBy definition of the functionG(t,s),we know that for allt,s ∈[0,1],the functionG(t,s) is continuous. (i) By Lemma 2.6, we obtain for allt,s ∈[0,1], (ii) By Lemma 2.6, we obtain for allt,s ∈[0,1], This proof is completed. LetE=C[0,1], thenEis a Banach space with the norm‖x‖= sup0≤t≤1|x(t)|.LetP={x ∈E:x(t)≥0,t ∈[0,1]}.It is clear thatPis a cone in C[0,1].We define an operatorT:E →Eas follows: Observe that the fixed points of operatorTcoincide with the solution of problem (1.3). Theorem 3.1T:P →Pis completely continuous. ProofT:P →Pis continuous in view of nonnegative and continuity ofG(t,s) andf.Next, we shall show thatTis compact inP.SupposeΩ ?Pis bounded, then,?M >0,?x ∈Ω,s.t.‖x‖≤M.TakeM1=max{f(t,x,y):0≤t ≤1,0≤x ≤M,0≤y ≤From Lemma 2.7,?x ∈Ω, we have SoT(Ω) is uniformly bounded.Moreover, for allt1,t2∈[0,1] witht1 From uniformly continuity ofG(t,s) on [0,1]×[0,1], we have|(Tx)(t2)?(Tx)(t1)|tends to zero independent ofxast2→t1,soT(Ω)is equicontinuous.By the Arzela-Ascoli theorem,T(Ω) is relatively compact.Hence, the operatorTis compact.Consequently,T:P →Pis completely continuous. In the following result, we consider the existence and multiplicity of positive solutions for BVP (1.3). Theorem 3.2Assume that there exists two positive constantsr2>r1>0 such that whereL1,L2are given by (2.6),(2.7) respectively.Then BVP (1.3) has at least one positive solution whenλ=0. ProofLetP1={x ∈E:x(t)≥tα?1‖x‖,?t ∈[0,1]}, it is clear thatP1is a cone inE.From Lemma 4 in [12], we can know that ifλ=0,tα?1K(s)≤G(t,s)≤K(s), and then SoT(P1)?P1.Then, by similar certification through Theorem 3.1, we conclude thatT:P1→P1is completely continuous. LetΩ1={x ∈P1:‖x‖ which means whenx ∈?Ω1,‖Tx‖≥‖x‖. Whenx ∈?Ω2, for anyt ∈[0,1], we haveBy Lemma 2.7 and (H1), we get which means whenx ∈?Ω2,‖Tx‖≤‖x‖. Consequently, by the Guo-Krasnoselskii fixed point theorem,Thas a fixed point inP1∩(Ω2Ω1), which means that BVP (1.3) has at least one positive solution whenλ= 0.The proof is completed. Theorem 3.3Assume that there exist constants 0< a < b < d ≤csuch that the following assumptions hold: whereL2,L3are given by (2.7),(2.8) respectively.Then BVP (1.3) has at least three positive solutionsx1,x2, andx3with ProofDefine a nonnegative continuous concave functionθonPas If={x ∈P:‖x‖≤c}, then‖x‖≤c, andθ(x)≤‖x‖.It follows from (G3) thatf(t,x,y)≤L3c, hence which shows that condition (C2) of Lemma 2.3 is fulfilled. Letx(t)=it is easy to know thatx ∈P(θ,b,d) and{x ∈P(θ,b,d)|θ(x)>b}?.Ifx ∈P(θ,b,d), we haveb ≤x(t)≤dfor anyby (G2), we have So the condition (C1) of Lemma 2.3 holds. Whenx ∈P(θ,b,c) with‖Tx‖>d, by (G2), we have So the condition (C3) of Lemma 2.3 holds. Consequently, by Lemma 2.3,Thas at least three fixed pointsx1,x2andx3inP,which means that BVP (1.3) has at least three positive solutionsx1,x2, andx3with The proof is completed. Example 4.1Let us consider the following differential equation boundary value problem: We take After a simple computation, we have We consider We taker2=1,r1=then we find that Therefore, the conditions of Theorem 3.2 are all satisfied.Thus, by Theorem 3.2, we can conclude that the problem (4.1) exists at least one positive solution.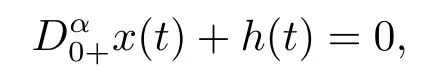
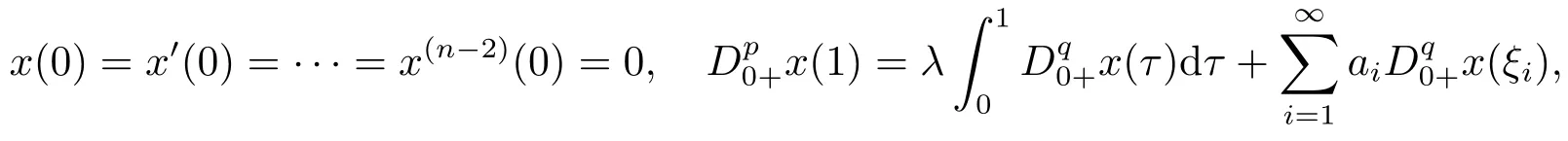
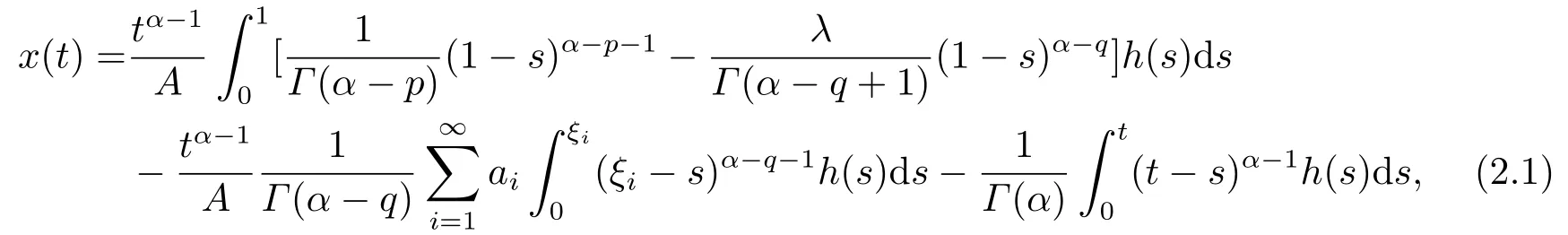
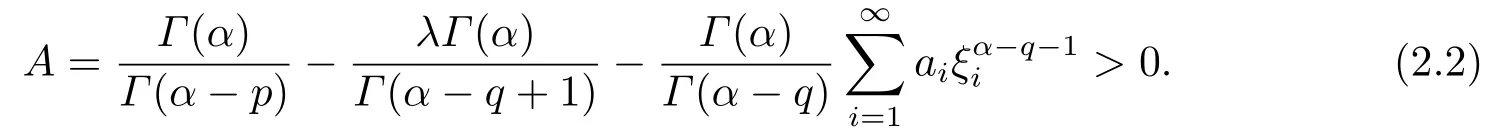

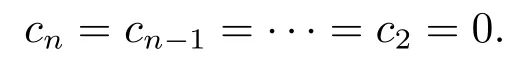
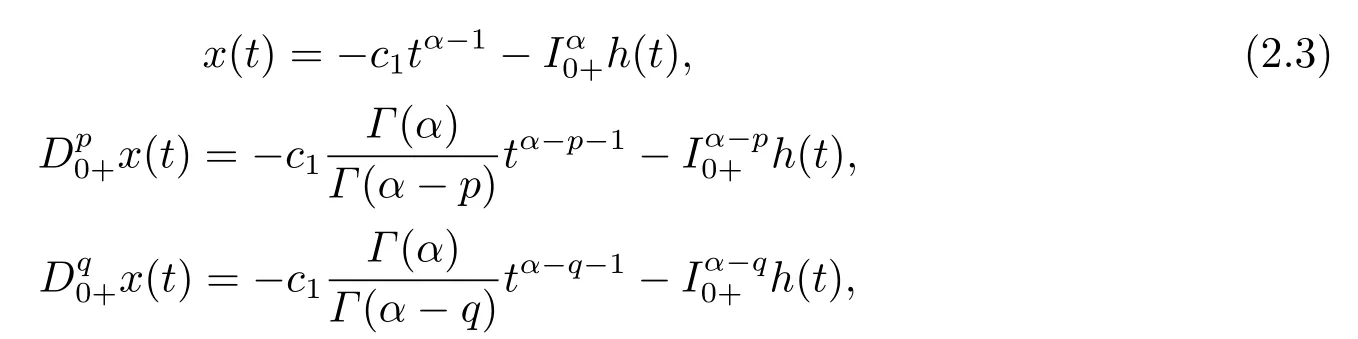
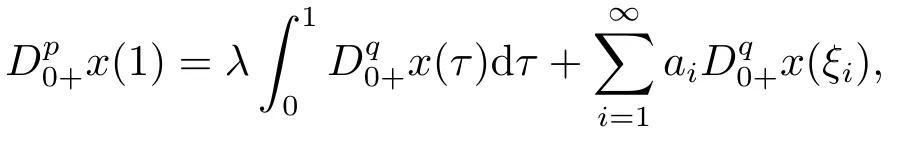





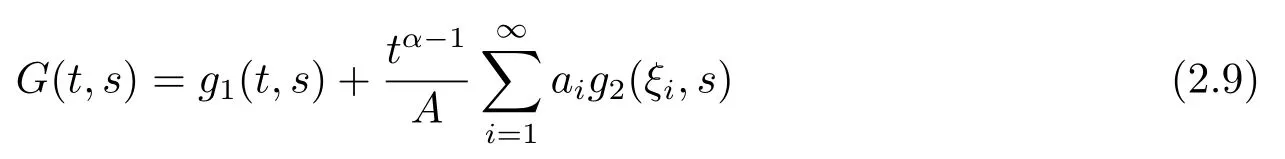
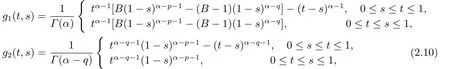

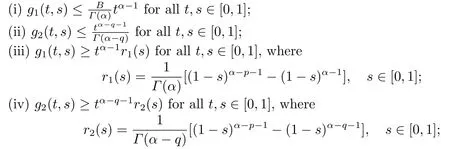
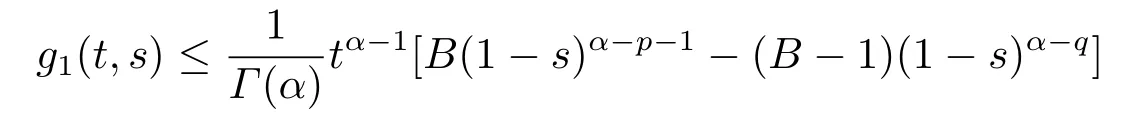
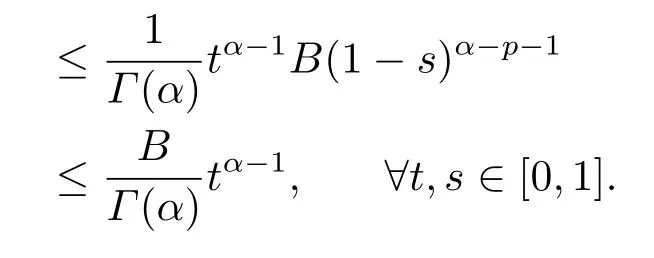
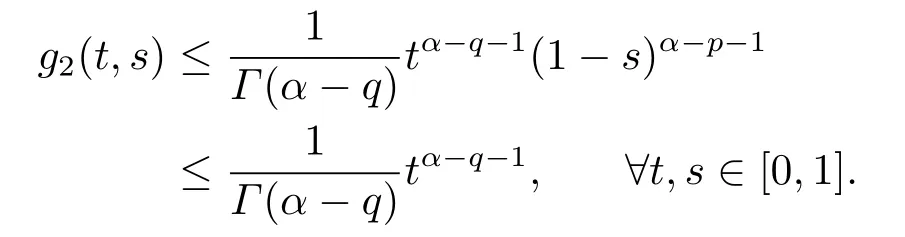
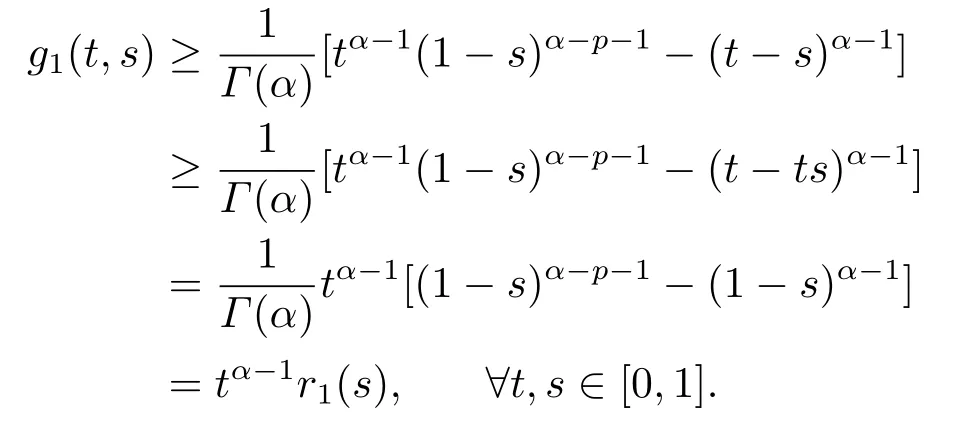
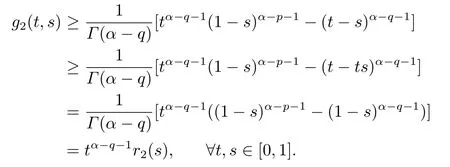

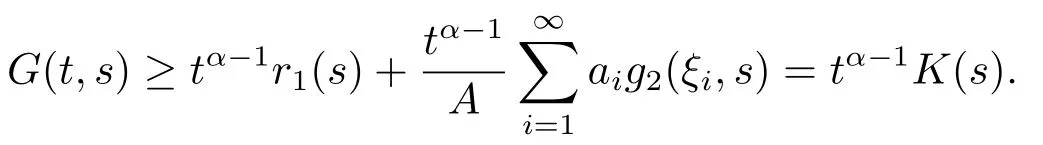
3.Main Results
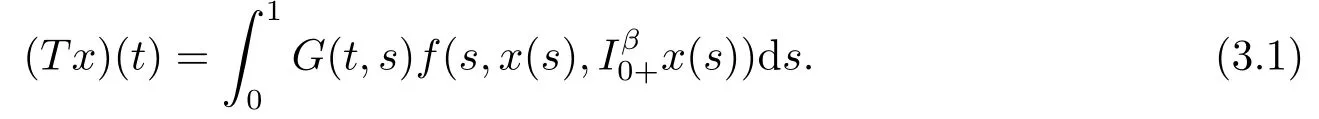
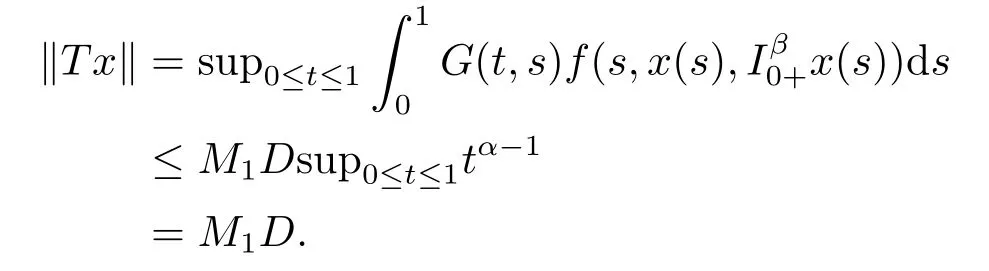

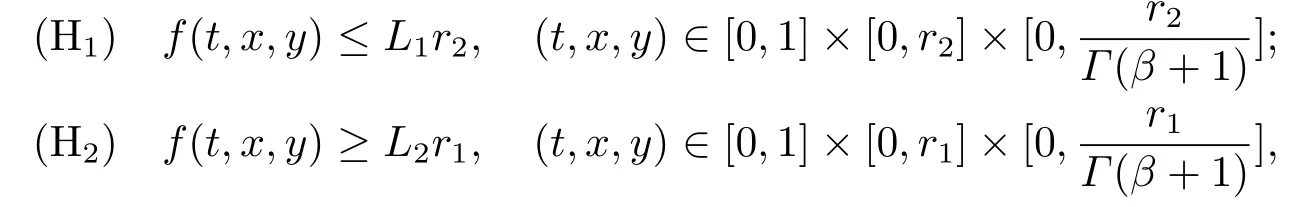

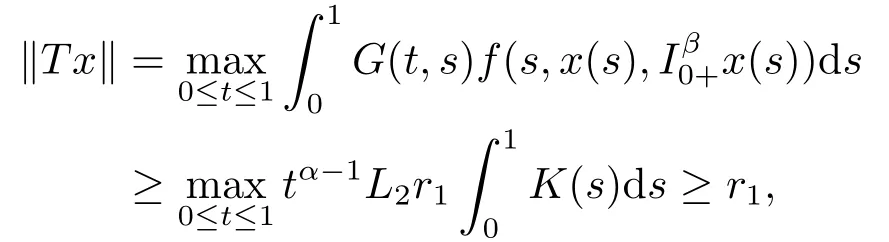
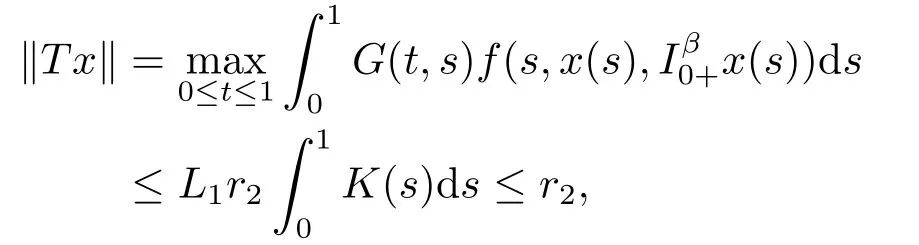
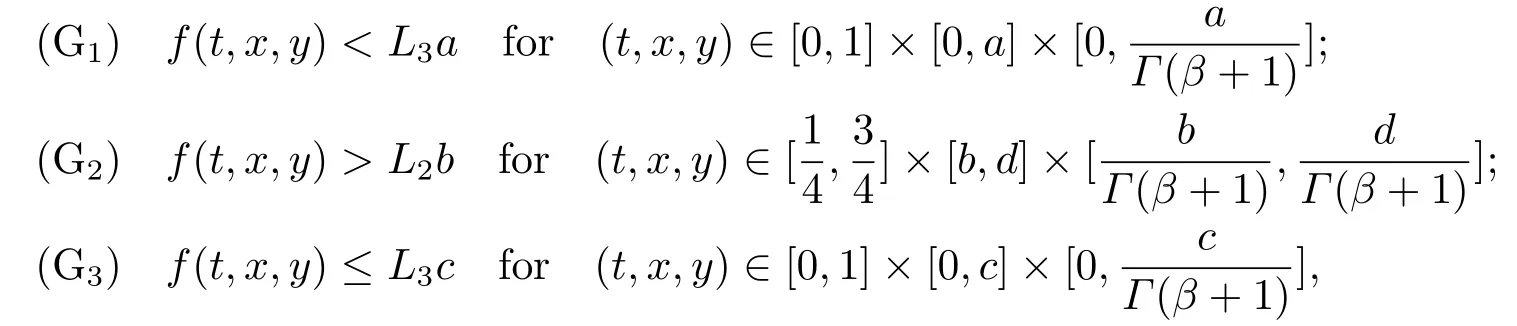
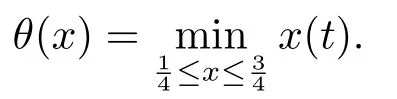
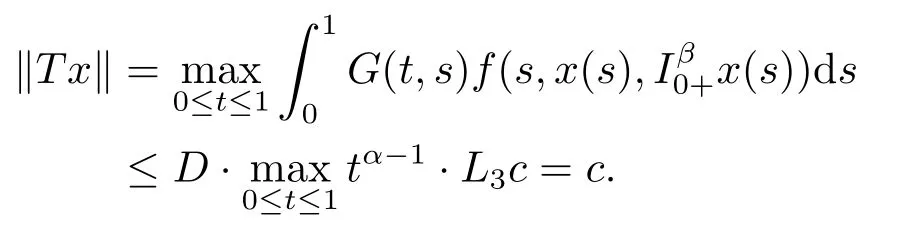
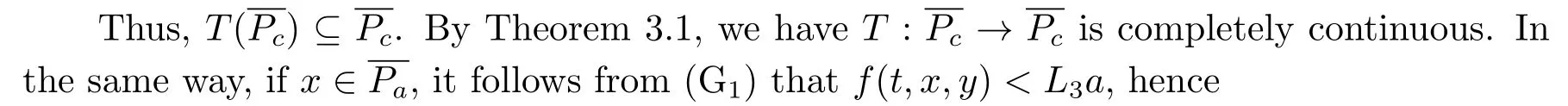
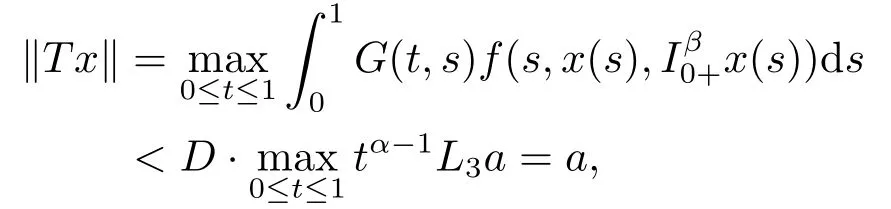
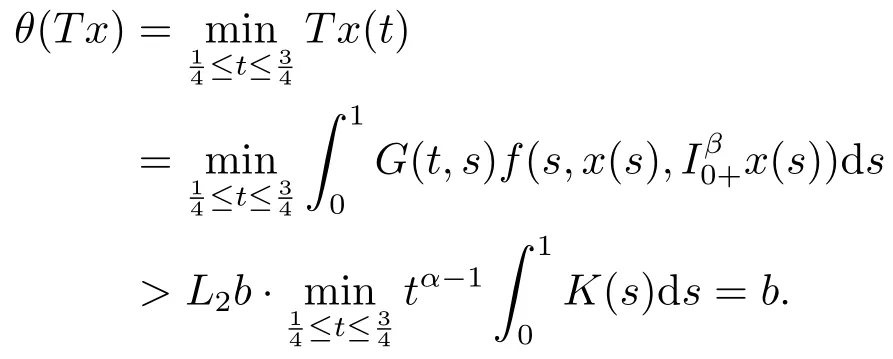

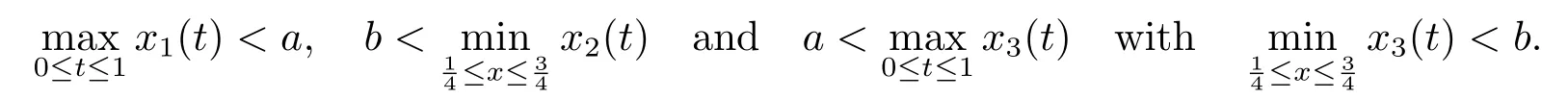
4.Main Results