Solvability of Mixed Fractional Periodic Boundary Value Problem with p(t)-Laplacian Operator

TANG Xiaosong(湯小松), WANG Zhiwei(王志偉)

(School of Mathematics and Physics, Jinggangshan University, Ji’an 343009, China)

Abstract: In this paper, we investigate the mixed fractional periodic boundary value problem with p(t)-Laplacian operator.For making use of the continuation theorem to study the existence of solutions, we rewrite the original mixed fractional periodic boundary value problem as an equivalent system and obtain the existence results of solution under the appropriate conditions of the nonlinear term.The obtained results enriched and generalized the existing literatures.At last, an example is given out to demonstrate the main results.

Key words: Mixed fractional derivative; Periodic boundary value condition; p(t)-Laplacian operator; Existence; Continuation theorem

1.Introduction

Fractional derivative was introduced by Leibnitz in the letter to L’Hospital[1].Fractional calculus is a generalization of ordinary differentiation and integration on an arbitrary order that can be non-integer.However, it was not developed before the 20th century, since it was short of a physical meaning or application.In recent decades,due to the intensive development of the theory of fractional calculus itself[2?3]and its applications[4], more and more scholars have been of great interest in fractional differential equations[5?9].

The mathematical modeling of a variety of physical processes gives rise to a class of periodic boundary value problems, which have recently received considerable attention[10?13].In [11], CHEN and LIU have considered the following periodic boundary value conditions withp-Laplacian operator

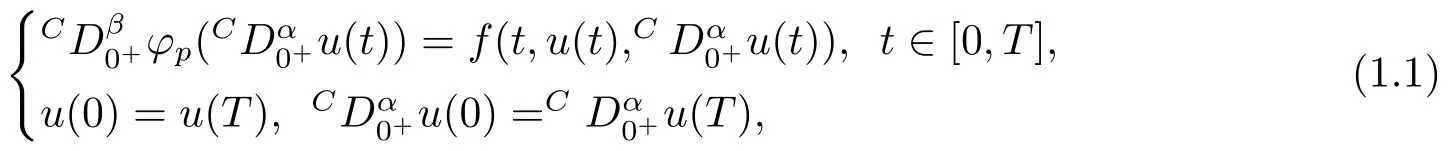
where 0< α,β ≤1, 1< α+β ≤2,Cis a Caputo fractional derivative,φp(·) is ap-Laplacian operator,f:[0,T]×R→R is continuous.They obtained the existence of solutions for (1.1) by using a new continuation theorem.Here, we have to stress that in the above paper,p-Laplacian operator is not relate witht.

In this paper, we shall discussp(t)-Laplacian operator, which is relate witht.Noting that thep(t)-Laplacian operator is the non-standard growth operator which arises from nonlinear electrorheological fluids[14], image restoration[15], elasticity theory[16], etc.This class of problems have recently received considerable attention.[17?19]It’s worth pointing out that the authors[11]investigated the existence of solutions for (1.1) under the Caputo fractional derivative.Then, a question appears naturally in the authors’ mind: “If a Riemann-Liouville fractional derivativein (1.1) is substituted for the Caputo fractional derivativeChow can we find the existence of solutions?”

Driven by the above question,our paper aims to investigate the existence of solutions for the following mixed fractional periodic boundary value problem withp(t)-Laplacian operator

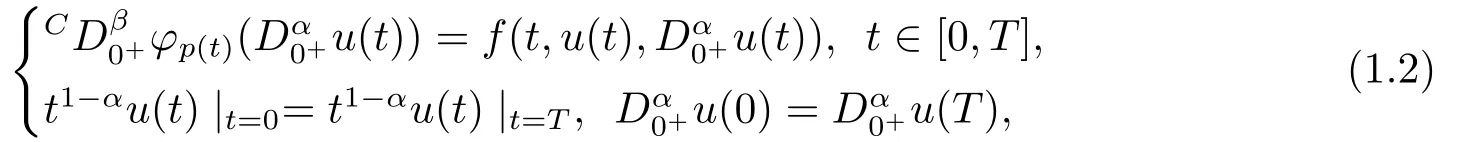
where 0< α,β ≤1, 1< α+β ≤2,Cis a Caputo fractional derivative andis a Riemann-Liouville fractional derivative,φp(t)(·) is ap(t)-Laplacian operator,p(t)>1,p(t)∈C1[0,T] withp(0)=p(T),f:[0,T]×R2→R.For eachh ∈C([0,T],R), we can easily prove that the periodic boundary value problem as follows:

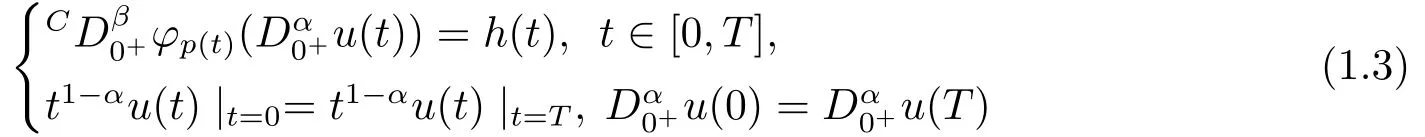
is not solvable.And, even if solvable, PBVP (1.3) has no unique solution becausex(t)+cis a solution together withx(t) for?c ∈R.In this case, we can derive the following condition

for the solvability of PBVP (1.3).Moreover,is a nonlinear operator,which implies that the coincidence degree theory for linear differential operators with periodic boundary value conditions is invalid in the direct application to it.However, if we rewrite(1.2) as the system (2.1), we can make use of the continuation theorem on the problem (1.2)and obtain the existence of solutions for the problem (1.2).

The rest of this paper is organized as follows.In Section 2, we present some auxiliary lemmas later used.In Section 3, the existence results of solutions for (1.2) is established by using the continuation theorem of coincidence degree theory.Finally, an example is given out to illustrate our main results.

2.Preliminary Results

For basic definitions of Caputo fractional derivati ve,Riemann-Liouville fractional derivative and Riemann-Liouville fractional integral, please see [3, 5].Here, we give out and show some important properties and lemmas as follows.

Lemma 2.1[19]For any (t,u)∈[0,T]×R,φp(t)(u) =|u|p(t)?2uis a homeomorphism from R to R and strictly monotone increasing for any fixedt.Moreover, its inverse operatoris defined by

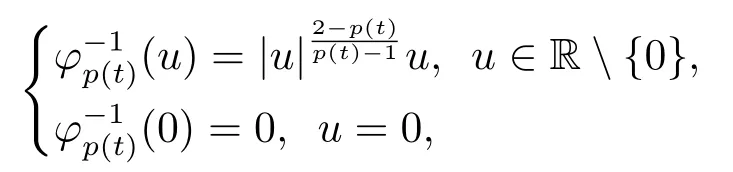
which is continuous and sends bounded sets to bounded sets.

Now, we briefly recall some notation and an abstract existence result due to Mawhin[20].

LetX, Ybe two real Banach spaces andL: domL ?X →Yis a linear operator,N:X →Yis nonlinear continuous map.If dimkerL=dim(Y/ImL)<+∞, and ImLis a closed set ofY, thenLis a Fredholm map of index zero.IfLis a Fredholm map of index zero, andP:X →X,Q:Y →Ybe projectors such that ImP=KerL, KerQ=ImL,X=KerL⊕KerP,Y=ImL⊕ImQ.It follows thatLp=L|domL∩KerP:domL∩KerP →ImLis invertible.We denote the inverse byKp.LetΩis an open bounded subset ofX, and dom, the mapN:X →Ywill be calledL-compact onis bounded andK(I ?Q)N:is compact.

Lemma 2.2[20]LetX, Ybe real Banach spaces,L:domL ?X →Ybe a Fredholm operator of index zero andN:X →YbeL-compact onΩ.Assume that the following conditions are satisfied

1),?(u,λ)∈[(domLKerL)∩?Ω]×(0,1);

2),?u ∈KerL ∩?Ω;

3) deg(JQN,Ω∩KerL,0)0, where,J: ImQ →KerLis an isomorphism map.

Then the equationLu=Nuhas at least one solution in dom

Moreover, we need the following auxiliary lemmas to prove the existence of solutions for the problem(1.2).For using the continuation theorem to investigate the existence of solutions for the problem (1.2), we consider the following system:

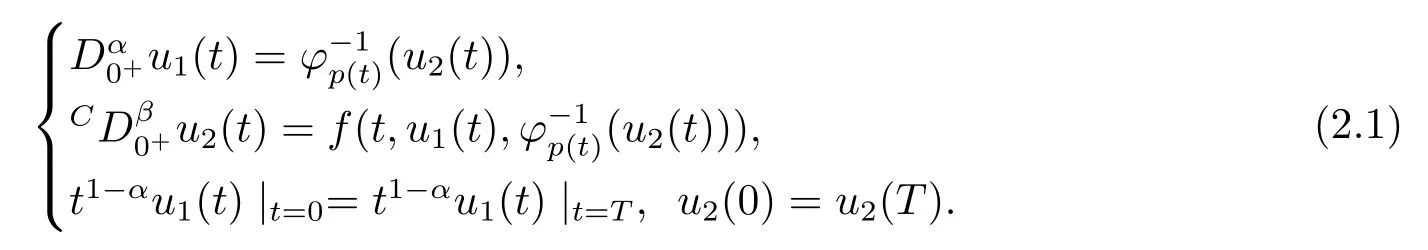
Obviously, we can easily see thatu1(·) must be a solution of problem (1.2) if (u1(·),u2(·))Tis a solution of problem(2.1).Therefore,to prove the problem(1.2)has solutions,it is sufficient to show that problem (2.1) has solutions.

Define the operatorL: domL ?X →Yby

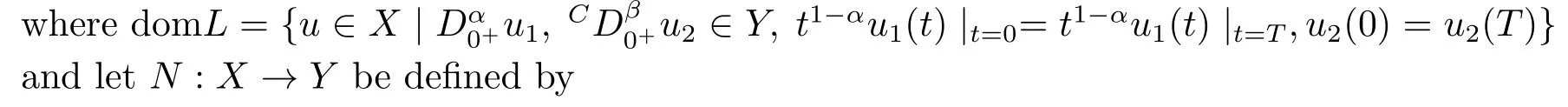
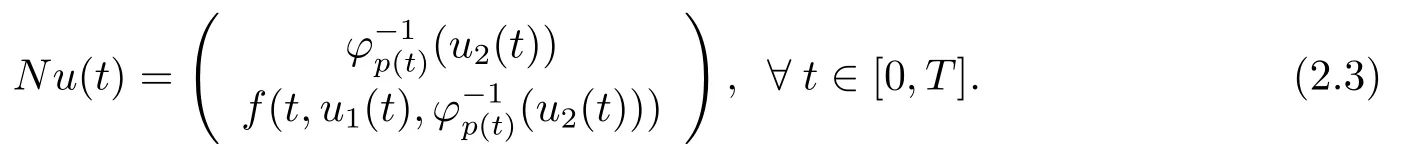
It is easy to see that problem (2.1) can be converted to the operator equation

Lu=Nu, u ∈domL.

Lemma 2.3LetLbe defined by (2.2), then

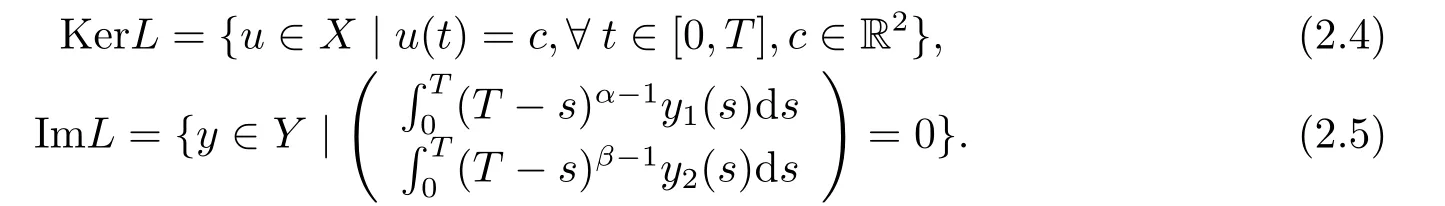
ProofObviously,by the Caputo fractional derivative and Riemann-Liouville fractional integral, we can see that (2.4) holds.

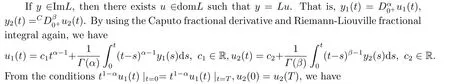
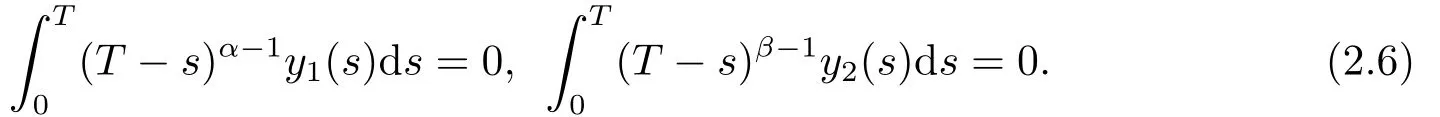
Thus, we get (2.5).

Lemma 2.4LetLbe defined by (2.2), thenLis a Fredholm operator of index zero,and the linear continuous projector operatorsP:X →XandQ:Y →Ycan be defined as

Furthermore, the operatorKP:ImL →domL∩KerPcan be written by

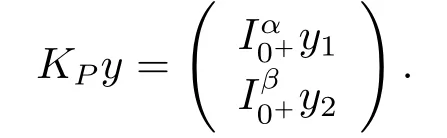
ProofObviously, ImP=KerLandP2u=Pu.It follows fromu=(u ?Pu)+PuthatX=KerP+KerL.By simple calculation, we can get that KerP∩KerL={0}.Then we get

X=KerL ⊕KerP.

For anyy ∈Y, we have

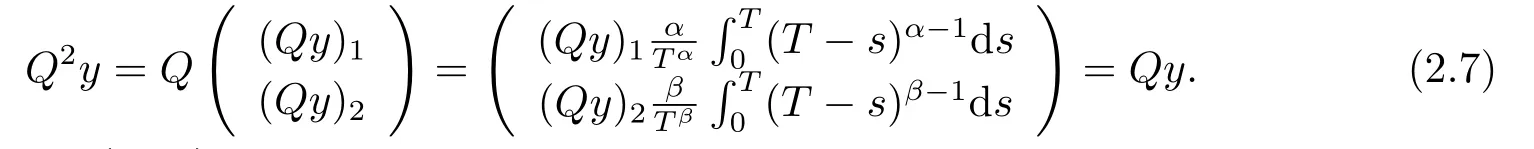
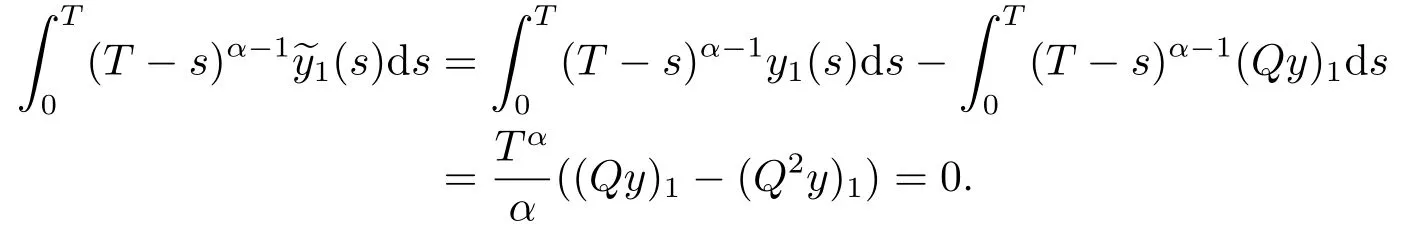
dim KerL=dim ImQ=codimImL=2.

This means thatLis a Fredholm operator of index zero.

From the definition ofKP, fory ∈ImL, we have

On the other hand, foru ∈domL∩KerP, we havet1?αu1(t)|t=0=u2(0)=0.Thus, we get

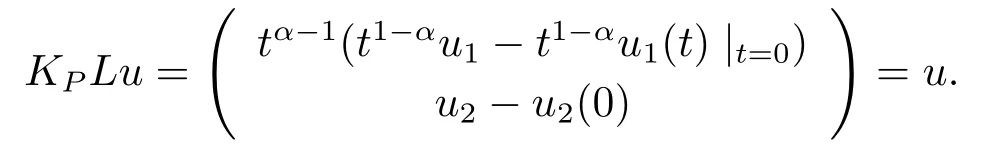
So, we know thatKPis the inverse ofLP.The proof is complete.

3.Main Results and an Example

In this section,we firstly investigate the existence of solutions for mixed fractional periodic boundary value problem withp(t)-Laplacian operator, which is based on the coincidence degree theory.Then, we will give an example to illustrate the validity and practicability of our main results.Furthermore, in order to state the following Theorem 3.1, we denote that

Theorem 3.1Assume that the following condition holds.

(H1) There exist nonnegative functionsa(t),b(t),c(t)∈C[0,T] such that

|f(t,u,v)|≤a(t)+b(t)|u|ν?1+c(t)|v |ν?1,(t,u,v)∈[0,T]×R2,1<ν ≤Pn;

(H2) There exists a constantD >0 such that

uf(t,u,v)>0, ?t ∈[0,T], v ∈R, |u|>D,

or

uf(t,u,v)<0, ?t ∈[0,T], v ∈R, |u|>D.

Then, the problem (1.2) has at least one solution, provided that

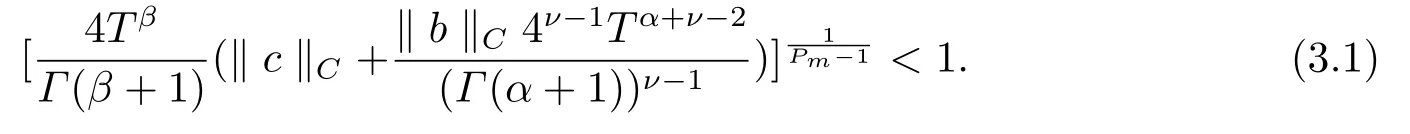
ProofLet

Ω1={u ∈domLKerL|Lu=λNu,λ ∈(0,1)}.

Foru ∈Ω1, we haveNu ∈ImL.So, by (2.5), we obtain

From the integral mean value theorem, there exist constantsξ,η ∈(0,T) such thatu2(ξ)=0 andf(η,u1(η)(u2(η)))=0.So, from the condition (H2), one has|u1(η)|≤D.

By the Riemann fractional derivative and Riemann-Liouville fractional integral, we have

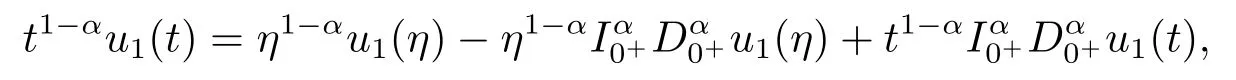
which together with

and|u1(η)|≤Dyields that

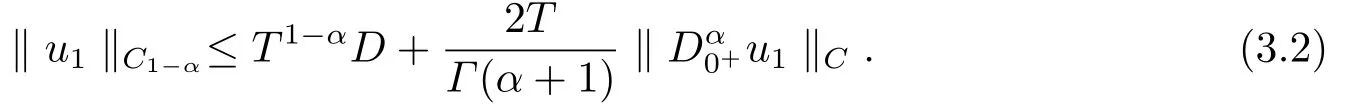
On the other hand, ifu ∈Ω1, we get

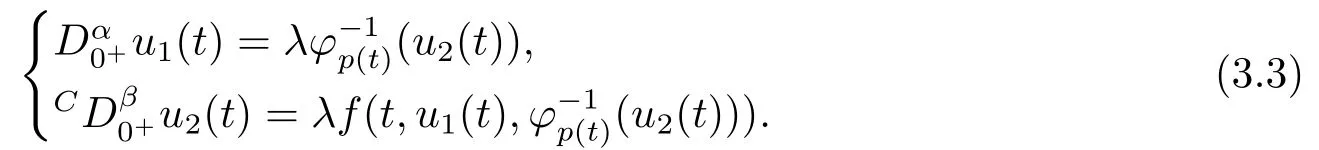
From the first equation of (3.3), we obtainu2(t) =φp(t)(λ?11(t)).By substituting it into the second equation of (3.3), we get

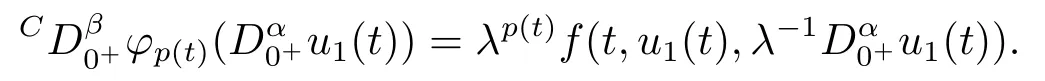
Thus,by the Caputo fractional derivative and Riemann-Liouville fractional integral,we obtain

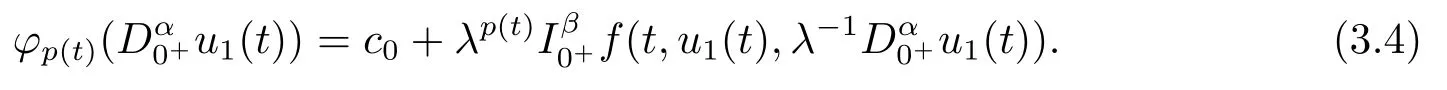
Then we have

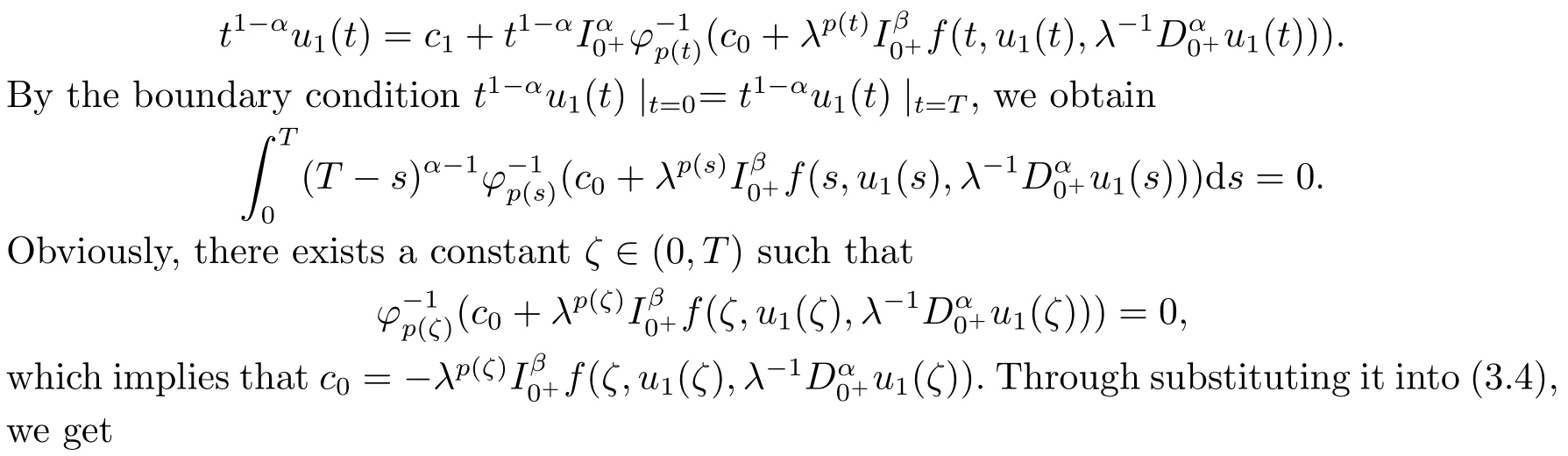
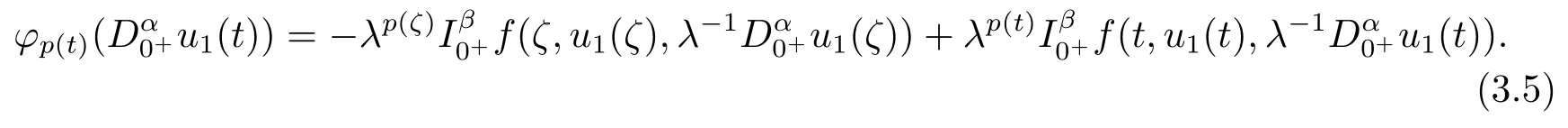
From the condition (H1), we get

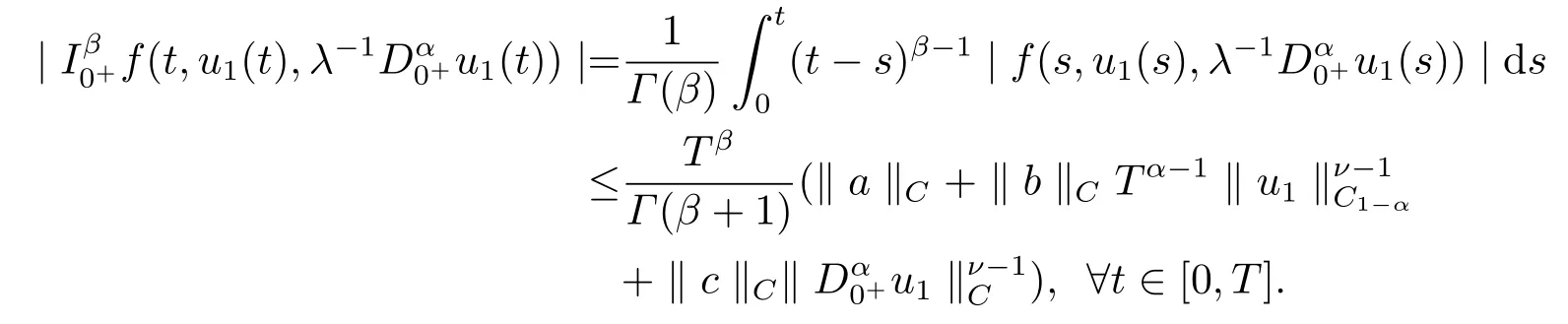
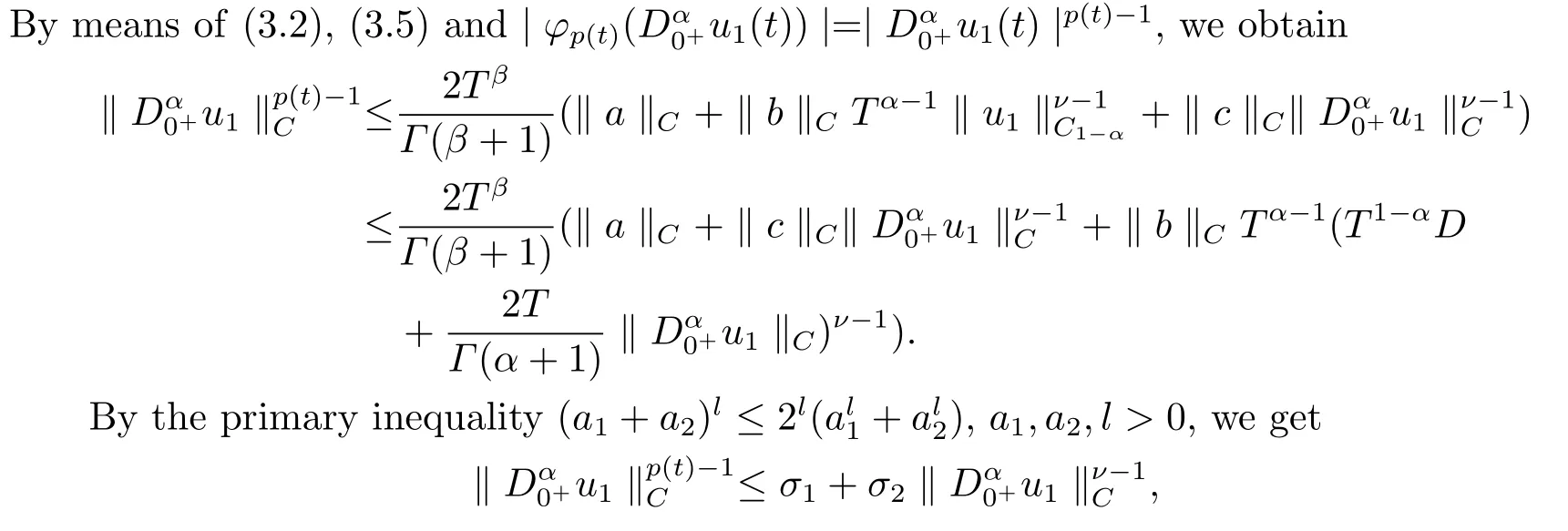
where

Hence, we can obtain

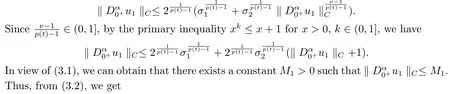
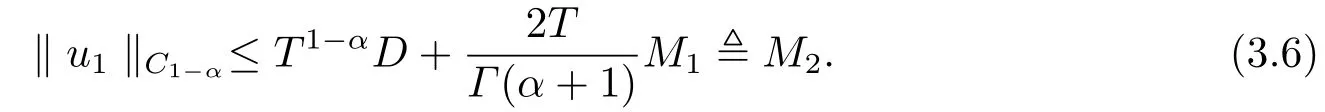
From the second equation of (3.3), the Caputo fractional derivative and Riemann-Liouville fractional integral, we have

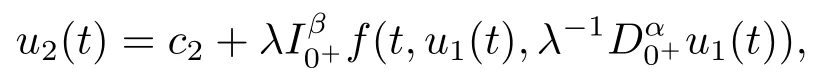
which together withu2(ξ)=0 yields

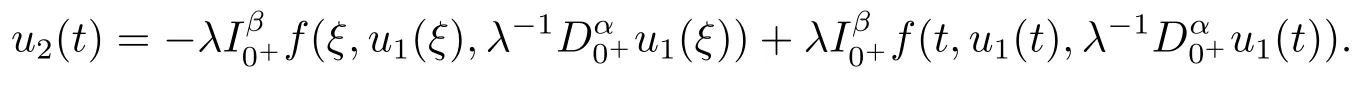
Then we get

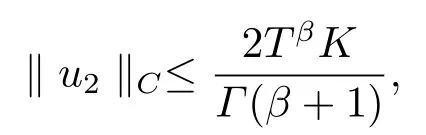
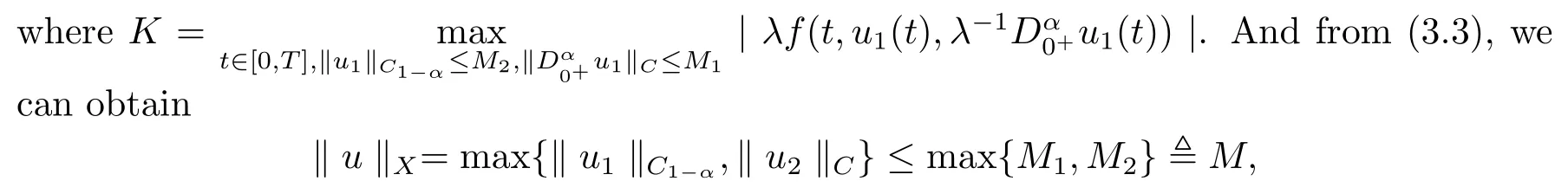
which meansΩ1is bounded.

LetΩ2={u ∈KerL|QNu=0}.Foru ∈Ω2,we haveu1(t)=c1,u2(t)=c2,?c1,c2∈R.Then we get

From the first equality, we getc2= 0.And from the second equality and (H2), we have|c1|≤D.Hence,‖u‖X=max{|c1|,|c2|}≤D,Thus,Ω2is bounded.

From the condition (H2), one has

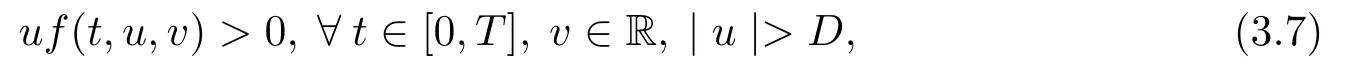
or

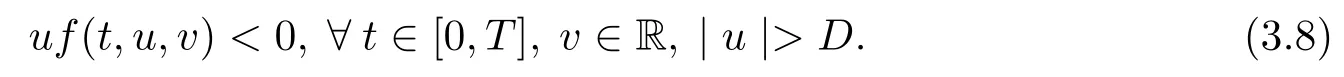
When (3.7) holds, define the operatorJ:ImQ →KerLby

J(u1,u2)T=(±u2,u1)T,

and let

Ω3={u ∈Ker|λu+(1?λ)JQNu,λ ∈[0,T]}.

Foru ∈Ω3, we haveu1(t)=c1,u2(t)=c2,?c1,c2∈R, and

Ifλ=0,from the first equality of (3.9), we havec2=0.Meanwhile, from the second equality of (3.9) and (3.7), we get| c1|≤D.Ifλ ∈(0,1], we assume| c1|> D.Thus, by (3.7), we obtain

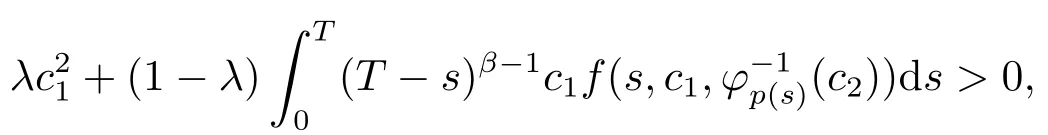
which contradicts the second equality of (3.9).Hence,Ω3is bounded.

When (3.8) holds, let

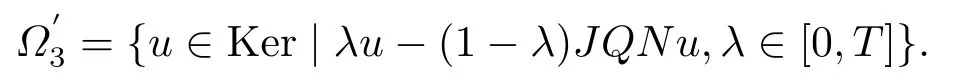
A similar proof can showbounded.

Set

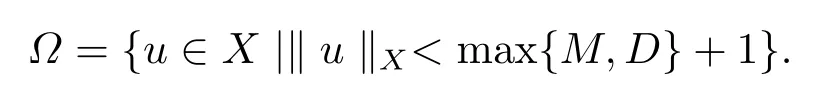
Clearly,Ω1∪Ω2∪Ω3?Ω(orΩ1∪Ω2∪Ω′3?Ω).It follows from Lemma 2.4 and 2.5 thatL(defined by(2.2)is a Fredholm operator of index zero andN(defined by(2.3)isL-compact onMoreover, based on the above proof, the conditions 1) and 2) of Lemma 2.2 are satisfied.

Define the operatorF:[0,T]×Ω →Yby

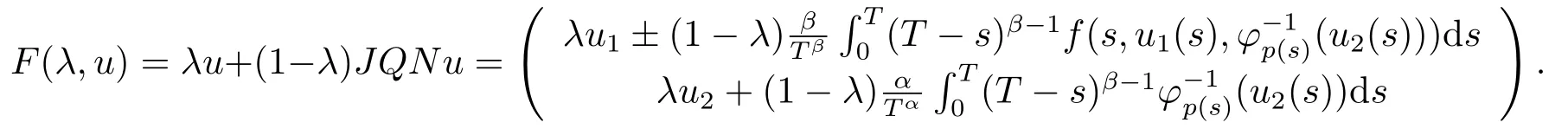
Then, from the above proof, we have

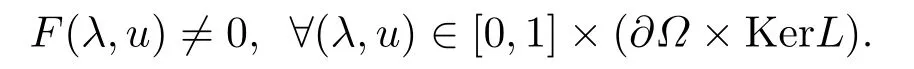
Thus, by the homotopy property of degree, we get

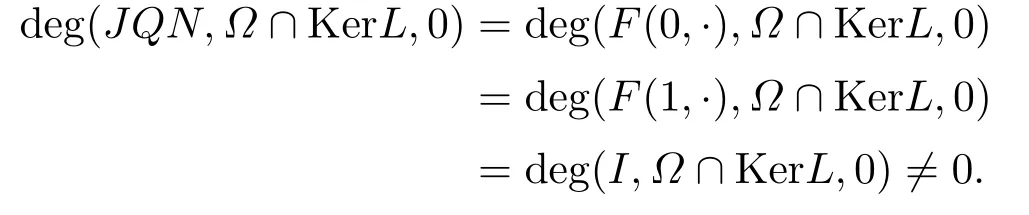
Hence, the condition 3) of Lemma 2.2 is also satisfied.

Therefore,by using Lemma 2.2,the operator equationLx=Nxhas at least one solution in domNamely,the problem(1.2)has at least one solution inX.The proof is complete.

Theorem 3.2Suppose that the condition(H2)holds.Further,assume that the following condition holds.

(H3) there exists a nonnegative numberr ≥0 such that

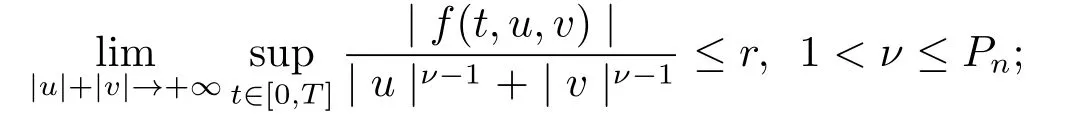
Then, the problem (1.2) has at least one solution, provided that

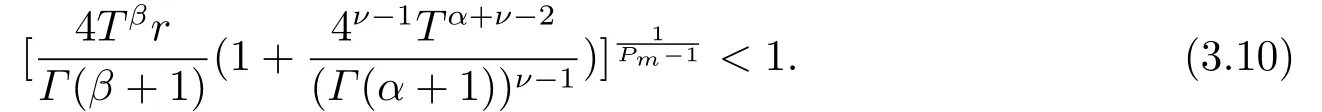
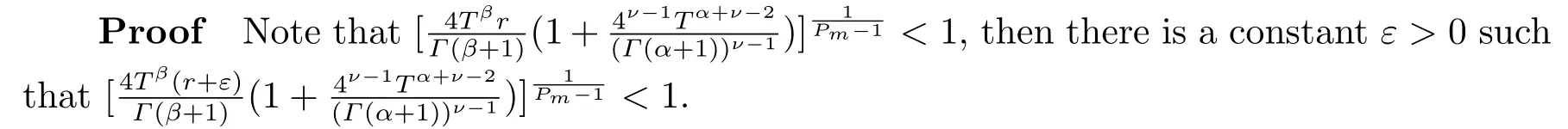
From (H3), there existsH >0 such that

|f(t,u,v)|≤(r+ε)(|u|ν?1+|v |ν?1), |u|+|v |≥H, t ∈[0,T].

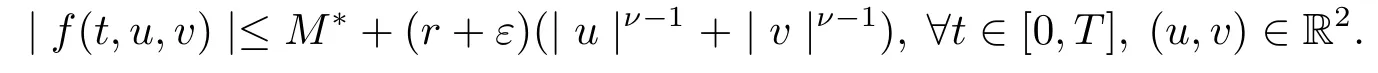
By Theorem 3.1, the problem (1.2) has at least one solution inX.The proof is complete.

Finally, we will present an example to illustrate our main result.

Example 3.1Consider the following mixed fractional periodic boundary value problem withp(t)-Laplacian operator:

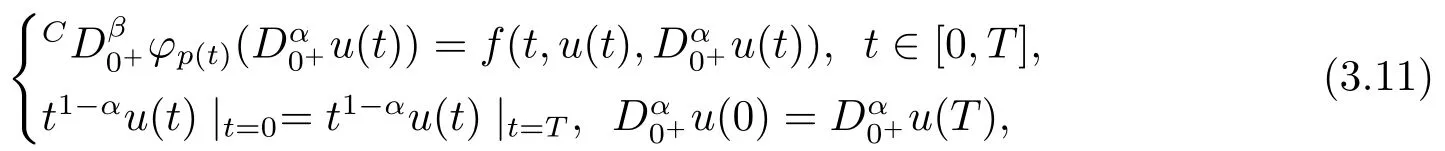
By Theorem 3.1, the problem (3.11) has at least one solution.

Remark 3.1In this paper,we consider the Riemann-Liouville fractional derivativeand Caputo fractional derivativeCin the problem (1.2) simultaneously, which is seldom seen in the existing literatures.Moreover,p(t)-Laplacian operator is relate withtandfis dependent of fractional derivative of unknown functionu(t).So, the obtained results enrich and generalize the existing literatures [8, 11-12, 17-19] and references cited therein, which implies that our results in this paper are new.