環(huán)的余撓維數(shù)

熊濤

(西華師范大學數(shù)學與信息學院, 四川 南充 637002)

1 引言

本文規(guī)定,R恒指有單位元的交換環(huán). 對R- 模N, pdRN代表N的投射維數(shù).用gl.dim(R) (對應地,w.gl.dim(R)) 表示R的整體(對應地, 弱整體) 維數(shù). 對于未解釋的概念和符號, 參考文獻[1-2].

余撓模受到諸多文獻關(guān)注. 文獻[3] 中R- 模C稱為余撓模是指對任何平坦模F,都有Ext1R(F,C) = 0. 每個模都有內(nèi)射包, 與內(nèi)射包相對應的概念是投射蓋. 人們自然要問, 每個模是否有投射蓋. 文獻[4] 證明了每個R- 模有投射蓋當且僅當R是完全環(huán)(每個平坦模是投射模). 隨著蓋包理論的發(fā)展, 文獻[5] 提出了平坦蓋猜測(Flat Cover Conjecture, 縮寫為FCC): 每個R- 模有平坦蓋. 此后, 多篇文獻討論了平坦蓋的存在性. 文獻[6] 借助余撓模, 徹底解決了FCC: 任何環(huán)上, 每個模都有平坦蓋和余撓包.

同調(diào)維數(shù)是刻畫環(huán)的重要工具. 環(huán)R是完全環(huán)是指每個R- 模都有投射蓋, 等價地,每個平坦R- 模是投射模. 文獻[8] 中定義1.1 稱R為n- 完全環(huán)是指每個平坦模的投射維數(shù)不超過n. 文獻[7] 中推論7.2.7 證明了環(huán)R是完全環(huán)當且僅當Cot.D.(R)=0;文獻[7] 中, 推論7.2.6 證明了環(huán)R是n- 完全環(huán)當且僅當Cot.D.(R)≤n.

作為一種新的同調(diào)維數(shù), 自然需要探討, Cot.D.(R) 與經(jīng)典的同調(diào)維數(shù)之間的關(guān)系和差別. 本文探討了這一關(guān)系和差別.

2 環(huán)的余撓維數(shù)

先研究Milnor 方圖上的余撓維數(shù).

說方圖1 是拉回圖(或者笛卡爾方圖) 是指i1與i2是內(nèi)射的, 且j1與j2是滿射.此時規(guī)定R ?T, 且做如下標識

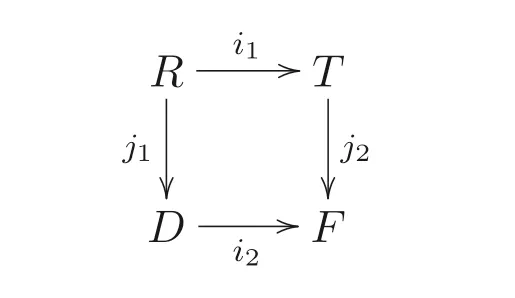
圖1 環(huán)與同態(tài)的交換方圖

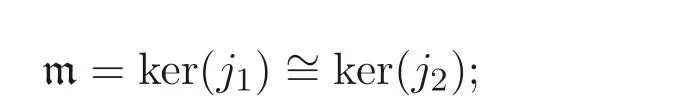
從而, m 是R與T的共同理想, 且滿足D=R/m 與F=T/m. 此時, 笛卡爾方圖便成了如下可記為(□) 的形式:

如果T是整環(huán), m?= 0 是T的極大理想.φ:T →F是自然投射,D是F的真子環(huán), 此時R=φ?1(D). 將這種形式的笛卡爾方圖記為(□?).

在圖2 中, 進行如下特殊化處理: 設(shè)P是D- 模,Q是T- 模, 且設(shè)

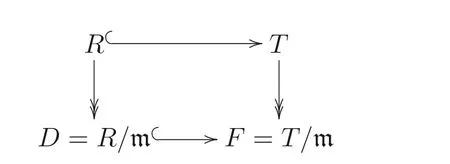
圖2 可記為(□) 的笛卡爾方圖

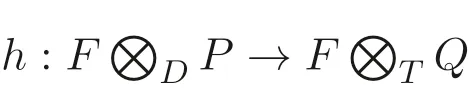
是F- 同構(gòu). 此時, 便出現(xiàn)如下形式的(□) 圖.

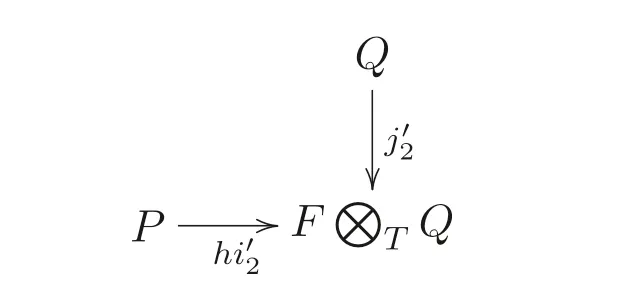
圖3 特殊化處理的(□)

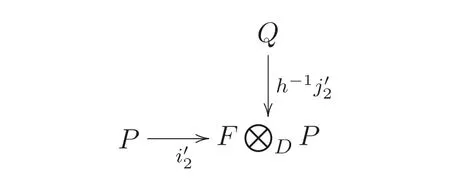
圖4 (□) 經(jīng)過特殊化處理后的對應變化圖

引理2.1對方圖(□), 設(shè)M是如前文提到的R- 模, 則

(1)α是同構(gòu);

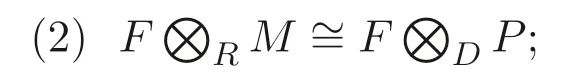
(3) 如果P是平坦D- 模, 或者F是忠實平坦D- 模, 則β是同構(gòu).

故對每個i, 都有(0,vi)∈M. 注意,

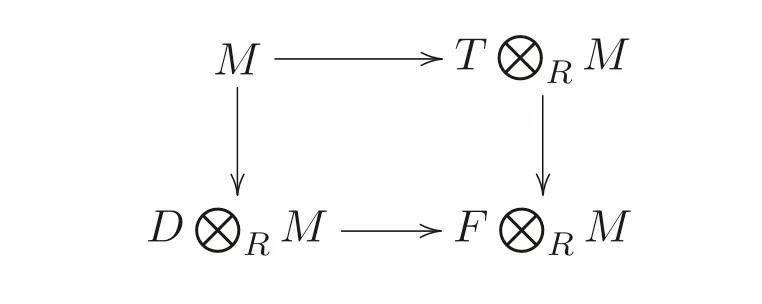
圖5 引理2.1 中(3) 用到的第一個圖

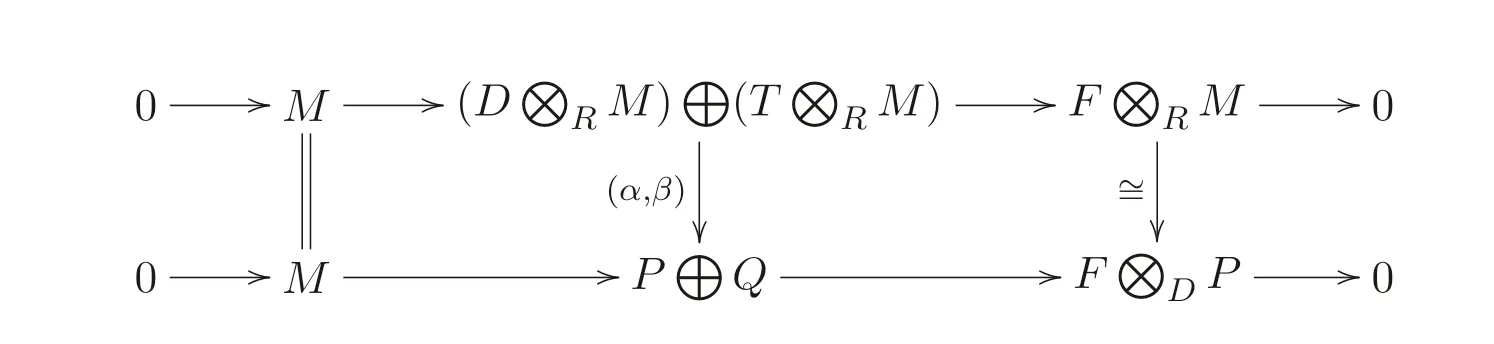
圖6 引理2.1 中(3) 用到的第二個圖

由五引理, (α,β) 是同構(gòu). 故β是同構(gòu).

證畢.

證畢.

定理2.1對方圖(□?), Cot.D(R)≤1 當且僅當Cot.D(D)≤1 與Cot.D(T)≤1成立.

證畢.

推論2.2設(shè)D是整環(huán), 且Cot.D(D)≤1,F是D的商域的擴域. 構(gòu)造環(huán)

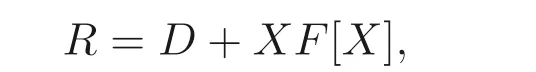
則Cot.D(R)≤1.

遺傳環(huán)是凝聚環(huán), 但滿足Cot.D(R)≤1 的環(huán), 卻未必是凝聚環(huán).

例2.1構(gòu)造環(huán)R= Z+XR[[X]]. 則由定理2.1 可得Cot.D(R)≤1. 又由于[R:Z]=∞, 故由文獻[11] 可知R不是凝聚環(huán).

遺傳環(huán)是Noether 環(huán). 但滿足Cot.D(R)≤1 的凝聚環(huán)卻未必是Noether 環(huán).

例2.2設(shè)X是Q 上的未定元. 構(gòu)造環(huán)R= Z+XQ[X]. 則由文獻[11] 可知R是非Noether 的凝聚整環(huán). 由推論2.2 可知Cot.D(D)≤1.

下面探討環(huán)的余撓整體維數(shù)Cot.D(R) 與整體維數(shù)gl.dim(R) 之間更細致的關(guān)系.

作為余撓模的進一步發(fā)展, 文獻[12] 引入了Warfield 余撓模.R- 模M稱為Warfield 余撓模是指對任何無撓R- 模A, 都有Ext1R(A,M)=0.

引理2.2設(shè)R是整環(huán), 則R是Pr¨ufer 整環(huán)當且僅當每個余撓R- 模是Warfield余撓模.

證明設(shè)M是余撓R- 模. 對任何無撓R- 模N, 由條件,R是Pr¨ufer 整環(huán), 故N是平坦模. 從而Ext1R(N,M)=0, 即M是Warfield 余撓模. 反之, 設(shè)N是無撓R- 模.對任何余撓R- 模M, 由條件,M是Warfield 余撓模. 則Ext1R(N,M)=0 成立. 由文獻[13] 可知,N是平坦模. 故R是Pr¨ufer 整環(huán).

證畢.

引理2.3設(shè)R是整環(huán),U是Warfield 余撓模. 則U的內(nèi)射維數(shù)idRU ≤1.

證明設(shè)M是R- 模, 則存在正合列0→K →P →M →0, 這里P是投射模,K是無撓模. 則Ext2R(M,U)～=Ext1R(K,U)=0 成立, 故idRU ≤1.

證畢.

引理2.4對整環(huán)R, 以下陳述等價:

(1)R是Matlis 整環(huán), 且gl.dim(R)≤2;

(2) 可除模是Warfield 余撓模;

(3)h- 可除模是Warfield 余撓模;

(4) Warfield 余撓模的商模是Warfield 余撓模;

(5) 對任何無撓模N, 都有pdRN ≤1.

證明(1)?(5). 設(shè)N是無撓R- 模, 則存在正合列

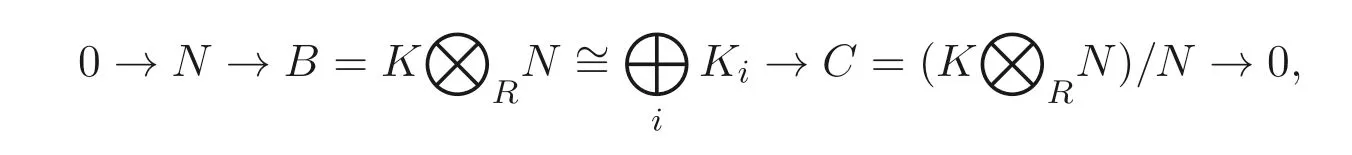
這里每個Ki～=K. 由條件, pdRK ≤1 成立, 故pdRB ≤1 成立. 因此

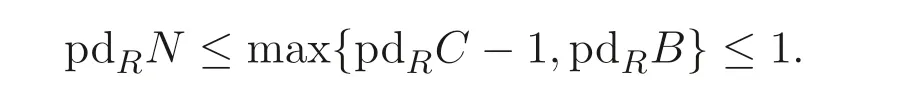
(5)?(3). 設(shè)D是h- 可除R- 模,N是無撓R- 模. 則存在正合列0→A →E →D →0, 這里E是內(nèi)射模. 則由條件, Ext1R(N,D)～= Ext2R(N,A) = 0 成立. 故D是Warfield 余撓模.

(3)?(5). 設(shè)N是無撓模,X是任何R模. 則存在正合列0→X →E →D →0,這里E是內(nèi)射模,D是h- 可除模. 由條件,D是Warfield 余撓模. 則由正合列0 = Ext1R(N,D)→Ext2R(N,X)→Ext2R(N,E) = 0 可得Ext2R(N,X) = 0, 從而pdRN ≤1.

(3)+(5)?(1). 顯然有pdRK ≤1. 故R是Matlis 整環(huán). 對任意R- 模X, 存在正合列0→X →E →D →0, 這里E是內(nèi)射模,D是h- 可除模. 由條件,D是Warfield余撓模. 由引理2.3 可得, idRD ≤1 成立, 故idRX ≤2. 因此gl.dim(R)≤2.

(1)+(3)?(2)?(3). 顯然.

(3)?(4). 設(shè)M是Warfield 余撓模,C是M的商模. 記A= ker(M →C). 從而0→A →M →C →0 是正合列. 對模A, 存在正合列0→A →E →D →0, 其中E是內(nèi)射模. 從而D是h- 可除模. 考慮如下行是正合列的推出圖的圖7:

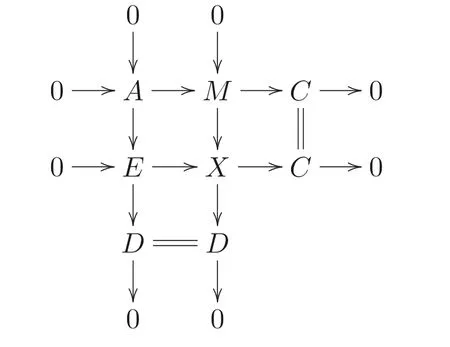
圖7 引理2.4 用到的推出圖

由條件,D是Warfield 余撓模. 設(shè)N是無撓R模. 則序列0 = Ext1R(N,M)→Ext1R(N,X)→Ext1R(N,D) = 0 與Ext1R(N,X)→Ext1R(N,C)→Ext2R(N,E) = 0 是正合列. 故Ext1R(N,C)=0, 即C是Warfield 余撓模.

(4)?(3). 由于內(nèi)射模是Warfield 余撓模, 故結(jié)論成立.

證畢.

引理2.51- 完全整環(huán)R是Matlis 整環(huán). 故整環(huán)R是1- 完全整環(huán)當且僅當可除模是余撓模, 當且僅當每個h- 可除模是余撓模.

證明由于Cot.D(R)≤1, 故其商域K滿足pdRK ≤1 成立, 即R是Matlis 整環(huán).

證畢.

定理2.2設(shè)R是Pr¨ufer 整環(huán), 則Cot.D(R)≤1 當且僅當R是Matlis 整環(huán),且gl.dim(R)≤2.

證明設(shè)Cot.D(R)≤1 成立, 則由引理2.5 可知,R是Matlis 整環(huán). 設(shè)X是任意R- 模, 則存在正合列0→X →E →C →0, 這里E是內(nèi)射模,C是h- 可除模. 則再由引理2.5 可知C是余撓模. 由引理2.2 和引理2.3, idRC ≤1 成立, 即idRX ≤2.從而gl.dim(R)≤2.

反之, 設(shè)R是Matlis 整環(huán), 滿足gl.dim(R)≤2. 設(shè)C是h- 可除模, 由引理2.4 可得,C是Warfield 余撓模, 故C是余撓模. 由引理2.5 可知, Cot.D(R)≤1 成立.

證畢.

現(xiàn)在給出一個滿足Cot.D(R)≤1 的Pr¨ufer 整環(huán)R的例子.

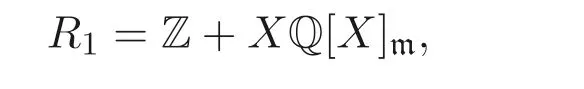
例2.3設(shè)Q 是有理數(shù)域,X是Q 的未定元. 設(shè)m=(X). 構(gòu)造環(huán)這里Z 是整數(shù)集合. 則由文獻[14] 可知R1是Pr¨ufer 整環(huán), Cot.D(R1)≤1. 故R1是Matlis 整環(huán), 且gl.dim(R1)=2.

Matlis 整環(huán)R未必有Cot.D(R)≤1 成立. 為了舉出反例, 給出如下命題:

命題2.1對方圖(□?),R是Matlis 當且僅當T是Matlis 整環(huán).

現(xiàn)在設(shè)T是Matlis 整環(huán), 0→B →P →K →0 是正合列, 且P是投射R- 模. 由于D撓的R- 模, 故D?R K=0 是投射D- 模. 由定理2.1 的證明可知B是投射R-模, 故pdRK≤1. 故R是Matlis 整環(huán).

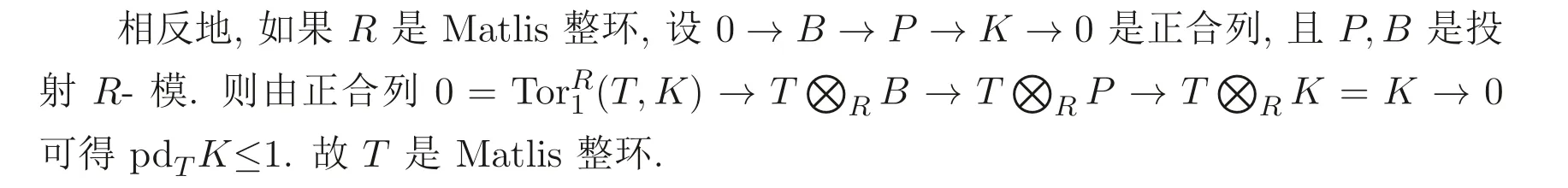
證畢.

例2.4設(shè)D是賦值環(huán), 且gl.dim(R) = 3. 則D是Pr¨ufer 整環(huán), 也是Matlis 整環(huán). 由定理2.2 可得, Cot.D(D)>1 成立. 構(gòu)造環(huán)R=D+XF[X], 這里F是D的商域. 則由命題2.1 可得,R是Matlis 整環(huán). 由定理2.1 可得, Cot.D(R)>1 成立.

以如下反例結(jié)束本文.

一個滿足Cot.D(R)≤1 的整環(huán)未必是Pr¨ufer 整環(huán).

例2.5設(shè)Q 是有理數(shù)域,X是Q 的未定元. 設(shè)m=(X). 構(gòu)造環(huán)

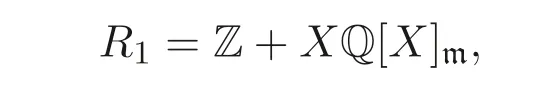
如例2.4, 與R2= Z4, 這里Z 是整數(shù)集合. 再構(gòu)造環(huán)R=R1×R2. 由文獻[14] 可知,Cot.D(R)=1, 且w.gl.dim(R)=∞成立.

當然, 一個整環(huán)滿足w.gl.dim(R)<∞, 也未必有Cot.D(R)≤1.

例2.6設(shè)C(X,Y) 是多項式環(huán)C[X,Y] 的商域. 設(shè)Z是C(X,Y) 上的未定元,且m=(Z). 構(gòu)造環(huán)R1=C[X,Y]+ZC(X,Y)[Z]m, 由文獻[14] 可知,

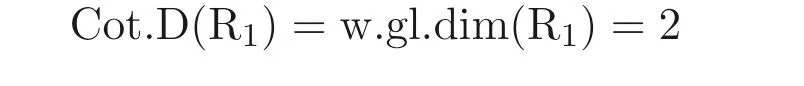
成立.

一個整環(huán)滿足w.gl.dim(R)=∞, 也未必有Cot.D(R)≤1.

例2.7構(gòu)造環(huán)R1=C[X,Y]+ZC(X,Y)[Z]m,如例2.6, 設(shè)R2=Z4, 則R2是完全環(huán), 且w.gl.dim(R2) =∞. 構(gòu)造環(huán)R=R1×R2. 由文獻[14] 可知, Cot.D(R) = 2,w.gl.dim(R)=∞.