冪零奇點的局部可積性及其分類

汪銀姿,胡召平

(上海大學(xué)理學(xué)院, 上海 200444)

平面多項式微分系統(tǒng)的可積問題是微分方程定性理論的核心課題之一, 被劉一戎等[1]列為平面向量場的4 大經(jīng)典問題之一. 盡管一般的系統(tǒng)都是不可積的, 但在研究數(shù)學(xué)模型時可積系統(tǒng)非常重要, 因為對一個可積系統(tǒng)進(jìn)行擾動可以得到豐富的分支現(xiàn)象. 目前, 研究可積問題的成果相當(dāng)多[2-14]. 另外, 退化奇點的分類也是微分方程定性理論的另一個重要課題. 韓茂安[15]對平面哈密頓系統(tǒng)的冪零奇點給出了一個有效的分類方法, 而這里的冪零奇點是一類特殊的退化奇點. 可見, 哈密頓系統(tǒng)只是一類特殊的可積系統(tǒng), 目前也有相當(dāng)多的學(xué)者研究哈密頓系統(tǒng)[16-22].

中心問題是另一個和可積性問題密切相關(guān)的經(jīng)典問題, 也是同屬于平面向量場理論中的4 大經(jīng)典問題之一[1]. 所謂的中心問題是, 在什么條件下平面實多項式系統(tǒng)

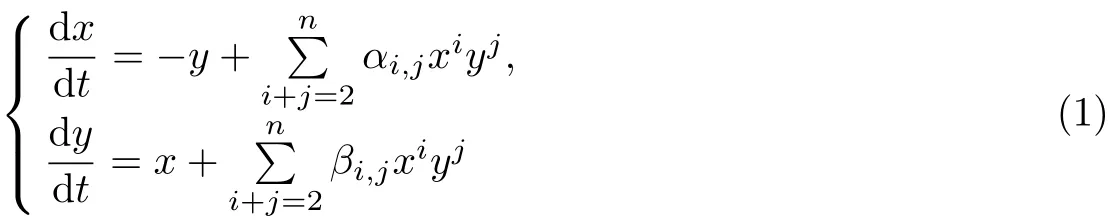
以原點(0,0)為中心? 眾所周知, 原點(0,0)為系統(tǒng)(1)的中心當(dāng)且僅當(dāng)具有如下形式的首次積分:

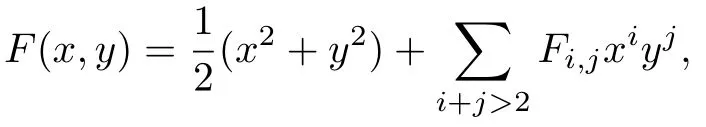
即函數(shù)F(x,y)滿足方程

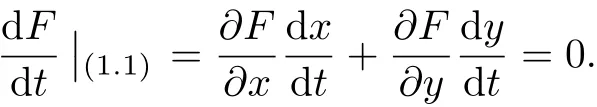
引入變換u=x+iy,v=, i dt=dτ, 并仍記τ為t, 則系統(tǒng)(1)變?yōu)槿缦聫?fù)平面上的多項式微分系統(tǒng):

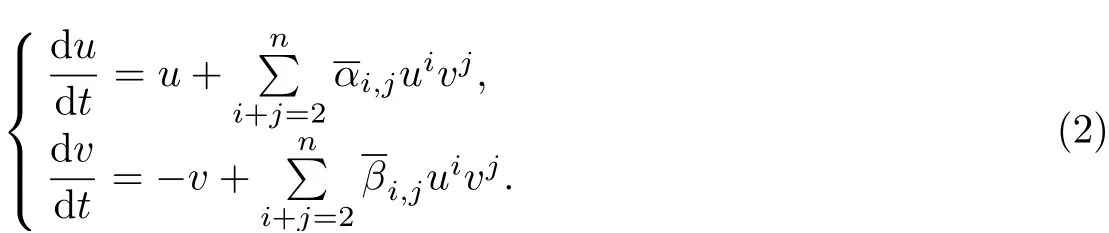
因而, 中心問題等價于系統(tǒng)(2), 具有如下的首次積分:

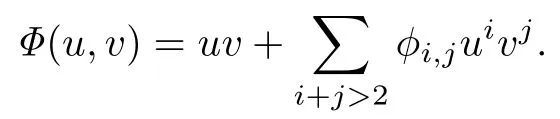
此時, 稱原點為系統(tǒng)(2)的1:-1 共振中心.

進(jìn)一步地, 該問題可以推廣到如下更一般的復(fù)系統(tǒng):

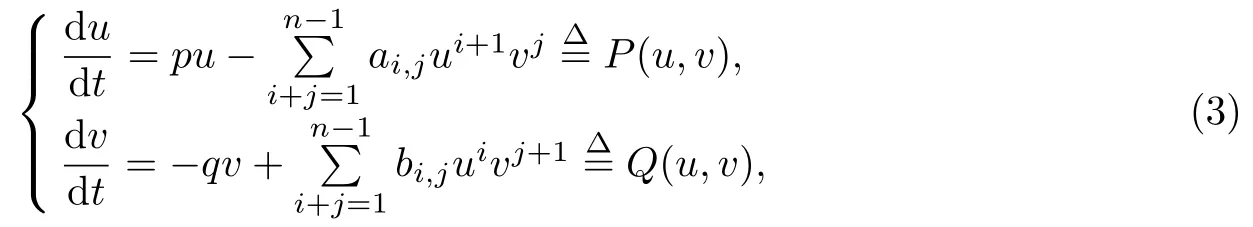
式中:p,q ∈N 且互素, 并將高次項的系數(shù)記為

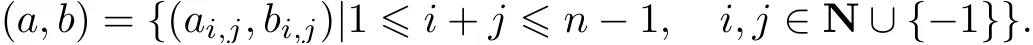
若系統(tǒng)(3)具有形式

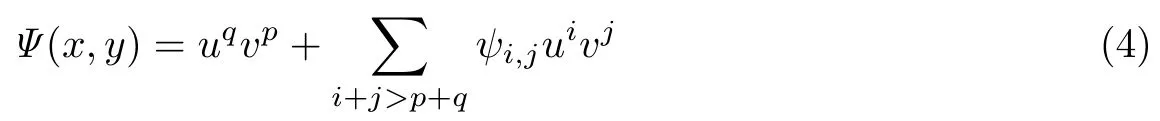
的首次積分, 則稱系統(tǒng)(3)在原點局部可積, 亦稱原點為系統(tǒng)(3)的p:-q共振中心.

由此可見, 上述可積問題可以看作是中心焦點問題的一個推廣, 主要討論實多項式系統(tǒng)的中心焦點和復(fù)多項式系統(tǒng)的p:-q共振中心. 而本工作將討論冪零奇點的局部可積性. 冪零奇點是一類退化奇點, 比中心焦點的情形更復(fù)雜. 這里將討論平面實系統(tǒng)

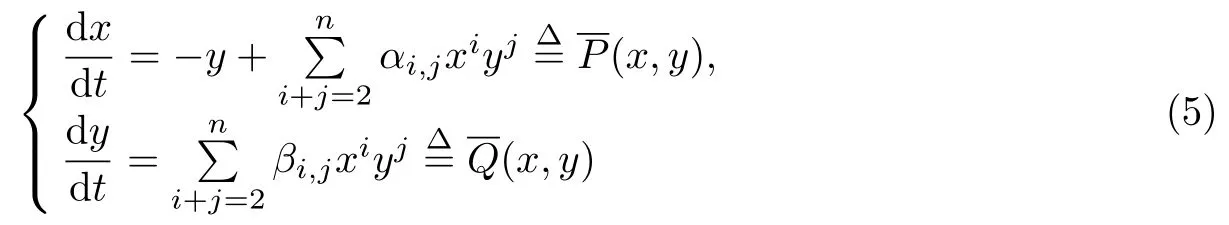
的局部可積性, 并在可積條件下討論冪零奇點(0,0)的完全分類問題.

1 準(zhǔn)備工作

1.1 局部可積性問題

系統(tǒng)(3)以原點為p:-q共振中心當(dāng)且僅當(dāng)系統(tǒng)具有形如系統(tǒng)(4)的首次積分. 因此,

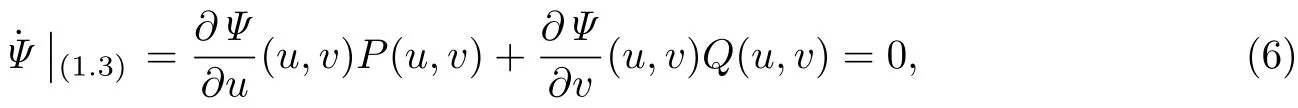
即

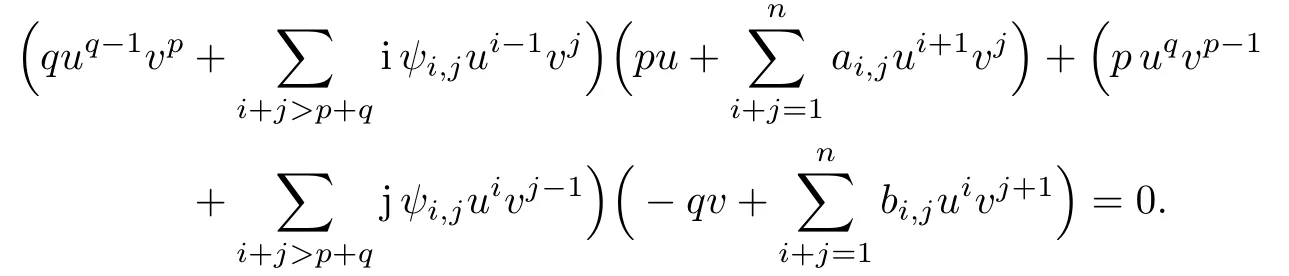
記gk1,k2為上式左端uk1+qvk2+p項的系數(shù), 則有

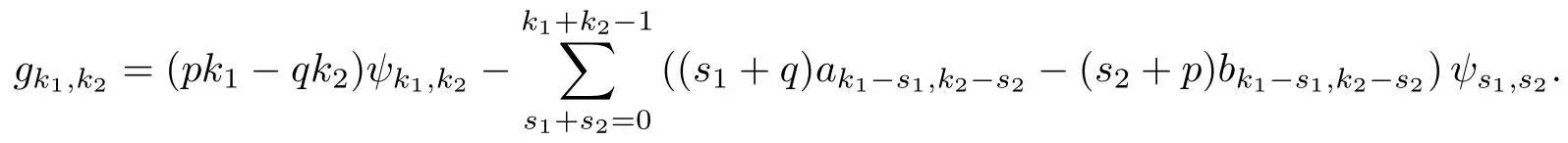
若pk1-qk2=0, 且k1=kq, k2=kp, k ∈N, 則

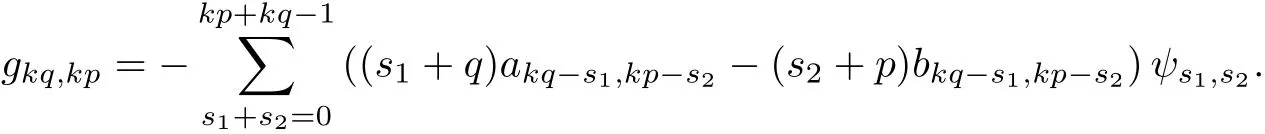
多項式gkq,kp稱為系統(tǒng)(3)的第k個可積量, 記作ik(a,b). 顯然, 系統(tǒng)(3)可積當(dāng)且僅當(dāng)所有的可積量ik(a,b)均為0. 由所有的可積量生成的理想I=＜i1,i2,··· ,ik,··· ＞稱為Bautin 理想, 而其簇類

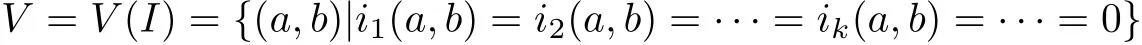
稱為系統(tǒng)(3)的可積簇. 因此,系統(tǒng)(3)可積的充要條件即為V. 進(jìn)一步,記Ik=＜i1,i2,···,ik ＞,且Vk=V(Ik), 易知

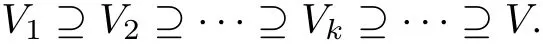
由Hilbert 有限基定理可知, 存在有限的自然數(shù)N, 使得I=IN, 從而V=V(IN) =VN.這就使得通過得到有限可積量就找到系統(tǒng)可積的充要條件成為可能. 然而, 可積問題最大的障礙就在于如何得到盡可能多的可積量, 以及如何保證這些可積量是足夠的. 為此, 通過Romanovski 等[13]給出的Singular 代數(shù)編程中的minAssGTZ 算法, 可以將這N個可積量構(gòu)成的簇類分解為若干個不可約集C1,C2,··· ,Cm, 即

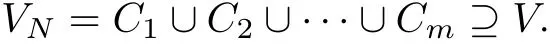
這樣, 系統(tǒng)(3)可積的必要條件就是系數(shù)(a,b)至少包含在C1,C2,··· ,Cm中某個集合內(nèi).

接下來, 還需要證明上述條件急必要還是充分的, 即VN=C1∪C2∪···∪Cm ?V. 也就是說, 僅需要證明在每個條件Ck(1 ≤k≤m)下系統(tǒng)(3)是可積的, 即Ck ?V.

目前, 已有不少方法被用來證明系統(tǒng)(3)可積的充分性(如時間可逆性)、Darboux 首次積分法等. 在這里, 僅簡略介紹Romanovski 等[13]給出的Darboux 首次積分法的幾個結(jié)論.

定義1[13]對于系統(tǒng)(3), 若存在函數(shù)f(u,v)及多項式函數(shù)k(u,v), 使得

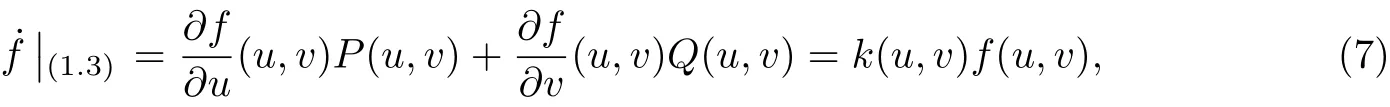
則稱函數(shù)f(u,v)為系統(tǒng)(3)的一個Darboux 因子, 而k(u,v)稱為對應(yīng)的余因式.

為了構(gòu)造系統(tǒng)(3)的一個Darboux 首次積分, 有如下的定理.

定理1[13]若系統(tǒng)(3)有Darboux 因子f1,f2,··· ,fm, 且對應(yīng)的余因式k1,k2,··· ,km滿足條件

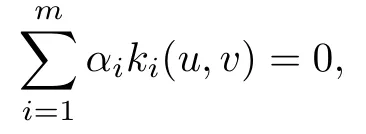
則Φ=為系統(tǒng)(3)的一個Darboux 首次積分; 若滿足

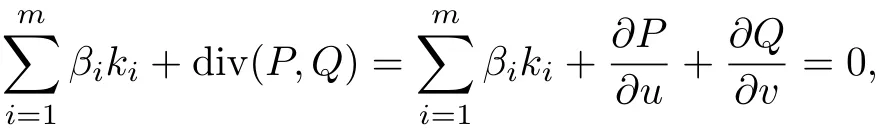
則系統(tǒng)(3)有一個Darboux 積分因子

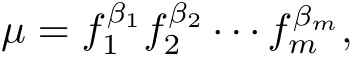
故系統(tǒng)(3)可積.

由此不難看出, 研究多項式微分系統(tǒng)(3)的可積問題可以遵循如下步驟:

步驟1 利用Mathematica 等數(shù)學(xué)編程軟件, 盡可能多地計算出系統(tǒng)(3)的前若干個可積量ik(a,b),k=1,2,··· ,N0;

步驟2 由minAssGTZ 算法將簇類VN0={(a,b)|i1(a,b) =i2(a,b) =···=iN0(a,b) =0}分解為若干不可約的集合C1,C2,··· ,Cm的并;

步驟3 在每個條件Ci下, 證明系統(tǒng)(3)是可積的,i=1,2,··· ,m.

1.2 冪零奇點的分類

在平面向量場理論中, 冪零奇點是指該奇點對應(yīng)的線性近似系統(tǒng)的系數(shù)矩陣本身是非零矩陣而平方為零矩陣的情形. 顯然, 冪零奇點是退化奇點的一個特殊情況. 此時, 該系數(shù)矩陣以0 為二重特征值, 對應(yīng)的標(biāo)準(zhǔn)型矩陣為一個若當(dāng)塊. 而退化奇點在添加非線性項的情形下將變得非常復(fù)雜. 目前, 有不少關(guān)于退化奇點的討論, 但給出完整分類結(jié)果的非常少, 僅有韓茂安[15]對平面哈密頓系統(tǒng)的冪零奇點提出了一個行之有效的方法, 并得到了完整的分類結(jié)果.

考慮平面多項式哈密頓系統(tǒng)

其對應(yīng)的哈密頓函數(shù)為

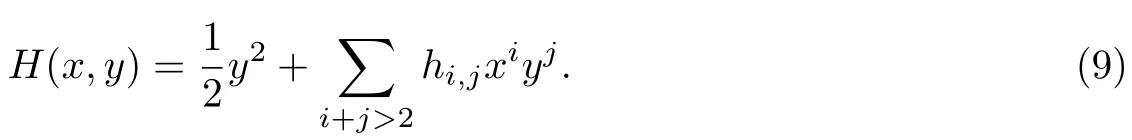
易知Hyy(0,0) = 1. 由隱函數(shù)定理可知, 當(dāng)|x|充分小時, 方程Hy(x,y) = 0 有唯一的解析解y=φ(x)=O(x2). 通過計算易得

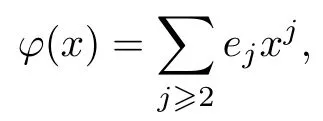
其中

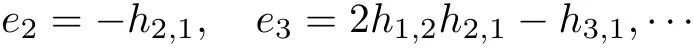
故將解y=φ(x)代入哈密頓函數(shù)H(x,y)并泰勒展開可得

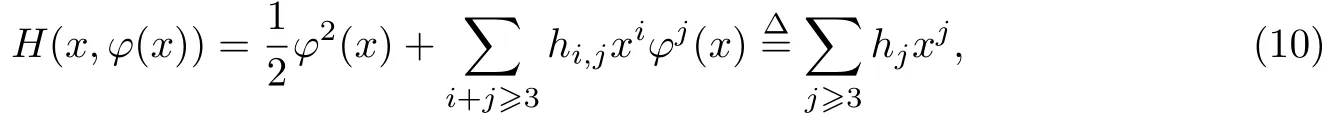
其中

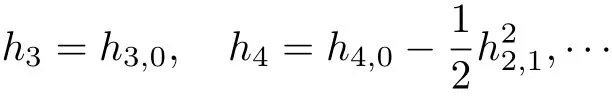
令k≥3 滿足條件

則有如下的結(jié)論.

定理2[15]對于系統(tǒng)(8), 設(shè)系統(tǒng)(10)和(11)成立, 則

(i) 若k為奇數(shù), 則原點為系統(tǒng)(8)的一個尖點;

(ii) 若k為偶數(shù)且hk ＜0, 則原點為系統(tǒng)(8)的一個鞍點;

(iii) 若k為偶數(shù)且hk ＞0, 則原點為系統(tǒng)(8)的一個中心.

定理3[15]對于系統(tǒng)(8), 設(shè)系統(tǒng)(10)和(11)成立. 則

(i) 當(dāng)k=2m+1 時, 原點稱為系統(tǒng)(8)的一個m階冪零尖點;

(ii) 當(dāng)k=2m+2 且hk ＞0 時, 原點稱為系統(tǒng)(8)的一個m階冪零中心;

(iii) 當(dāng)k=2m+2 且hk ＜0 時, 原點稱為系統(tǒng)(8)的一個m階冪零鞍點.

2 幾個推廣的結(jié)果

考慮如下的平面實多項式微分系統(tǒng)

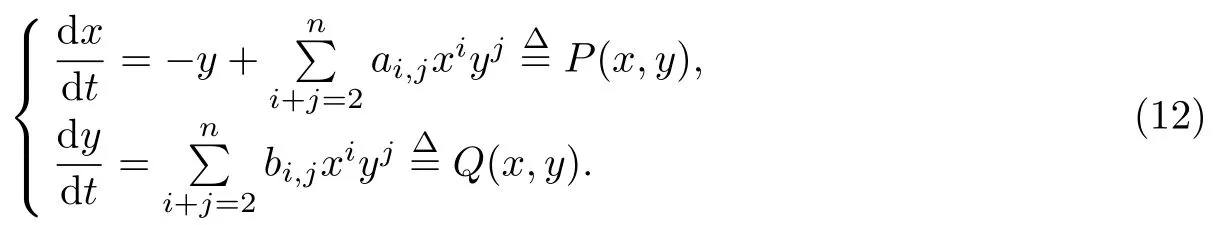
若系統(tǒng)(12)有如下的首次積分

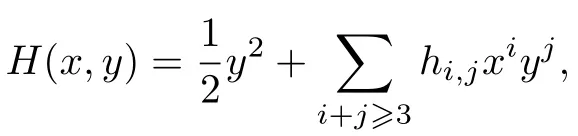
則稱系統(tǒng)(12)在原點是局部可積的. 此時, 有

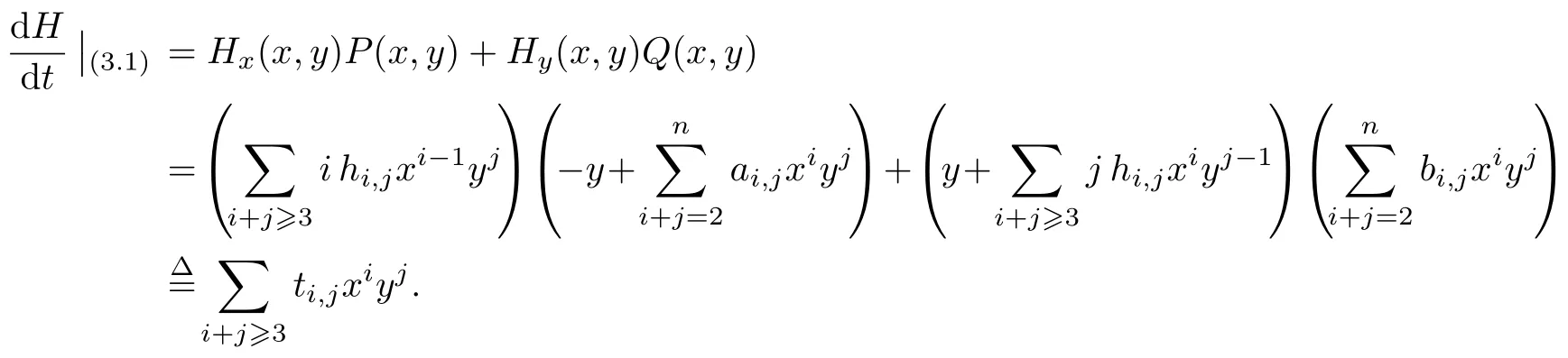
通過計算可得

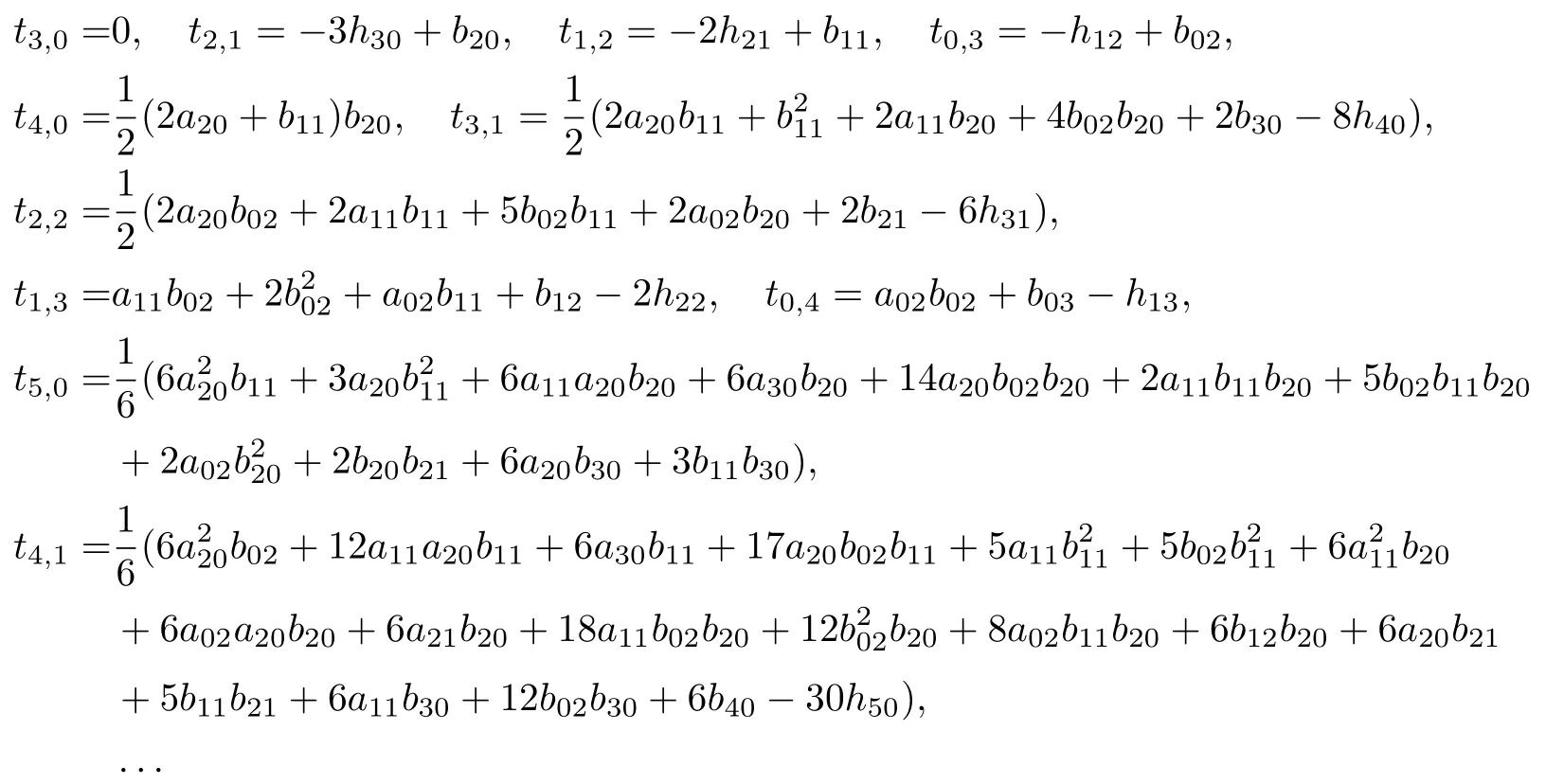
顯然, 函數(shù)H(x,y)為系統(tǒng)(12)的首次積分當(dāng)且僅當(dāng)所有的ti,j=0 成立. 求解方程組ti,j=0,可以看出如下的項均必須為0:

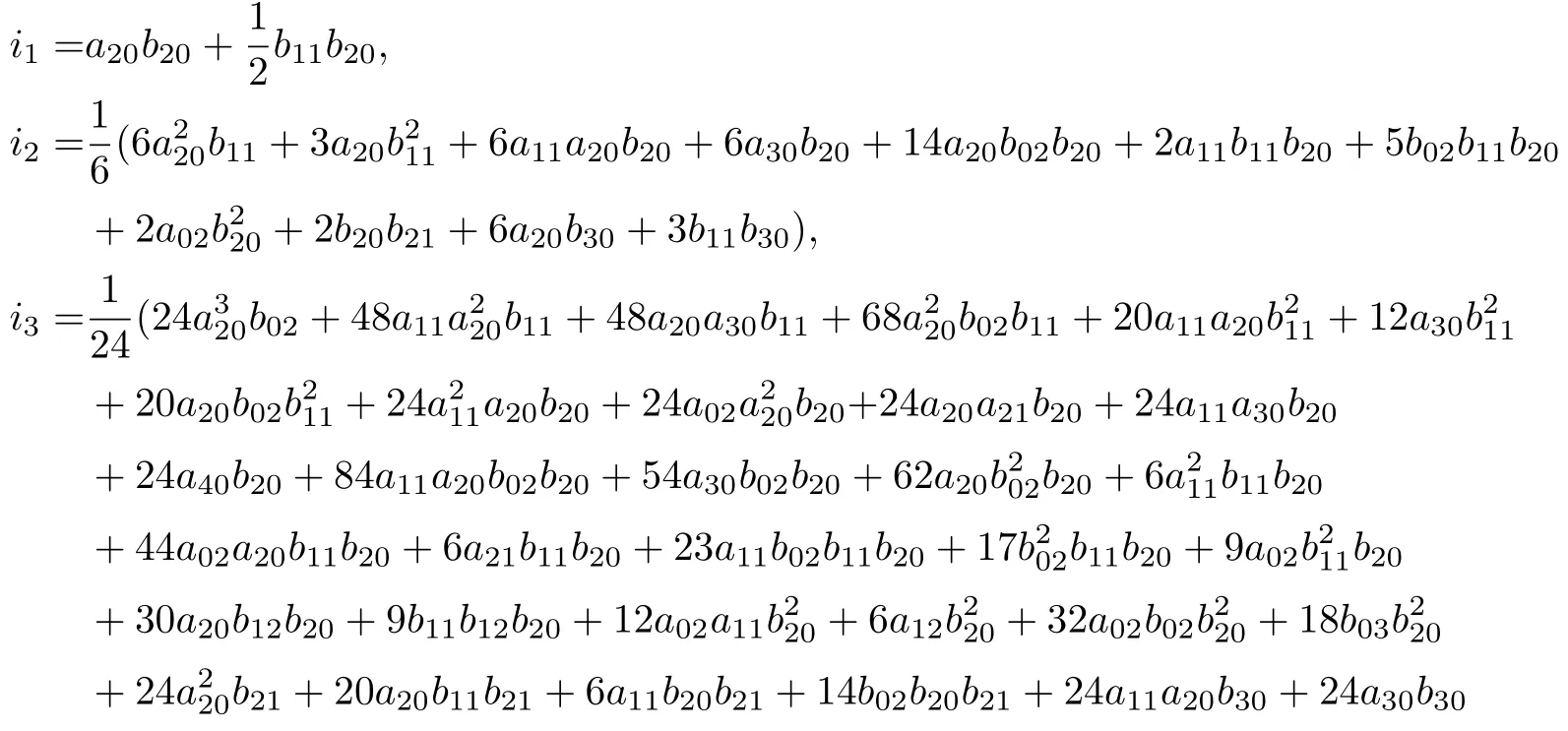
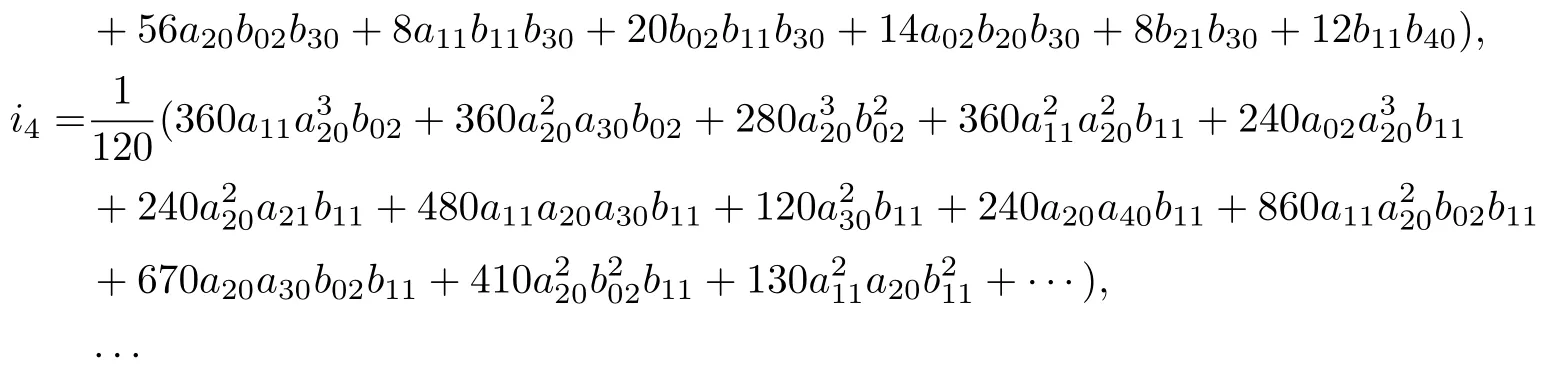
類似地, 稱ik(a,b)為系統(tǒng)(12)的第k個可積量.

如果找到了系統(tǒng)(12)的前N個可積量i1,i2,··· ,iN, 那么就找到了系統(tǒng)(12)可積的一個必要條件:

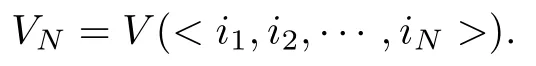
進(jìn)一步地, 如果N足夠大且V=VN, 就得到了系統(tǒng)(12)可積的充要條件V. 類似于第2 節(jié)中處理VN的方法, 并且關(guān)于可積充分性的結(jié)論對系統(tǒng)(12)仍然是成立的. 因此, 可遵循第2 節(jié)中的3 個步驟來研究系統(tǒng)(12)的局部可積性.

現(xiàn)在, 研究系統(tǒng)(12)在原點局部可積的條件下冪零奇點(0,0)的分類問題. 顯然, 系統(tǒng)(12)有首次積分

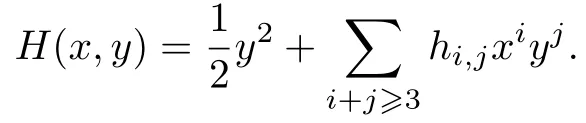
若存在滿足條件μ(0,0)/=0 的函數(shù)μ(x,y), 使得

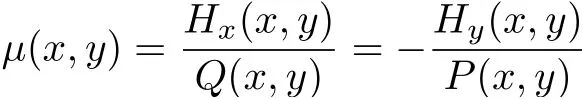
成立, 則μ(x,y)稱為系統(tǒng)(12)的一個積分因子. 引入變換t=μ(x,y)τ, 系統(tǒng)(12)可化為如下的哈密頓系統(tǒng)

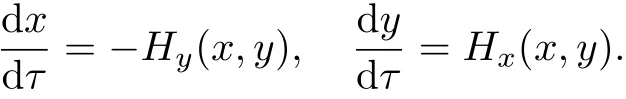
然而, 目前可積系統(tǒng)的積分因子μ(x,y)存在性問題仍然是一個公開的問題. 韓茂安[23]對系統(tǒng)(1)給出了一個積分因子μ(x,y)存在性的證明.

定理4[23]若系統(tǒng)(1)以原點為中心, 則存在解析函數(shù)H(x,y)=x2+y2+···, 且滿足條件μ(0,0)/=0 的函數(shù)μ(x,y), 使得系統(tǒng)(1)可寫為

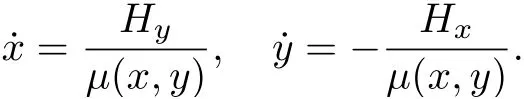
對于原點為p:-q共振中心或冪零奇點的可積系統(tǒng), 不能證明μ(x,y)的存在性, 但是也從未發(fā)現(xiàn)可積系統(tǒng)無積分因子的反例. 若找到了滿足條件μ(0,0)/= 0 的積分因子μ(x,y), 則系統(tǒng)(12)在原點附近與對應(yīng)的哈密頓系統(tǒng)是拓?fù)渫瑯?gòu)的. 因此, 可以由韓茂安[15]研究哈密頓系統(tǒng)冪零奇點的方法, 給出可積系統(tǒng)(12)的冪零奇點(0,0)的分類結(jié)果.

3 帶冪零奇點的2 次系統(tǒng)

對于如下2 次系統(tǒng)

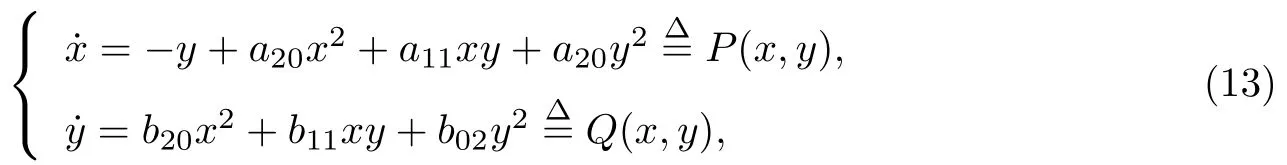
這里將討論系統(tǒng)(13)在原點的局部可積性, 并在每個可積的條件下討論冪零奇點(0,0)的完整分類情況.

3.1 可積條件

定理5系統(tǒng)(13)可積當(dāng)且僅當(dāng)下列條件之一成立:

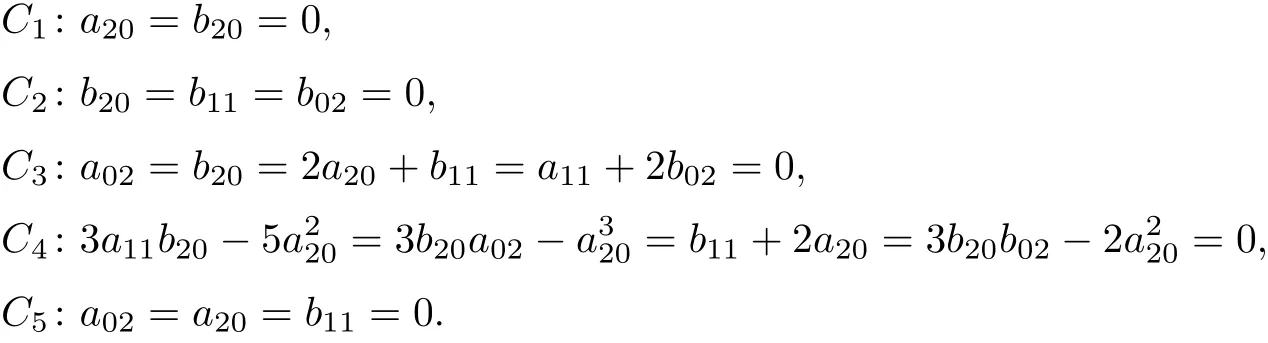
證明 首先證明必要性.

運用Mathematica 編程計算系統(tǒng)(13)的可積量, 易得i1=b20(2a20+b11). 由于計算比較復(fù)雜, 故分b20=0 和b20/=0 這2 種情況分別計算可積量. 得到了b20=0 情形下的前5 個可積量i1,i2,i3,i4,i5和b20/=0 情形下的前5 個可積量i*1,i*2,i*3,i*4,i*5如下:

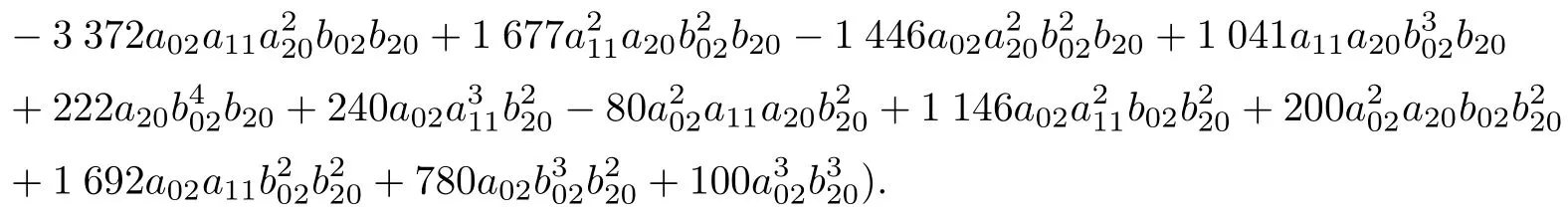
由此可見,

這里,V(＜i1,i2,i3,i4,i5＞)和V(＜,1-λb20＞)各表示i1=i2=i3=i4=i5= 0 和= 0,b20/= 0 的解. 利用minAssGTZ 程序?qū)5進(jìn)行不可約分解, 得到了5 個不可約集, 即分別滿足定理中條件C1,C2,C3,C4和C5的解集, 仍記為C1,C2,C3,C4和C5, 從而得到

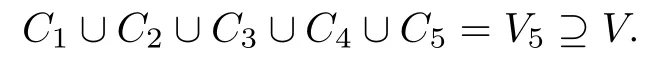
必要性得證.

下面證明充分性, 即C1∪C2∪C3∪C4∪C5=V5?V.

C1: 此時, 系統(tǒng)(13)可化為

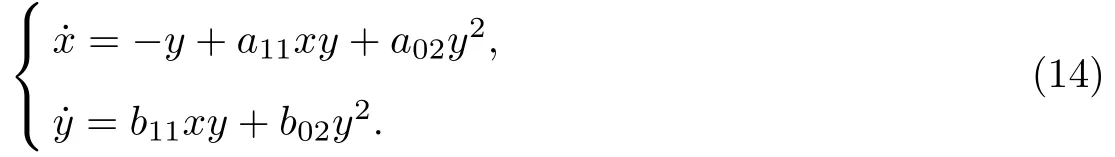
設(shè)系統(tǒng)(14)存在Darboux 因子f(x,y)和對應(yīng)的余因式k(x,y)分別為

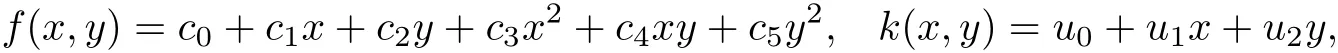
由定義1 有

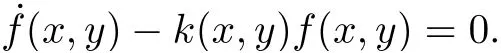
求解可得系統(tǒng)(14)有2 個Darboux 因子f1(x,y)=y和

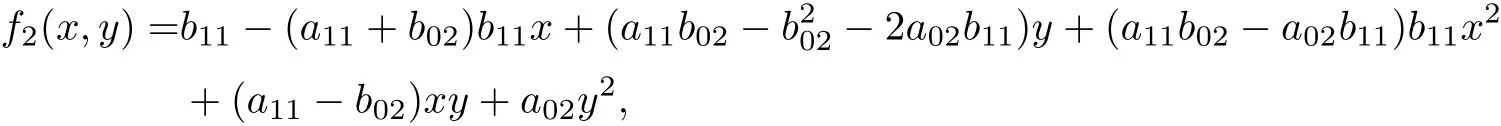
對應(yīng)的余因式分別為

而系統(tǒng)(14)的發(fā)散量為

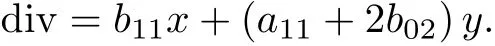
解方程

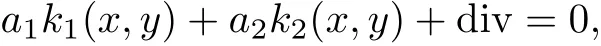
可得a1=a2=-1. 因此, 由定理1 可知系統(tǒng)(14)有積分因子

從而系統(tǒng)(14)可積.

C2: 此時, ˙y=0, 系統(tǒng)(13)顯然可積.

C3: 此時, 系統(tǒng)(13)為哈密頓系統(tǒng), 故必可積.

C4: 若b20= 0, 則為C3的情形. 故僅考慮b20/= 0 的情形. 不失一般性, 不妨設(shè)b20= 1,則系統(tǒng)(13)變?yōu)?/p>

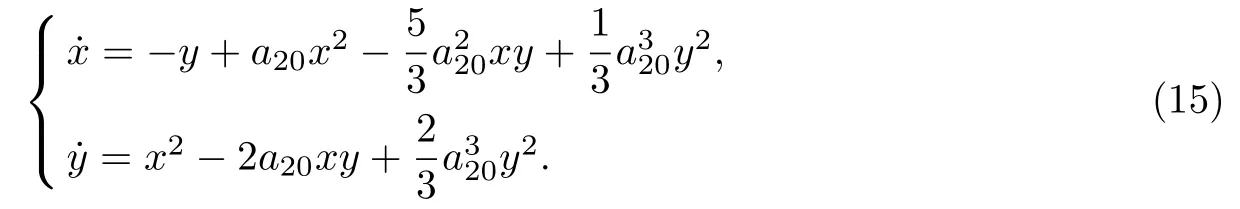
系統(tǒng)(15)中的Darboux 因子和余因式分別為

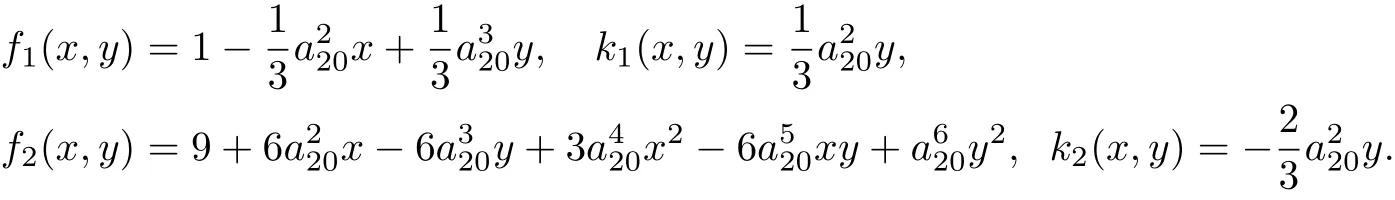
由定理1, 可得系統(tǒng)(15)有首次積分

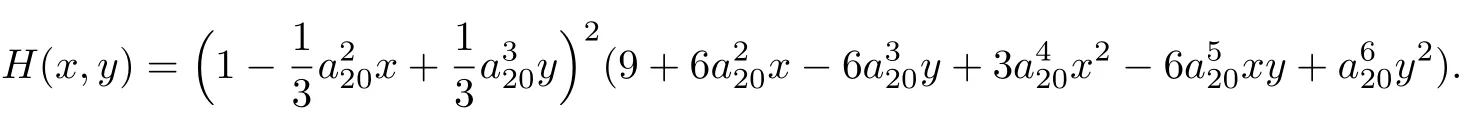
因此, 該系統(tǒng)可積.

C5: 此時, 系統(tǒng)(13)可以寫為

該系統(tǒng)有Darboux 因子f(x,y)=1-a11x, 對應(yīng)的余因式為k(x,y)=a11y.

另一方面, 系統(tǒng)(16)的發(fā)散量為(a11+2b02)y. 由定理1, 可得該系統(tǒng)有積分因子

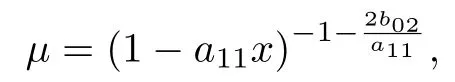
故系統(tǒng)(16)可積.

綜上所述, 有V=C1∪C2∪C3∪C4∪C5.

3.2 冪零奇點的分類

考慮系統(tǒng)(13)可積時相應(yīng)的冪零奇點的分類情況. 顯然, 條件C1或C2下系統(tǒng)的原點為非孤立奇點, 故不予考慮; 而條件C3下系統(tǒng)(13)為哈密頓系統(tǒng)

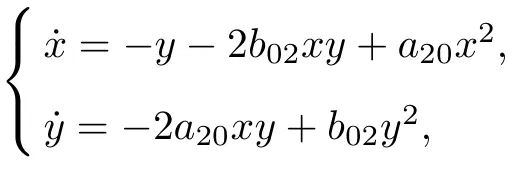
對應(yīng)的哈密頓函數(shù)為

這是一個2 次哈密頓系統(tǒng), 韓茂安[15]已經(jīng)給出了該系統(tǒng)原點詳細(xì)的分類情況.

對于條件C4和C5的情形, 有如下的結(jié)論.

定理6條件C4下的系統(tǒng)(13)為

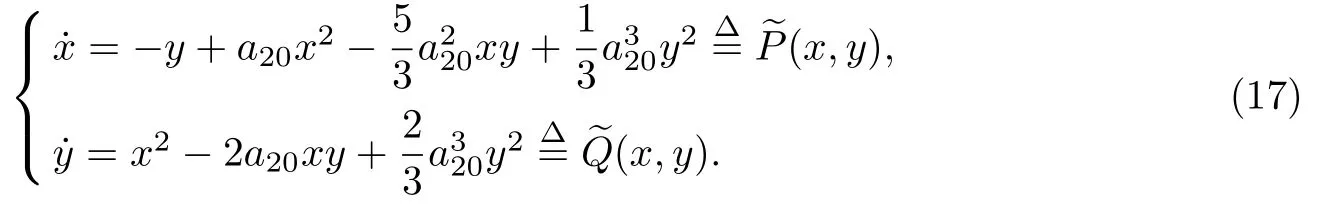
此時, 原點必為尖點, 且階數(shù)為1.

證明 由定理5 可知, 系統(tǒng)(17)有首次積分

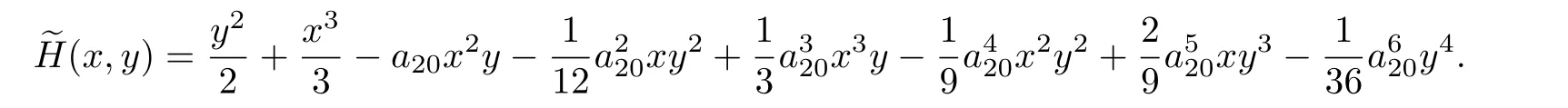
從而可得系統(tǒng)(17)的一個積分因子

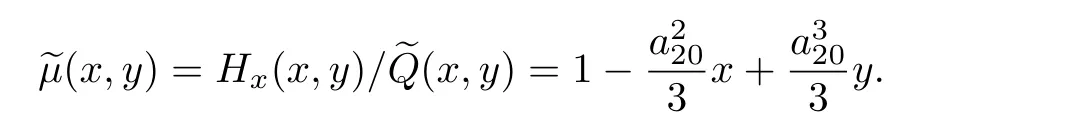
因此, 系統(tǒng)(17)等價于如下的哈密頓系統(tǒng):

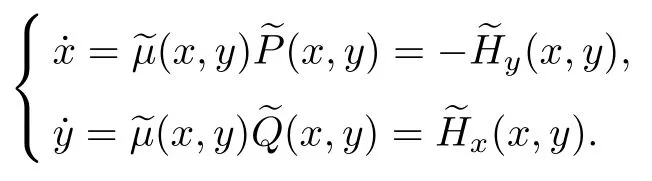
由隱函數(shù)定理可知, 當(dāng)|x|充分小時方程Hy(x,y)=0 有唯一的解析解

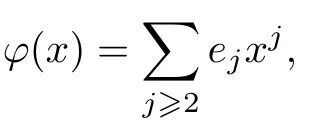
式中,

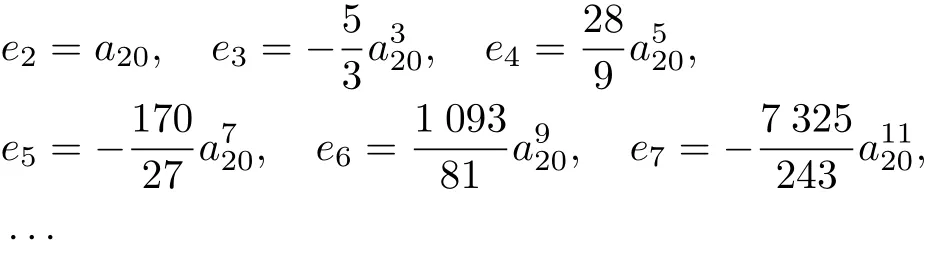
因此,

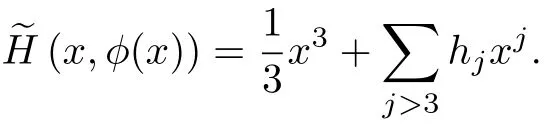
由定理2 及3 可知, 原點必為1 階尖點.

定理7條件C5下的系統(tǒng)(13)為

當(dāng)b20/=0 時, 原點為1 階尖點; 當(dāng)b20=0 時, 原點為非孤立奇點.

證明 由定理13 可知, 系統(tǒng)(18)有積分因子

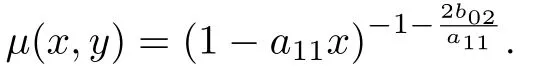
故系統(tǒng)(18)等價于如下的哈密頓系統(tǒng):

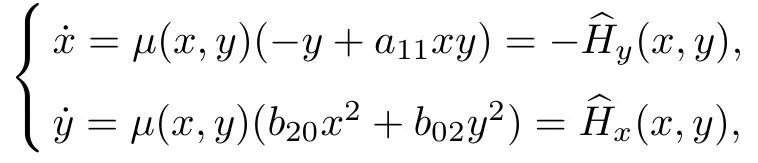
其對應(yīng)的哈密頓函數(shù)為

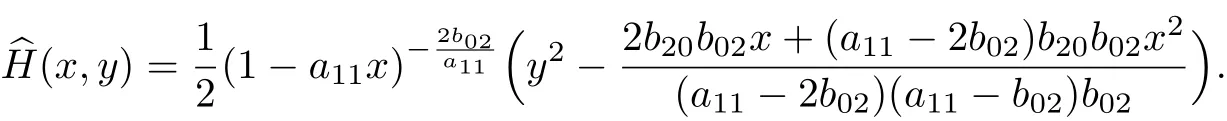
此時, 有φ(x)=0, 且

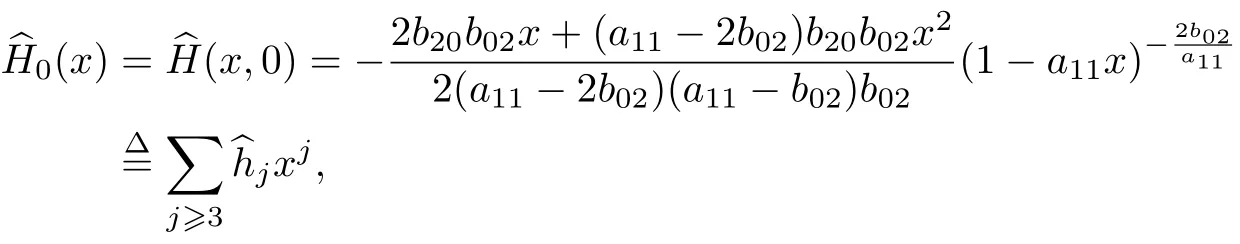
其中,

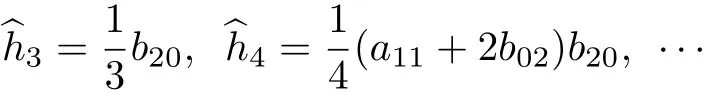
故當(dāng)b20/=0 時,h3/=0, 原點為1 階尖點; 當(dāng)b20=0 時, 直線y=0 上所有的點均為奇點, 即原點為非孤立奇點.

4 含冪零奇點的3 次系統(tǒng)

考慮如下的3 次系統(tǒng)

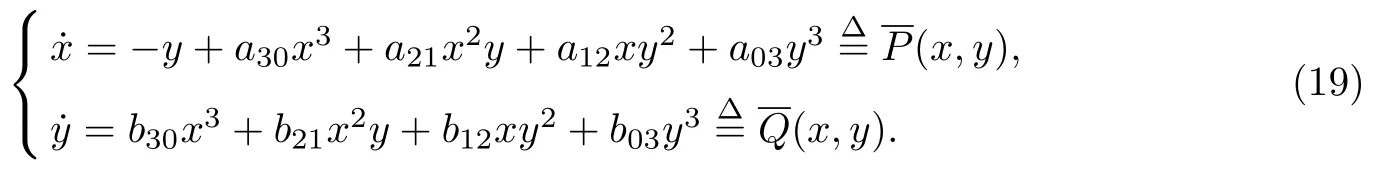
對于系統(tǒng)(19)的局部可積性, 有如下的結(jié)論.

定理8系統(tǒng)(19)可積, 當(dāng)且僅當(dāng)下列條件之一成立:

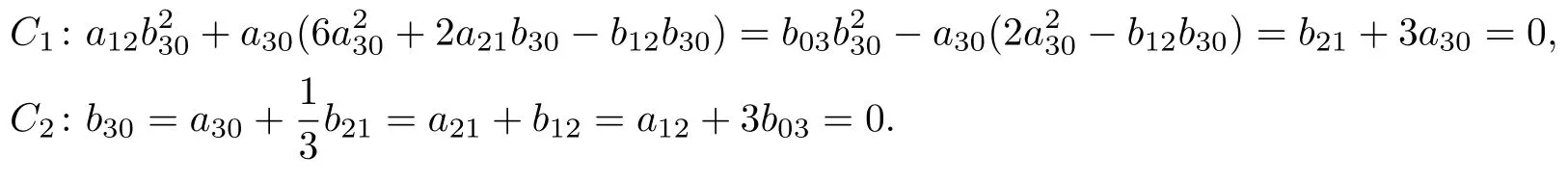
證明 首先證明必要性.

假設(shè)系統(tǒng)(19)有首次積分

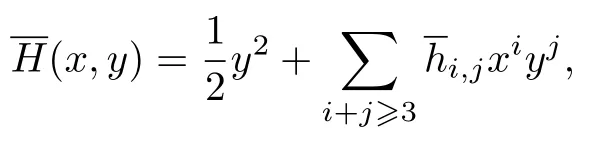
即

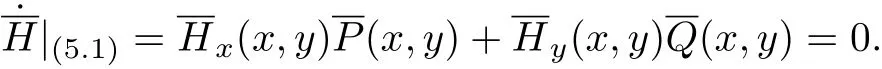
通過計算可知,

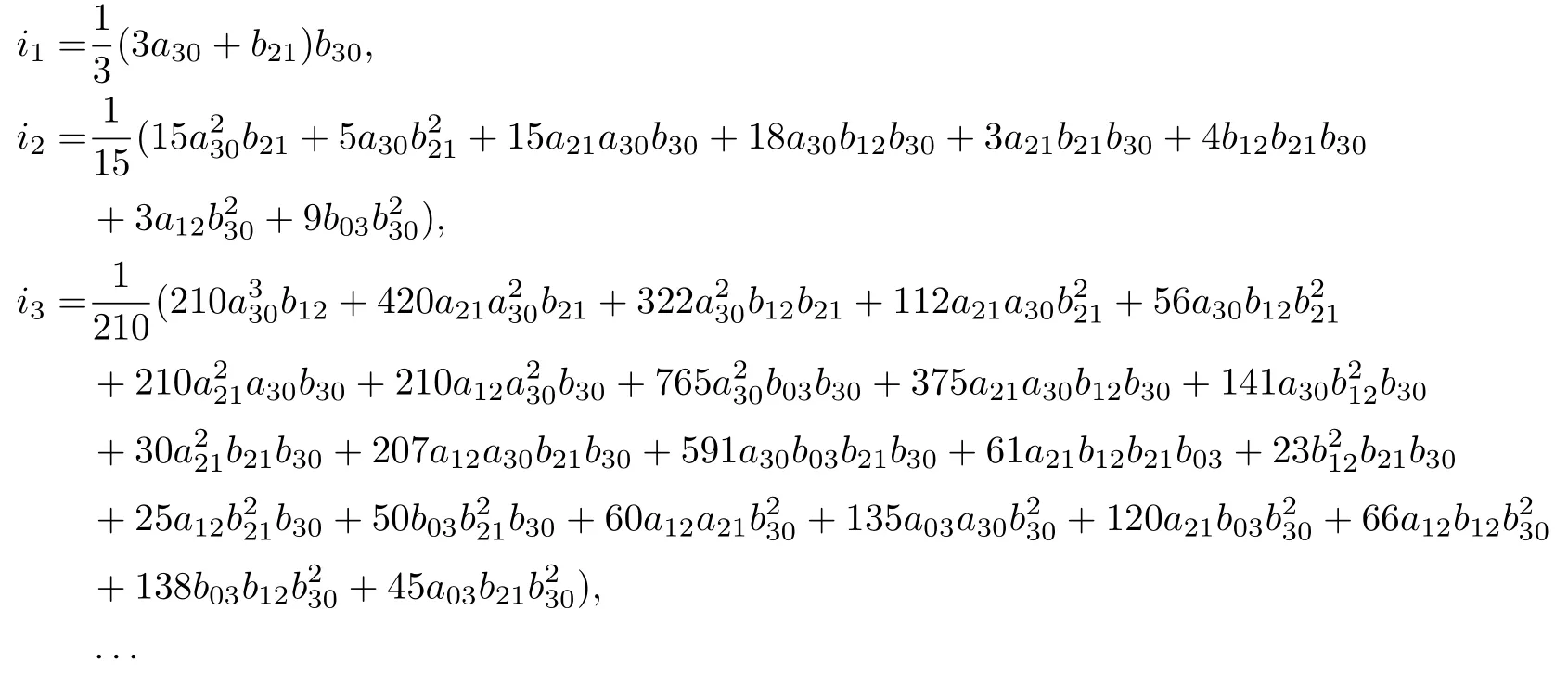
這樣, 得到了系統(tǒng)(19)可積的一個必要條件為

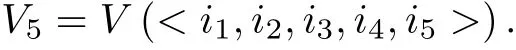
利用minAssGTZ 程序?qū)5進(jìn)行不可約分解, 得到了2 個不可約集, 分別滿足C1和C2的解集,仍記為C1和C2. 因此,C1∪C2=V5?V. 必要性得證.

為了證明充分性, 即V5?V, 需要證明C1?V且C2?V.

C1: 若b30=0, 則a30=b21=0, 此時系統(tǒng)(19)顯然可積.

當(dāng)b30/=0 時, 有

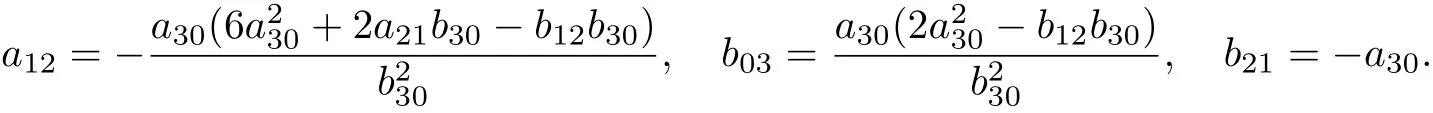
因此, 系統(tǒng)(19)可化為

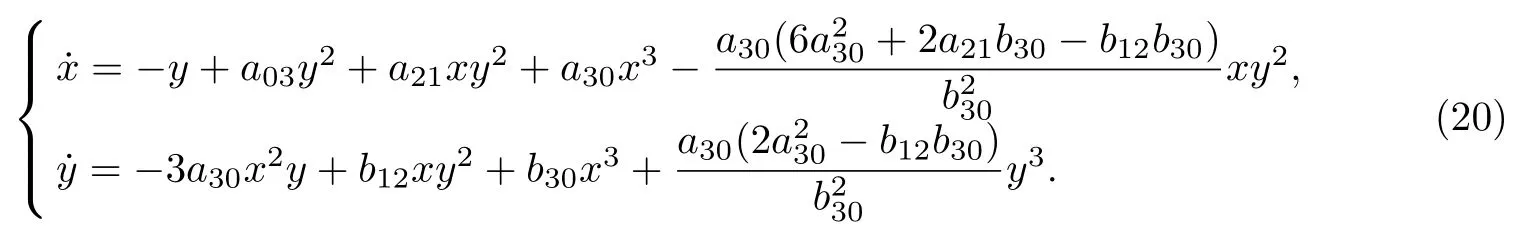
計算可得, 系統(tǒng)(20)有Darboux 因子

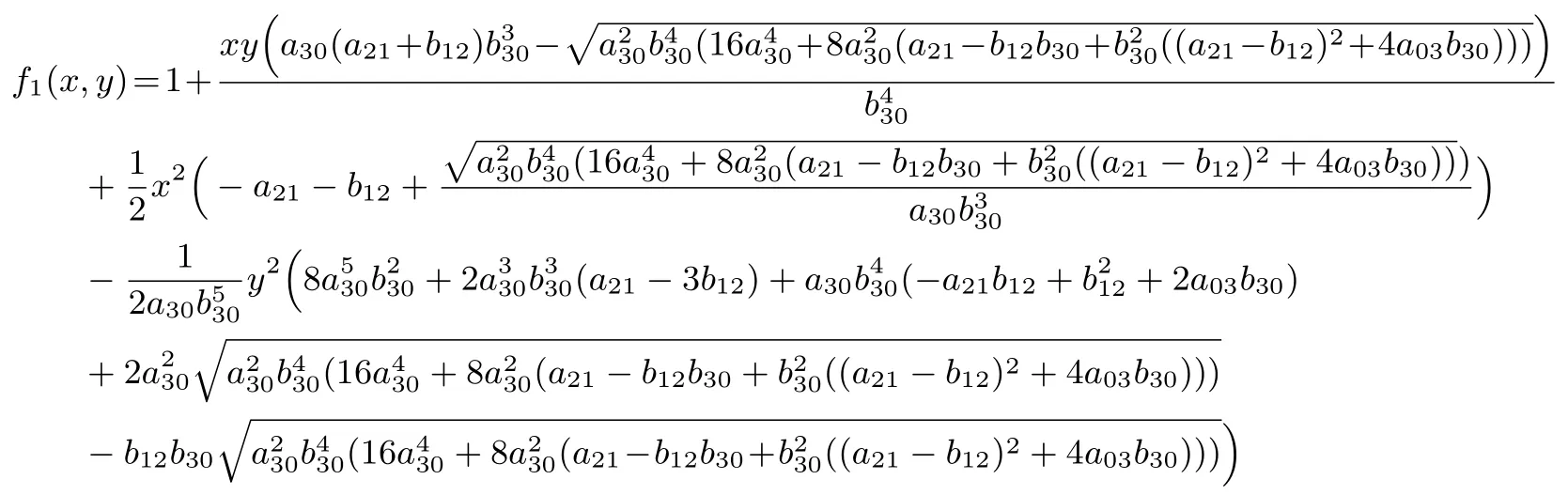
和

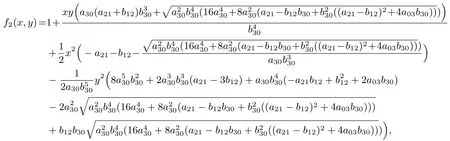
并且對應(yīng)的余因式分別為

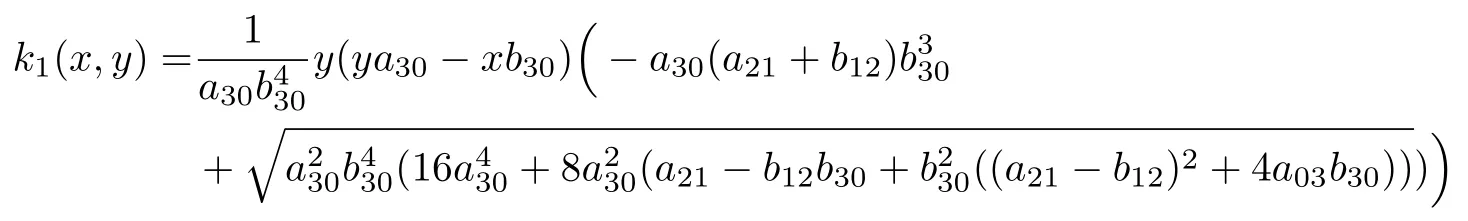
和

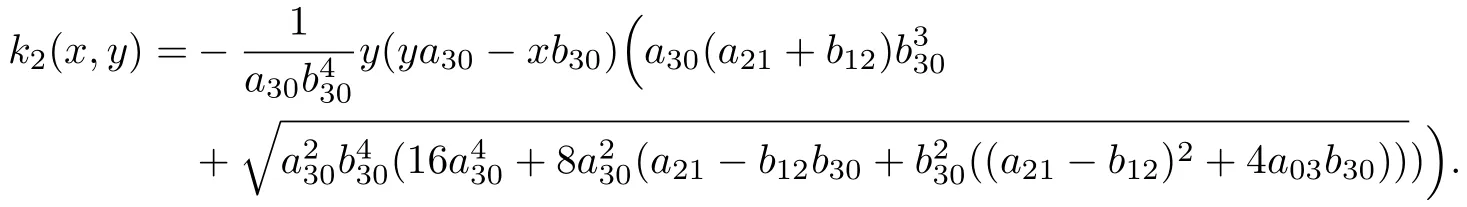
而系統(tǒng)(20)的發(fā)散量為

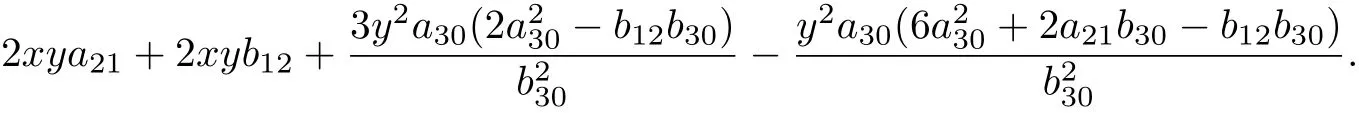
由定理1, 得到積分因子

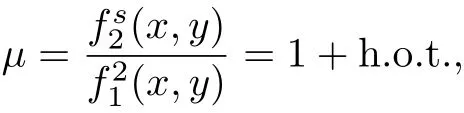
其中,

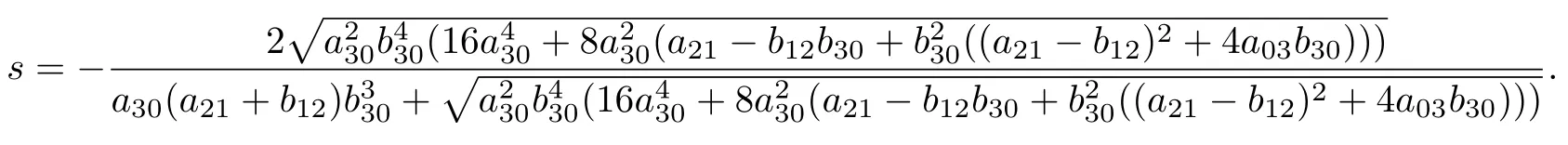
由定理1 可知, 系統(tǒng)(20)可積.

C2: 此時系統(tǒng)(19)為哈密頓系統(tǒng), 顯然可積.

最后, 考慮系統(tǒng)(19)在可積條件下冪零奇點(0,0)的分類情況. 條件C2下系統(tǒng)為哈密頓系統(tǒng), 具體的分類結(jié)果已在文獻(xiàn)[15]中給出. 而條件C1下有如下的結(jié)果.

定理9對于滿足條件C1的系統(tǒng)(19), 當(dāng)b30＞0 時, 原點為1 階冪零中心; 當(dāng)b30＜0 時,原點為1 階冪零鞍點; 當(dāng)b30=0時, 原點為非孤立奇點

證明 由定理8 可知, 當(dāng)b30/=0 時系統(tǒng)(20)有積分因子

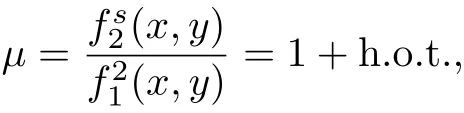
對應(yīng)的哈密頓函數(shù)非常復(fù)雜, 但可以得到其泰勒展開式的前若干項:

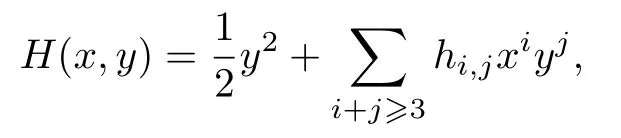
其中,

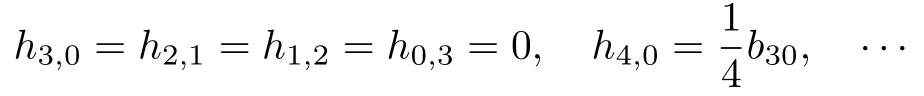
因此, 當(dāng)b30＞0 時,h2=h3= 0,h4＞0, 原點為1 階冪零中心; 當(dāng)b30＜0 時,h2=h3=0,h4＜0, 原點為1 階冪零鞍點; 當(dāng)b30=0 時,a30=b21=0, 則直線y=0 上所有的點均為奇點, 即原點為非孤立奇點.