透析教材 探究結(jié)論
———橢圓定義的思考

◇ 江蘇 翟美華

在教材中橢圓的定義：平面內(nèi)到兩個(gè)定點(diǎn)的距離之和為定值(該定值大于兩個(gè)定點(diǎn)間的距離)的點(diǎn)的軌跡．在某些例題或習(xí)題中,給出動(dòng)點(diǎn)滿足的條件,求解后發(fā)現(xiàn)其軌跡為橢圓或橢圓的一部分,這些動(dòng)點(diǎn)滿足的條件成為橢圓定義的重要補(bǔ)充形式,應(yīng)用這些定義形式往往能實(shí)現(xiàn)問題的簡捷處理．

1 伸縮定義

課本練習(xí)若M為圓x2＋y2＝4上任意一點(diǎn),作MD⊥x軸于點(diǎn)D．在M運(yùn)動(dòng)時(shí),求MD的中點(diǎn)P的軌跡方程．

例1F1,F2是橢圓的兩焦點(diǎn),點(diǎn)P(x0,y0)為橢圓C內(nèi)部一點(diǎn),判斷直線y0y＝1與橢圓C的交點(diǎn)個(gè)數(shù)．

解析

2 斜率定義

課本練習(xí)設(shè)A(－5,0),B(5,0),直線PA,PB交于點(diǎn)P,且,求點(diǎn)P的軌跡方程．

例2如圖1,M,N分別是橢圓的頂點(diǎn),直線y＝kx(k＞0)交橢圓于點(diǎn)P,A,且P在第一象限,PC⊥x軸于點(diǎn)C,直線AC交橢圓于點(diǎn)B．證明：PA⊥PB．

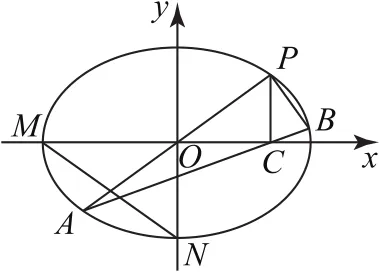
圖1

解析

設(shè)P(x1,y1),B(x0,y0),則A(－x1,－y1),C(x1,0),

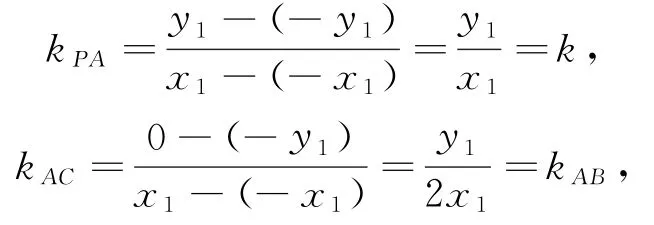
3 距離比定義

課本練習(xí)點(diǎn)P(x,y)到F(4,0)的距離與其到的距離之比為,求P的軌跡方程．

例3圓C1：x2＋y2＝100,C2：x2＋y2＝16,A(－4,0),B(4,0),離心率的橢圓C過點(diǎn)A,B,且一條準(zhǔn)線l與C1相切,求橢圓C與l對(duì)應(yīng)的焦點(diǎn)F的軌跡方程．

解析

如圖2,設(shè)F(x,y),過A,B,O分別作準(zhǔn)線l的垂線,垂足分別為A1,B1,O1,由平面幾何性質(zhì)可得|BB1|),|AA1|＋|BB1|＝2|OO1|＝2×10＝20．由橢圓的距離比定義可知,則|AF|＋|BF|＝10＞|AB|＝8,則點(diǎn)F的軌跡是橢圓,其軌跡方程為

圖2