New method for rekindling the explosive waves in Maxwellian space plasmas

G C DAS

Kalikadas Road Byelane, Hazrapara, Coochbehar-736101, West Bengal, India

Abstract

Keywords: Maxwellian complex plasma, nonlinear waves, soliton and shock propagation, (G′/G)method, space plasmas

1.Introduction

Studies on nonlinear waves have highlighted many milestones such as heuristic features in laboratory and space plasmas.Consequently, considerable interest has spurred many researchers to examine the formation of chaos, turbulences, various natures on solitons [1, 2] and worked on theory, experiments and satellite observations on space plasmas.Finally, nonlinear acoustic modes, augmented through the derivation of the Korteweg-de Vries (KdV) [1] equation and Sagdeev potential equation[2],are a pioneering platform leading to finding nonlinear acoustic waves as solitons of different kinds, including shock waves [3].During the last several years, there has been increasing interest on soliton dynamics in various plasmas with the view of having applications towards the experimental set up [4] and satellite observations on ionospheres [5, 6].It has provided a solid basis to bridge theories, experiments and satellite observations of various plasma environments in planetary rings[7,8],cometary tails [9, 10], Earth’s magnetosphere [11], and Earth’s auroral ionosphere [12].Despite the literature survey showing numerous studies on soliton dynamics theoretically and in experiments, there are inadequate observations of space plasmas, drawing much more attention to the expeditious study of the nonlinear acoustic mode.Consequently,studies have been extended to the dust acoustic wave(DAW)[10, 13-15],which plays a decisive role in different domains of space plasmas; soon after it was realized that the observations,without the dust constituents,might be missing many salient features of DAWs.It is hoped this study will be be useful to understanding the dynamical behaviors of nonlinear waves,out of which,plasma with dust charges is expected to be a new class of nonlinear waves in plasmas.It has been thought further that planets and stars could be formed from the dust clustering of nebulae commonly found in polluted astroplasmas around Saturn’s rings,planetary rings[7,8],etc,and this deserves study in astroplasmas[16,17],in addition to over the surfaces of moons and asteroids [18, 19].Another type of acoustic mode,electron-acoustic waves(EAWs),have been studied in parallel in multicomponent plasma, whose constituents are hot electrons and cold electrons.It has been seen that nonlinear features greatly elucidate the broadband electrostatic noise (BEN) observed in the Earth’s and planetary magnetosphere [20].Subsequently, the generation mechanism of large-amplitude electrostatic solitary waves has been found in various astroplasmas [21-23], where electrons may be trapped, and form a series of isolated electron holes through the coalescence of trapping potentials.The mechanism on the evolution of solitons have the merit to study the nonlinear wave dynamics in multi-temperature electron plasmas.Since the inception on nonlinear waves, several heuristic milestones have been executed in nonlinear acoustic modes along with the formation of double layers, different natures of solitons and electron holes in spaces [24-27].Actually the large-amplitude narrow wave packet with the generation of high-energy traps the electrons and nonlinear acoustic modes deriving the electron-acoustic waves in a way which correlates exactly with the works of Omura et al[21, 22] and Abid et al [28].One expects always a dominant mode with the generation of high-energy narrow wave packets, and it exhibits the explosions relying on similar occurrences in astroplasmas.Moreover, study on solitary waves has the same mechanisms to describe the electronacoustic waves,which were observed first by the Fast Auroral Snapshot (FAST) spacecraft [29] and later by the Polar spacecraft [30].Overall, studies have been motivated to find the various solitons, double layers, shock waves, electronacoustic waves augmented through the derivation of nonlinear wave dynamics in space plasmas over Mercury,asteroids and comets, as well as on moons’ surfaces [24].Again the shock waves in plasmas, causes by the fluctuation of dust charging,Landau damping, particle reflection on dust grains, have received considerable interest in recent years [31, 32].Because of the polluted massive dust grains in plasmas,observations are inadequate to know the dynamical behaviors of nonlinear waves in astroplasmas centered around their occurrences over cometary tails, interstellar and circumstellar clouds,asteroid zones[33-38],etc.As a whole,the nature of electrostatic waves has been studied, including solitary waves, DAWs, shock waves [39], the physics of double layers and their role in astrophysics [6], as well as the formation of dust atmosphere over moons’ surfaces[18,19,40,41],followed by the experiments on dust acoustic shock waves [42-44].Observations have spurred the scientific community to realize that for astroplasmas, one should take a proper account of dust grains; otherwise observations might be erroneous.Studies have then given new threshold areas on the ambiguous nature of dust grains in forming the stable dust clouds, which were earlier thought to be pristine space environments commonly found in the Milky Way and Saturn’s rings [18, 45-47].This has led to serious implications in plasmas generated from the discovery of fine structure of Saturn’s rings by the Voyager spacecraft [11, 33, 34] and the output has been applied to interpret low-frequency noise enhancement by Vega and Giotto space probes in the regions of Halley’s comet.Perhaps nonlinear waves have the boldest applications to be seen in astroplasma environments [48, 49]viz.understanding the Great Red Spot (GRS) features in the Jovian atmosphere and crystallization of the dust grains as the basis of nebulae formation, intensifying research interest in exploring the essential ingredients for the formation of stars and planets.There are many reasonably countable works which exhibited different kinds of nonlinear waves and deserve credit, but we are reluctant to cite them all here.The present study on acoustic modes in Maxwellian dusty plasmas expects new features,such as the progenitor of various shock wave formation and soliton propagation.Our interest has then expanded enormously to study the Burgers and KdV-Burgers equations in Maxwellian complex plasma with the effect of dust charge fluctuations.We first focused our attention to outline the formation of shock wave propagation along with the generation of high-energy electrons charging the neutral particles and explained that the explosions or collapses in solitons,of late,has recently shown soliton radiation[50-52].Further credit goes to the observations of Gao and Tian [53],who made significant observations on the formation of nebulae in atmosphere or exosphere.All the observations revealed that the nonlinear waves could have the threshold applications in many interstellar spaces [54-56], in Earth’s auroral regions and magnetosphere [47, 55], asteroids [57]and at the progenitor of Saturn’s spokes [23, 24].

To find out an exact and accurate wave solution of the nonlinear wave equation, we adopt a new method, known as the (G′/G) method [58], to yield the existences and propagation of shock waves and robust solitons.During the last several decades, researchers have dedicatedly used many powerful methods such as the Lie group method [59], Sine-Gordon method [60], B?cklund transformation [61], and the Tanh method[62,63]to find the salient features of nonlinear wave dynamics in plasmas.Among all, the (G′/G) method has shown very good success by Huibin and Kelin [64] and later by Wang et al [58] to evaluate the exact solution of nonlinear wave propagation.In fact, being concise and straightforward, the (G′/G) method has been applied to handle the nonlinear wave equations in a direct manner with no requirement for initial or boundary conditions.Recently Das and Sarma [32] customized the technique for the KdV equation and the authors recognized its success in solving for the soliton dynamics thoroughly in astroplasmas; this might be an advanced knowledge yet to be explored expeditiously.

Based on all the observations, this paper has been structured to study the nonlinear wave dynamics in a Maxwellian plasma contaminated with the dust charge fluctuations, and descriptions are discussed in section 1.Section 2 deals with the basic equations governing the plasma dynamics.Section 3 reviews the derivation of the Burgers equation and thereafter (G′/G) method is used to yield the properties of nonlinear waves.Results are discussed graphically (in section 4) with the thoughtful choice of typical plasma parameters from different space plasma environments,exactly what has been found in cosmic dusty plasma laden in the ionospheric auroral region, radial spokes of Saturn’s rings,planetary nebulae and the solar F-corona region.Section 5 deals with the solution of the KdV-Burgers equation followed by the nascent shock wave propagation as the precursor of soliton dynamics.Section 6 highlights the salient features of wave propagation with the hope of having potentiality for other plasma environments.Finally, section 7 analyzes the overall results and conclusions.

2.Basic equations and mathematical formalism on nonlinear waves

We have considered a simple unmagnetized Maxwellian plasma constituents with electrons (subscript e) and ions(subscript i) contaminated with the negatively charged dust grain (subscript d) under the influence of dust charge fluctuations.Here nonlinear acoustic wave propagation has been taken unidirectional (along x direction), and the basic equations governing the plasma dynamics, following Asgari et al [65], Das et al [66], are written in normalized form as follows.

Equation of continuity:

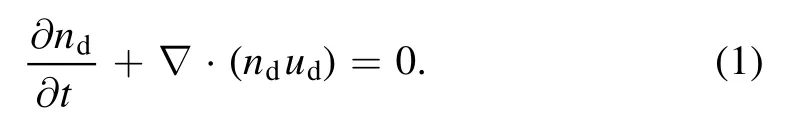
Equation of motion:

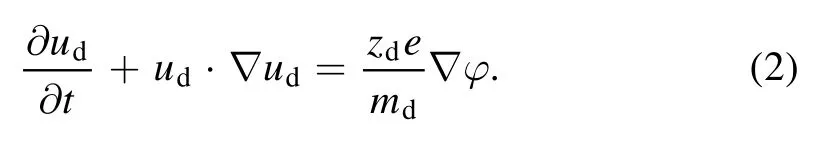
Supplemented by the Poisson equation given by

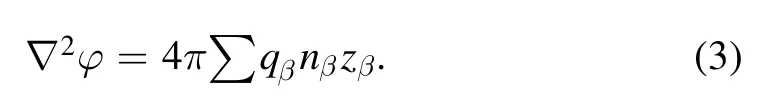
Hereβ(=i, e, d) stands respectively for the ions,electrons and dust particles.mdis the mass of the dust particle moving with speed,udnormalized by ci=(κBTe0/mi)1/2(κBis the Boltzmann constant) and nβis the charge number density normalized by its equilibrium value nβ0, where suffix ‘0’ represents the parameters at equilibrium state.The ion and dust charge numbers are given byzi,d,where zdis the number of electrons residing on dust grain surface.φis the electrostatic potential normalized by(κBTe0/e).The time and space variables t and x are normalized respectively byandAll other symbols have their usual meanings defined elsewhere [32].The plasma parameters are now perturbed aswhereβf0is the plasma parameters at equilibrium andis its perturbed quantity.Based on the assumptions that electrons and ions are Maxwellian,the Poisson equation[equation(3)]can be written as follows:

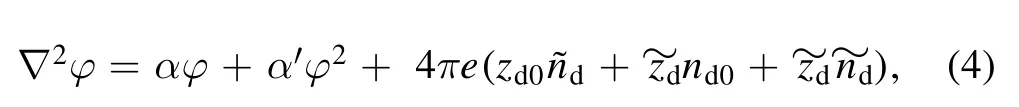
where

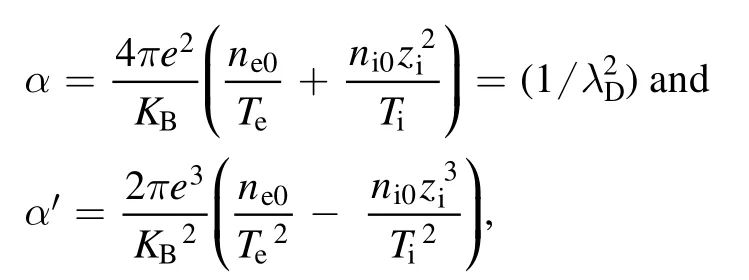
whereTi,eare the temperatures of ions and electrons.

Dust grains are continuously being charged by generating electron and ion currents and followed the charging equation as

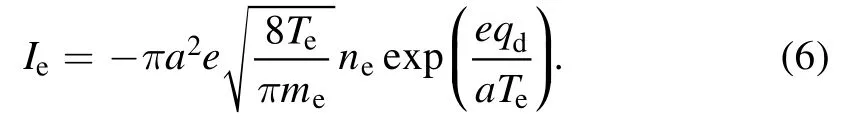
Now, following Das et al [66] and Jana et al [67],charging equation has been simplified as

where

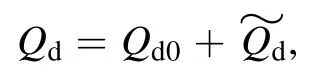
whereCis the capacitance of the dust grains,ω0=kBTi?eφf(shuō)0andφf(shuō)0is the equilibrium floating potential.Using equations (8) in (7), we get

with

and

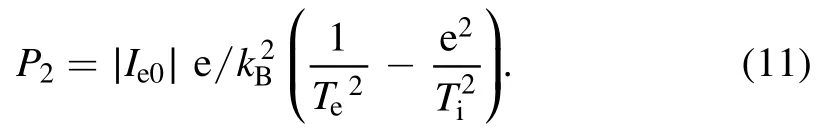
Initial floating dust potential can be obtained from the stability of dust charging condition, i.e.

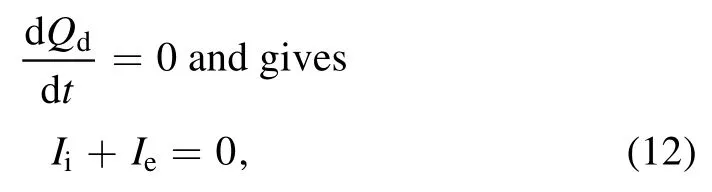
which depends on the potential variation and temperatures of the plasma.Thus the charging equation has to solve for dust potential with the variation of plasma potential.

3.Derivation of Burgers equation and use of the(G′/G) method

To study the natures of the soliton propagation, we,following Washimi and Tanuiti [1], employ the reductive perturbation technique to the basic equations.The space and time coordinates are stretched through the following relations

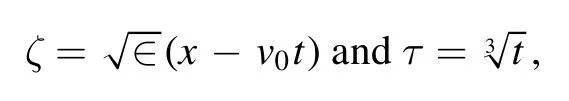
where∈is the expansion parameter characterizing the strength of the nonlinearity in the dynamics and v0is the initial phase velocity of the acoustic mode and will be evaluated later in a self-consistent manner.The plasma parameters are now expanded with usual perturbation scheme as

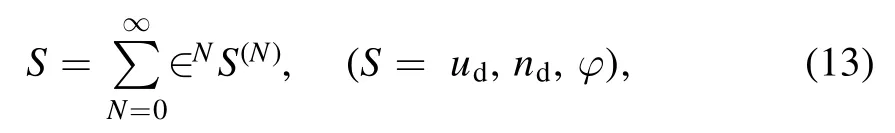
whereS(0)=0forφandud.

Now, using the stretching coordinates and reductive perturbation technique to the basic equations, we derived,from the balance of first-order terms in∈, the following relations:

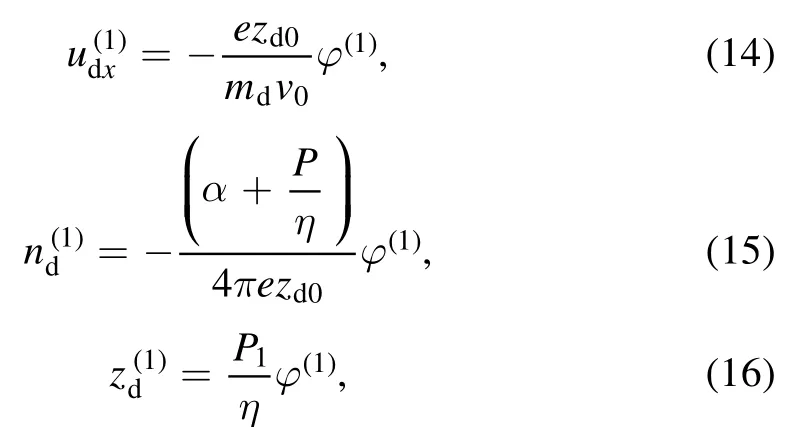
from which the phase velocity,v0, derives as

whereωpdis the dust charge frequency defined as

and

Next,the higher order in∈yields the following relations:

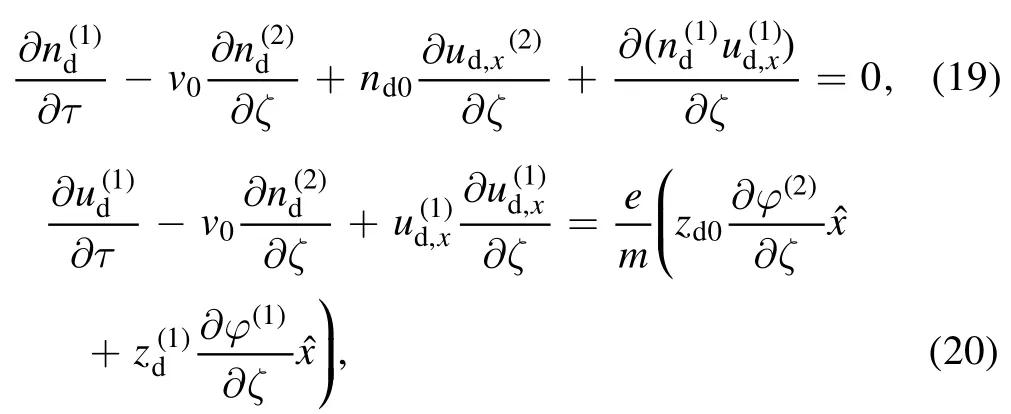
After some mathematical simplifications of equations (19)-(22), along with the first-order results, the elimination ofderives the desired Burgers equation as

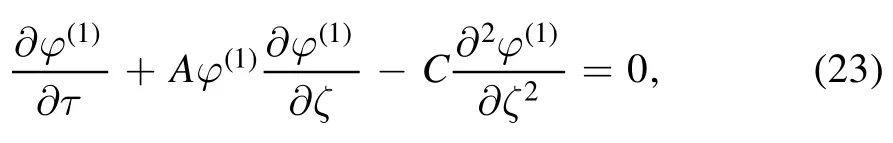
with

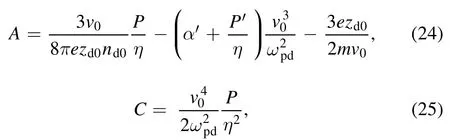
It is well known that the solution of Burgers equation results in the shock wave propagation.Apart from the existing methods, a new method, known as (G′/G) method, has been exercised to find out an exact and accurate wave solution of the nonlinear wave equation and its propagation.We then attempt to execute the technique to solve the nonlinear wave equation for studying the nonlinear behaviors of Burgers equation, which might be useful for enhancing our understanding of new findings in space plasmas.Now, in order to use the (G′/G) method, we employ the transformationwithξ=k(ζτ?V) (where k?1is the normalized space width of the nonlinear wave propagation with respect to a frame moving with the velocity V) along with the following boundary conditions

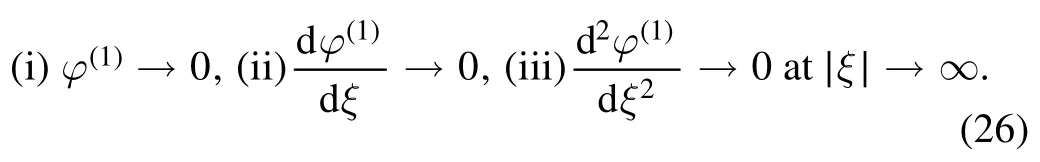
Then the Burgers equation reads, after integrating once(following Das and Sarma [32]), as

where M is the constant of integration.

Now to get the shock wave solution of equation(23),the(G′/G) method needs to assume a series solution for ()ψ ξas

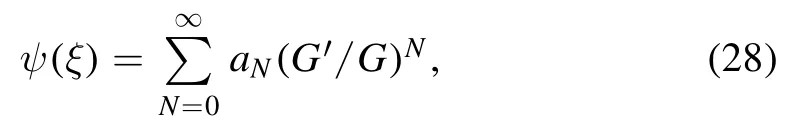
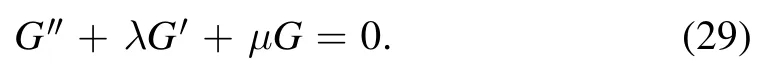
Now substituting the series (28) in equation (27), we obtain the recurrence relation as

Thence the actual terms in the seriesψ(ξ) has to be determined.For the sake of mathematical simplicity and,without loss of generality, we adopt a simplified series,truncating it into a finite length with N+1 terms.Thereafter the number of terms has been derived by equating the highest power of linear terms with that of the nonlinear terms.Now the process evaluates the exact number N of the series as N=1 and correspondingly the series becomes

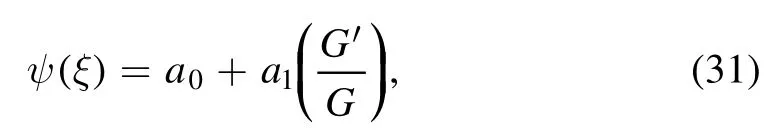
from which, we get

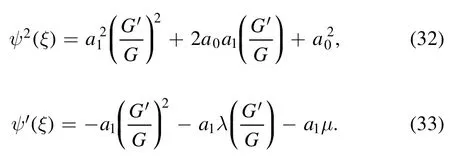
Now the expression forψ2(ξ)andψ′(ξ)are substituted in equation(27)and we then,equating the coefficients ofderived the following equations:

From the above,by using Mathematica-10,the following parameters are found:

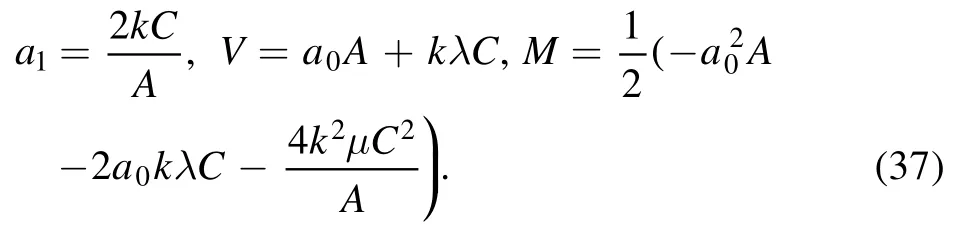
Finally, solution (31), after using (37), reduces as

Now the solutions of the Burgers equation(equation (23)) as of equation (38) depends on M derivable from equation (27) and G needs the solution of equation (29) as

The nature of solution depends fully on the discriminantλ2?4μ.Consequently the following cases arise.

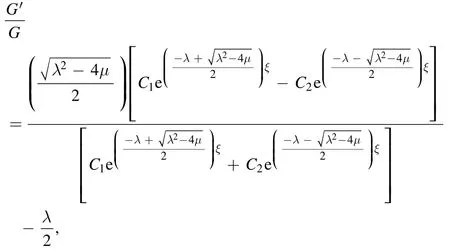
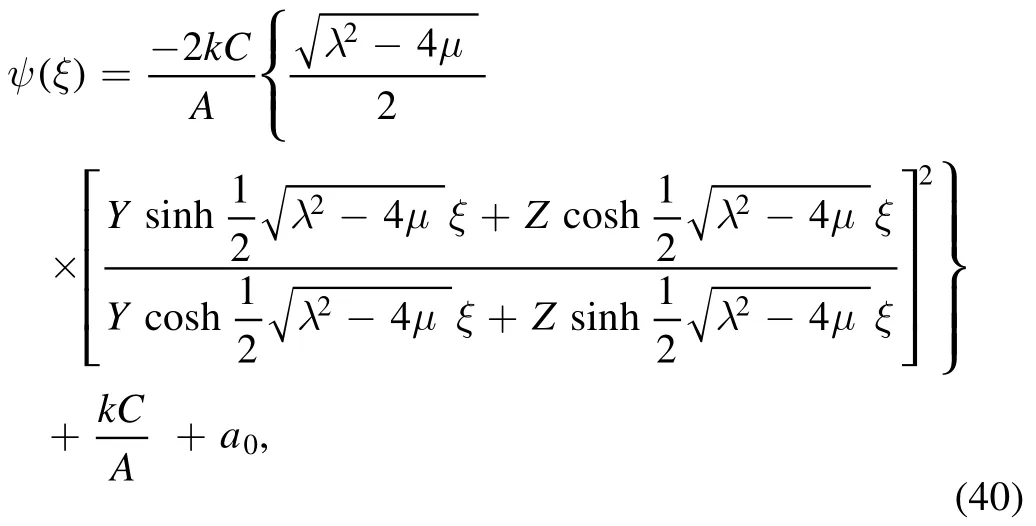
which, as the particular case withμ=≠Y0,0,reduces as

Solution (41) represents the shock wave propagation in Maxwellian dusty plasma and depends fully on the strength of the nonlinearity, which varies with the plasma parameters.We note that dust charge fluctuation has a dissipative nature,which yields shock wave propagation even though the original model does not have any dissipation.k?1is the normalized width of the wave propagation derived in a frame moving with the velocity, V, and the amplitude of the shock wave (Φm) varies inversely with the nonlinear effect, A.However, the recovery of the shock wave solution from the Burgers equation signifies the successful utility of the proposed mathematical approach to the Burgers equation.Nevertheless, the novelty of the present approach reflects its simplicity over the conventional approaches and might trigger curiosity to use this with different nonlinear wave dynamics.

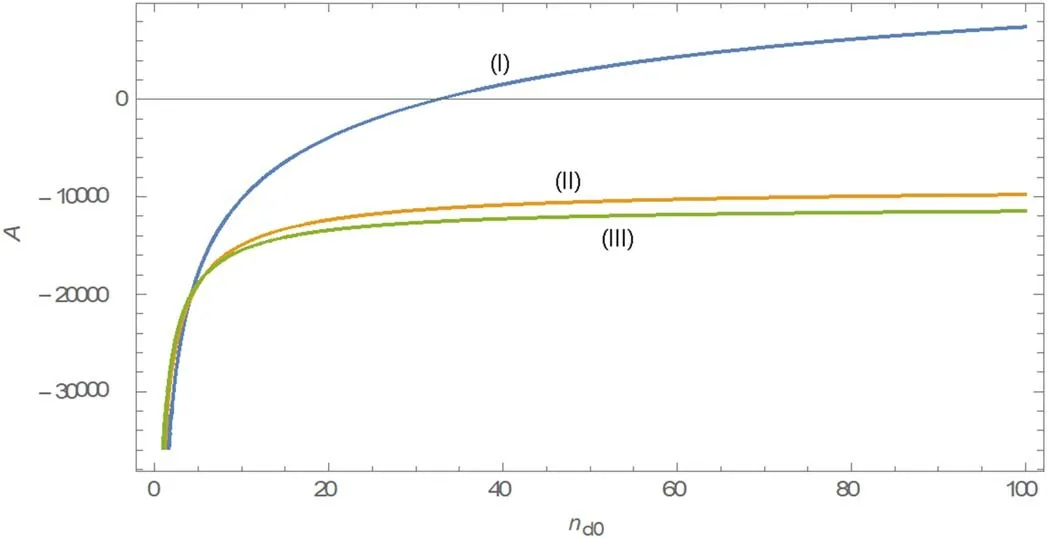
Figure 1.Variation of A with nd0 in the ionospheric auroral region with ion temperatures (I) Ti=2×102 K, (II) Ti=4×102 K,(III) Ti=5×102 K and electron temperature Te=104 K.

Again, forλ2?4μ＜0,we have the solution

and the solution, forλ2?4μ=0,derives as

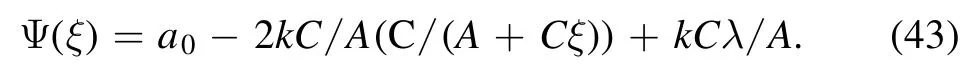
Both the solutions of the Burgers equation are simple wave solutions.But our interest has to focus only on the shock wave in isolation, and thus we do not undertake discussions on it.

4.Results on graphical discussions

We have studied the evolution and propagation of the Burgers shock wave in a Maxwellian plasma contaminated by the fluctuations of dust-charged grains which is providing a dissipation-like effect on the formation of shock wave.To understand the nature of the shock wave, we have chosen plasma regions from the ionospheric auroral region with some empirical values as of ion temperatures (I) Ti=2×102K (line I), (II) Ti=4×102K (line II) and (III)Ti=5×102K(line III)along with the electron temperature Te=104K and plotted(figure 1)the A variation with the dust density.

Figure 1 shows a distinct polarization by the changes in A due to the variation of the dissipative-like effect and ion temperatures.For low ion temperatures (I) Ti=2×102K(line (I)), a variation of A yields negative values when dust charging is less and becomes positive with the increase of dust charging effect in the plasma.However, the negative profile of the shock wave will be widened with the increase of ion temperatures, displaying a rarefactive shock wave, and a compressive wave is not exhibited therein.The totality of the observations on shock wave solutions depicts different profiles bifurcated by a critical dust density at which A=0.Consecutively,the wave grows very large with the generation of high energy with the formation of small region of shock wave propagation and is prone to having an explosive nature.Again, for high temperatures (lines II and III), A remains always negative, the charging effect does not play any effective role in changing the natures of waves as of line I and the wave does not grow to take on an explosive nature.

We again consider another plasma model, which can be found in the formation of spokes in Saturn’s rings, with ion temperatures (I) Ti=1×102K, (II) Ti=2×102K, (III)Ti=4×102K and electron temperature Te=2×104K(plotted in figure 2).

Figure 2 exhibits reverse polarity in shock modes which are quite different from the natures found in the ionospheric auroral region.Here A changes from negative to positive with the increase of ion temperatures.Variation of A for higher ion temperatures (II) Ti=2×102K (line (II)) and (III)Ti=4×102K(line(III))yields a negative value(in the case of low dust density)and exhibits altogether new observations at the changes of the polarity in A.It can be easily seen that the amplitude of the acoustic wave grows very large as and when the nonlinear effect diminishes to zero.Actually such large-amplitude wave structures have a similar nature in the auroral region observed by the FAST and POLAR satellites.The interpretation of the nonlinear waves draws more attention because of their significant roles in the auroral region and in ionosphere-magnetosphere interactions.Moreover,there is a chain process in generating the high-energy electrons to charge up the neutral or dust particles to a stage of having an explosive wave, which is specifically caused by the interaction of dust charge fluctuations and temperatures.Similar phenomena have been seen in the ionospheric auroral region with ion temperatures Ti=2×102K (line (I))resulting in the source of radiation-like phenomena resembling the observations at the solar flares [11, 29].Again the shock wave region, i.e.the region of high-amplitude wave with the negative polarity,is widened with the decrease of ion temperatures and reflects the non-existences of compressive waves, which is quite opposite that observed in the ionospheric auroral plasma region.For further support, we have taken another plasma model from the solar F-corona with ion temperatures (I) Ti=2×104K (II), Ti=4×104K, (III)Ti=8×104K and electron temperature Te=8×105K(plotted in figure 3).

Figure 2.Variation of A with nd0 in radial spokes of Saturn’s ring region with ion temperatures (I) Ti=1×102 K, (II) Ti=2×102 K,(III) Ti=4×102 K and electron temperature Te=2×104 K.

Figure 3.Variation of A with nd0 in the solar F-corona region with ion temperatures Ti=2×104 K,(II)Ti=4×104 K,(III)Ti=8×104 K and electron temperature Te=8×105 K.

Figure 3 shows the shock wave in the solar F-corona region having a similar nature as that of congruent character in radial spokes of Saturn’s rings; i.e.with an increase in ion temperatures, the value of A becomes large and shows a rarefactive shock wave with negative polarity.Overall results,from the first two figures, yield a critical density around which the nonlinear effect tends to zero,due to which there is a growth of high energy in the shock wave.Moreover, in the case of a strongly coupled dusty plasma, the dissipation-like effect is present due to the strong correlation with the dust charge fluctuations.This can be understood from the fact that the viscous effect could not be the only reason to form the shock wave in plasmas;rather the dust charge fluctuations can also produce the shock wave propagation.We see again that the dissipation has been provided by the strong correlation among the dust charge fluctuations and temperatures in space plasma around which the shock front dissipates.We observe that with the increase of dust density, a transition of shock front occurs from the negative polarity to positive polarity(figures 1 and 2)and exhibits the propagation of compressive and rarefactive waves,whereas figure 3 shows the rarefactive shock waves in the plasma region of solar F-corona.

5.Use of (G′/G) method to KdV-Burgers equation

To study further the nonlinear wave phenomena, we, following an earlier work [67] and equation (23), derive the KdV-Burgers equation in the complex Maxwellian plasma under the influence of dust charge fluctuations as

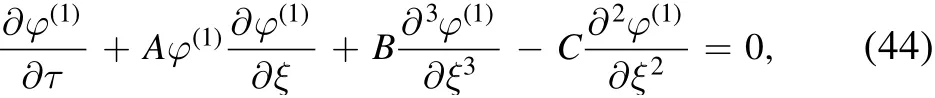
with

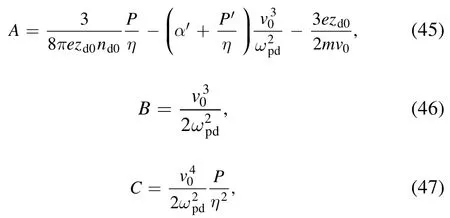
As before, in order to use the (G′/G) method, we employ the transformationwithξ=k(ζτ?V)(with respect to a frame moving with the velocityValong with the boundary conditions (26)) to the KdV-Burgers equation.

Further, to get the solution of equation (44), (G′/G)method needs to assume a series of solution as

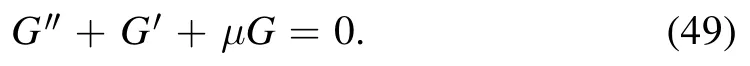
with the general solution as

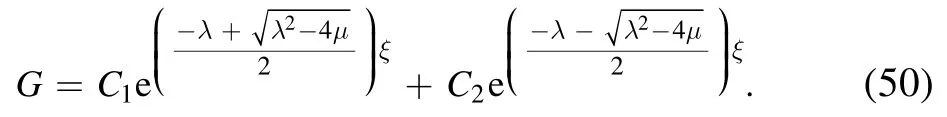
As before,the exact number N of the series(48)has been truncated, with the usual catchy way, as N=2.Correspondingly, the series becomes

Now the use of equations(48)-(51)and then equating the constant term,we get the following equations:

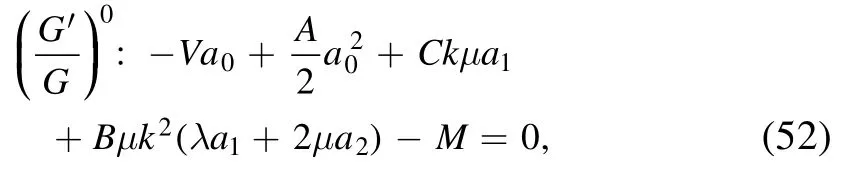
Equations are then solved by Mathematica-10 which enables us to derive the following:

where

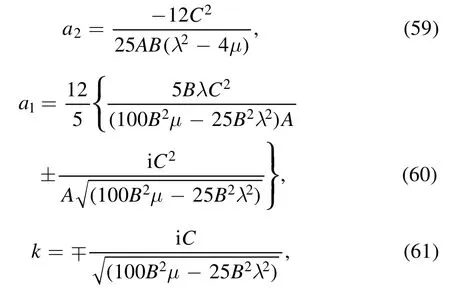
which, forλ2?4μ＞0,derives the solution as

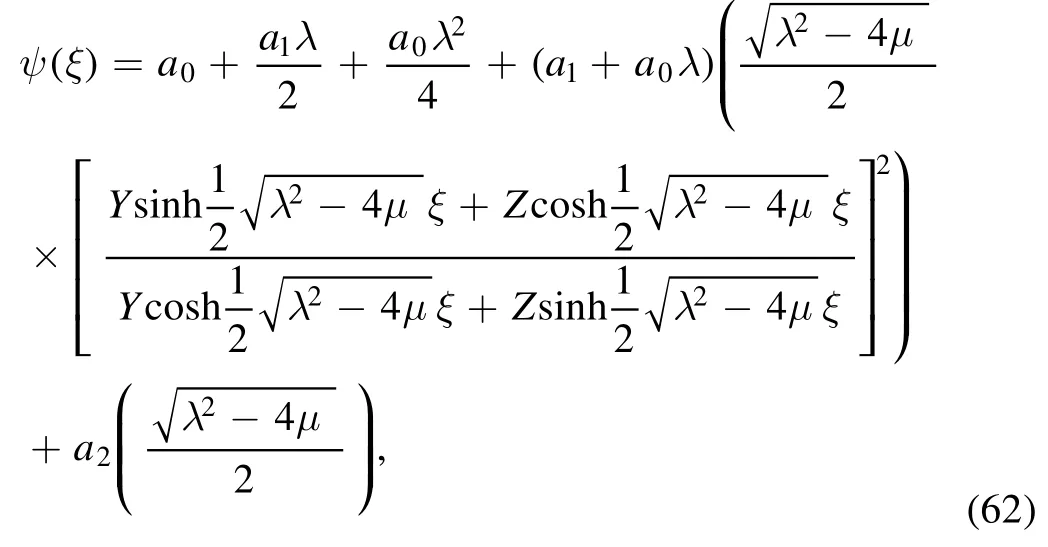
and,as similar to the earlier particular case with μ=0,Y ≠0,Y2＞Z2and λ＞0, derives the solution as

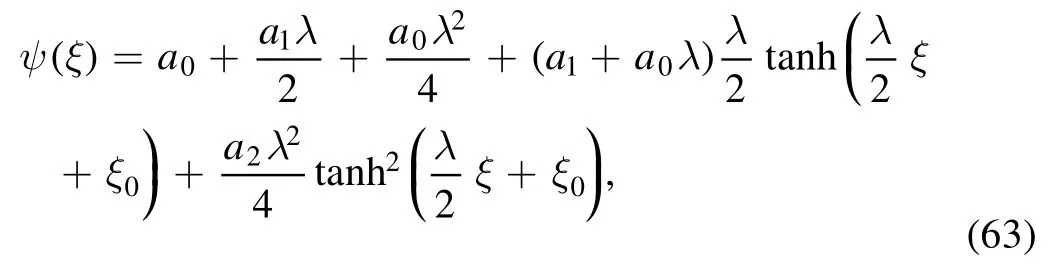
The solution has then been simplified further as

whereV,a2,a1,kare the functions of plasma constituents anda0is constant.

6.Results and discussions

Solution (64) exhibits the desired shock wave propagation coexisting with the soliton propagation in a plasma contaminated by the fluctuations of dust-charged grains and relaying their existences in various astroplasmas.The success of the (G′/G) method has shown in solving the nonlinear wave propagation resembling the superposition method applied to the KdV-Burgers equation[68].Here we observed that the solution of the KdV-Burgers equation exhibits a hump or well-shaped KdV solitary wave of sech nature as the precursor of the Burgers shock wave.We further noticed that a negative value of A occurs in the plasma region where the net dust charging is less due to which the acoustic mode yields a rarefactive soliton.But A becomes positive with the increase of the dust charging effect,and polarity occurs in the wave switching to the nature of compressive soliton propagation.Again, the solitary wave region is widened with the increase of ion temperature and consequently the compressive solitary wave does not exist.Thus the nature of the wave depends crucially on the dust charge fluctuations and temperature effect, revealing either a well-shaped soliton profile when A＜0 or a hump-shaped soliton profile when A＞0,leaving behind a critical density at which A=0 and the existence of solitary waves breaks down.In the neighborhood of critical density (i.e.at A →0), both the soliton and shock wave propagation grow to a high-amplitude narrow wave packet, and acoustic modes will collapse or explode depending fully on the conservation of energy in the wave packet.A similar transition on the shock front occurs,switching from negative to positive polarity and exhibiting the propagation of a rarefactive to the compressive explosive waves (discussed in figure 3).Again, electrons have the tendency to be trapped within the wave packet, generating high-energy electrons to charge the neutral particles, because of which, density depression occurs to exhibit the radiationlike phenomena.Moreover, the high-energy wave in the narrow wave packet is heading to blow up the pulses of the explosion or bursting waves, which very much resemble the phenomena of solar radio burst in spaces [69, 70].Our observations portray such occurrences in every region of the universe and might explain the inherent nature of similar phenomena in solar radio bursts as well as radiation in pulsar magnetosphere, termed as pulsar radiation [56, 71].

To support the observations, we have taken appropriate numeric data from the plasma regions of ionospheric auroral zones, Saturn’s rings, planetary nebulae and the solar F-corona.Figures 2 and 3 the display shock wave propagation superimposed by soliton propagation of different natures of rarefactive or compressive waves, depending fully on the variation of A.We have noticed that the wave yields the rarefactive soliton in the plasma region of a lesser dust charging effect, and then the wave, with the increase of charging effect (through the increase of nd0i.e.large amount of electrons are absorbed in charging the dust grain),displays the polarity to form compressive soliton propagation.These phenomena could be found in shock wave propagation as well.It is worth mentioning here that the soliton profile, a precursor to the double layers, will show the hump or wellshaped with the growth of a high-energy wave packet in solitons as well as in shock waves.Such characteristic phenomena of the solitary waves could have similar occurrences in electron-acoustic waves in multicomponent plasmas,coexisting with free and trapped electrons and new findings in various plasmas deserve credit [21, 22].Thus plasma configuration plays the crucial role in generating the high-energy wave packet with the occurrences of explosions, bursting or radiation in nonlinear waves in the universe and might explain the inherent nature of many nonlinear acoustic modes.

7.Conclusions

We have studied the evolution of solitons and shock wave propagation in simple Maxwellian plasmas under the influence of dust charge fluctuations.(G′/G) method has been used successfully to show the different nature of nonlinear waves in spaces.To support the observations, some typical plasma configurations from the auroral ionosphere, radial spokes of Saturn’s rings and from other astrophysical plasmas regions such as nebulae and solar F-corona have been chosen.It has shown that dust charge fluctuations are responsible for exhibiting the dissipation-like effect and that they exhibited a double polarity in a shock wave as well as in a solitary wave.First of all, it has shown the rarefactive shock wave is the forerunner, with rarefactive soliton propagation in plasma where dust charging is comparatively less.Thereafter, nonlinearity increases to be positive with the increase of dust charging, and because of which, the compressive nature of soliton and shock waves is exhibited.It has been shown that the nonlinear wave, in the neighborhood of the polarity region, has a tendency to grow low- and high-amplitude solitons and shock wave profiles, intensifying the growth of enormous electric pressure.Again, the high-energy electric field accelerates the electrons to charge up the neutral or dust particles to a stage of having high potential with high current energy that is also within a narrow wave packet.Such phenomena could be analogous,yielding the source of explosions and radiation on solitons and shock waves, which share a similar formation in solar radio burst in spaces.As a totality,the proposed (G′/G) method elegantly and convincingly solves the Burgers and KdV-Burgers wave equations to exhibit the shock waves superimposed by the solitons in the saucer of complex plasmas.Moreover it is worth mentioning here that the nonlinearity takes the dominant role of having a large-amplitude wave and traps substantial electrons within the narrow wave packet.

These trapping electrons form a series of isolated electron holes through the coalescence of trapping potentials and contributed high energy to the nonlinear waves, and then the nonlinear wave either explodes or collapses.Again the various nature of compressive and rarefactive nonlinear wave has been examined in the ionospheric auroral region and found to be quite different from that visited in the radial spokes of Saturn’s rings and solar F-corona regions.It has seen that the dust charge fluctuation is responsible for blowing up the pulses such as explosions or bursting waves, as well as radiation,resembling their occurrences in the solar radio burst III[27,69].Thus the nonlinear waves might be expected to be high-energy explosive waves,which might be the basis of the formation of stars, planets etc.Further observations revealed that the acoustic modes could be meandering the formation of soliton and shock waves given new findings, which might help to solve the uneven understanding between theory and satellite observations.Endeavors to study astrophysical interests and having more applicability headway to advanced knowledge for rekindling expeditiously in future.