Benchmark solutions of large-strain cavity contraction for deep tunnel convergence in geomaterials
Pin-Qiang Mo, Yong Fang, Hai-Sui Yu
a State Key Laboratory for Geomechanics and Deep Underground Engineering, School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou, 221116, China
b Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu, 610031, China
c School of Civil Engineering, University of Leeds, Leeds, LS2 9JT, UK
Abstract To provide precise prediction of tunnelling-induced deformation of the surrounding geomaterials, a framework for derivation of rigorous large-strain solutions of unified spherical and cylindrical cavity contraction is presented for description of confinement-convergence responses for deep tunnels in geomaterials.Considering the tunnelling-induced large deformation,logarithmic strains are adopted for cavity contraction analyses in linearly elastic, non-associated MohreCoulomb, and brittle HoekeBrown media. Compared with approximate solutions, the approximation error indicates the importance of release of small-strain restrictions for estimating tunnel convergence profiles, especially in terms of the scenarios with high stress condition and stiffness degradation under large deformation. The ground reaction curve is therefore predicted to describe the volume loss and stress relaxation around the tunnel walls. The stiffness of circular lining is calculated from the geometry and equivalent modulus of the supporting structure, and a lining installation factor is thus introduced to indicate the time of lining installation based on the prediction of spherical cavity contraction around the tunnel opening face. This study also provides a general approach for solutions using other sophisticated geomaterial models, and serves as benchmarks for analytical developments in consideration of nonlinear large-deformation behaviour and for numerical analyses of underground excavation.
2020 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Keywords:Convergence-confinement method (CCM)Cavity contraction analysis Tunnel convergence
1. Introduction
Tunnels improve connections and shorten lifelines (Kolymbas,2008), and large-scale tunnels are widely constructed for conveyance and storage (Zhou et al., 2014; Barla, 2016). Tunnel with a buried depth over 20 m or cover to diameter ratio over 5 can be treated as a typical deep tunnel(Peck,1969;Mair and Taylor,1993).Tunnel convergence is vital to the stability of underground excavation, as accurate control of tunnelling deformation is highly desired in geotechnical engineering, especially with the rapid development of urban underground traffic system. The convergence-confinement method (CCM), proposed in 1980s,aimed to provide analytical and graphical descriptions of the ground-support interaction of a deep circular tunnel within homogeneous and isotropic geomaterials, serving as a useful and effective method in the preliminary design stage for deep tunnel construction (Panet et al., 2001; Kainrath-Reumayer et al., 2009;Oreste, 2014). The concept of CCM lies on utilizing the arching effects of geomaterials and the adaptation of support measures to decisively absorb large deformation caused by excavation. The ground reaction curve (GRC) represents the pressure-deformation relation at the excavation surface, and the support characteristic curve(SCC)and the longitudinal deformation profile(LDP)indicate the retaining force/deformation and the installation time/location of the various support measures,respectively.The development of CCM is detailed in Oke et al. (2018).
Since the basic assumptions of CCM are consistent with those of conventional cavity contraction methods, the prediction of GRC is generally provided based on the cavity expansion/contraction theory (Carranza-Torres and Fairhurst, 2000; Vrakas and Anagnostou, 2014; Mo and Yu, 2017; Vrakas, 2017; Zou and Zou,2017; Yu et al., 2019). As the small-strain cavity expansion/contraction in elastic material (Timoshenko and Goodier, 1970)gains wide applications in various branches of science and engineering, analytical solutions have been extended to consider cohesive-frictional and softening behaviour of geomaterials, along with the assumptions of small-strains or a loosening factor for volumetric change(Yu and Houlsby,1995;Chen and Abousleiman,2013,2017;Zou and Xia,2017;Mo and Yu,2018;Chen et al.,2018;Zou et al.,2019;Li and Zou,2019;Li et al.,2019a,b).In respect of the circular openings in rock, semi-analytical solutions in nonlinear elasto-plastic materials were developed with some simplified hypotheses on boundary conditions and dispersal factors (Brown et al.,1983; Song et al., 2016). However, the tunnel long-term stability and its interactions with underground structures are determined by precise prediction of tunnelling-induced deformation of surrounding geomaterials. Theoretical analyses thus tend to remove any restrictive assumptions to provide reliable estimations during the design phase.
Small-strain assumption indicates the infinitesimal deformation,whereas the undeformed and deformed configurations cannot be distanced through the derived displacements that leads to the small-strain solutions approximate. Linearisation of small-strain assumption tends to remove the difference between Lagrangian and Eulerian descriptions,which is only valid for stiff materials;the method to simply transform the small-strain solution to largestrain solution is either empirical or semi-analytical with hypotheses (e.g. Vrakas, 2016). On the other hand, the large-strain assumption considers the nonlinear displacement gradient, and is exact for any deformation state, especially for materials with inherent nonlinearity.
This paper provides a framework for derivation of rigorous large-strain and quasi-static solutions of cavity contraction for prediction of confinement-convergence responses for deep tunnels in geomaterials. Considering the tunnelling-induced large deformation, logarithmic strains are adopted for both spherical and cylindrical cavity contraction analyses in linearly elastic, Mohre Coulomb and brittle HoekeBrown media. The fully rigorous solutions on GRC describe the volume loss and tunnel relaxation,while the ground-support interaction is obtained through incorporation of compression on lining structure for the SCC.The provided cavity contraction solutions could therefore serve as benchmark solutions for deep tunnel convergence in geomaterials,and contribute to the further developments on nonlinear and elasto-viscous analyses.
2. Cavity contraction problem and deep tunnel convergence
The problem in this paper considers a cylindrical or spherical cavity embedded in an infinite isotropic material with an initial hydrostatic stress condition0. The cavity pressurer;ais reduced from its initial value(equal to0)to cause contraction of cavity,and the cavity radius decreases froma0toa, as illustrated Fig. 1. The solutions are therefore developed to provide both evolutions and distributions of stresses and strains of the medium surrounding the cavity.
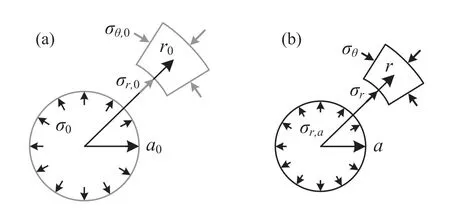
Fig.1. Schematic of cavity contraction for both cylindrical and spherical scenarios: (a)Initial cavity; and (b) Cavity after contraction.
Due to the axisymmetric configuration,the differential equation of quasi-static equilibrium can be expressed as

In continuum mechanics, analytical solutions are considerably simplified with assumption of infinitesimal strain, which are also termed as small-strain analyses.However,small-strain assumption in axisymmetric coordinates is restrictive and leads to no volumetric strain, whereas the deformation characteristics of geomaterials indicate finite strain,which requires equilibrium in every deformed state of a structure.
Therefore,to account for finite strain in geomaterials,the largestrain theory is adopted for derivation of rigorous cavity contraction solutions, and logarithmic strains (or Hencky strains) with no rotation are used in this study, i.e.

where εrand εare the radial and tangential strains, respectively;andr0is the original radius of an arbitrary material element.
Analytical cavity contraction solutions aim to provide distributions of stresses and displacements within the elasto-plastic zones around spherical and cylindrical cavities.Based on the geometrical analogies, cylindrical cavity contraction representing an incremental procedure of confinement loss is typically adopted as a fundamental model for ground responses at the tunnel crosssection, whereas the spherical scenario is capable of correlating to those at the face cross-section (Mair, 2008; Mo and Yu, 2017).
3. Rigorous large-strain solution for elastic medium
The elastic medium is assumed to obey Hooke’s law with linear relationships between stresses and strains:
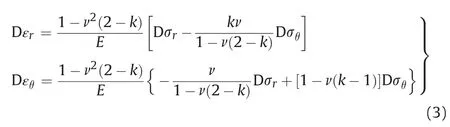
whereEandare the Young’s modulus and Poisson’s ratio,respectively; and D denotes the Lagrangian derivative for a given material element.
For convenience of derivation, the mean (p) and deviatoric (q)stresses can be expressed as follows (Mo and Yu, 2017):
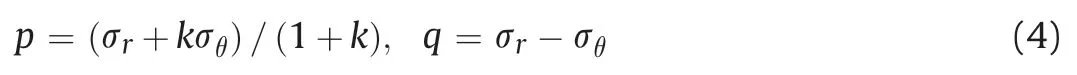
Similarly, the volumetric (εp) and shear (εq) strains are defined as

Substitution of Eqs. (4) and (5) into the elastic stressestrain relationships leads to the following expressions:
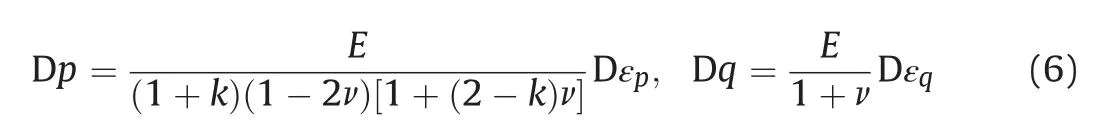
In order to transform the Eulerian description into the Lagrangian description, the approach of auxiliary variable c is adopted following Mo and Yu (2018), i.e.

Based on the assumptions of logarithmic strain (Eq. (2)), the volumetric and shear strains are rewritten as
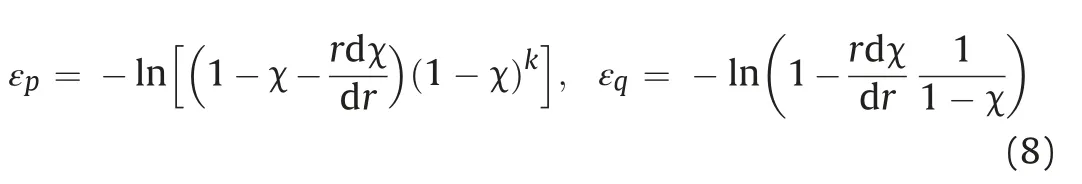
Thus, the equilibrium equation (Eq. (1)) can be expressed as a nonlinear first-order differential equation aboutqc, as follows:
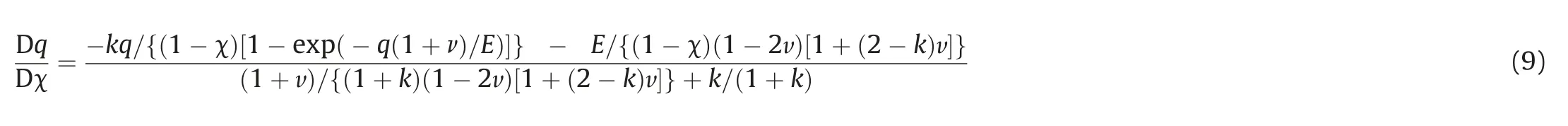
Together with the boundary conditions (qand c at infinite radius:q00,c00;c at cavity boundary:caaa0=a),the distribution ofqin terms of c can be obtained by solving the ordinary differential equation (Eq. (9)). The full distributions of stresses and strains are then calculated by the following explicit expressions:
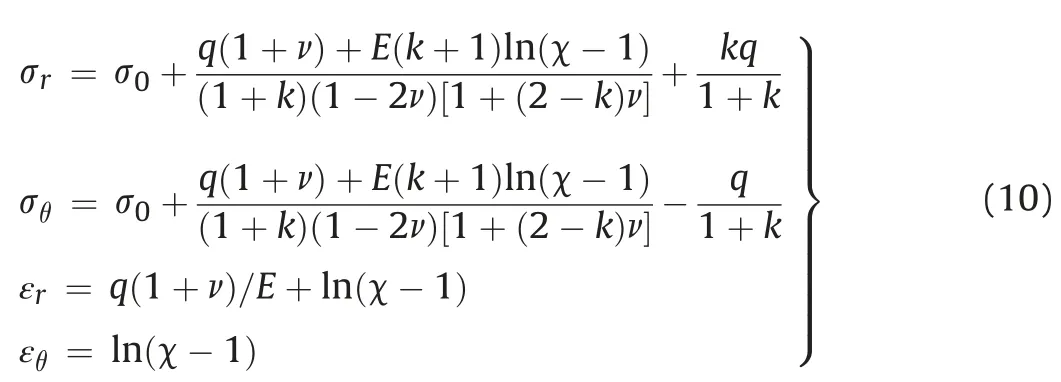
To determine the distributions in terms ofrrather than c, a numerical integration is required for the conversion between physical and auxiliary variables as follows:
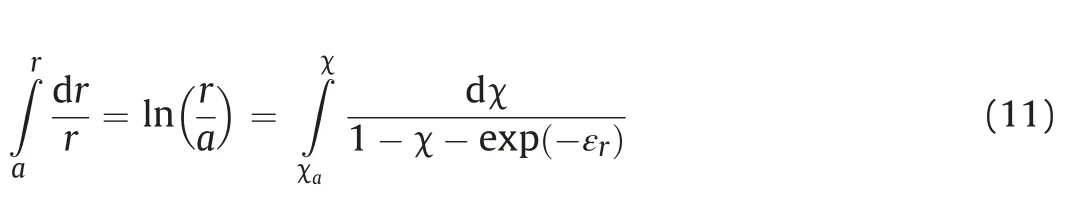
Combining Eq. (10) and integrations of Eq. (11) therefore gives the rigorous large-strain solution to cavity expansion or contraction in linearly elastic medium.
The proposed solution is referred to as rigorous solution, as it removes the assumption of small strains and is strictly derived for an arbitrary cavity contraction,leading to the conventional solution by Timoshenko and Goodier (1970)which is semi-analytical:
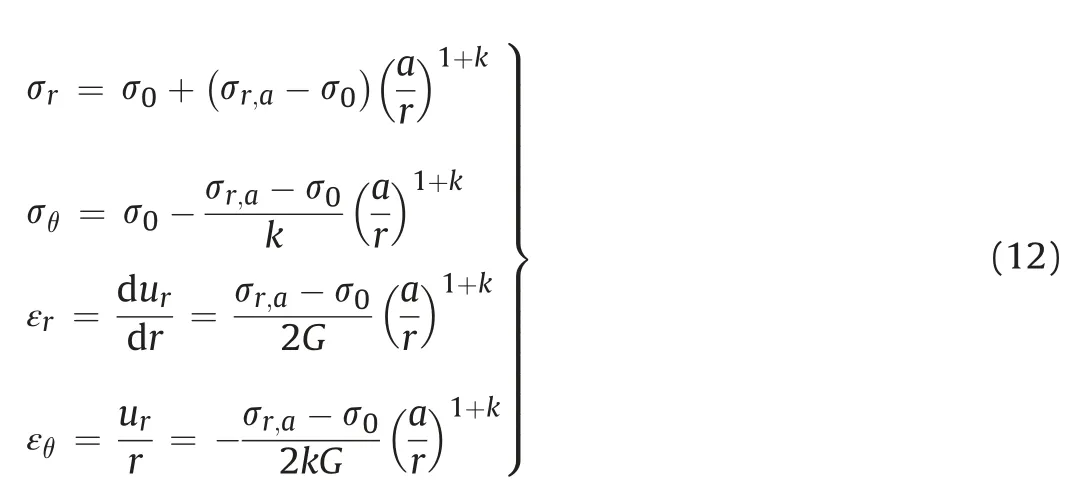
whereGis the shear modulus, defined asE=?21 t.
For a pressure-controlled cavity contraction problem with the following reference parameters: j0j100 kPa,E10 MPa and0:3 (representing a typical stiff clay or medium dense sand at about 5 m depth), Fig. 2 provides the validation of elastic solution against numerical results. Numerical simulation in this study was conducted using commercial finite element software ABAQUS 6.13(Dassault Systemes,2013).In consideration of geometric nonlinearity and large-deformation analysis,an axisymmetric model with 25,000 elements was established to simulate cylindrical cavity contraction.The statistical measure to the comparisons is given by the coefficient of determination,R2,and data from Fig.2 lead to the overall value ofR2>0:9999,indicating the accuracy of rigorous solution.
Although small-strain assumption was widely adopted in elastic zones by neglecting the higher order terms in logarithmic strains (e.g. Vrakas and Anagnostou, 2014; Vrakas, 2017), the derived formulations can only be treated as approximate rather than exact or rigorous solutions. Compared with the quadratures of Durban (1988), this solution simplifies the calculation to integrations of Eqs. (9) and (11), and the resulting expressions of stresses and strains are derived in the explicit forms, leading to the closed-form solution. The error analysis for comparing the approximate (xapprox:) and rigorous (xrigorous) solutions is conducted through the following expression in terms of any resulting indexx:
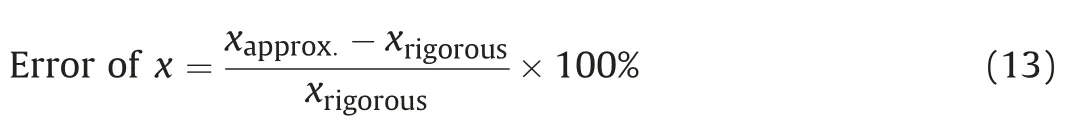
Taking the soil parameters in Fig. 2 as a reference, the error of cavity radius appears to increase exponentially with contraction,while overestimation is observed for cylindrical cavity and the spherical scenario behaves oppositely, as shown in Fig. 3a and b.The error of tangential stress during contraction is higher with several orders of magnitude than that of cavity radius,especially for cylindrical cavities (Fig. 3c).
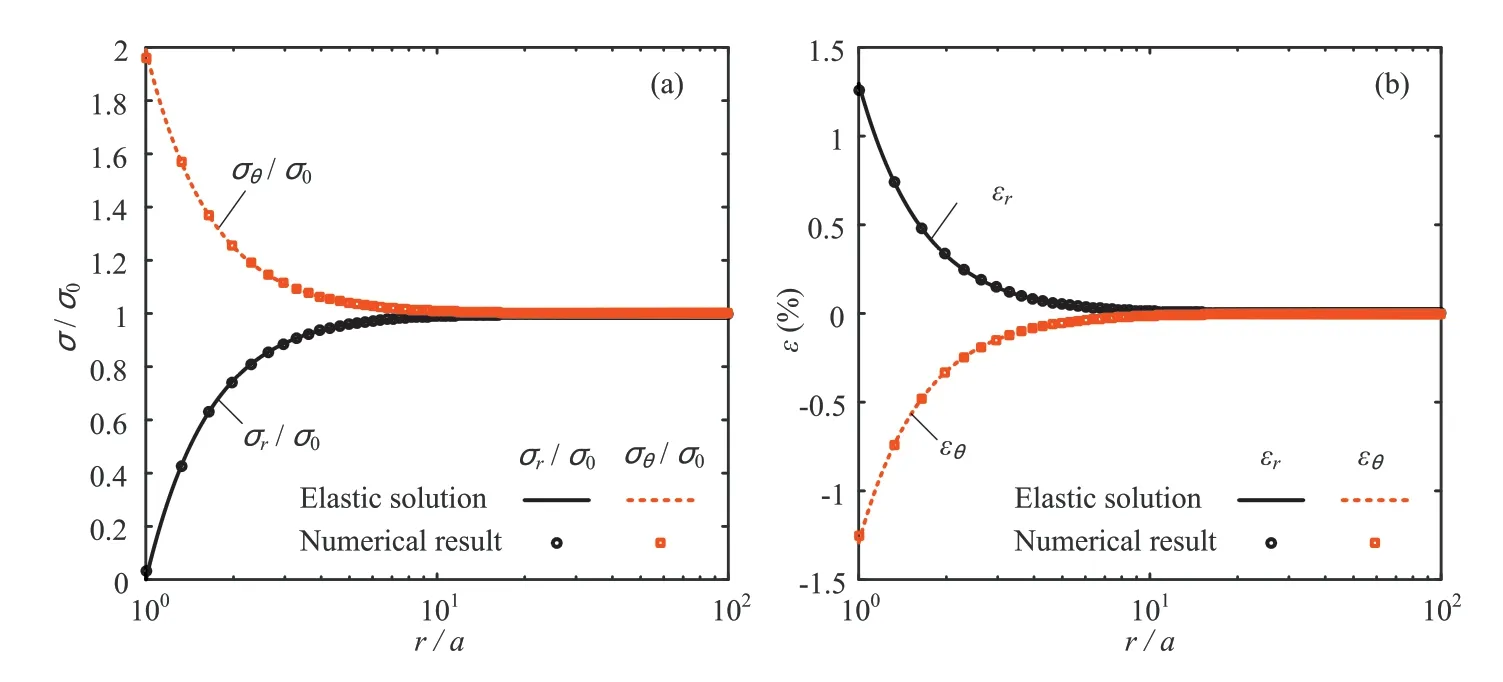
Fig. 2. Validation of elastic solution against numerical results for cylindrical cavity contraction: (a) Distributions of normalised stresses; and (b) Distributions of strains.
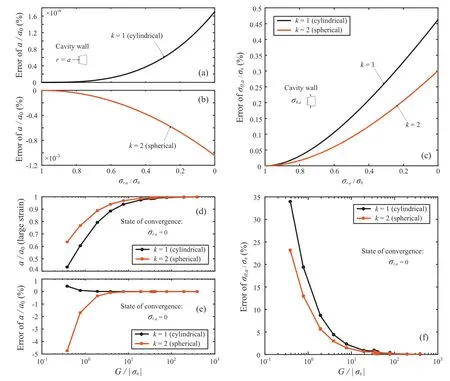
Fig. 3. Results of rigorous elastic solution compared with small-strain solution: (a) Error of cylindrical cavity displacement during contraction; (b) Error of spherical cavity displacement during contraction;(c)Error of tangential stress for cavity wall during contraction;(d)Variation of cavity displacement at state of convergence with stiffness ratio;(e)Error of cavity displacement at state of convergence with stiffness ratio; and (f) Error of tangential stress for cavity wall at state of convergence with stiffness ratio.
The parametric study of stiffness ratioG=j0j is examined and presented in Fig.3def,for contraction at the state of convergence(r;a0). The error of small-strain solution tends to be considerable when the stiffness ratio is less than 10. Considering the large deformation of tunnel excavation, the stiffness degradation is significant in terms of large strain level(Mair,1993).Shear strain of the elastic test rises up by 2.5% at the unsupported cylindrical cavity wall, where the stiffness is orders of magnitude smaller compared to the small-strain stiffness (Likitlersuang et al., 2013).Even in the elastoplastic analysis,the elastic stage typically yields to 1% of shear strain during excavation, while cyclic loading can lead to some level of stiffness degradation. Moreover, stress condition in deep tunnels contributes further to the decrease of stiffness ratio and thus the increase of approximation error. The deep urban subway tunnel has reached close to 100 m depth(Liu et al., 2017), whereas the deep tunnelling related to mining often exceeds 1000 m depth with in situ stress level over 30 MPa,such as the Jinchuan mine in Gansu, China (Yu et al., 2015). Therefore,the rigorous solution is necessary for analysing problems with large deformation, especially for deep underground construction with special stratum conditions.
Note that the provided solution is based on the assumption of linear elasticity, and nonlinearity and irreversibility are the two main features of geomaterials. When the concept of incremental nonlinearity is introduced,solutions for hyperelastic(derived from the elastic potential within the principles of thermodynamics)and hypoelastic models(i.e.purely phenomenologically-defined elastic models) can be extended in terms of the incremental form to provide more sophisticated elastic behaviour of geomaterials. The proposed large-strain solution can then serve as an important benchmark for validation of further developments in consideration of nonlinear elasticity and cyclic loading.Considering the plasticity of geomaterials,the elastic stage usually performs during the early loading process with limited deformation. Irrecoverable deformation plays a key role in plastic behaviour of geomaterials,and thus the large-strain assumption is indispensable for rigorous analysis.Despite of the relatively small error of small-strain solution in the elastic stage, the proposed rigorous large-strain solution can provide the continuity and consistency in the elasto-plastic regions without overcomplicating the derivations. The combination with typical plastic models will be described in the following sections.
4. Rigorous contraction solution for MohreCoulomb medium
Considering the shear strength of dilatant elasto-plastic media,the MohreCoulomb yield criterion with a non-associated flow rule is typically used to describe geomaterial behaviour. Cavity contraction in MohreCoulomb medium results in an inner plastic region surrounded by an outer infinite elastic region,and the radius of elasto-plastic boundary is denoted by ‘c’.Therefore,the rigorous large-strain solution presented in this section integrates the aforementioned large-strain elastic solution and the solution of Yu and Houlsby(1995)which neglected the effect of true strain in the elastic range.
For unloading of cavities,the yield condition of MohreCoulomb medium is expressed as

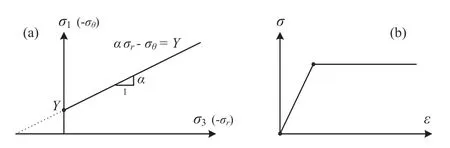
Fig. 4. (a) MohreCoulomb yield criterion and (b) Elasto-plastic stressestrain relation.
whereY2Ccos=1sinand a1 t sin=1sin,in whichandCare the friction angle and cohesion of geomaterials,respectively (see Fig. 4). Note that for cylindrical scenarios, the effect of axial stress is not included in this study,andzis assumed as the intermediate stress which was discussed to satisfy most realistic soil parameters by Yu and Houlsby(1995).Combining Eq.(14)and the distributions of stresses in the elastic region can give the magnitudes of radial stressr;c, tangential stresses;c, and the contraction ratioc0=c(1cc)at the elasto-plastic boundary(i.e.rc), which serve as the boundary conditions for the plasticregion solution.
The stresses in the plastic region are expressed in the following form satisfying the yield condition and the equilibrium equation:
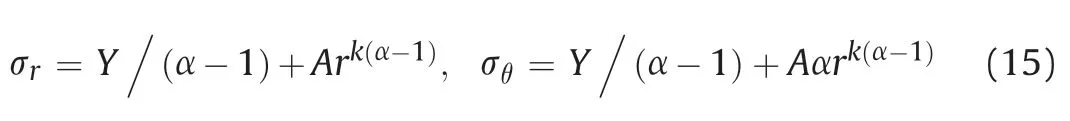
whereAis an integration constant,and boundary condition atrcleads toForcontraction of cylindrical and spherical cavities,the non-associated MohreCoulomb folw rule is

Substituting the large-strain assumptions (Eq. (2)), elastic stressestrain relations (Eq. (3)) and stresses in the plastic region(Eq. (15)) into the flow rule (Eq. (16)) leads to

where
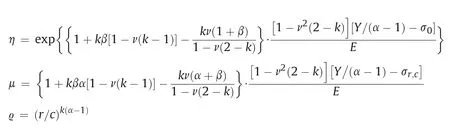
With the aid of the series expansion (Yu and Houlsby, 1995),integration of Eq. (17) over the interval betweenrandc(9c1)results in

where
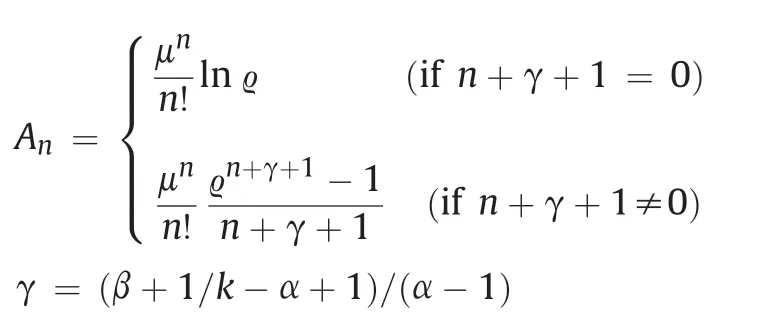
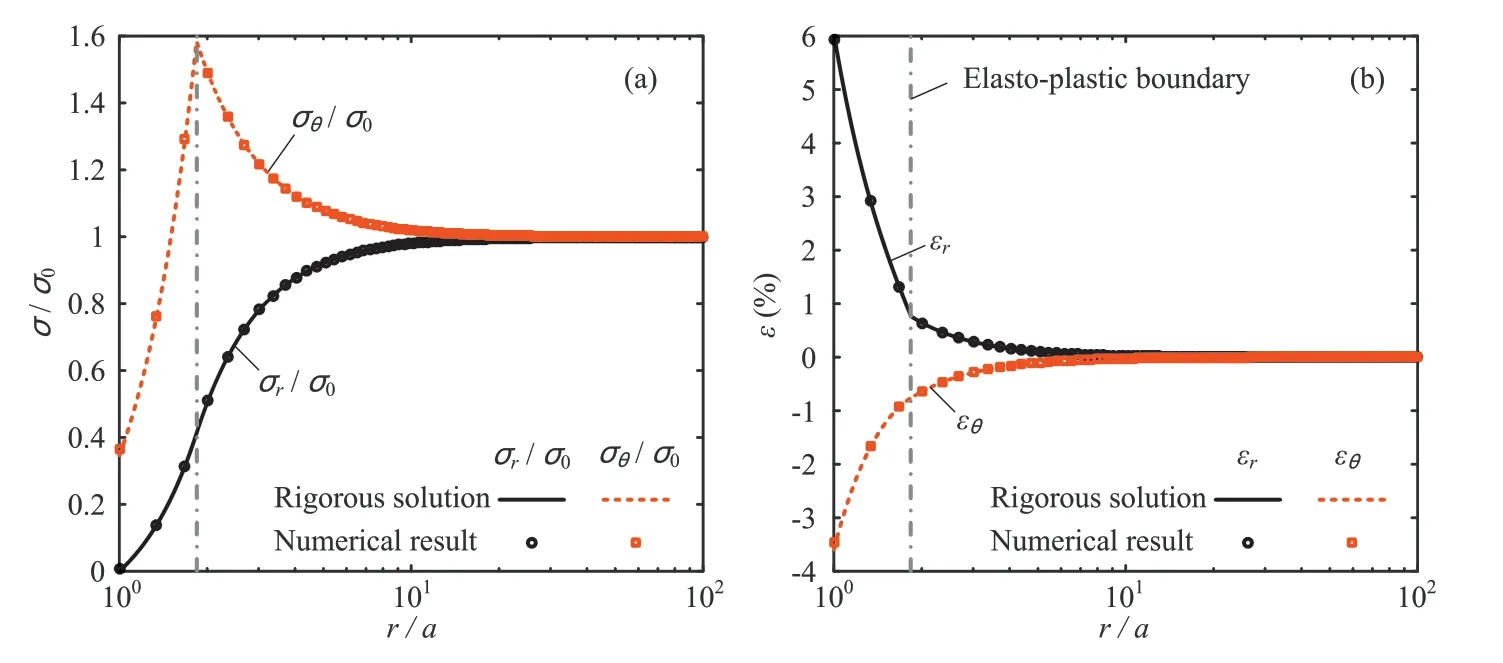
Fig. 5. Validation of MohreCoulomb solution against numerical results for cylindrical cavity contraction: (a) Distributions of normalised stresses; and (b) Distributions of strains.
For a given contracted cavity with radius ofa,full integration of plastic region based on Eq.(18)gives the amount ofc,c0,A,r;aandtogether with the relation ofThe displacement field in the plastic region is then calculated by given an arbitraryrin Eq. (18). The rigorous large-strain cavity contraction solution in MohreCoulomb medium is therefore obtained by combining both plastic and elastic regions.
Numerical validation of MohreCoulomb solution against numerical results is shown in Fig.5.Both elastic properties and stress condition are the same as last section; MohreCoulomb parameters are chosen as:cohesionC10 kPa,friction angle30,and dilation angle10.After complete unloading,the plastic region yields to 1.84 times the cavity radius, and the overall coefficient of determination givesR2>0:9998, validating the proposed rigorous solution. Note that a hyperbolic function in the meridional stress plane and a smooth elliptic function in the deviatoric stress plane are adopted as the flow potential of the MohreCoulomb model in Abaqus, which is slightly different to that used with Eq.(16)in this study.Comparing with the results of Vrakas and Anagnostou (2014), analysis of the Sedrun section of the Gotthard Base tunnel in Switzerland is revisited using the proposed solution. Fig. 6 shows the GRC and distributions of normalised displacement and stresses after excavation, and the comparisons indicate the accuracy of the analytical solution withR2>0:9997. Note that the numerical data incorporate the analytical results of Vrakas and Anagnostou (2014), in which the second order terms in the logarithmic strains in the elastic region was assumed to be negligible.Although the differences from Fig.5 are marginal in this case, errors would be introduced and cumulated when further analyses were applied. Despite of the differences on plastic flow, the rigorous analytical solution is validated against the numerical simulations.
Semi-analytical solutions of cavity contraction for MohreCoulomb material were also provided by Yu and Rowe(1999),which included a small-strain solution and an approximate large-strain solution,whose elastic deformation in the plastic region was neglected:

The error analysis is conducted with the following reference parameters:j0j100 kPa,E10 MPa,0:3,C10 kPa,30,and10.The variations of cavity radius at the state of convergence with cohesion and their errors are shown in Fig. 7a and b,respectively.The approximate large-strain solution seems to overestimate the cavity convergence, whereas the small-strain solution generally provides the underestimation. The error rises with the decrease of cohesion,and the cylindrical scenario appears to introduce more significant error.The effects of both friction and dilation angles are presented in Fig. 7c and d, respectively, indicating that the errors decrease withand, but the influence is weaker than that of cohesion.
5. Rigorous contraction solution for brittle HoekeBrown medium
Compared with the linear MohreCoulomb failure criterion(Eq.(14)),nonlinear yield criteria for geomaterials were used to analyse cavity unloading problems. The HoekeBrown failure criterion was proposed in 1980s originally for the design of underground excavation in isotropic intact rock(Hoek and Brown,1980), which was later updated to correlate the model parameters with the geological strength index(GSI)and damage factorD(Hoek et al.,2002;Hoek and Brown, 2019). HoekeBrown provides a nonlinear, parabolic relation between the major and minor principal stresses at failure,assuming independence of the intermediate principal stress.While the small-strain analytical solution of cylindrical cavity contraction in brittle HoekeBrown medium was developed by Brown et al.(1983) and Yu (2000), the current section presents a novel rigorous large-strain solution for both cylindrical and spherical scenarios.
For unloading of spherical and cylindrical cavities in this paper with tension positive notation, the initial yield condition is described as follows:

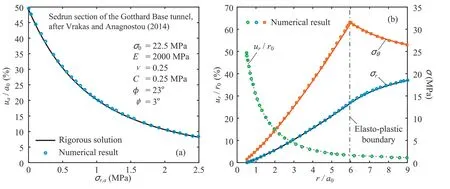
Fig.6. Comparisons of MohreCoulomb solution and numerical data for the Gotthard Base tunnel:(a)Ground reaction curve;and(b)Distributions of normalised displacement and stresses.
In order to describe the brittle-plastic behaviour of rock, the strength parameters are assumed to drop suddenly to their residual values after yielding. Thus, the failure criterion has the following expression:

wheresandmare the residual HoekeBrown constants. Fig. 8 shows the schematic of yield criterion and stressestrain relation for the brittle HoekeBrown medium.
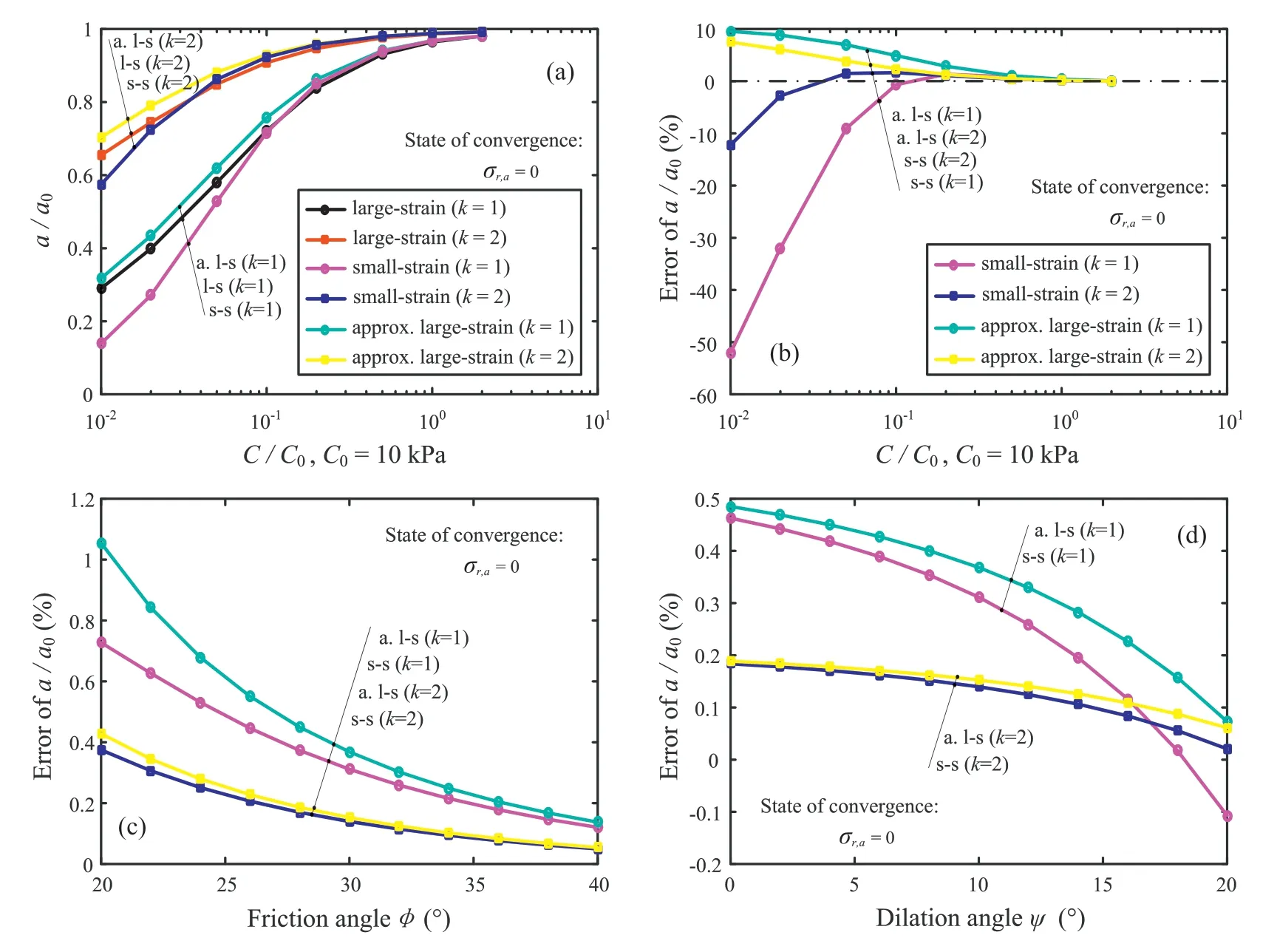
Fig.7. Results of rigorous MohreCoulomb solution at state of convergence compared with small-strain and approximate large-strain solutions:(a)Variation of cavity displacement with cohesion; (b) Error of cavity displacement with cohesion; (c) Error of cavity displacement with friction angle; and (d) Error of cavity displacement with dilation angle.

Fig. 8. (a) Yield criterion and (b) stressestrain relation for brittle HoekeBrown medium.
Similarly to the MohreCoulomb solution, for determination of the elasto-plastic boundary(rc),Eq.(20)is adopted to calculatetogether with the distributions in the elastic region. Combining equilibrium equation (Eq. (1)) and residual stress condition in the plastic region (Eq.(21)) leads to
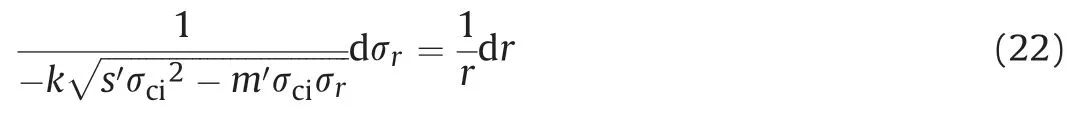
Applying the continuity of the radial stress at the elasto-plastic boundary,the spatial integration over the interval betweenrandcgives
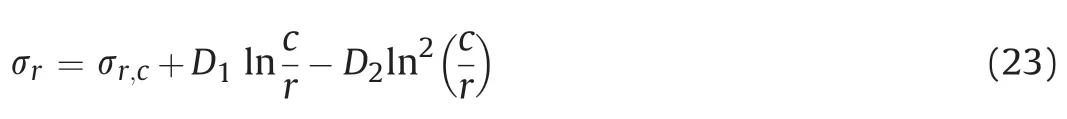
where
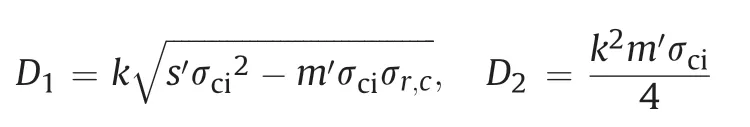
Substituting the differentiation form of Eq. (23) into the equilibrium equation, we have
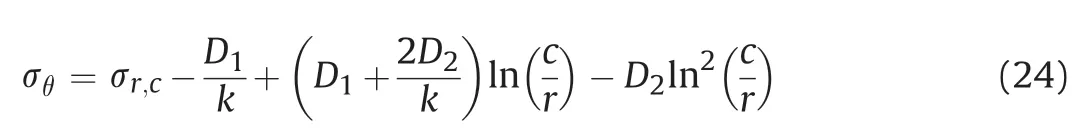
Together with the inequality of lnbased on the unloading condition, the boundary condition of Eq. (23) forrayields the relation betweenc=aand cavity pressurer;a:
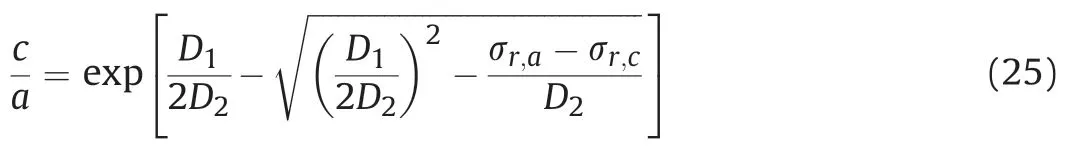
The non-associated flow rule(Eq.(16))is again employed for the large-strain analysis,and substitution of Eqs.(3),(23)and(24)leads to the following historical-integrated expression:
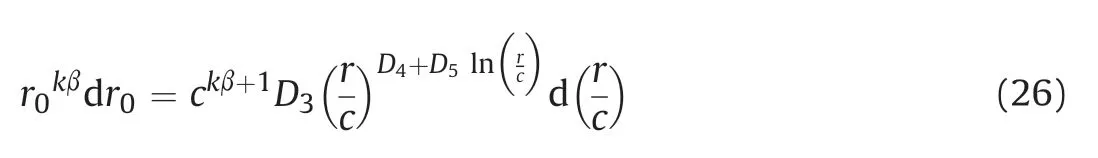
where
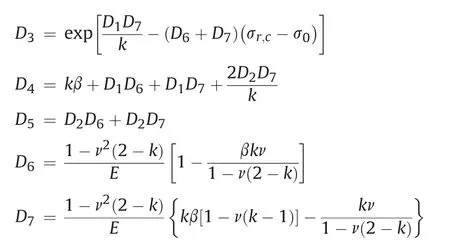
The spatial integration of Eq.(26)within the range ofraandrcis expressed as
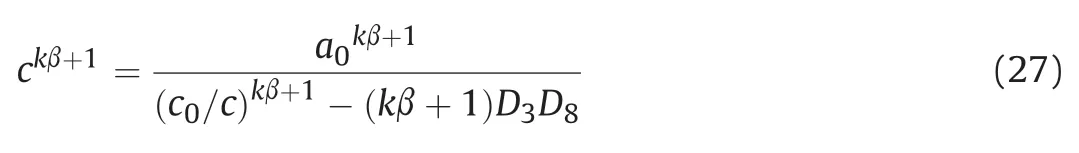
where
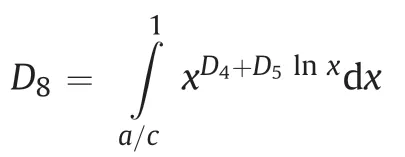
whereD8is a constant for a known value ofa=c. The calculation procedure is therefore suggested to be cavity pressure-controlled with a givenr;a, and Eq. (25) provides the magnitude ofc=a.Note that the cavity pressure needs to satisfy the following inequalityaccording to the yielding creteria. The value ofcis then solved by Eq. (27), following by the calculation ofc0anda. In terms of the distributions ofrandr0,integration of Eq. (26) betweenleads to
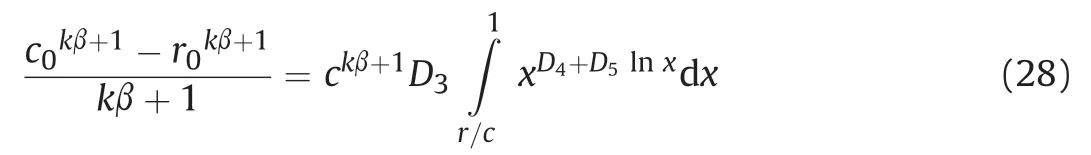
The following expression rewritten from Eq. (26) is used for calculation of radial strain:

It is noted that the rigorous large-strain solutions presented in this paper provide a general approach for cavity contraction problems, which is also applicable to other sophisticated constitutive models for geomaterials.
An example of cylindrical cavity in HoekeBrown criterion is provided with the following parameters:ci50 MPa,mi10,GSI45,D*0(D*0 for undisturbed in situ rock andD*1 for highly disturbed rock;a*0:5 is assumed according to the original HoekeBrown criterion). According to Hoek et al. (2002),the HoekeBrown constants are given withm1:4026 ands0:0022; assuming that the residual parameters are half of the magnitudes, i.e.m0:7013 ands0:0011. For best fitting of the HoekeBrown criterion with the MohreCoulomb parameters,the derived cohesion and friction angle are as follows:C12:14 kPa and37:2.
Fig. 9a shows the comparison of HoekeBrown and equivalent MohreCoulomb criteria, as well as the residual HoekeBrown failure criterion. The cavity contraction-pressure curves, representing the GRC or convergence-confinement curve, are presented in Fig. 9b, together with the rigorous elastic solution. Owing to the similarity of failure criterion, both HoekeBrown and Mohre Coulomb materials yield to their plastic state when the cavity pressure is reduced to approximately 0:290.Although the ultimate cavity convergences are comparable, it is obvious to notice the difference on the revolution of confinement-convergence. When considering the residual parameters after yielding, the cavity displacement is built up with contraction,as well as the sudden loss of tangential stress at the elasto-plastic boundary (Fig. 9c). Both radial and tangential strains at the cavity wall are provided in Fig. 9d, indicating the effects of plasticity and residual strength.
Fig. 9. Cylindrical results of rigorous HoekeBrown (HB) solution compared with MohreCoulomb (MC) solutions: (a) Comparisons of yield criteria; (b) Development of cavity displacement with contraction; (c) Development of tangential stress at cavity wall with contraction; and (d) Development of radial and tangential strains at cavity wall with contraction.
6. Results of deep tunnel convergence with support
While the analysis of cavity contraction can be directly adopted to obtain the GRC of a deep tunnel, supporting structure is typically installed to prevent the over large deformation after excavation.Similarly,the tunnel lining is reasonablyassumed as a cylindrical ring,experiencing an increase of pressure from zero at the outer boundary transmitting from the surrounding geomaterial. The tunnel lining structure is equivalently treated as elastic material withElandl.The outer and inner boundaries of the deformed lining are defined asalandbl,respectively.Thus,the thickness ofliningistlalbl.When the load is transmitted onto the lining, with the aid of small-strain assumption,the stiffness of lining is approximately defined as

When the thickness of lining is small enough compared to the tunnel diameter (tlal), the stiffness for cylindrical lining is simplified as

The derived lining stiffness determined the slope of the SCC, in combination with the GRC.The start of SCC represents the time or location of lining installation after excavation. As the lining installation is closed to the tunnel face, the tunnel convergence before supportur;dis comparable to the displacement based on spherical cavity contractionur;sph. When the installation is located at some distance behind the face, it is reasonable to setur;d>ur;sph. However, tunnel convergence might be smaller than the estimated displacement when the advance support technique is applied.Therefore, with the aid of combined spherical-cylindrical cavity contraction solutions, a lining installation factor x is introduced here to indicate the time of lining installation at the tunnel face,noting thatThe stress release coefficient is thus defined as

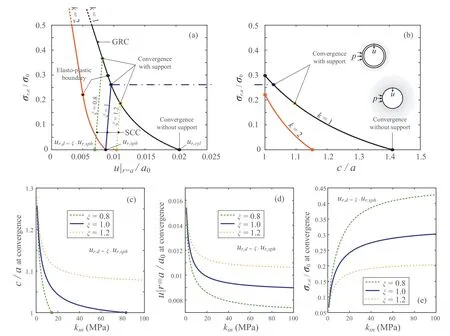
Fig. 10. Results of tunnel convergence with support: (a) Predicted GRC and SCC; (b) Plastic region at convergence with and without support; (c) Variation of plastic region at convergence with lining stiffness;(d)Variation of cavity displacement at convergence with lining stiffness;and(e)Variation of cavity pressure at convergence with lining stiffness.
whereur;maxis the radial displacement at convergence without support; andur;cylis the calculated radial displacement at convergence without support for cylindrical scenario.
With the same soil parameters as last section using Mohre Coulomb criterion, both spherical and cylindrical cavity contraction-pressure curves are calculated, and the SCCs with different values of lining installation factor are predicted by assumingksn30 MPa,as shown in Fig.10a.The intersections of SCCs with the GRC are estimated as the tunnel convergence with support.Note that the cavity pressure at convergence also indicates the grouting pressure behind the lining. In Fig. 10b, the developments of plastic region of both spherical and cylindrical cavities with contraction are shown. The convergence with support also indicates the magnitude of plastic region, compared with the situation without support. The parametric study, as presented in Fig. 10cee, ascertains the effects of lining installation factor and lining stiffness on the plastic region,cavity displacement and cavity pressure at state of convergence with support,which contributes to the design of deep tunnels.
Squeezing tunnel problems are critical to tunnel construction,as time-dependent large convergence occurs during excavation. In this study, the rate effect is considered by introducing the lining installation factor x, which represents the cavity deformation during the stage between excavation and support. However, determination of x requires empirical evaluation,and further development on cavity contraction solutions with rate-dependent constitutive models would give detailed analytical illustration.It should also be noted that anchors and/or cables are typically used to support deep tunnels in cooperation with bolt-concrete supports. The surrounding rock loose circle supporting theory is suggested to estimate the equivalent inner layer with supporting structures, after Dong and Song (1994). This method can provide accurate and rapid determination of equivalent thickness of loose circle,and this layer is thus taken as the supporting layer for the design of deep tunnels.
The proposed rigorous large-strain cavity contraction solutions provide benchmarks for analyses of deep tunnel convergence in geomaterials. The elastic solution applies for preliminary stability analysis,and it is also suitable for tunnels with strict requirements on deformation. The elastic analysis could be extended to underground structures including lining layers. The MohreCoulomb solution employs the classical MohreCoulomb yield criterion and non-associated flow rule, and has wide applications for tunnels in typical soils under essentially monotonic loading. For tunnels in rocks, the HoekeBrown solution is suggested, which adopts a nonlinear yield criterion. The brittle effect is more preferable to breakable rocks or soils with obvious softening. However, the limitations need to be mentioned for applications. The solutions assumed the geomaterials as homogenous and isotropic, and tunnels in layered soil need further considerations on the layering profile.Shallow embedded tunnel also requires investigation on the surface effects. The current analyses focused on the rateindependent behaviour of geomaterials, whereas the dynamic and rheological phenomenon may be important for tunnels in soft geomaterials. In terms of tunnel geometry, solutions should be modified accordingly for rectangular, elliptic or other irregularly shaped tunnels.
7. Conclusions
Rigorous large-strain solutions of unified spherical and cylindrical cavity contraction in linearly elastic, non-associated Mohre Coulomb, and brittle HoekeBrown media are proposed in this paper, which provide a general approach for solutions using other sophisticated geomaterial models and benchmarks for analytical developments and numerical analyses of underground excavation.
The approximation error showing the discrepancy between the previous and current solutions indicates the necessity of release of small-strain restrictions for estimating tunnel convergence profiles.Stiffness degradation and higher stress condition for deep tunnels result in reduction of stiffness ratio,which shows considerable errors for elastic scenarios.The GRC is therefore predicted by rigorous solutions, describing the volume loss and stress relaxation around the tunnel walls, as well as the SCC of the installed lining around the opening face.
The stiffness of circular lining is calculated from the geometry and equivalent modulus of the supporting structure, and a lining installation factor is introduced to indicate the time of lining installation based on the prediction of spherical cavity contraction for tunnel face.The parametric studies thus ascertain the effects of material properties,lining stiffness and lining installation factor on the stress/strain evolutions, generated plastic region and groundsupport interaction, during the incremental procedure of confinement loss.
Declaration of Competing Interest
The authors wish to confirm that there are no known conflicts of interests associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Acknowledgments
The authors would like to acknowledge financial supports from the Foundation of Key Laboratory of Transportation Tunnel Engineering (Southwest Jiaotong University), Ministry of Education,China(Grant No.TTE2017-04),National Natural Science Foundation of China (Grant No. 51908546), and Natural Science Foundation of Jiangsu Province (Grant No.BK20170279).
List of symbols


 Journal of Rock Mechanics and Geotechnical Engineering2020年3期
Journal of Rock Mechanics and Geotechnical Engineering2020年3期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Crack initiation of granite under uniaxial compression tests: A comparison study
- Reliability analysis of slopes considering spatial variability of soil properties based on efficiently identified representative slip surfaces
- Critical state model for structured soil
- Coupled hydro-mechanical analysis of expansive soils: Parametric identification and calibration
- A modified soil water content measurement technique using actively heated fiber optic sensor
- Damage characteristics and catastrophic failure mechanism of coal rock induced by gas adsorption under compression
