空間自回歸模型誤差分布估計的漸近性質(zhì)*

曾慶樊

(廣西師范大學 數(shù)學與統(tǒng)計學院,廣西 桂林 541004)

0 引言

隨著經(jīng)濟的快速發(fā)展以及對數(shù)據(jù)的收集更加完整,在實際數(shù)據(jù)中,數(shù)據(jù)往往是具有空間關聯(lián)性的,由此空間計量經(jīng)濟學受到許多國內(nèi)外學者的關注.在理論研究與應用領域都得到快速發(fā)展.1973年Cliff和Ord[1]出版的Spatial autocorrelation首次考慮到了空間效應,提出了空間自回歸模型;Anselin[2]于1998 年出版的Spatial Econ metrics:Methods an d Models對空間計量經(jīng)濟學理論做出了系統(tǒng)的整理.2004年LEE[3]證明了空間自回歸模型擬極大似然估計的漸近性質(zhì);2010年Lee和Yu[4]建立了具有固定效應和空間自回歸擾動的空間自回歸面板數(shù)據(jù)模型的擬最大似然估計的漸近性質(zhì).

本文考慮如下空間自回歸模型:

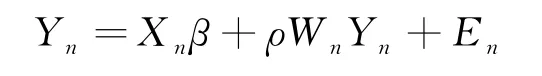
其中n為空間單位總量,X n=(x1,x2,…,x n)'是n×k固定設計自變量的觀測值,Y n=(y1,y2,…,y n)'是n×1隨機變量的觀測值,W n=(w1,w2,…,w n)'是一個預先給定的n×n維空間權重矩陣,ρ∈R為自回歸參數(shù),β∈R k是參數(shù)向量,E n=(e1,e2,…,e n)'為獨立同分布的隨機誤差項,其中e i具有未知的分布和密度函數(shù)f(x),且滿足

ρ的對數(shù)似然估計為

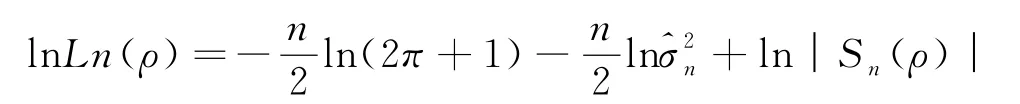
ρ的擬極大似然估計^ρn為上式極大化的值.

以往在對參數(shù)進行估計時,我們通常假定e i是服從正態(tài)分布的,但是在許多實際問題中正態(tài)性假定并不合理,此時參數(shù)估計的結(jié)果也并不理想.因此估計e i的未知分布和密度函數(shù)具有十分重要的意義.關于誤差分布估計的研究并不多,柴根象[5]研究了線性模型誤差分布估計的漸近性質(zhì).許冰[6]利用進一步一般化了柴根象的結(jié)果,定義了更廣泛的f(x)的估計形式.楊瑛[7]研究了非參數(shù)回歸模型誤差分布估計的大樣本性質(zhì).楊亞寧、趙選民[8]研究了半?yún)?shù)回歸模型誤差分布估計的大樣本性質(zhì),在一定條件下證明了估計依概率收斂.本文將誤差分布估計推廣到空間數(shù)據(jù)模型上,研究了空間自回歸模型誤差分布估計的漸近性質(zhì),在一定條件下得到了f(x)的估計f^n(x)依分布收斂.

1 主要結(jié)果