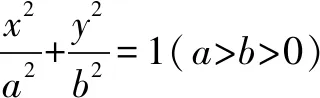一道質(zhì)檢試題的解析和探究

蘇藝偉

(福建省龍海第一中學新校區(qū) 363100)

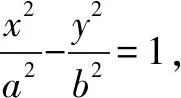
圖1

試題分析本題既樸實又創(chuàng)新.樸實之處在于以常見的直線與雙曲線相交為載體,結(jié)合對稱性,考查雙曲線中基本量的運算,屬于學生熟悉的題型;創(chuàng)新之處在于給出的條件為兩個角度,且為倍數(shù)關(guān)系,讓人有一種陌生但是又耳目一新的感覺.看到此試題,覺得有思路可以做,但是細心做下去又覺得有一定的難度,具有一定的挑戰(zhàn)性.

解法分析

1.考慮特殊情況

如圖1,題目中的點P在x軸上運動,但是具體位置并不知道,這就給題目增加了難度,一時之間感覺難以入手.退一步想,既然點P是動點,那不妨先假設(shè)點P就是右焦點.以退為進,看看能否求解.

解析假設(shè)點P為雙曲線的右焦點,則P(c,0).設(shè)M(x1,y1),N(x2,y2),Q(-x1,-y1).

(b2-3a2)2x2+6a2cx-3a2c2-a2b2=0,

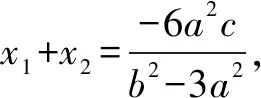
通過上述解題過程,發(fā)現(xiàn)對于點P為雙曲線右焦點的情況,是可以求出離心率的.而且在(1)式中,c被約掉了,這就引導我們思考:本題的求解跟點P在x軸的具體位置是否無關(guān)?

2.考慮一般情況

假設(shè)點P(x0,0).設(shè)M(x1,y1),N(x2,y2),Q(-x1,-y1).

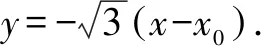
(b2-3a2)2x2+6a2x0x-3a2x02-a2b2=0,

在上述解題過程,發(fā)現(xiàn)對于(2)式,x0被約掉了,這就啟發(fā)我們其實本題的求解跟點P在x軸的具體位置無關(guān).因此,對于本題,采用了特殊化策略,先考慮特殊情況,得到結(jié)論,由此受到啟發(fā),再考慮一般情況,以退為進.如此一來,化抽象為具體,降低了思維難度,順利求解.

下面,筆者對此題進行了若干探究.

探究1 是不是當∠MPO=2∠MNQ時,該雙曲線都是等軸雙曲線?

分析取∠MPO=30°,∠MNQ=15°.假設(shè)點P(x0,0).設(shè)M(x1,y1),N(x2,y2),Q(-x1,-y1).

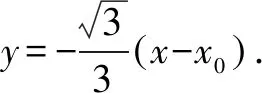
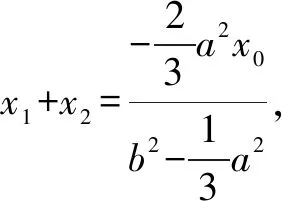
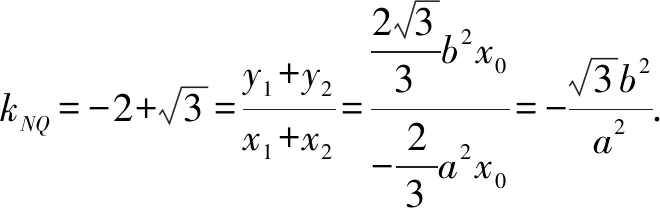
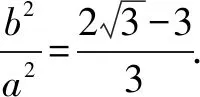
結(jié)論1 當∠MPO=2∠MNQ,該雙曲線不一定都是等軸雙曲線.

探究2 若該曲線為等軸雙曲線,則∠MPO=2∠MNQ一定成立嗎?

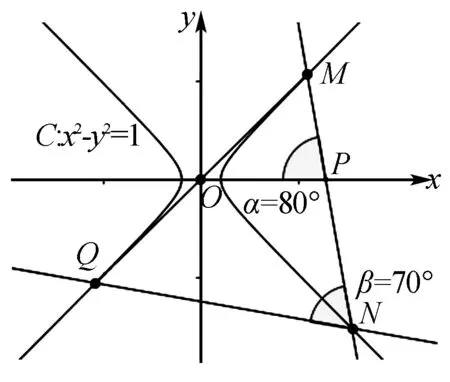
圖2

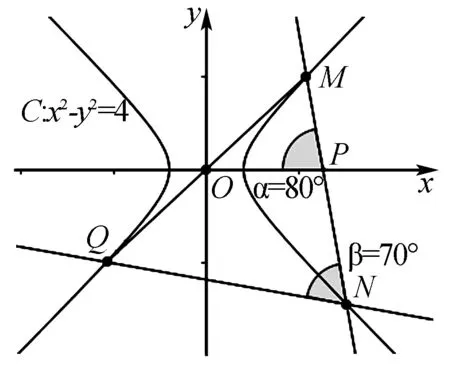
圖3

分析借助Geogebra軟件進行驗證.作出等軸雙曲線x2-y2=1,利用定值角度工具作出∠MPO=80°,然后利用角度工具測量出∠MNQ的度數(shù),為70°.再拉動點P,可以發(fā)現(xiàn)∠MNQ保持定值70°.對于等軸雙曲線x2-y2=4,情況也是一樣的.如圖2,圖3所示.

結(jié)論2 若該曲線為等軸雙曲線,則∠MPO=2∠MNQ不一定成立.

至此,我們可以清楚地意識到,題目中的條件“若∠MPO=60°,∠MNQ=30°”,通過計算和驗證可以得到該雙曲線為等軸雙曲線,但是并不意味著∠MPO=2∠MNQ與該雙曲線是等軸雙曲線有必然的關(guān)系.題目給出這樣的條件其實是降低了試題的難度,因為這兩個角都是特殊角,可以計算出正切值.

探究3 當∠MPO=2∠MNQ時,該雙曲線的離心率如何求解?

分析不妨設(shè)∠MNQ=α,則∠MPO=2α.假設(shè)點P(x0,0).設(shè)M(x1,y1),N(x2,y2),Q(-x1,-y1).

直線MN方程為y=-tan2α·(x-x0).代入雙曲線方程得

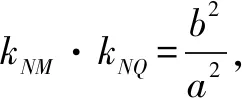
試題變式