Three-dimensional finite-time cooperative guidance for multiple missiles without radial velocity measurements
Teng LYU,Chuanjiang LI,Yanning GUO,Guangfu MA
Department of Control Science and Engineering,Harbin Institute of Technology,Harbin 150001,China
KEYWORDS 3-D cooperative guidance;Directed communication topologies;Finite time;Impact angle constraint;Radial velocity measurements
Abstract In order to simultaneously attack a target with impact angle constraint in threedimensional(3-D)space,a novel distributed cooperative guidance law for multiple missiles under directed communication topologies is proposed without radial velocity measurements.First,based on missiles-target 3-D relative motion equations,the multiple missiles cooperative guidance model with impact angle constraint is constructed.Then,in Line-of-Sight(LOS)direction,based on multiagent system cooperative control theory,one guidance law with directed topologies is designed with strict proof,which can guarantee finite time consensus of multiple missiles'impact times.Next,in elevation direction and azimuth direction of LOS,based on homogeneous system stability theory and integral sliding mode control theory,two guidance laws are proposed respectively with strict proof,which can guarantee LOS angles converge to desired values and LOS angular rates converge to zero in finite time.Finally,the effectiveness of the designed cooperative guidance law is demonstrated through simulation results.
1.Introduction
Nowadays,more and more modern targets are equipped with advanced anti-air defense missile systems and Close-in Weapon System(CIWS).In order to enhance the survivability of missiles,simultaneous attack strategies have been studied in these years.As one of the effective ways to realize simultaneous attack,cooperative guidance has attracted much attention,in which multiple missiles communicate among themselves to synchronize the arrival times.1-12In the process of cooperative guidance law design,there are six problems quite worth studying,i.e.,3-D cooperative guidance,2-4directed communication topology,5-9impact angle constraint,6moving target,2,10,11finite time consensus,9,10,12without radial velocity measurements.13
3-D cooperative guidance laws are more applicable for engineering practice than two-dimensional (2-D) guidance laws.Traditional cooperative guidance laws are designed in 2-D space.1,5-12In order to extend the cooperative guidance law to 3-D,2-4Zhao et al.2proposed the cooperative guidance law by combining a time-to-go coordination component with the traditional 3-D PN component in the pitch loop and yaw loop.Later,based on the receding horizon control technique,Zhao and Zhou3presents the cooperative guidance law against stationary target.Based on the guidance model in LOS direction,Song et al.4proposed the cooperative guidance law which can make missiles'impact times achieve consensus in finite time through adjusting missiles'thrust values.Although the cooperative guidance laws mentioned above is 3-D,their communication topologies have to be undirected and they have to employ the radial velocity measurements.
In practical engineering,multiple missiles'communication topologies could be directed due to the communication equipment failure or different missiles'communication ranges.Traditional cooperative guidance laws assume that communication topologies should be undirected.1-4,10-12In order to design cooperative guidance laws with directed topologies,5-9Zhang et al.5proposed the cooperative guidance law by combining the biased cooperative guidance term under directed topologies with the traditional proportional navigation guidance term.Later,Wang et al.6extended it to guidance law with impact angle constraint.Based on the traditional impact-timecontrol guidance law,Song et al.7proposed the cooperative guidance law under the assumption that the communication network of multiple missiles is strongly connected.Based on the second-order multi-agents cooperative control theory and traditional PN guidance law,Zhao et al.8proposed the cooperative guidance law which needs to have a directed spanning tree.Zhou and Yang9proposed the guidance law in both the LOS direction and normal direction of LOS,the communication topology of which is a leader-follower graph.Even though the studies above considered the problem of directed communication topology,they had to measure the radial velocities and did not consider target's mobility.
Cooperative guidance laws with impact angle constraint can make multiple missiles attack the target in desired directions,which will enhance missiles'survivability,damage ability and observability of target,and protect missiles from colliding with each other during the flight.Traditional cooperative guidance laws are designed without impact angle constraint.1-5,7-12In order to improve the corresponding performance of missiles,Wang et al.6combined the impact-angle-control guidance term with the cooperative guidance term to achieve impact angle constraint and consensus of impact times.Nevertheless,target's mobility were not considered.
With the development of technology,more and more targets have the ability to move.Traditional cooperative guidance laws assume that the target should be statistic.1,3-9,12In order to improve the impact precision of missiles,some guidance laws are designed against moving targets.2,10,11Zhang et al.10solved the problem through adopting the PN guidance law in the normal direction of LOS,which can make missiles impact moving target.Zhao et al.2,11proposed the cooperative guidance law by combining the time cooperative guidance term with the acceleration estimates of the target.Even though the literatures above considered the target's mobility,they did not consider the problem of directed communication topology.
Impact times'finite time consensus is beneficial for missiles to penetrate enemies'air defense systems.Traditional cooperative guidance laws can only make missiles'impact times reach consensus asymptotically.1-8,11In order to make missiles'impact times achieve consensus in finite time,9,10,12Zhou et al.9proposed the cooperative guidance laws in both the tangential and normal direction of velocity vector.The normal accelerations are under the PN structure and can adjust the curvatures of the missiles'trajectories,while the tangential accelerations can adjust the magnitudes of the missiles'speeds.Zhang et al.10proposed the cooperative guidance law based on the multiagent first-order finite time consensus theory.Hou et al.12added a time-varying gain ratio term into the PN guidance law which can realize finite time consensus.Although the guidance laws listed above could achieve impact times'finite time consensus,they did not consider impact angle constraint and had to measure radial velocities.
Guidance laws without radial velocity measurements can avoid adopting the corresponding sensors,which can lower seekers'costs and complexity and improve the system's reliability.Besides,for some missiles already designed which need radial velocity measurements,once their corresponding sensors fail to work,the guidance system will fail to work too.Thus,the guidance laws without radial velocity measurements can act as the alternate algorithm.Therefore,studies on designing the guidance laws have great significance in practical engineering.Although Lv et al.13could achieve impact times'finite time consensus without radial velocity measurements,they did not consider 3-D cooperative guidance.
To the best knowledge of the author,even though nearly each of the six problems listed above has been studied in the existing literatures,studies considering all the six problems together are rare.Motivated by the practical necessity of it and the limitations of aforementioned literatures,1-12we are proposing a novel cooperative guidance law which considers all of the six problems.Firstly,in the LOS loop,the distributed finite time guidance law under directed communication topologies without radial velocity measurements is proposed with strict proof.Then,in both the elevation and azimuth loops,two guidance laws are proposed respectively with strict proof for missiles to attack the moving target in desired directions.Neither of the two guidance laws needs to measure the radial velocity.The mobility of the target is regarded as the guidance system's external disturbance and suppressed by the super-twisting integral-sliding-mode control method. Finally, numerical simulations are given to demonstrate the effectiveness of the proposed cooperative guidance law.
The main contributions of this paper are summarized as follows:(A)compared with Refs.1-13,all the six problems stated above are considered together in this paper,i.e.,3-D cooperative guidance,directed communication topology,impact angle constraint,moving target,finite time consensus and guidance without radial velocity measurements,which is beneficial for practical implementation. (B) Compared with Refs.1,2,11,12,the communication topology of the proposed guidance law is distributed rather than centralized,which can lower the requirement for communication distance between two missiles.(C)Compared with Refs.6,14,the communication topology of the proposed guidance law is leaderless,which can avoid the risk of single point failure problem caused by leader-follower architecture.(D)Compared with Refs.2,11,the proposed guidance law does not need to measure target's velocity and acceleration,which can reduce the seekers'cost and complexity.(E)Compared with Refs.3,7,the proposed guidance law is time-continuous,which can protect missiles'actuators from chattering.
2.Preliminaries and problem formulation
2.1.Preliminaries
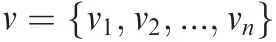

Note that in this paper, any given a vectorand a constant μ >0, define and
Lemma 118.If the directed graph G is strongly connected and detail-balanced, there exists a positive column vector θ=such that θiaij=θjajifor all i,j ∈ {1 ,2 ,...,n}.Denote Θ=diag(θ1,θ2,...,θn),then ΘL=(ΘL)T.
Lemma 219.If the directed graph G is strongly connected,the rank of G's Laplacian matrix L can be expressed as rank(L)=n-1.
Lemma 320.Consider n-dimensional system
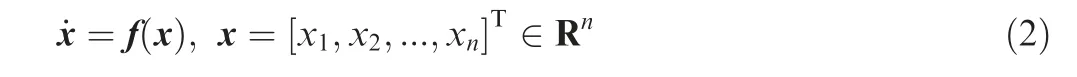
Suppose system Eq.(2)is homogeneous of degree σ with dilation (r1,r2,...,rn) and f(x) is continuous. If σ <0 and x=0 is the system's asymptotically stable equilibrium,it is the system's finite-time stable equilibrium.
Lemma 421.Assume that a continuous positive definite function V(t)satisfies the differential inequalitywhere τ >0 and 0 <η <1.Then,the system's states will converge to the equilibrium point in finite time
Lemma 522.For χ ∈(0,1)and ξ1,ξ2∈R,the feedback law
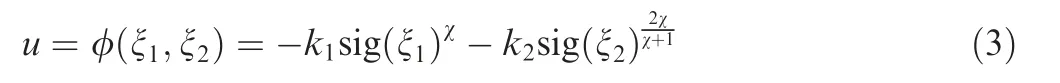
renders the origin finite-time stable for the double integrator system

where k1>0,k2>0.
Remark 1.In this paper,the related variable's subscript M represents missile,T represents target,i represents the index of missile,f represents final moment,go represents time-togo,r represents radial direction of LOS,ε represents elevation direction of LOS,β represents azimuth direction of LOS,nom represents nominal,max represents maximum and min represents minimum.
2.2.Problem formulation
In this section,the multiple missiles 3-D cooperative guidance model with impact angle constraint is constructed.The following assumptions are considered for the analysis and design of the guidance laws2:
Assumption 1.The missiles and target are considered as point masses moving in the 3-D space.
Assumption 2.The seeker and autopilot dynamics of the missiles are fast enough in comparison with the guidance loop.
Assumption 3.The target is stationary or moving with constant velocity.
Under the prescribed assumptions above, the guidance geometry on one-to-one engagement in three dimension is depicted in Fig.1,where Midenote the ith missile,respectively.Mixyz is a inertial reference.Mix1iy1iz1iis a LOS frame.riis the relative distance between target and Mi.qεiand qβiare elevation and azimuth LOS angles,respectively.
According to the principles of kinematics,the 3-D guidance geometry as shown in Fig.1 can be expressed by the following differential equations23,24:
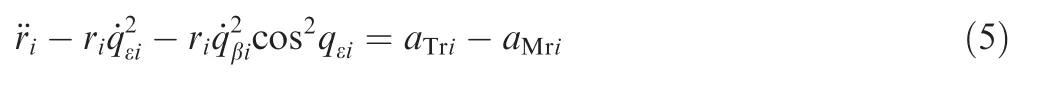

Fig.1 3-D missiles-target interception geometry.
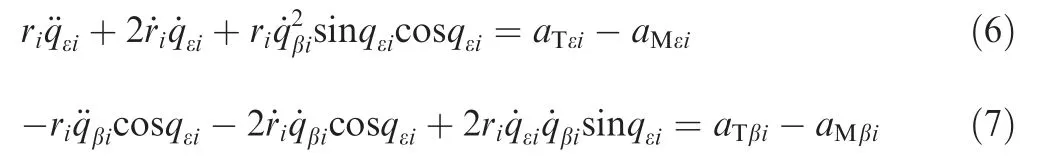

The impact angle is defined as the intersect angle between velocity vectors of the missile and the target at the impact time.Based on Ref.25,the guidance problem with the impact angle constraint is converted to the control problem of terminal LOS angle.The constraint on LOS angles in the elevation direction and azimuth direction can be expressed as follows:

where tfrepresents the impact time,qεdiand qβdidenote the desired terminal elevation and azimuth LOS angles,respectively.
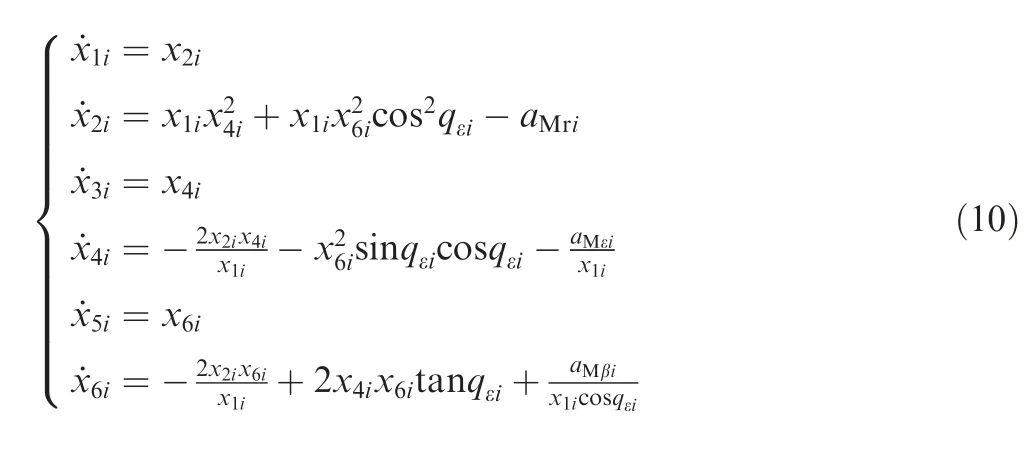
Remark 2.In practical engineering,ri,qεiand qβican be measured directly by the three-coordinate radar.andcan be obtained through filtering the information of qεiand qβi.can be measured directly by the PD(Pulse Doppler)radar.Thus,it can be seen that the variablesandcan be obtained without using the information of,and vice versa.
Remark 3.Some of the nonlinear coupled terms in the 3-D guidance system can be measured and offset by adding the opposite terms in the guidance law,and other nonlinear coupled terms can be regarded as external disturbance and compensated by integral sliding mode control method.Thus,the 3 guidance laws can be designed separately.
3.Cooperative guidance law design
In this section,a novel cooperative guidance law which is composed of three components in the LOS coordinate system is designed.Firstly,in Section 3.1,the cooperative guidance law's component in the direction of LOS aMriis designed with strict proof.Then,in Section 3.2,the cooperative guidance law's other two components aMεiand aMβiin the elevation and azimuth direction of LOS are designed respectively with strict proof.Finally,the advantages of the cooperative guidance law are listed.
3.1.Design of guidance law in the direction of LOS
In this subsection,based on multi-agent cooperative control theory13,18,26-33and state observer theory,34a novel guidance law in the direction of LOS is proposed to ensure that the relative distance x1iand its rate x2ican achieve consensus in finite time without measurements of x2i.Thus,the consensus of multiple missiles'impact times is achieved in finite time.
From Eq.(10),the guidance model in the direction of LOS can be expressed as follows:
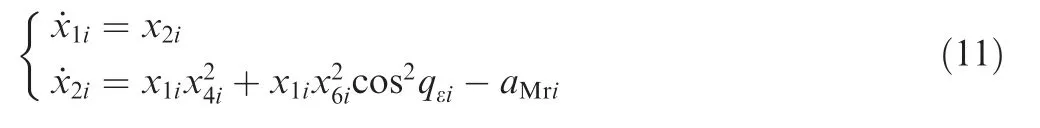
The impact time tfiof Mican be expressed as follows:

From Eq.(12)it can be known that tfi-tfj=tgoi-tgoj.Thus,if tgoican achieve consensus,tfiwill achieve consensus at the same time.In practical terminal guidance process,the variation of the missile-target radial velocityis relatively small.Thus,tgoican be estimated precisely enough by the following equation:

Therefore,the design objective is to develop the guidance law aMri,which can make x1iand x2iin Eq.(11)achieve consensus in finite time without measuring x2i.That is,

Thus,it can be known from Eqs.(13)and(14)that tgoican achieve consensus in finite time.
The novel guidance law is proposed as follows and its proof is presented afterwards.
Theorem 1.Considering system Eq.(11)with communication topology G that is directed,strongly connected and detailed balanced,the guidance law in the direction of LOS as is shown in Eqs.(15)-(18)can make x1iand x2iachieve finite time consensus without measuring x2i.
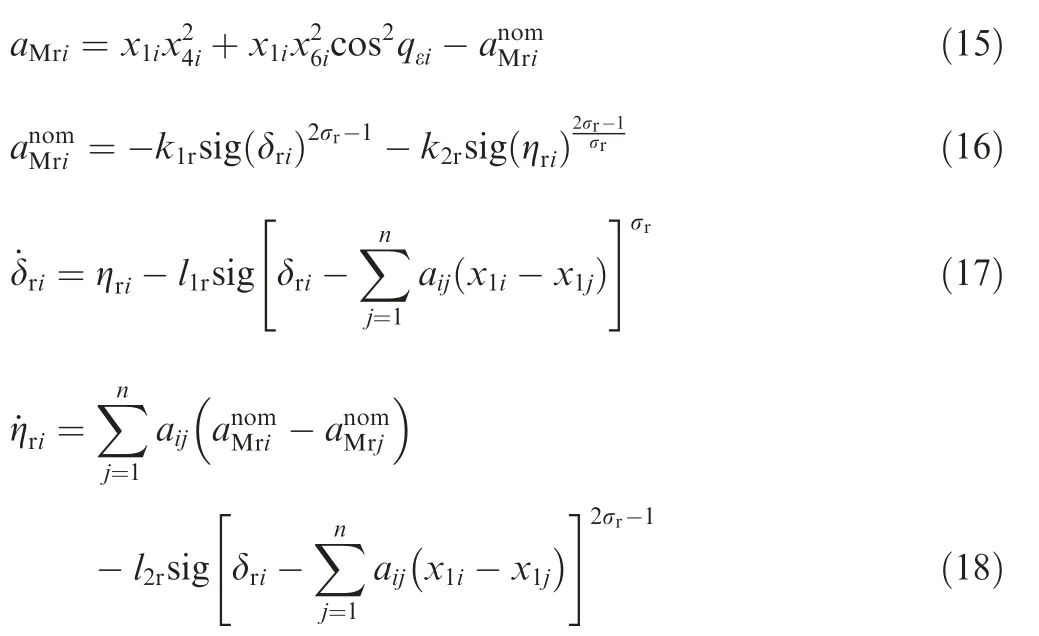
where l1r>0,l2r>0,k1r>0,k2r>0,0.5 <σr<1.
Proof.Definingand combining Eqs.(11),(15)-(18)yield the closed-loop guidance system in the direction of LOS
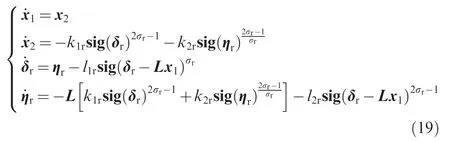
where L ∈Rn×nis Laplacian matrix of the graph G.
Define ex=δr-Lx1and ey=ηr-Lx2.From Eq.(19),there is

Considering system Eq.(20),in order to prove that exand eycan converge to zero in finite time,a Lyapunov function is chosen as follows:

As σr>0 and l2r>0,V1ris positive definite and radially unbounded.Taking time derivative of V1rand combining Eqs.(20)and(21)yield
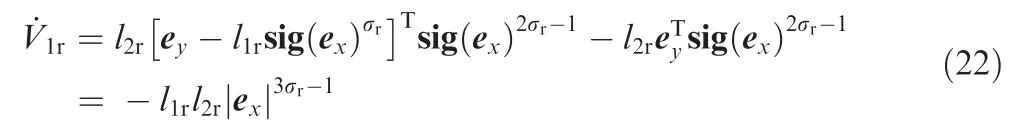
As l1r>0 and l2r>0,from Eq.(22)one can get ˙V1r≤0.When ˙V1r=0,there is ex=0.After that,from Eq.(20)one can get ey=0.Then,it follows from Lasalle's invariant set theorem that the equilibrium of the closed-loop system at the origin is globally asymptotically stable.Meanwhile,as the degree of homogeneous system Eq. (20) is κ=(σr-1)/σrand 0.5 <σr<1,one can get κ <0.Thus,it follows from homogeneous theory that the equilibrium of the system is finite time stable.That is,there exist δr=Lx1and ηr=Lx2after a finite time.Then,Eq.(19)can be rewritten as
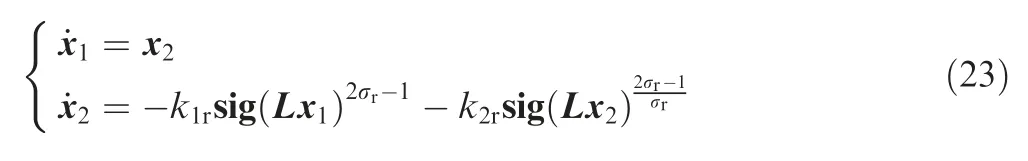
Define ωT=[ω1,ω2,...,ωn]∈R1×nwhich satisfies

Define

where

Then,combining Eqs.(23)and(26)yield
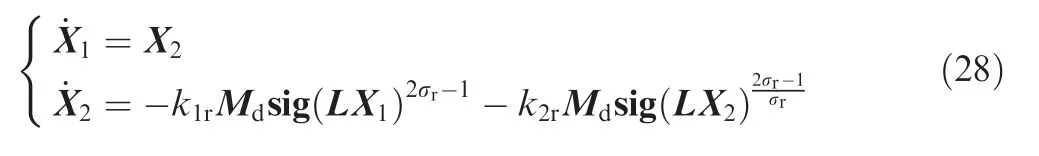
It can be seen from Eqs.(25)-(27)that x11=x12=...=x1nand x21=x22=...=x2ncan be achieved if and only if X1=0 and X2=0.Thus,the problem that the states x1iand x2iof system can achieve consensus in finite time respectively is transformed into the problem that the states X1and X2of system can converge to zero in finite time respectively.In order to prove it,a Lyapunov function candidate is chosen as
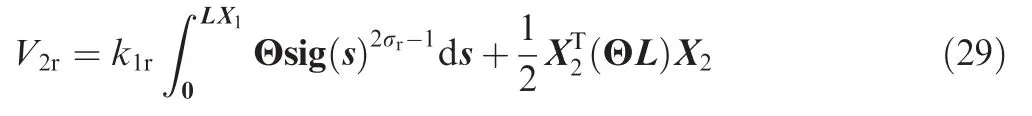
As LX1andhave the same sign componentwise,one hasfor anyFrom Lemma 1 it can be obtained that ΘL=(ΘL)T.Then,from Ref.19one hasfor anyTherefore,V2ris positive definite.
Considering L1=0 and combining Eqs.(24)and(27)yield

As LX2and sig(LX2)(2σr-1)/σrhave the same sign component-wise, combining Eqs. (29) and (30), the time derivative of V2rcan be obtained as
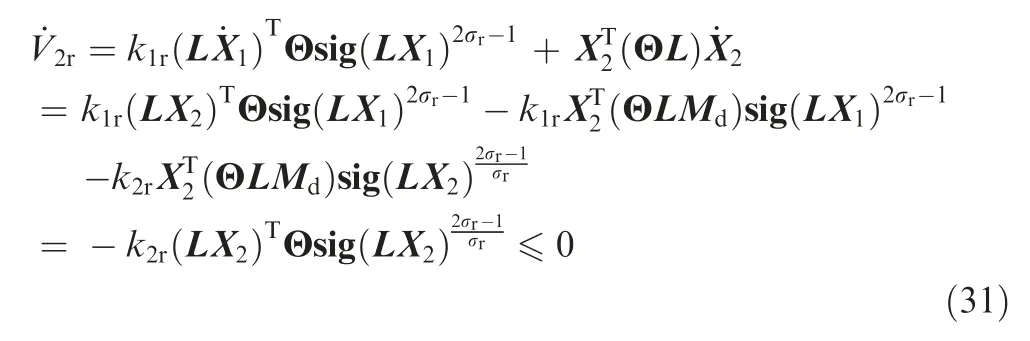
It follows from Eq. (31) that whenone has LX2=0.From Lemma 2 and L1=0,it can be obtained that LX2=0 is equal to

Combining Eqs.(25)and(27)yield

From Eqs.(26)and(33),one has

Substituting Eq.(32)into Eq.(34)and considering Eq.(25)yield

Substituting Eq.(35)into Eq.(32)yield X2=0.Thus,LX2=0 is equal to X2=0.In the same way,one can get LX1=0 is equal to X1=0.It can be seen from Eq.(31)that LX2=0 when=0,and then X2=0.From Eq.(28)one can get LX1=0 when=0,and then X1=0.Thus,one can obtain that X1=0 and X2=0 when=0.It follows from LaSalle's invariant set theorem that the equilibrium of the closed-loop system Eq.(28)at the origin is globally asymptotically stable.Meanwhile,through choosing the value of σr
among(0.5,1),one can make the degree κ=(σr-1)/σrof homogeneous system Eq.(28)be negative.Thus,it follows from Lemma 3 that the states X1and X2of the closed-loop system Eq.(28)can converge to zero in finite time.Then,it can be seen that the states x1iand x2iof system Eq.(19)can achieve consensus in finite time,respectively.The proof of Theorem 1 is completed.□
Remark 4.In Eq. (15), the first two terms are used to compensate for nonlinear characteristics of system,and the last term is used to achieve finite time consensus of the states x1iand x2iwithout measuring x2i.
3.2.Design of guidance law in elevation and azimuth direction of LOS
In this subsection,based on the homogeneous system theory13,22,25and sliding mode control theory,35-38two guidance laws aMεiand aMβiin the elevation and azimuth direction of LOS are derived respectively,which can ensure the fast finite-time convergence of the elevation and azimuth LOS angle as well as LOS angular rates without measurements of x2i.Thus,multiple missiles can attack moving target in desired elevation direction and azimuth direction of LOS.
From Eq.(10),the guidance model in the elevation direction of LOS can be expressed as follows:
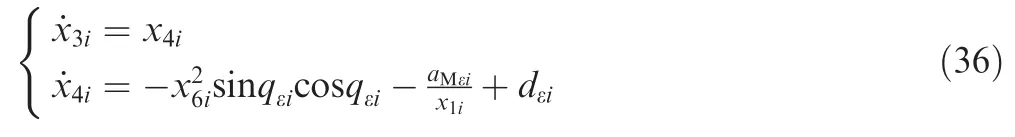
where dεi=-2x2ix4i/x1idenotes the disturbance term in the elevation direction of LOS.dε=[dε1,dε2,...,dεn]Trepresents the disturbance vector which consists of n missiles'dεi.
Similarly,from Eq.(10)the guidance model in the azimuth direction of LOS can be expressed as follows:
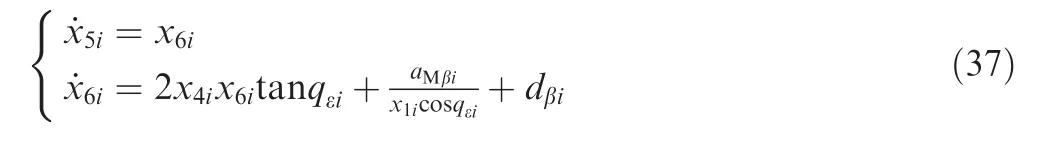
where dβi=-2x2ix6i/x1idenotes the disturbance term in the azimuth direction of LOS.dβ=[dβ1,dβ2,...,dβn]Trepresents the disturbance vector which consists of n missiles'dβi.
Based on the two guidance models given above,the corresponding two design objectives in this section are given as follows.The first objective is to develop the guidance law aMεiwhich can make x3iand x4iin Eq.(36)converge to zero in finite time without measuring x2i.That is,
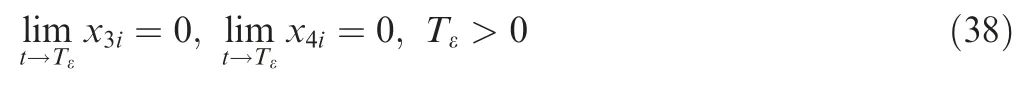
The second objective is to develop the guidance law aMβi,which can make x5iand x6iin Eq.(37)converge to zero in finite time without measuring x2i.That is,
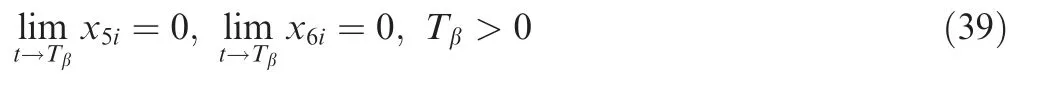
In order to design the guidance laws more conveniently,two assumptions are given as follows.
Assumption 5.There exists a constant lε>0 which can make
Assumption 6.There exists a constant lβ>0 which can make
To achieve the objective of Eq.(38),under Assumption 5,a novel guidance law in the elevation direction of LOS is presented with strict proof afterwards.
Theorem 2.Consider system Eq.(36),supposing Assumption 5 is satisfied,the guidance law in the elevation direction of LOS as is shown in Eqs.(40)-(42)can make x3iand x4iconverge to zero in finite time without measuring x2i.
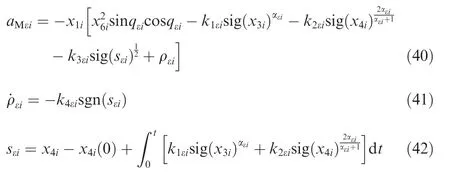
where k1εi>0,k2εi>0,k3εi>0,k4εi>lε,0 <αεi<1.
Proof.From Eq.(42),the time derivative of sεiis given by
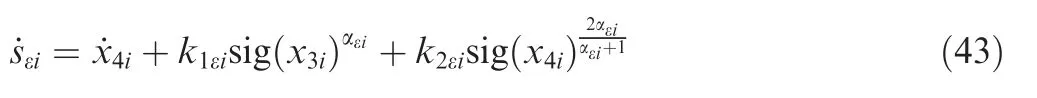
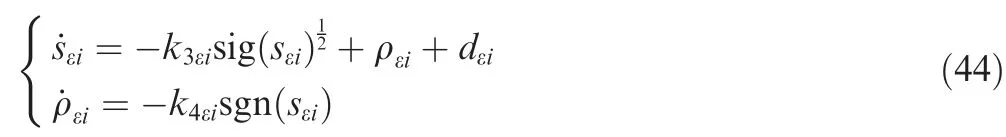
Then,combining Eqs.(36),(40),(41)and(43)yield
Defining

Then,Eq.(44)can be written as

In order to prove that sεican converge to zero in finite time,a Lyapunov function candidate is chosen as

where Pεi∈R2×2>0,ξεican be expressed as follows

Combining Eqs.(45),(46)and(48),the derivative of ξεiwith respect to time can be obtained as
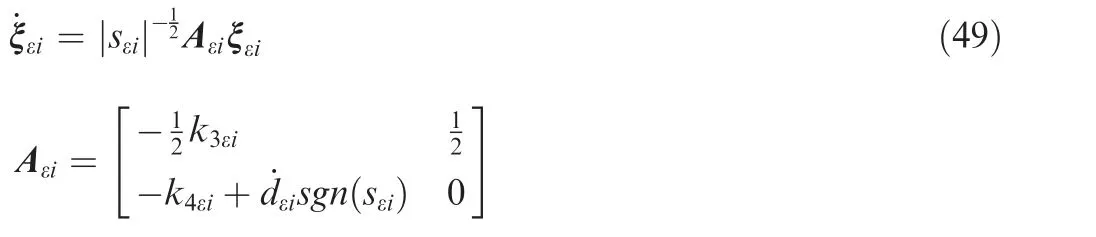
Taking the time derivative of Vεin Eq.(47)and substituting Eq.(49)into it yield
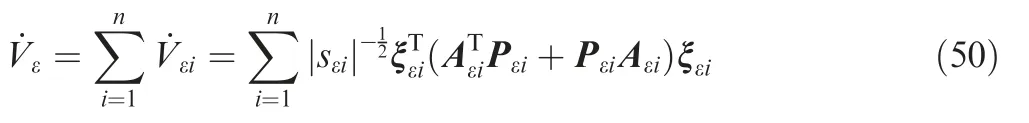
As k3εi>0 and k4εi>lε,all the eigenvalues of Aεihave negative real parts.Thus,it follows from linear time-invariant system's Lyapunov theorem that for any positive definite symmetric matrix Qεi,there exists a unique positive definite symmetric matrix Pεiwhich can make

Thus,by substituting Eq.(51)into Eq.(50),it can be seen that

Standard quadratic inequalities can be expressed as follows:
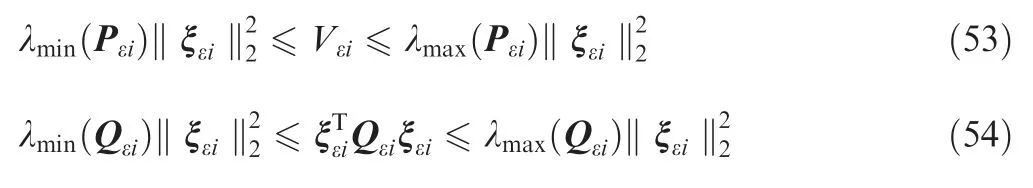
where λmin(·)and λmax(·)represent the minimum and maximum eigenvalue of the matrix,respectively.
Then,from Eqs.(53)and(54),it can be seen that

From Eqs.(48)and(53),it can be seen that
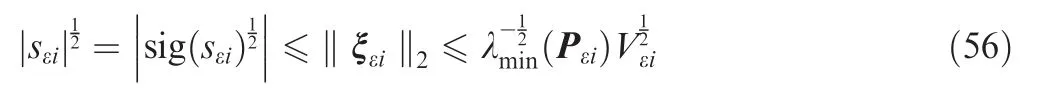
Combining Eqs.(52),(55)and(56)yield
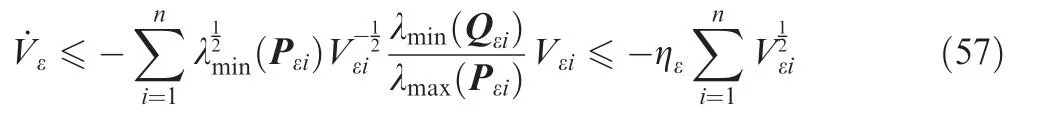

Thus,it follows from Eqs.(47)and(58)and Lemma 4 that all the missiles'ξεican converge to zero in finite time.That is,

It can be seen from Eqs.(48)and(59)that all the missiles'sεican converge to zero in finite time,that is

From Eq.(60),there is

Combining Eqs.(43)and(61)yield

Then,from Lemma 5 it can be seen that x3iand x4iof system Eq.(62)can converge to zero in finite time.Thus,under the guidance law proposed in Theorem 2,the states x3iand x4iof system Eq.(36)can converge to zero in finite time.The proof of Theorem 2 is completed.
To achieve the objective of Eq.(39),under Assumption 6,a novel guidance law in the azimuth direction of LOS is presented with strict proof afterwards.
Theorem 3.Consider system Eq.(37),supposing Assumption 6 is satisfied,the guidance law in the azimuth direction of LOS as is shown in Eqs.(63)-(65)can make x5iand x6iconverge to zero in finite time without measuring x2i.
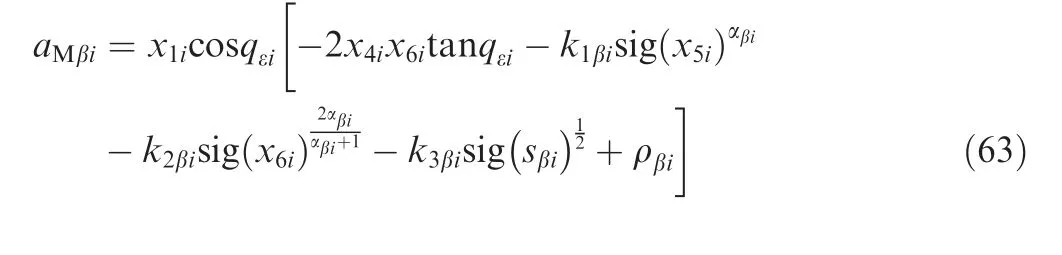
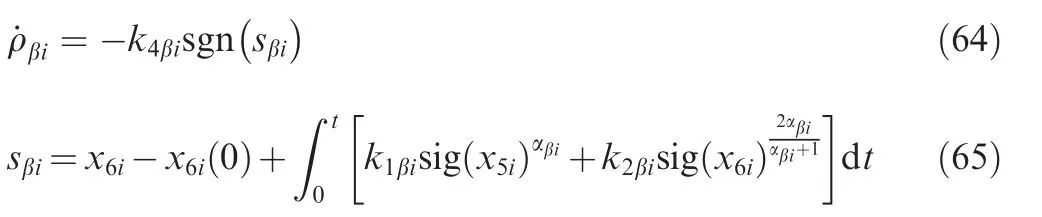
where k1βi>0,k2βi>0,k3βi>0,k4βi>lβ,0 <αβi<1.
Proof.As the proof process of Theorem 3 is similar with Theorem 2,it is omitted here.
Remark 5.No matter in Eq.(40)or Eq.(63),the first term in the square bracket is used to compensate for nonlinear characteristic of system,the second term and third term are used to make the states converge to zero in finite time,and the last two terms are used to offset the lumped disturbance without measuring x2i.
Remark 6.Although Theorems 1-3 have not given the formulas of convergence time upper bounds,it does not affect the use of guidance laws as the convergence times are always regulated to expected values through adjusting the parameters of the guidance laws.
4.Numerical simulation
In order to demonstrate the effectiveness of the proposed cooperative guidance law,numerical simulations are performed.Consider two cases that three missiles attack a stationary target and a moving target,respectively.In Case 1,the target is stationary.In Case 2,the target moves in a straight line with constant speed.The simulation step size is fixed and 5 ms.
The parameters of guidance law are selected as follows:k1r=5,k2r=5,l1r=6,l2r=6,σr=0.65.The parameters of guidance law are selected as follows: k1εi=2, k2εi=5,k3εi=5,k4εi=1,αεi=0.6,where i=1,2,3.The parameters of guidance law are selected as follows:k1βi=0.5,k2βi=2,k3βi=0.1,k4βi=0.1,αβi=0.8,where i=1,2,3.
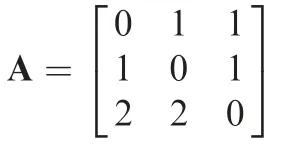
4.1.Case 1(stationary target)
In this case,the target is stationary,and the initial conditions of the target are shown in Table 2.The initial conditions of missiles are shown in Table 1.
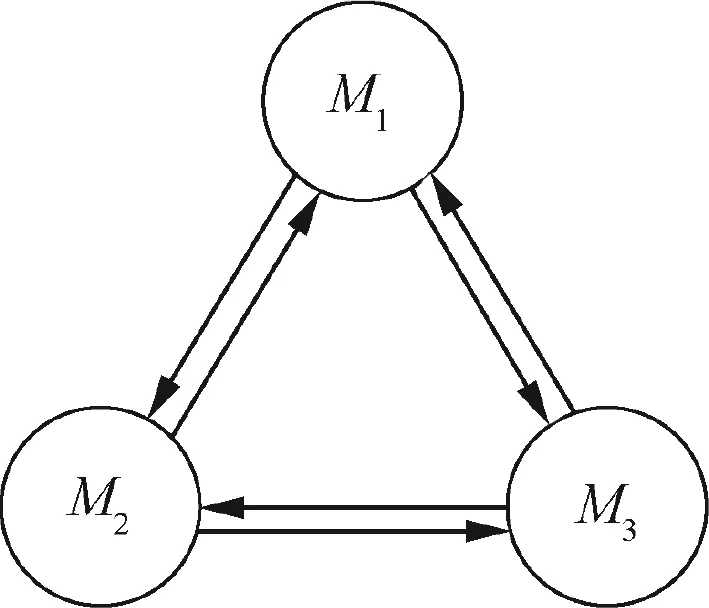
Fig.2 Communication topology for three missiles.

Table 1 Initial conditions of three missiles in Cases 1 and 2.

Table 2 Initial conditions of target in Case 1.
The simulation results are shown in Fig.3(a)-(i).Fig.3(a)indicates that all the three missiles can impact the moving target accurately.From Fig.3(b)-(d)it can be seen that under guidance law(15),all the three missiles'relative distances,radial velocities and times-to-go can achieve consensus after about 20 s.As shown in Fig.3(e),missiles'overload commands in LOS direction are smooth and within the reasonable bounds,which is beneficial to practical implementation.It is clear from Fig.3(f)and(g)that the LOS angles in the elevation direction and azimuth direction can converge to the desired values after about 5 s and 10 s,respectively,which means that under the proposed guidance laws(40)and(63),three missiles'LOS angles can converge to the desired values in finite time.It can be seen from Fig.3(h)and(i)that missiles'overload commands in elevation direction and azimuth direction of LOS are smooth and within the reasonable bounds,which is beneficial to practical implementation.What's more,the overload commands can converge to zero at the final time,which can help to improve the missiles'impact accuracy.The initial phase of the overload commands is large because of the large initial LOS angle errors.In spite of this,it is within the reasonable bounds and can make the LOS angles converge to the desired values as soon as possible.
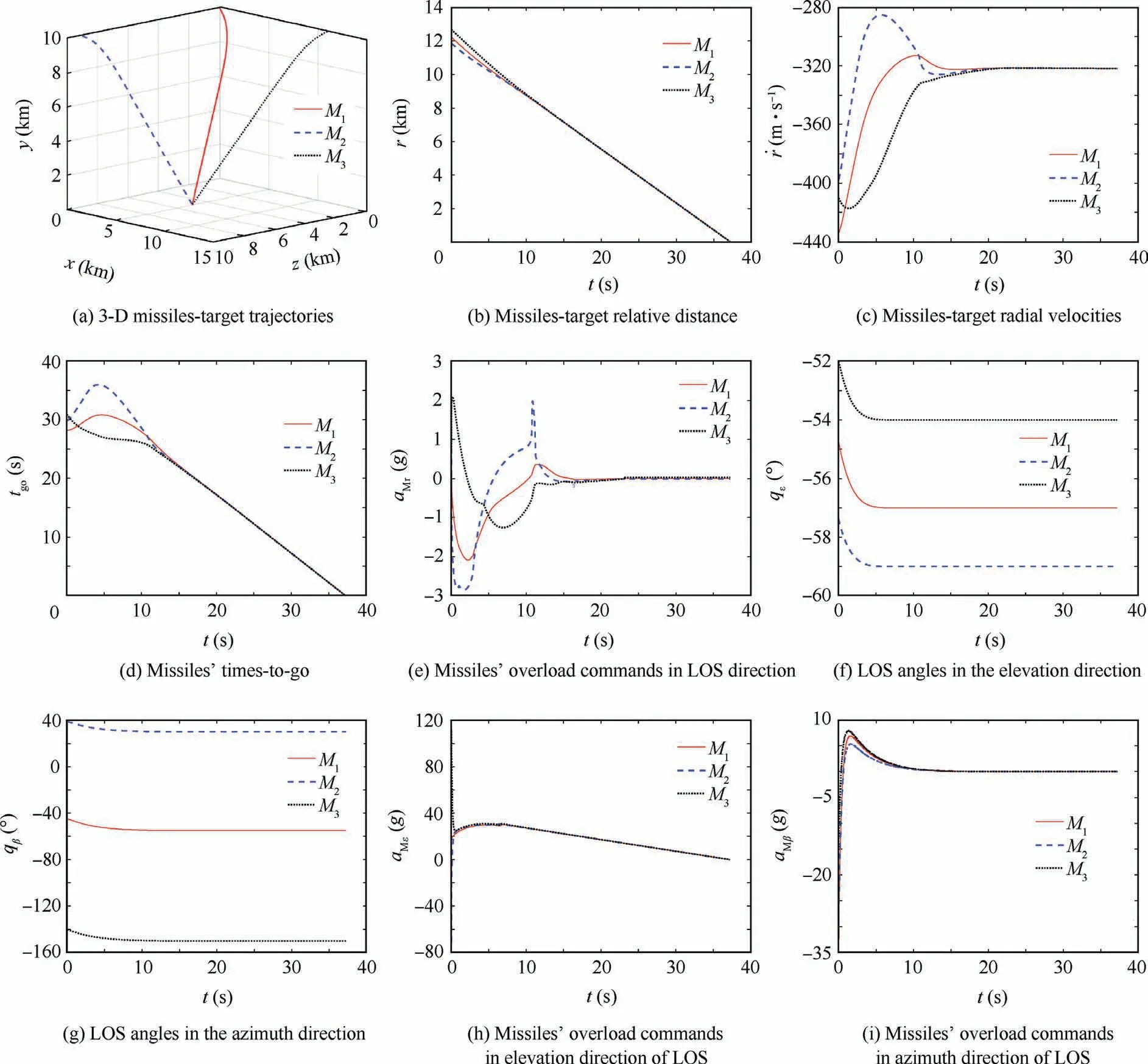
Fig.3 Simulation results of cooperative guidance in Case 1.
Three missiles'miss distances,impact times,elevation LOS angle errors and azimuth LOS angle errors are given in Table 3.All the missiles'miss distances are within 0.4 m,which means that the guidance law can make missiles hit the target directly.The impact times of all missiles are all the same,which means that all the missiles can hit the target simultaneously.Theelevation and azimuth LOS angle errors are within 0.00001°,which can meet practical requirement.

Table 3 Simulation results of cooperative guidance in Case 1.

Table 4 Initial conditions of target in Case 2.
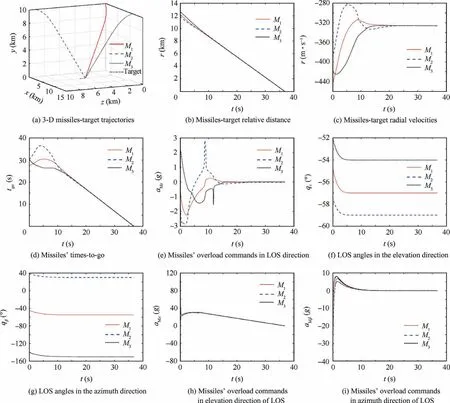
Fig.4 Simulation results of cooperative guidance in Case 2.

Table 5 Simulation results of cooperative guidance in Case 2.
4.2.Case 2(moving target with constant velocity)
In this case,the target is moving with constant velocity and the initial conditions of target are shown in Table 4.In order to show the robustness of the proposed guidance law,the initial conditions of missiles are the same as that in Case 1(see Table 1).
The simulation results are shown in Fig.4(a)-(i).Fig.4(a)indicates that all the three missiles can impact the moving target accurately.From Fig.4(b)-(d)it can be seen that under guidance law(15),all the three missiles'relative distances,radial velocities and times-to-go can achieve consensus after about 25 s.As shown in Fig.4(e),missiles'overload commands in LOS direction are smooth and within the reasonable bounds,which is beneficial to practical implementation.It is clear from Fig.4(f)and(g)that the LOS angles in the elevation direction and azimuth direction can converge to the desired values after about 5 s and 10 s,respectively,which means that under the proposed guidance laws(40)and(63),three missiles'LOS angles can converge to the desired values in finite time.It can be seen from Fig.4(h)and(i)that missiles'overload commands in elevation direction and azimuth direction of LOS are smooth and within the reasonable bounds,which is beneficial to practical implementation.What's more,the overload commands can converge to zero at the final time,which can help to improve the missiles'impact accuracy.The initial phase of the overload commands is large because of the large initial LOS angle errors.In spite of this,it is within the reasonable bounds and can make the LOS angles converge to the desired values as soon as possible.
Three missiles'miss distances,impact times,elevation LOS angle errors and azimuth LOS angle errors are given in Table 5.All the missiles'miss distances are within 1 m,which means that the guidance law can make missiles hit the target directly.The impact times of all missiles are all the same,which means that all the missiles can hit the target simultaneously.The elevation and azimuth LOS angle errors are within 0.0001°,which can meet practical requirement.
From the simulation results in Cases 1 and 2,it can be known that under the cooperative guidance law proposed in this paper,all the missiles can hit the target precisely and simultaneously, and the LOS angles can converge to the desired values in finite time,which demonstrates the effectiveness of the proposed guidance law.
5.Conclusions
In this paper,a novel 3-D cooperative guidance law without radial velocity measurements is proposed,which can be used to make multiple missiles impact target simultaneously with directed topologies and impact angle constraint.Firstly,a new guidance law in the LOS direction is designed,which can ensure multiple missiles'impact times reach consensus in finite time.Secondly,two guidance laws in elevation and azimuth direction of LOS are designed respectively,which can guarantee LOS angles converge to desired values and LOS angular rates converge to zero in finite time.Finally,simulation results are presented to show the effectiveness of the proposed cooperative guidance law.Future work will attempt to consider switching communication topologies and flight control dynamics in the design of cooperative guidance law for actual engagement missions.
Acknowledgements
This work was supported by the National Natural Science Foundation of China(Nos.61603114,61673135).
 CHINESE JOURNAL OF AERONAUTICS2019年5期
CHINESE JOURNAL OF AERONAUTICS2019年5期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Guide for Authors
- Effect of W addition on phase transformation and microstructure of powder metallurgic Ti-22Al-25Nb alloys during quenching and furnace cooling
- Thermoelastohydrodynamic analysis of misaligned bearings with texture on journal surface under high-speed and heavy-load conditions
- Role of the inter-pass cooling rate in recrystallization behaviors of Ni-based superalloy during interrupted hot compression
- Crystal orientation and morphology of α lamellae in wrought titanium alloys:On the role of microstructure evolution in β processing
- Data-driven model-free adaptive attitude control of partially constrained combined spacecraft with external disturbances and input saturation
